Grafų konvertavimo funkcijos ir grafikai. Elementariųjų funkcijų grafikų transformacija

Lygiagretus perdavimas.

VERTIMAS IŠ Y AŠIES

f(x) => f(x) - b
Tarkime, kad norite sukurti funkcijos y = f(x) - b grafiką. Nesunku pastebėti, kad šio grafiko ordinatės visoms x reikšmėms yra |b| vienetais mažiau už atitinkamas funkcijų grafiko y = f(x) ordinates b>0 ir |b| vienetų daugiau - ties b 0 arba aukštyn ties b Norėdami nubraižyti funkcijos y + b = f(x) grafiką, turėtumėte sudaryti funkcijos y = f(x) grafiką ir perkelti x ašį į |b| vienetų padidėjus b>0 arba |b| vienetų žemyn ties b

Perkelkite ABSCISS AŠĮ

f(x) => f(x + a)
Tarkime, kad norite nubraižyti funkciją y = f(x + a). Apsvarstykite funkciją y = f(x), kuri tam tikru momentu x = x1 įgyja reikšmę y1 = f(x1). Akivaizdu, kad funkcija y = f(x + a) įgis tokią pat reikšmę taške x2, kurio koordinatė nustatoma iš lygybės x2 + a = x1, t.y. x2 = x1 - a, o nagrinėjama lygybė galioja visų reikšmių visumai iš funkcijos apibrėžimo srities. Todėl funkcijos y = f(x + a) grafiką galima gauti lygiagrečiai perkeliant funkcijos y = f(x) grafiką išilgai x ašies į kairę |a| vienetų, kai a > 0 arba į dešinę po |a| a vienetai Norėdami sudaryti funkcijos y = f(x + a) grafiką, turėtumėte sudaryti funkcijos y = f(x) grafiką ir perkelti ordinačių ašį į |a| vienetų į dešinę, kai a>0 arba |a| vienetų į kairę ties a

Pavyzdžiai:

1.y=f(x+a)

2.y=f(x)+b

Atspindys.

FORMOS Y = F(-X) FUNKCIJOS GRAFIKOS KONSTRUKCIJA

f(x) => f(-x)
Akivaizdu, kad funkcijos y = f(-x) ir y = f(x) įgyja vienodas reikšmes taškuose, kurių abscisės yra lygios absoliučia verte, bet priešingos pagal ženklą. Kitaip tariant, funkcijos y = f(-x) grafiko ordinatės teigiamų (neigiamų) x reikšmių srityje bus lygios funkcijos y = f(x) grafiko ordinatėms. atitinkamoms neigiamoms (teigiamoms) x reikšmėms absoliučia verte. Taigi gauname tokią taisyklę.
Norėdami nubrėžti funkciją y = f(-x), turėtumėte nubraižyti funkciją y = f(x) ir atspindėti ją ordinatės atžvilgiu. Gautas grafikas yra funkcijos y = f(-x) grafikas

FORMOS Y = - F(X) FUNKCIJOS GRAFIKOS KONSTRUKCIJA

f(x) => - f(x)
Funkcijos y = - f(x) grafiko ordinatės visoms argumento reikšmėms yra lygios absoliučia reikšme, bet priešingos ženklu funkcijos y = f(x) grafiko ordinatėms. tos pačios argumento vertės. Taigi gauname tokią taisyklę.
Norėdami nubrėžti funkcijos y = - f(x) grafiką, turėtumėte nubraižyti funkcijos y = f(x) grafiką ir atspindėti jį x ašies atžvilgiu.

Pavyzdžiai:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Deformacija.

GRAFŲ DEFORMACIJA IŠ Y AŠIES

f(x) => k f(x)
Panagrinėkime y = k f(x) formos funkciją, kur k > 0. Nesunku pastebėti, kad esant vienodoms argumento reikšmėms, šios funkcijos grafiko ordinatės bus k kartų didesnės už funkcijos y = f(x) grafikas, kai k > 1 arba 1/k kartų mažesnis už funkcijos y = f(x) grafiko ordinates, kai k Sukurti funkcijos y = k grafiką f(x) ), turėtumėte sudaryti funkcijos y = f(x) grafiką ir jos ordinates padidinti k kartų, kai k > 1 (ištempti grafiką išilgai ordinačių ašies ) arba sumažinti jo ordinates 1/k kartų ties k
k > 1- driekiasi nuo Jaučio ašies
0 - suspaudimas prie OX ašies

GRAFIKOS DEFORMACIJA IEGAL ABSCISS AŠĮ

f(x) => f(k x)
Tegu reikia sudaryti funkcijos y = f(kx), kur k>0, grafiką. Apsvarstykite funkciją y = f(x), kuri savavališkame taške x = x1 įgyja reikšmę y1 = f(x1). Akivaizdu, kad funkcija y = f(kx) įgauna tą pačią reikšmę taške x = x2, kurio koordinatę lemia lygybė x1 = kx2, ir ši lygybė galioja visų reikšmių visumai. x iš funkcijos apibrėžimo srities. Vadinasi, funkcijos y = f(kx) grafikas pasirodo suspaustas (jei k 1) išilgai abscisių ašies funkcijos y = f(x) grafiko atžvilgiu. Taigi mes gauname taisyklę.
Norėdami sukurti funkcijos y = f(kx) grafiką, turėtumėte sudaryti funkcijos y = f(x) grafiką ir sumažinti jos abscises k kartų, kai k>1 (suspausti grafiką išilgai abscisių ašies) arba padidinti jo abscisės 1/k kartų k
k > 1- suspaudimas iki Oy ašies
0 - tempimas nuo OY ašies

Darbus atliko Aleksandras Čičkanovas, Dmitrijus Leonovas, vadovaujami T. V. Tkacho, S. M. Vyazovo, I. V. Ostroverkhova.
©2014 m

Darbo tekstas skelbiamas be vaizdų ir formulių.
Pilna versija darbą galima rasti skirtuke „Darbo failai“ PDF formatu

Įvadas

Funkcijų grafikų transformavimas yra viena iš pagrindinių matematinių sąvokų, tiesiogiai susijusių su praktinė veikla. Su funkcijų grafikų transformacija pirmą kartą susiduriama 9 klasės algebroje, studijuojant temą „Kvadratinė funkcija“. Kvadratinė funkcija pristatoma ir tiriama glaudžiai susijusi su kvadratines lygtis ir nelygybės. Taip pat aptariama daug matematinių sąvokų grafiniai metodai Pavyzdžiui, 10-11 klasėse funkcijos tyrimas leidžia rasti apibrėžimo sritį ir funkcijos vertės sritį, mažėjimo ar didėjimo sritis, asimptotes, pastovaus ženklo intervalus ir kt. klausimas taip pat iškeltas GIA. Iš to seka, kad funkcijų grafikų sudarymas ir transformavimas yra vienas pagrindinių matematikos mokymo mokykloje uždavinių.

Tačiau norėdami braižyti daugelio funkcijų grafikus, galite naudoti daugybę metodų, kurie palengvina braižymą. Tai, kas išdėstyta aukščiau, lemia aktualumą tyrimų temomis.

Tyrimo objektas yra studijuoti grafikų transformaciją mokyklinėje matematikoje.

Studijų dalykas - funkcijų grafikų konstravimo ir transformavimo procesas vidurinėje mokykloje.

Probleminis klausimas: Ar įmanoma sukurti nepažįstamos funkcijos grafiką, jei turite įgūdžių konvertuoti grafikus? elementarios funkcijos?

Tikslas: funkcijų braižymas nepažįstamoje situacijoje.

Užduotys:

1. Išanalizuoti mokomąją medžiagą apie nagrinėjamą problemą. 2. Nustatyti funkcijų grafikų transformavimo schemas mokykliniame matematikos kurse. 3. Pasirinkite daugiausiai veiksmingi metodai ir funkcijų grafikų konstravimo ir transformavimo įrankiai. 4. Gebėti taikyti šią teoriją sprendžiant problemas.

Reikalingos pradinės žinios, įgūdžiai ir gebėjimai:

Funkcijos reikšmę nustatykite pagal jos argumento reikšmę kada įvairiais būdais funkcijų priskyrimas;

Sudaryti tiriamų funkcijų grafikus;

Apibūdinkite funkcijų elgseną ir savybes naudodami grafiką, o paprasčiausiais atvejais naudodami formulę; iš funkcijos grafiko raskite didžiausias ir mažiausias reikšmes;

Aprašymai naudojant įvairių priklausomybių funkcijas, jas atvaizduojant grafiškai, interpretuojant grafikus.

Pagrindinė dalis

Teorinė dalis

Kaip pradinį funkcijos y = f(x) grafiką pasirinksiu kvadratinę funkciją y = x 2 . Išnagrinėsiu šio grafiko transformacijos atvejus, susijusius su šią funkciją apibrėžiančios formulės pokyčiais ir padarysiu išvadas dėl bet kurios funkcijos.

1. Funkcija y = f(x) + a

Naujoje formulėje funkcijų reikšmės (grafiko taškų ordinatės) keičiasi skaičiumi a, lyginant su „senąja“ funkcijos reikšme. Dėl to funkcijos grafikas perkeliamas lygiagrečiai išilgai OY ašies:

aukštyn, jei a > 0; žemyn, jei a< 0.

IŠVADA

Taigi funkcijos y=f(x)+a grafikas gaunamas iš funkcijos y=f(x) grafiko, naudojant lygiagretų vertimą išilgai ordinačių ašies vienetais aukštyn, jei a > 0, ir vienetais žemyn. jeigu< 0.

2. Funkcija y = f(x-a),

Naujoje formulėje argumentų reikšmės (grafiko taškų abscisės) keičiasi skaičiumi a, palyginti su „senąja“ argumento reikšme. Dėl to funkcijos grafikas perkeliamas lygiagrečiai išilgai OX ašies: į dešinę, jei a< 0, влево, если a >0.

IŠVADA

Tai reiškia, kad funkcijos y= f(x - a) grafikas gaunamas iš funkcijos y=f(x) grafiko lygiagrečiai perkeliant išilgai abscisių ašies vienetais į kairę, jei a > 0, ir a vienetai į dešinę, jei a< 0.

3. Funkcija y = k f(x), kur k > 0 ir k ≠ 1

Naujoje formulėje funkcijų reikšmės (grafiko taškų ordinatės) keičiasi k kartų, palyginti su „senąja“ funkcijos reikšme. Tai lemia: 1) „ištempimą“ nuo taško (0; 0) išilgai OY ašies koeficientu k, jei k > 1, 2) „suspaudimą“ iki taško (0; 0) išilgai OY ašies koeficientas, jei 0< k < 1.

IŠVADA

Vadinasi: norint sukurti funkcijos y = kf(x), kur k > 0 ir k ≠ 1, grafiką, reikia funkcijos y = f(x) pateikto grafiko taškų ordinates padauginti iš k. Tokia transformacija vadinama tempimu iš taško (0; 0) išilgai OY ašies k kartų, jei k > 1; suspaudimas iki taško (0; 0) išilgai OY ašies kartų, jei 0< k < 1.

4. Funkcija y = f(kx), kur k > 0 ir k ≠ 1

Naujoje formulėje argumentų reikšmės (grafiko taškų abscisės) keičiasi k kartų, palyginti su „senąja“ argumento reikšme. Tai lemia: 1) „ištempimą“ nuo taško (0; 0) išilgai OX ašies 1/k kartų, jei 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

IŠVADA

Ir taip: norint sudaryti funkcijos y = f(kx), kur k > 0 ir k ≠ 1, grafiką, reikia padauginti funkcijos y=f(x) pateikto grafiko taškų abscises iš k . Tokia transformacija vadinama tempimu iš taško (0; 0) išilgai OX ašies 1/k kartų, jei 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. Funkcija y = - f (x).

Šioje formulėje funkcijų reikšmės (grafiko taškų ordinatės) yra apverstos. Dėl šio pakeitimo pradinis funkcijos grafikas rodomas simetriškai Ox ašies atžvilgiu.

IŠVADA

Norint nubraižyti funkcijos y = - f (x) grafiką, reikia funkcijos y= f(x) grafiko.

simetriškai atspindi OX ašį. Ši transformacija vadinama simetrijos transformacija apie OX ašį.

6. Funkcija y = f (-x).

Šioje formulėje argumento reikšmės (grafiko taškų abscisės) yra apverstos. Dėl šio pakeitimo pradinis funkcijos grafikas OY ašies atžvilgiu rodomas simetriškai.

Funkcijos y = - x² pavyzdys ši transformacija nepastebima, nes ši funkcija yra lygi ir grafikas po transformacijos nesikeičia. Ši transformacija matoma, kai funkcija nelyginė ir kai ji nėra nei lyginė, nei nelyginė.

7. Funkcija y = |f(x)|.

Naujoje formulėje funkcijų reikšmės (grafiko taškų ordinatės) yra po modulio ženklu. Dėl to pradinės funkcijos grafiko dalys su neigiamomis ordinatėmis išnyksta (t. y. tos, kurios yra apatinėje pusiau plokštumoje Ox ašies atžvilgiu) ir simetriškas šių dalių rodymas Ox ašies atžvilgiu.

8. Funkcija y= f (|x|).

Naujoje formulėje argumentų reikšmės (grafiko taškų abscisės) yra po modulio ženklu. Dėl to pradinės funkcijos grafiko dalys su neigiamomis abscisėmis išnyksta (t. y. esančios kairėje pusplokštumoje OY ašies atžvilgiu) ir jos pakeičiamos pradinio grafiko dalimis, kurios yra simetriškos OY ašies atžvilgiu. .

Praktinė dalis

Pažvelkime į keletą aukščiau pateiktos teorijos taikymo pavyzdžių.

1 PAVYZDYS.

Sprendimas. Transformuokime šią formulę:

1) Sukurkime funkcijos grafiką

2 PAVYZDYS.

Nubraižykite formule pateiktą funkciją

Sprendimas. Pakeiskime šią formulę paryškindami ją kvadratinis trinaris dvinario kvadratas:

1) Sukurkime funkcijos grafiką

2) Atlikite lygiagretų sudaryto grafiko perkėlimą į vektorių

3 PAVYZDYS.

UŽDUOTIS IŠ vieningo valstybinio egzamino Padalinės funkcijos grafikas

Funkcijos grafikas Funkcijos y=|2(x-3)2-2| grafikas; 1

Pagrindinės elementarios funkcijos gryna forma be transformacijos yra retos, todėl dažniausiai tenka dirbti su elementariomis funkcijomis, kurios buvo gautos iš pagrindinių pridedant konstantas ir koeficientus. Tokie grafikai konstruojami naudojant duotų elementariųjų funkcijų geometrines transformacijas.

Pažiūrėkime į pavyzdį kvadratinė funkcija formos y = - 1 3 x + 2 3 2 + 2, kurios grafikas yra parabolė y = x 2, kuri suspausta tris kartus O y atžvilgiu ir simetriška O x atžvilgiu ir paslinkta 2 3 išilgai O x į dešinę, 2 vienetais išilgai O u aukštyn. Koordinačių tiesėje tai atrodo taip:

Yandex.RTB R-A-339285-1

Funkcijos grafiko geometrinės transformacijos

Taikant duoto grafiko geometrines transformacijas, gauname, kad grafikas pavaizduotas ± k 1 · f (± k 2 · (x + a)) + b formos funkcija, kai k 1 > 0, k 2 > 0 suspaudimo koeficientai yra 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 išilgai O y ir O x. Ženklas prieš koeficientus k 1 ir k 2 rodo simetrišką grafiko atvaizdavimą ašių atžvilgiu, a ir b perkelia jį išilgai O x ir išilgai O y.

1 apibrėžimas

Yra 3 tipai geometrinės grafiko transformacijos:

• Mastelio keitimas palei O x ir O y. Tam įtakos turi koeficientai k 1 ir k 2, jei jie nėra lygūs 1, kai yra 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, tada grafikas ištempiamas išilgai O y ir suspaudžiamas išilgai O x.
• Simetrinis rodymas koordinačių ašių atžvilgiu. Jei prieš k 1 yra ženklas „-“, simetrija yra O x atžvilgiu, o prieš k 2 – O y atžvilgiu. Jei trūksta „-“, tada sprendžiant elementas praleidžiamas;
• Lygiagretus perkėlimas (pamaina) palei O x ir O y. Transformacija atliekama, jei koeficientai a ir b nelygūs 0. Jei a yra teigiamas, grafikas pasislenka į kairę | a | vienetų, jei a yra neigiamas, tada į dešinę tuo pačiu atstumu. B reikšmė lemia judėjimą išilgai O y ašies, o tai reiškia, kad kai b teigiama, funkcija juda aukštyn, o kai b neigiama – žemyn.

Pažvelkime į sprendimus naudodami pavyzdžius, pradedant nuo galios funkcija.

1 pavyzdys

Transformuokite y = x 2 3 ir nubraižykite funkciją y = - 1 2 · 8 x - 4 2 3 + 3 .

Sprendimas

Pavaizduokime funkcijas taip:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Kur k 1 = 2, verta atkreipti dėmesį į „-“, a = - 1 2, b = 3. Iš čia gauname, kad geometrinės transformacijos atliekamos ištempiant išilgai O y du kartus, rodomos simetriškai O x atžvilgiu, paslinkus į dešinę 1 2 ir į viršų 3 vienetais.

Jei pavaizduotume pradinę galios funkciją, tai gausime

du kartus ištempus išilgai O y turime tą

Atvaizdavimas, simetriškas O x atžvilgiu, turi formą

ir pasukite į dešinę 1 2

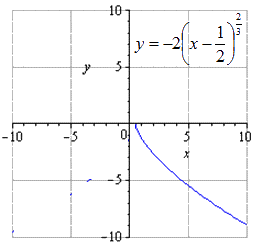
atrodo 3 vienetų judėjimas aukštyn

Pažvelkime į eksponentinių funkcijų transformacijas naudodami pavyzdžius.

2 pavyzdys

Sudarykite eksponentinės funkcijos y = - 1 2 1 2 (2 - x) + 8 grafiką.

Sprendimas.

Transformuokime funkciją pagal laipsnio funkcijos savybes. Tada mes tai gauname

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Iš to matome, kad gauname transformacijų grandinę y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Mes matome, kad originalas eksponentinė funkcija atrodo kaip

Suspaudus du kartus palei O y duoda

Ištempimas palei O x

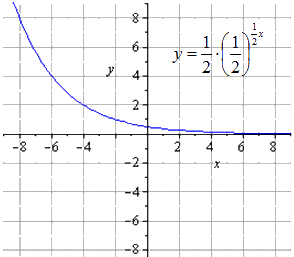
Simetrinis atvaizdavimas O x atžvilgiu

Atvaizdavimas yra simetriškas O y atžvilgiu

Pakilkite 8 vienetais aukštyn

Pažvelkime į sprendimą naudodami pavyzdį logaritminė funkcija y = log(x) .

3 pavyzdys

Sukurkite funkciją y = ln e 2 · - 1 2 x 3 naudodami transformaciją y = ln (x) .

Sprendimas

Norint išspręsti, reikia naudoti logaritmo savybes, tada gauname:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Logaritminės funkcijos transformacijos atrodo taip:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Nubraižykime pradinę logaritminę funkciją

Suspaudžiame sistemą pagal O y

Ištempiame išilgai O x

Atliekame kartografavimą O y atžvilgiu

Mes pasislenkame 2 vienetais, gauname

Norėdami konvertuoti grafikus trigonometrinė funkcija reikia pritaikyti ± k 1 · f (± k 2 · (x + a)) + b formos sprendimo schemą. Būtina, kad k 2 būtų lygus T k 2 . Iš čia gauname 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Pažvelkime į uždavinių sprendimo pavyzdžius su transformacijomis y = sin x.

4 pavyzdys

Sukurkite y = - 3 sin 1 2 x - 3 2 - 2 grafiką naudodami funkcijos y=sinx transformacijas.

Sprendimas

Funkciją reikia sumažinti iki formos ± k 1 · f ± k 2 · x + a + b. Už tai:

y = - 3 nuodėmė 1 2 x - 3 2 - 2 = - 3 nuodėmė 1 2 (x - 3) - 2

Matyti, kad k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Kadangi prieš k 1 yra „-“, bet ne prieš k 2, tada gauname formos transformacijų grandinę:

y = nuodėmė (x) → y = 3 nuodėmė (x) → y = 3 nuodėmė 1 2 x → y = - 3 nuodėmė 1 2 x → → y = - 3 nuodėmė 1 2 x - 3 → y = - 3 nuodėmė 1 2 (x - 3) - 2

Detali sinusinės bangos transformacija. Nubraižydami pradinę sinusoidę y = sin (x), matome, kad mažiausias teigiamas periodas laikomas T = 2 π. Maksimumo radimas taškuose π 2 + 2 π · k; 1, o mažiausias - - π 2 + 2 π · k; - 1, k ∈ Z.

O y ištemptas tris kartus, vadinasi, svyravimų amplitudės padidėjimas padidės 3 kartus. T = 2 π yra mažiausias teigiamas periodas. Maksimumai eina į π 2 + 2 π · k; 3, k ∈ Z, minimumai - - π 2 + 2 π · k; - 3, k ∈ Z.

Ištempę išilgai O x per pusę, matome, kad mažiausias teigiamas periodas padidėja 2 kartus ir yra lygus T = 2 π k 2 = 4 π. Maksimumai eina į π + 4 π · k; 3, k ∈ Z, minimumai – in - π + 4 π · k; - 3, k ∈ Z.

Vaizdas sukuriamas simetriškai O x atžvilgiu. Mažiausias teigiamas periodas šiuo atveju nekinta ir yra lygus T = 2 π k 2 = 4 π. Maksimalus perėjimas atrodo taip - π + 4 π · k; 3, k ∈ Z, o minimumas yra π + 4 π · k; - 3, k ∈ Z.

Grafikas paslinktas žemyn 2 vienetais. Minimalus bendras laikotarpis nesikeičia. Rasti maksimumus su perėjimu į taškus - π + 3 + 4 π · k; 1, k ∈ Z, minimumai - π + 3 + 4 π · k; -5, k ∈ Z.

Įjungta šioje stadijoje trigonometrinės funkcijos grafikas laikomas transformuotu.

Panagrinėkime detalią funkcijos y = cos x transformaciją.

5 pavyzdys

Sukurkite funkcijos y = 3 2 cos 2 - 2 x + 1 grafiką, naudodami funkcijos transformaciją formos y = cos x.

Sprendimas

Pagal algoritmą duotąją funkciją reikia redukuoti iki formos ± k 1 · f ± k 2 · x + a + b. Tada mes tai gauname

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Iš sąlygos aišku, kad k 1 = 3 2, k 2 = 2, a = - 1, b = 1, kur k 2 turi „-“, bet prieš k 1 jo nėra.

Iš to matome, kad gauname formos trigonometrinės funkcijos grafiką:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1

Žingsnis po žingsnio kosinuso transformacija su grafine iliustracija.

Atsižvelgiant į grafiką y = cos(x), aišku, kad trumpiausias bendras periodas yra T = 2π. 2 π · k maksimumų radimas; 1, k ∈ Z, ir yra π + 2 π · k minimumai; - 1, k ∈ Z.

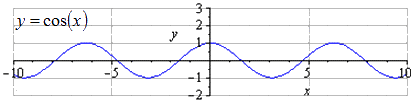
Ištempus išilgai Oy 3 2 kartus, svyravimų amplitudė padidėja 3 2 kartus. T = 2 π yra mažiausias teigiamas periodas. 2 π · k maksimumų radimas; 3 2, k ∈ Z, minimumai π + 2 π · k; - 3 2 , k ∈ Z .

Suspaudę išilgai O x per pusę, matome, kad mažiausias teigiamas periodas yra skaičius T = 2 π k 2 = π. Įvyksta maksimumų perėjimas į π · k; 3 2 , k ∈ Z , minimumai - π 2 + π · k ; - 3 2 , k ∈ Z .

Simetrinis kartografavimas Oy atžvilgiu. Kadangi grafikas yra nelyginis, jis nepasikeis.

Kai grafikas pasislenka 1 . Mažiausiu teigiamu periodu T = π pokyčių nėra. π · k + 1 maksimumų radimas; 3 2, k ∈ Z, minimumai - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Paslinkus 1, mažiausias teigiamas periodas yra lygus T = π ir nesikeičia. π · k + 1 maksimumų radimas; 5 2, k ∈ Z, minimumai π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Kosinuso funkcijos transformacija baigta.

Panagrinėkime transformacijas naudodami pavyzdį y = t g x.

6 pavyzdys

Sukurkite funkcijos y = - 1 2 t g π 3 - 2 3 x + π 3 grafiką, naudodami funkcijos y = t g (x) transformacijas.

Sprendimas

Pirmiausia reikia sumažinti pateiktą funkciją iki formos ± k 1 · f ± k 2 · x + a + b, po to gauname, kad

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Aiškiai matyti, kad k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, o prieš koeficientus k 1 ir k 2 yra „-“. Tai reiškia, kad transformavus tangentoidus gauname

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Žingsnis po žingsnio liestinių transformacija su grafiniu vaizdu.

Turime, kad pradinis grafikas yra y = t g (x) . Teigiamo periodo pokytis lygus T = π. Apibrėžimo sritis laikoma - π 2 + π · k ; π 2 + π · k, k ∈ Z.

Suspaudžiame 2 kartus išilgai Oy. T = π laikomas mažiausiu teigiamu periodu, kur apibrėžimo sritis turi formą - π 2 + π · k; π 2 + π · k, k ∈ Z.

Ištempkite išilgai O x 3 2 kartus. Apskaičiuokime mažiausią teigiamą periodą, kuris buvo lygus T = π k 2 = 3 2 π . O funkcijos su koordinatėmis apibrėžimo sritis yra 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, keičiasi tik apibrėžimo sritis.

Simetrija vyksta O x pusėje. Šiuo metu laikotarpis nesikeis.

Būtina simetriškai rodyti koordinačių ašis. Šiuo atveju apibrėžimo sritis nesikeičia. Tvarkaraštis sutampa su ankstesniu. Tai rodo, kad liestinės funkcija yra nelyginė. Jei reikia nelyginė funkcija nustatykite simetrišką O x ir O y atvaizdavimą, tada transformuokite į pradinę funkciją.

Priklausomai nuo fizinių procesų sąlygų, kai kurie dydžiai įgyja pastovias reikšmes ir vadinami konstantomis, kiti tam tikromis sąlygomis keičiasi ir vadinami kintamaisiais.

Kruopštus tyrimas aplinką tai rodo fiziniai dydžiai priklausomi vienas nuo kito, tai yra, pasikeitus kai kuriems kiekiams, pasikeičia ir kiti.

Matematinė analizė tiria kiekybinius ryšius tarp tarpusavyje kintančių dydžių, abstrahuojantis nuo konkrečios fizinės reikšmės. Viena iš pagrindinių matematinės analizės sąvokų yra funkcijos sąvoka.

Apsvarstykite rinkinio elementus ir rinkinio elementus
(3.1 pav.).

Jeigu tarp aibių elementų nustatoma tam tikra atitiktis
Ir taisyklės pavidalu , tada jie pažymi, kad funkcija yra apibrėžta
.

Apibrėžimas 3.1. Susirašinėjimas , kuris susieja su kiekvienu elementu ne tuščias rinkinys
tam tikras gerai apibrėžtas elementas ne tuščias rinkinys , vadinamas funkcija arba atvaizdavimu
V .

Simboliškai rodomas
V parašyta taip:

.

Tuo pačiu metu daugelis
vadinamas funkcijos apibrėžimo sritimi ir žymimas
.

Savo ruožtu daugelis vadinamas funkcijos reikšmių diapazonu ir žymimas
.

Be to, reikia pažymėti, kad rinkinio elementai
vadinami nepriklausomais kintamaisiais, aibės elementais vadinami priklausomais kintamaisiais.

Funkcijos nustatymo metodai

Funkciją galima nurodyti šiais pagrindiniais būdais: lenteliniu, grafiniu, analitiniu.

Jei remiantis eksperimentiniais duomenimis sudaromos lentelės, kuriose yra funkcijos reikšmės ir atitinkamos argumentų reikšmės, tada šis funkcijos nurodymo būdas vadinamas lentele.

Tuo pačiu, jei kai kurie eksperimento rezultato tyrimai rodomi registratoriuje (osciloskopas, registratorius ir pan.), tada pažymima, kad funkcija nurodoma grafiškai.

Labiausiai paplitęs yra analitinis funkcijos nurodymo būdas, t.y. metodas, kai nepriklausomas ir priklausomas kintamasis susiejamas naudojant formulę. Šiuo atveju svarbų vaidmenį atlieka funkcijos apibrėžimo sritis:

skirtingi, nors juos suteikia tie patys analitiniai ryšiai.

Jei nurodysite tik funkcijos formulę
, tada manome, kad šios funkcijos apibrėžimo sritis sutampa su tų kintamojo reikšmių rinkiniu , kurio išraiška
turi prasmę. Šiuo atžvilgiu ypatingas vaidmuo tenka funkcijos apibrėžimo srities suradimo problemai.

Užduotis 3.1. Raskite funkcijos sritį

Sprendimas

Pirmasis terminas įgauna tikrąsias reikšmes, kai
, o antrasis - val. Taigi, norint rasti tam tikros funkcijos apibrėžimo sritį, būtina išspręsti nelygybių sistemą:

Dėl to gaunamas tokios sistemos sprendimas. Todėl funkcijos apibrėžimo sritis yra segmentas
.

Paprasčiausios funkcijų grafikų transformacijos

Funkcijų grafikų sudarymas gali būti žymiai supaprastintas, jei naudosite gerai žinomus pagrindinių elementariųjų funkcijų grafikus. Šios funkcijos vadinamos pagrindinėmis elementariomis funkcijomis:

1) galios funkcija
Kur
;

2) eksponentinė funkcija
Kur
Ir
;

3) logaritminė funkcija
, Kur - bet koks teigiamas skaičius, skiriasi nuo vienybės:
Ir
;

4) trigonometrinės funkcijos




;
.

5) atvirkštinės trigonometrinės funkcijos
;
;
;
.

Elementariosios funkcijos yra funkcijos, gaunamos iš pagrindinių elementariųjų funkcijų naudojant keturias aritmetines operacijas ir superpozicijas, taikomas baigtinį skaičių kartų.

Paprastos geometrinės transformacijos taip pat leidžia supaprastinti funkcijų grafiko sudarymo procesą. Šios transformacijos pagrįstos šiais teiginiais:

Funkcijos y=f(x+a) grafikas yra grafikas y=f(x), paslinktas (>0 į kairę,< 0 вправо) на |a| единиц параллельно осиOx.

Funkcijos y=f(x) +b grafikas yra y=f(x) grafikas, paslinktas (b>0 aukštyn, b< 0 вниз) на |b| единиц параллельно осиOy.

Funkcijos y = mf(x) (m0) grafikas yra y = f(x) grafikas, ištemptas (kai m>1) m kartų arba suspaustas (esant 0

Funkcijos y = f(kx) grafikas yra y = f(x) grafikas, suspaustas (kai k >1) k kartų arba ištemptas (jeigu 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.