Žvaigždžių naujienos
Iracionalių trigonometrinių nelygybių sprendimas. Paprastų trigonometrinių nelygybių sprendimo algoritmas ir trigonometrinių nelygybių sprendimo metodų atpažinimas
Baltarusijos Respublikos švietimo ministerija
Švietimo įstaiga
„Gomelio valstybinis universitetas
pavadintas Francysko Skarynos vardu
Matematikos fakultetas
Algebros ir geometrijos katedra
Priimta gynybai
Galva Skyrius Shemetkov L.A.
Trigonometrinės lygtys ir nelygybės
Kursinis darbas
Vykdytojas:
M-51 grupės mokinys
CM. Gorskis
Mokslinis vadovas Ph.D.-M.Sc.,
Vyresnysis dėstytojas
V.G. Safonovas
Gomelis 2008 m
ĮVADAS
PAGRINDINIAI TRIGONOMETRINĖS LYGTIES SPRENDIMO METODAI
Faktorizavimas
Lygčių sprendimas paverčiant trigonometrinių funkcijų sandaugą į sumą
Lygčių sprendimas naudojant trigubo argumento formules
Padauginus iš kokios nors trigonometrinės funkcijos
NESTANDARTINĖS TRIGONOMETRINĖS LYGTYBĖS
TRIGONOMETRINĖS NELYGYBĖS
ŠAKNŲ PASIRINKIMAS
NEPRIKLAUSOMO SPRENDIMO UŽDUOTYS
IŠVADA
NAUDOTŲ ŠALTINIŲ SĄRAŠAS
Senovėje trigonometrija atsirado dėl astronomijos, žemės matavimo ir statybos poreikių, tai yra, ji buvo grynai geometrinio pobūdžio ir daugiausia atstovaujama.<<исчисление хорд>>. Laikui bėgant į jį ėmė įsiterpti kai kurie analitiniai momentai. XVIII amžiaus pirmoje pusėje įvyko staigus pokytis, po kurio trigonometrija įgavo naują kryptį ir perėjo prie matematinės analizės. Būtent tuo metu trigonometriniai santykiai buvo pradėti laikyti funkcijomis.
Trigonometrinės lygtys yra viena iš sunkiausių temų mokykliniame matematikos kurse. Trigonometrinės lygtys atsiranda sprendžiant planimetrijos, stereometrijos, astronomijos, fizikos ir kitų sričių uždavinius. Trigonometrinės lygtys ir nelygybės randamos tarp centralizuotų testavimo užduočių metai iš metų.
Svarbiausias skirtumas tarp trigonometrinių ir algebrinių lygčių yra tas, kad algebrinės lygtys turi baigtinį šaknų skaičių, o trigonometrinės lygtys --- begalinis, o tai labai apsunkina šaknų pasirinkimą. Kitas specifinis trigonometrinių lygčių bruožas yra neunikali atsakymo rašymo forma.
Šis darbas skirtas trigonometrinių lygčių ir nelygybių sprendimo būdams.
Darbą sudaro 6 skyriai.
Pirmajame skyriuje pateikiama pagrindinė teorinė informacija: trigonometrinių ir atvirkštinių trigonometrinių funkcijų apibrėžimas ir savybės; kai kurių argumentų trigonometrinių funkcijų verčių lentelė; trigonometrinių funkcijų išraiška kitų trigonometrinių funkcijų atžvilgiu, o tai labai svarbu transformuojant trigonometrines išraiškas, ypač turinčias atvirkštines išraiškas trigonometrinės funkcijos; Be pagrindinių trigonometrinių formulių, gerai žinomų iš mokyklos kurso, pateikiamos formulės, kurios supaprastina išraiškas, kuriose yra atvirkštinių trigonometrinių funkcijų.
Antrame skyriuje aprašomi pagrindiniai trigonometrinių lygčių sprendimo būdai. Nagrinėjamas elementariųjų trigonometrinių lygčių sprendimas, faktorizavimo metodas, trigonometrinių lygčių redukavimo į algebrines metodai. Dėl to, kad trigonometrinių lygčių sprendiniai gali būti rašomi keliais būdais, o šių sprendinių forma neleidžia iš karto nustatyti, ar šie sprendiniai yra vienodi ar skirtingi, o tai gali<<сбить с толку>> sprendžiant testus, atsižvelgiama į bendrą trigonometrinių lygčių sprendimo schemą ir detaliai nagrinėjama trigonometrinių lygčių bendrųjų sprendinių grupių transformacija.
Trečioje dalyje nagrinėjamos nestandartinės trigonometrinės lygtys, kurių sprendiniai paremti funkciniu požiūriu.
Ketvirtajame skyriuje aptariamos trigonometrinės nelygybės. Išsamiai aptariami elementarių uždavinių sprendimo būdai. trigonometrinės nelygybės, tiek vieneto apskritime, tiek grafiškai. Aprašytas neelementariųjų trigonometrinių nelygybių sprendimo elementariosiomis nelygybėmis procesas ir moksleiviams jau gerai žinomas intervalų metodas.
Penktoje dalyje pateikiamos sunkiausios užduotys: kai reikia ne tik išspręsti trigonometrinę lygtį, bet ir iš rastų šaknų atrinkti kokią nors sąlygą tenkinančias šaknis. Šiame skyriuje pateikiami tipinių šaknų pasirinkimo užduočių sprendimai. Pateikiama reikalinga teorinė informacija šaknims parinkti: sveikųjų skaičių aibės padalijimas į disjunktinius poaibius, lygčių sprendimas sveikaisiais skaičiais (diafantinas).
Šeštoje dalyje pateikiamos užduotys savarankiškas sprendimas, sukurtas testo forma. 20 testo užduočių yra sudėtingiausios užduotys, su kuriomis galima susidurti atliekant centralizuotą testavimą.
Elementariosios trigonometrinės lygtys
Elementariosios trigonometrinės lygtys yra formos lygtys, kur --- viena iš trigonometrinių funkcijų: , , , .
Elementariosios trigonometrinės lygtys turi begalinį šaknų skaičių. Pavyzdžiui, šios reikšmės atitinka lygtį: , , , ir tt. Bendroji formulė išilgai kurios randamos visos lygties šaknys, kur , yra:
Čia gali būti bet kokios sveikosios reikšmės, kiekviena iš jų atitinka konkrečią lygties šaknį; šioje formulėje (kaip ir kitose formulėse, kuriomis sprendžiamos elementarios trigonometrinės lygtys) vadinami parametras. Paprastai jie rašo , taip pabrėždami, kad parametras gali priimti bet kokias sveikųjų skaičių reikšmes.
Lygties , kur , sprendiniai randami pagal formulę
Lygtis išspręsta naudojant formulę
o lygtis yra pagal formulę
Ypač atkreipkime dėmesį į kai kuriuos specialius elementariųjų trigonometrinių lygčių atvejus, kai sprendinį galima parašyti nenaudojant bendrųjų formulių:
Sprendžiant trigonometrines lygtis svarbus vaidmuo vaidina trigonometrinių funkcijų periodą. Todėl pateikiame dvi naudingas teoremas:
Teorema Jei --- pagrindinis funkcijos periodas, tai skaičius yra pagrindinis funkcijos periodas.
Teigiama, kad funkcijų ir laikotarpiai yra palyginami, jei tokie yra sveikieji skaičiai Tai kas .
Teorema Jei periodinės funkcijos ir , turi proporcingas ir , tada jos turi bendrą laikotarpį, kuris yra funkcijų , , laikotarpis.
Teorema nurodo, kas yra funkcijos , , , periodas ir nebūtinai yra pagrindinis periodas. Pavyzdžiui, pagrindinis funkcijų laikotarpis ir --- , o pagrindinis jų gaminio laikotarpis --- .
Pristatome pagalbinį argumentą
Standartiniu formos išraiškų transformavimo būdu 
yra tokia technika: tegul --- kampas, pateiktos lygybės 
, 
. Bet kuriam toks kampas egzistuoja. Taigi. Jei , arba , , , kitais atvejais.
Trigonometrinių lygčių sprendimo schema
Pagrindinė schema, kuria vadovausimės spręsdami trigonometrines lygtis, yra tokia:
duotos lygties sprendimas redukuojamas į elementariųjų lygčių sprendimą. Sprendimai --- konversijos, faktorizavimas, nežinomųjų pakeitimas. Pagrindinis principas – neprarasti savo šaknų. Tai reiškia, kad pereidami prie kitos (-ių) lygties (-ių), mes nebijome papildomų (pašalinių) šaknų atsiradimo, o tik rūpinamės, kad kiekviena sekanti mūsų „grandinės“ lygtis (arba lygčių rinkinys šakojimo atveju ) yra ankstesnio pasekmė. Vienas iš galimi metodaišaknies pasirinkimas yra patikrinimas. Iš karto atkreipkime dėmesį, kad trigonometrinių lygčių atveju sunkumai, susiję su šaknų parinkimu ir tikrinimu, paprastai smarkiai padidėja, palyginti su algebrinėmis lygtimis. Juk turime patikrinti serijas, susidedančias iš begalinio skaičiaus terminų.
Sprendžiant trigonometrines lygtis ypatingai reikėtų paminėti nežinomųjų pakeitimą. Daugeliu atvejų po būtino pakeitimo gaunama algebrinė lygtis. Be to, lygtys nėra tokios retos, kad, nors ir yra trigonometrinės išvaizda, iš esmės jie nėra, nes po pirmojo žingsnio --- pakaitalai kintamieji --- virsta algebriniais, o grįžimas prie trigonometrijos įvyksta tik elementariųjų trigonometrinių lygčių sprendimo stadijoje.
Dar kartą priminsime: nežinomybės pakeitimas turi būti atliktas esant pirmai progai; po pakeitimo gauta lygtis turi būti išspręsta iki galo, įskaitant šaknų parinkimo etapą, ir tik tada grąžinama į pradinį nežinomybę.
Viena iš trigonometrinių lygčių ypatybių yra ta, kad atsakymas daugeliu atvejų gali būti parašytas Skirtingi keliai. Netgi norint išspręsti lygtį 
atsakymą galima parašyti taip:
1) dviejų serijų forma: 
, , ;
2) standartine forma, kuri yra minėtų eilučių derinys: , ;
3) nes 
, tada atsakymas gali būti parašytas formoje 
, . (Toliau, , , arba parametro buvimas atsakymo įraše automatiškai reiškia, kad šis parametras priima visas įmanomas sveikųjų skaičių reikšmes. Išimtys bus nurodytos.)
Akivaizdu, kad trys išvardyti atvejai neišsemia visų galimybių rašyti nagrinėjamos lygties atsakymą (jų yra be galo daug).
Pavyzdžiui, kai lygybė yra tiesa 
. Todėl pirmaisiais dviem atvejais, jei , galime pakeisti į .
Paprastai atsakymas rašomas remiantis 2 punktu. Gera prisiminti šią rekomendaciją: jei darbas nesibaigia lygties sprendimu, dar reikia atlikti tyrimus ir parinkti šaknis, tada 1 pastraipoje nurodyta patogiausia įrašymo forma. (Panašią rekomendaciją reikėtų pateikti ir lygčiai.)
Panagrinėkime pavyzdį, iliustruojantį tai, kas buvo pasakyta.
Pavyzdys Išspręskite lygtį.
Sprendimas. Akivaizdžiausias būdas yra toks. Ši lygtis suskirstyta į dvi dalis: ir . Išspręsdami kiekvieną iš jų ir sujungę gautus atsakymus, randame .
Kitas būdas. Nuo tada pakeičiant ir naudojant laipsnio mažinimo formules. Po nedidelių transformacijų gauname , iš kur 
.
Iš pirmo žvilgsnio antroji formulė neturi ypatingų pranašumų, palyginti su pirmąja. Tačiau jei paimtume, pavyzdžiui, tada išeina, kad, t.y. lygtis turi sprendimą, o pirmasis metodas veda mus prie atsakymo 
. „Pamatyk“ ir įrodyk lygybę 
ne taip lengva.
Atsakymas. .
Trigonometrinių lygčių bendrųjų sprendinių grupių konvertavimas ir jungimas
Mes svarstysime aritmetinė progresija, besitęsiantis be galo į abi puses. Šios progresijos narius galima suskirstyti į dvi narių grupes, esančias dešinėje ir kairėje nuo tam tikro nario, vadinamo centriniu arba nuliniu progresijos nariu.
Fiksuodami vieną iš begalinės progresijos narių nuliniu skaičiumi, turėsime atlikti dvigubą visų likusių narių numeraciją: teigiamą terminams, esantiems dešinėje, ir neigiamą terminams, esantiems kairėje nuo nulio.
Apskritai, jei progresijos skirtumas yra nulinis narys, bet kurio (-ojo) begalinės aritmetinės progresijos nario formulė yra tokia:
Bet kurio begalinės aritmetinės progresijos nario formulės transformacijos
1. Jei prie nulinio nario pridėsite arba atimsite progresijos skirtumą, tai progresija nepasikeis, o judės tik nulinis narys, t.y. Keisis narių numeracija.
2. Jei kintamosios reikšmės koeficientas padauginamas iš , tai tik lems dešinės ir kairiosios narių grupių pertvarkymą.
3. Jei begalinės progresijos nuoseklūs nariai
pavyzdžiui, , , ..., , paverskite centrinius progresijos narius su tuo pačiu skirtumu lygiu:
tada progresija ir progresijų serija išreiškia tuos pačius skaičius.
Pavyzdys Eilutę galima pakeisti šiomis trimis eilutėmis: , , .
4. Jei begalinės progresijos su tuo pačiu skirtumu kaip centriniai nariai turi skaičius, kurie sudaro aritmetinę progresiją su skirtumu , tai šias eilutes galima pakeisti viena progresija su skirtumu ir centriniu nariu, lygiu bet kuriam iš šių progresijų centrinių narių, t.y. Jeigu
tada šie progresai sujungiami į vieną:
Pavyzdys
... abu yra sujungti į vieną grupę, nes 
.
Norint paversti grupes, turinčias bendrų sprendimų, į grupes, kurios neturi bendrų sprendimų, šios grupės išskaidomos į grupes su bendru periodu, o tada bandoma sujungti gautas grupes, neįskaitant pasikartojančių.
Faktorizavimas
Faktorizacijos metodas yra toks: jei
tada kiekvienas lygties sprendinys
yra lygčių aibės sprendimas
Priešingas teiginys paprastai yra klaidingas: ne kiekvienas populiacijos sprendimas yra lygties sprendimas. Tai paaiškinama tuo, kad atskirų lygčių sprendiniai negali būti įtraukti į funkcijos apibrėžimo sritį.
Pavyzdys Išspręskite lygtį.
Sprendimas. Naudojant pagrindinį trigonometrinė tapatybė, pavaizduokime lygtį formoje
Atsakymas.
; 
.
Trigonometrinių funkcijų sumos pavertimas sandauga
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Taikydami formulę gauname ekvivalentinę lygtį
Atsakymas. .
Pavyzdys Išspręskite lygtį.
Sprendimas. IN tokiu atveju, prieš taikydami trigonometrinių funkcijų sumos formules, turėtumėte naudoti redukcijos formulę 
. Dėl to gauname lygiavertę lygtį
Atsakymas.
, 
.
Lygčių sprendimas paverčiant trigonometrinių funkcijų sandaugą į sumą
Sprendžiant daugybę lygčių, naudojamos formulės.
Pavyzdys Išspręskite lygtį
Sprendimas.
Atsakymas. , .
Pavyzdys Išspręskite lygtį.
Sprendimas. Taikydami formulę gauname lygiavertę lygtį:
Atsakymas. .
Lygčių sprendimas naudojant redukcijos formules
Sprendžiant platų trigonometrinių lygčių spektrą, pagrindinį vaidmenį atlieka formulės.
Pavyzdys Išspręskite lygtį.
Sprendimas. Taikydami formulę gauname lygiavertę lygtį.
Atsakymas. ; .
Lygčių sprendimas naudojant trigubo argumento formules
Pavyzdys Išspręskite lygtį.
Sprendimas. Taikydami formulę gauname lygtį
Atsakymas. ; .
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Taikydami laipsnio mažinimo formules gauname: 
. Kreipdamiesi gauname:
Atsakymas. ; .
To paties pavadinimo trigonometrinių funkcijų lygybė
Pavyzdys Išspręskite lygtį.
Sprendimas.
Atsakymas. , .
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Transformuokime lygtį.
Atsakymas. .
Pavyzdys Yra žinoma, kad ir patenkinti lygtį
Raskite sumą.
Sprendimas. Iš lygties išplaukia, kad
Atsakymas. .
Panagrinėkime formos sumas
Šias sumas galima paversti produktu, padauginus ir padalijus iš, tada gauname
Ši technika gali būti naudojama sprendžiant kai kurias trigonometrines lygtis, tačiau reikia turėti omenyje, kad dėl to gali atsirasti pašalinių šaknų. Apibendrinkime šias formules:
Pavyzdys Išspręskite lygtį.
Sprendimas. Matyti, kad aibė yra pradinės lygties sprendimas. Todėl padauginus kairę ir dešinę lygties puses iš papildomų šaknų neatsiras.
Mes turime 
.
Atsakymas. ; .
Pavyzdys Išspręskite lygtį.
Sprendimas. Padauginkime kairę ir dešinę lygties puses iš ir pritaikykime trigonometrinių funkcijų sandaugos pavertimo į sumą formules, gausime
Ši lygtis yra lygiavertė dviejų lygčių ir , iš kur ir , deriniui.
Kadangi lygties šaknys nėra lygties šaknys, turėtume neįtraukti . Tai reiškia, kad rinkinyje būtina išskirti .
Atsakymas. Ir,.
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Pakeiskime išraišką:
Lygtis bus parašyta taip:
Atsakymas. .
Trigonometrinių lygčių redukavimas į algebrines
Sumažinamas iki kvadrato
Jei lygtis yra tokios formos
tada pakeitimas veda į kvadratą, nes 
() Ir.
Jei vietoj termino yra , tada būtinas pakeitimas bus .
Lygtis
nusileidžia iki kvadratinė lygtis
pristatymas kaip 
. Nesunku patikrinti, ar kurioms , nėra lygties šaknys, o pakeitus , lygtis sumažinama iki kvadratinės.
Pavyzdys Išspręskite lygtį.
Sprendimas. Perkelkime jį į kairę pusę, pakeiskime , ir išreikškime per ir .
Supaprastinus gauname: . Padalinkite terminą iš termino ir pakeiskite:
Grįžę į , randame 
.
Lygtys homogeniškos atžvilgiu ,
Apsvarstykite formos lygtį
Kur , , , ..., , --- galioja numeriai. Kiekviename kairėje lygties pusėje esančiame dėmenyje monomijų laipsniai yra lygūs, tai yra, sinuso ir kosinuso laipsnių suma yra vienoda ir lygi. Ši lygtis vadinama vienalytis palyginti su ir , ir numeris yra vadinamas homogeniškumo rodiklis .
Akivaizdu, kad jei , tada lygtis bus tokia:
kurių sprendiniai yra reikšmės, kuriose , ty skaičiai , . Antroji lygtis, parašyta skliausteliuose, taip pat yra vienalytė, tačiau laipsniai yra 1 mažesni.
Jei , tai šie skaičiai nėra lygties šaknys.
Kai gauname: , o kairėje lygties pusėje (1) įgyjama reikšmė .
Taigi, ir , Todėl galime padalyti abi lygties puses iš . Dėl to gauname lygtį:
kurią pakeičiant galima lengvai redukuoti į algebrinę:
Homogeninės lygtys su vienarūšiškumo indeksu 1. Kai turime lygtį .
Jei , tai ši lygtis yra lygi lygčiai , , iš kur , .
Pavyzdys Išspręskite lygtį.
Sprendimas.Ši lygtis yra pirmojo laipsnio vienalytė. Abi dalis padaliname iš: , , , .
Atsakymas. .
Pavyzdys Kai gauname vienalytę formos lygtį
Sprendimas.
Jei , tada padalykite abi lygties puses iš , gausime lygtį 
, kurį galima lengvai sumažinti į kvadratą pakeičiant: 
. Jeigu 
, tada lygtis turi realias šaknis , . Pradinė lygtis turės dvi sprendinių grupes: , , .
Jeigu 
, tada lygtis neturi sprendinių.
Pavyzdys Išspręskite lygtį.
Sprendimas.Ši lygtis yra antrojo laipsnio vienalytė. Abi lygties puses padaliname iš , gauname: . Leiskite , tada , , . , , ; ...
Atsakymas.
.
Lygtis sumažinama iki formos lygties
Norėdami tai padaryti, pakanka naudoti tapatybę 
Visų pirma lygtis sumažinama iki vienalytės, jei ją pakeisime 
, tada gauname lygiavertę lygtį:
Pavyzdys Išspręskite lygtį.
Sprendimas. Paverskime lygtį į vienalytę:
Abi lygties puses padalinkime iš 
, gauname lygtį:
Leiskite , tada prieisime prie kvadratinės lygties: , , 
, 
, .
Atsakymas.
.
Pavyzdys Išspręskite lygtį.
Sprendimas. Padėkime kvadratu abi lygties puses, atsižvelgiant į tai, kad jos turi teigiamas vertes: , ,
Tegul būna, tada gausime 
, , .
Atsakymas. .
Lygtys išspręstos naudojant tapatybes 
Naudinga žinoti šias formules:
Pavyzdys Išspręskite lygtį.
Sprendimas. Naudodami, gauname
Atsakymas.
Siūlome ne pačias formules, o jų išvedimo būdą:
vadinasi,
Taip pat, .
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Pakeiskime išraišką:
Lygtis bus parašyta taip:
Priimdami mes gauname. , . Vadinasi
Atsakymas. .
Universalus trigonometrinis pakeitimas
Trigonometrinė formos lygtis
Kur --- racionalus funkcija formulių pagalba - , taip pat formulių pagalba - gali būti sumažinta iki racionalioji lygtis atsižvelgiant į argumentus , , , po kurių lygtis gali būti sumažinta iki algebrinės racionalios lygties, atsižvelgiant į universalaus trigonometrinio pakeitimo formules
Pažymėtina, kad dėl formulių naudojimo gali susiaurėti pradinės lygties OD, kadangi ji nėra apibrėžta taškuose, todėl tokiais atvejais reikia patikrinti, ar kampai yra pradinės lygties šaknys. .
Pavyzdys Išspręskite lygtį.
Sprendimas. Pagal užduoties sąlygas. Pritaikę formules ir atlikę keitimą, gauname
iš kur ir todėl .
Formos lygtys
Formos lygtys , kur --- daugianario, išsprendžiami naudojant nežinomųjų pakaitalus
Pavyzdys Išspręskite lygtį.
Sprendimas. Pakeitę ir atsižvelgdami į tai, gauname
kur,. --- pašalinisšaknis, nes . Lygties šaknys 
yra .
Funkcijos apribojimų naudojimas
Centralizuoto testavimo praktikoje ne taip retai tenka susidurti su lygtimis, kurių sprendimas grindžiamas ribotomis funkcijomis ir . Pavyzdžiui:
Pavyzdys Išspręskite lygtį.
Sprendimas. Kadangi , Tada kairioji pusė neviršija ir yra lygi , Jei
Norėdami rasti vertes, kurios tenkina abi lygtis, elgiamės taip. Išspręskime vieną iš jų, tada iš rastų verčių pasirinksime tas, kurios tenkina kitą.
Pradėkime nuo antrojo: , . Tada, 
.
Aišku, kad tik lyginiams skaičiams bus .
Atsakymas. .
Kita idėja įgyvendinama sprendžiant šią lygtį:
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Naudokimės turtu eksponentinė funkcija: , 
.
Sudėjus šias nelygybes po termino, gauname:
Todėl kairioji šios lygties pusė yra lygi tada ir tik tada, kai tenkinamos dvi lygybės:
y., jis gali perimti reikšmes , , arba gali perimti reikšmes, .
Atsakymas. , .
Pavyzdys
Išspręskite lygtį 
.
Sprendimas., . Vadinasi, 
.
Atsakymas. .
Pavyzdys Išspręskite lygtį
Sprendimas. Pažymėkime , tada iš atvirkštinės trigonometrinės funkcijos apibrėžimo turime 
Ir 
.
Kadangi, tada iš lygties išplaukia nelygybė, t.y. . Nuo ir , tada ir . Tačiau dėl to.
Jei ir tada. Kadangi anksčiau buvo nustatyta, kad .
Atsakymas. , .
Pavyzdys Išspręskite lygtį
Sprendimas. Regionas priimtinos vertės lygtys yra.
Pirmiausia parodome, kad funkcija
Bet kuriam tai gali būti tik teigiamos vertės.
Įsivaizduokime funkciją taip: .
Nuo tada jis vyksta, t.y. 
.
Todėl norint įrodyti nelygybę, būtina tai parodyti 
. Šiuo tikslu supjaustykime abi šios nelygybės puses
Gauta skaitinė nelygybė rodo, kad . Jei taip pat atsižvelgsime į tai, tada kairioji lygties pusė yra neneigiama.
Dabar pažvelkime į dešinę lygties pusę.
Nes 
, Tai
Tačiau yra žinoma, kad 
. Iš to seka, kad t.y. dešinioji lygties pusė neviršija . Anksčiau buvo įrodyta, kad kairioji lygties pusė yra ne neigiama, todėl lygybė gali įvykti tik tuo atveju, jei abi pusės yra lygios, ir tai įmanoma tik tuo atveju, jei .
Atsakymas. .
Pavyzdys Išspręskite lygtį
Sprendimas. Pažymime ir 
. Taikydami Koši-Buniakovskio nelygybę, gauname . Tai seka 
. Kita vertus, yra 
. Todėl lygtis neturi šaknų.
Atsakymas. .
Pavyzdys Išspręskite lygtį:
Sprendimas. Perrašykime lygtį taip:
Atsakymas. .
Funkciniai trigonometrinių ir kombinuotųjų lygčių sprendimo metodai
Ne kiekviena lygtis dėl transformacijų gali būti redukuojama į vieną ar kitą lygtį standartinis vaizdas, kuriam yra konkretus sprendimo būdas. Tokiais atvejais naudinga naudoti tokias funkcijų savybes kaip monotoniškumas, ribojimas, paritetas, periodiškumas ir kt. Taigi, jei viena iš funkcijų intervale mažėja, o antroji didėja, tai jei lygtis turi šaknis šiame intervale, ši šaknis yra unikali, ir tada, pavyzdžiui, ją galima rasti pasirinkus. Jei funkcija ribojama aukščiau ir , o funkcija apribota žemiau ir , tada lygtis yra lygiavertė lygčių sistemai
Pavyzdys Išspręskite lygtį
Sprendimas. Pradinę lygtį paverskime forma
ir išspręskite jį kaip kvadratinį santykį su . Tada gauname,
Išspręskime pirmąją populiacijos lygtį. Atsižvelgdami į ribotą funkcijos pobūdį, darome išvadą, kad lygtis gali turėti tik segmento šaknį. Šiuo intervalu funkcija didėja, o funkcija 
mažėja. Todėl, jei ši lygtis turi šaknį, ji yra unikali. Randame pagal atranką.
Atsakymas. .
Pavyzdys Išspręskite lygtį
Sprendimas. Leiskite ir 
, tada pradinę lygtį galima parašyti kaip funkcinę lygtį. Kadangi funkcija yra nelyginė, tada . Šiuo atveju gauname lygtį.
Kadangi , ir yra monotoniškas , lygtis yra lygiavertė lygčiai, t.y. 
, kuris turi vieną šaknį.
Atsakymas. .
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Remiantis išvestine teorema sudėtinga funkcija aišku, kad funkcija 
mažėja (funkcija mažėja, didėja, mažėja). Iš to aišku, kad funkcija 
apibrėžta , mažėja. Todėl ši lygtis turi daugiausia vieną šaknį. Nes 
, Tai
Atsakymas. .
Pavyzdys Išspręskite lygtį.
Sprendimas. Panagrinėkime lygtį trimis intervalais.
a) Tegul . Tada šioje aibėje pradinė lygtis yra lygi lygčiai . Kuris neturi sprendimų dėl intervalo, nes 
, , A. Intervale pradinė lygtis taip pat neturi šaknų, nes 
, A.
b) Tegul . Tada šioje aibėje pradinė lygtis yra lygi lygčiai
kurių šaknys intervale yra skaičiai , , , .
c) Tegul . Tada šioje aibėje pradinė lygtis yra lygi lygčiai
Kuris neturi sprendimų intervale, nes , ir . Intervale lygtis taip pat neturi sprendinių, nes , , A.
Atsakymas. , , , .
Simetrijos metodas
Simetrijos metodą patogu naudoti, kai formuluojant užduotį reikia unikalaus lygties, nelygybės, sistemos ir pan. sprendimo. arba tiksli sprendinių skaičiaus nuoroda. Tokiu atveju turėtų būti aptikta bet kokia pateiktų išraiškų simetrija.
Taip pat būtina atsižvelgti į įvairių rūšių įvairovę galimi tipai simetrija.
Ne mažiau svarbu yra griežtas loginių etapų laikymasis samprotaujant su simetrija.
Paprastai simetrija leidžia tik nustatyti būtinas sąlygas, o tada reikia patikrinti jų pakankamumą.
Pavyzdys Raskite visas parametro reikšmes, kurių lygtis turi unikalų sprendimą.
Sprendimas. Atkreipkite dėmesį, kad ir --- net funkcijos, taigi kairioji lygties pusė yra lygi funkcija.
Taigi, jei --- sprendimas lygtys, tai yra ir lygties sprendimas. Jeigu --- vienintelis dalykas lygties sprendimas, tada būtina , .
Mes pasirinksime galima vertes, reikalaujant, kad tai būtų lygties šaknis.
Iš karto atkreipkime dėmesį, kad kitos vertybės negali patenkinti problemos sąlygų.
Tačiau dar nėra žinoma, ar visi atrinktieji iš tikrųjų atitinka užduoties sąlygas.
Tinkamumas.
1), lygtis įgis tokią formą 
.
2), lygtis bus tokia:
Akivaizdu, kad kiekvienam ir 
. Todėl paskutinė lygtis yra lygiavertė sistemai:
Taigi, mes įrodėme, kad lygtis turi unikalų sprendimą.
Atsakymas. .
Sprendimas su funkcijų tyrimu
Pavyzdys Įrodykite, kad visi lygties sprendiniai
Sveiki skaičiai.
Sprendimas. Pagrindinis pradinės lygties laikotarpis yra . Todėl pirmiausia išnagrinėjame šią lygtį intervale.
Transformuokime lygtį į formą:
Naudodami mikroskaičiuotuvą gauname:
Jei , tai iš ankstesnių lygybių gauname:
Išsprendę gautą lygtį, gauname: .
Atlikti skaičiavimai leidžia daryti prielaidą, kad segmentui priklausančios lygties šaknys yra , ir .
Tiesioginis bandymas patvirtina šią hipotezę. Taigi buvo įrodyta, kad lygties šaknys yra tik sveikieji skaičiai , .
Pavyzdys
Išspręskite lygtį 
.
Sprendimas. Raskime pagrindinį lygties periodą. Funkcija turi pagrindinį laikotarpį, lygų . Pagrindinis funkcijos laikotarpis yra . Mažiausias bendras kartotinis ir yra lygus . Todėl pagrindinis lygties laikotarpis yra . Leisti .
Akivaizdu, kad tai lygties sprendimas. Ant intervalo. Funkcija yra neigiama. Todėl kitų lygties šaknų reikia ieškoti tik intervaluose x ir .
Naudodami mikroskaičiuotuvą pirmiausia randame apytiksles lygties šaknų reikšmes. Norėdami tai padaryti, sudarome funkcijų reikšmių lentelę 
apie intervalus ir ; y. ant intervalų ir .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Iš lentelės nesunkiai išskiriamos šios hipotezės: segmentui priklausančios lygties šaknys yra skaičiai: ; ; . Tiesioginis bandymas patvirtina šią hipotezę.
Atsakymas.
; 
; .
Trigonometrinių nelygybių sprendimas naudojant vienetinį apskritimą
Sprendžiant formos trigonometrines nelygybes, kur yra viena iš trigonometrinių funkcijų, patogu naudoti trigonometrinį apskritimą, kad būtų kuo aiškiausiai pavaizduoti nelygybės sprendiniai ir užrašytas atsakymas. Pagrindinis trigonometrinių nelygybių sprendimo būdas yra jas redukuoti iki paprasčiausių tipo nelygybių. Pažvelkime į pavyzdį, kaip išspręsti tokias nelygybes.
Pavyzdys Išspręskite nelygybę.
Sprendimas. Nubrėžkime trigonometrinį apskritimą ir pažymėkime jame taškus, kurių ordinatės viršija .
Šios nelygybės sprendimas bus . Taip pat aišku, kad jei tam tikras skaičius nuo bet kurio nurodyto intervalo skaičiaus skiriasi , tai jis taip pat bus ne mažesnis nei . Todėl tereikia pridėti rasto sprendimo segmento galus. Galiausiai pamatome, kad pradinės nelygybės sprendimai bus visi 
.
Atsakymas.
.
Norint išspręsti nelygybes su liestine ir kotangentu, naudinga liestinių ir kotangentų linijos sąvoka. Tai yra tiesės ir atitinkamai (1 ir 2 paveiksluose) trigonometrinio apskritimo liestinės.
Nesunku suprasti, kad jei sukonstruosime spindulį, kurio pradžia yra koordinačių pradžioje, sudarydami kampą su teigiama abscisių ašies kryptimi, tada atkarpos ilgis nuo taško iki šio spindulio susikirtimo taško liestinės linija yra tiksliai lygi kampo, kurį šis spindulys sudaro su abscisių ašimi, liestei. Panašus stebėjimas vyksta ir kotangentui.
Pavyzdys Išspręskite nelygybę.
Sprendimas. Pažymime , tada nelygybė įgis paprasčiausią formą: . Panagrinėkime ilgio intervalą, lygų mažiausiam teigiamam liestinės periodui (LPP). Šiame segmente, naudodamiesi liestinių linija, nustatome, kad . Dabar prisiminkime, ką reikia pridėti, nes AE veikia. Taigi, 
. Grįžę prie kintamojo, gauname tai.
Atsakymas.
.
Nelygybes su atvirkštinėmis trigonometrinėmis funkcijomis patogu spręsti naudojant atvirkštinių trigonometrinių funkcijų grafikus. Parodykime, kaip tai daroma pavyzdžiu.
Trigonometrinių nelygybių sprendimas grafiškai
Atkreipkite dėmesį, kad jei yra periodinė funkcija, tai norint išspręsti nelygybę, reikia rasti jos sprendimą atkarpoje, kurios ilgis lygus funkcijos periodui. Visus pradinės nelygybės sprendinius sudarys rastos reikšmės, taip pat visi tie, kurie skiriasi nuo rastų bet kokiu sveikuoju funkcijos periodų skaičiumi.
Panagrinėkime nelygybės sprendimą ().
Nuo tada nelygybė neturi sprendimų. Jei , tai nelygybės sprendinių rinkinys --- krūva visi tikrieji skaičiai.
Leisti . Sinuso funkcija turi mažiausią teigiamą periodą, todėl nelygybę pirmiausia galima išspręsti ilgio atkarpoje, pavyzdžiui, atkarpoje. Mes sudarome funkcijų grafikus ir (). yra pateikiamos formos nelygybės: ir iš kur,
Šiame darbe buvo nagrinėjami trigonometrinių lygčių ir nelygybių sprendimo būdai tiek paprastų, tiek olimpiados lygiu. Svarstyti pagrindiniai trigonometrinių lygčių ir nelygybių sprendimo būdai, be to, kaip specifiniai --- charakteristika tik trigonometrinėms lygtims ir nelygybėms bei bendriesiems funkciniams lygčių ir nelygybių sprendimo metodams, kurie taikomi trigonometrinėms lygtims.
Baigiamajame darbe pateikiama pagrindinė teorinė informacija: trigonometrinių ir atvirkštinių trigonometrinių funkcijų apibrėžimas ir savybės; trigonometrinių funkcijų išreiškimas kitomis trigonometrinėmis funkcijomis, o tai labai svarbu transformuojant trigonometrines išraiškas, ypač turinčias atvirkštines trigonometrines funkcijas; Be pagrindinių trigonometrinių formulių, gerai žinomų iš mokyklos kurso, pateikiamos formulės, kurios supaprastina išraiškas, kuriose yra atvirkštinių trigonometrinių funkcijų. Nagrinėjamas elementariųjų trigonometrinių lygčių sprendimas, faktorizavimo metodas, trigonometrinių lygčių redukavimo į algebrines metodai. Atsižvelgiant į tai, kad trigonometrinių lygčių sprendiniai gali būti rašomi keliais būdais, o šių sprendinių forma neleidžia iš karto nustatyti, ar šie sprendiniai yra vienodi ar skirtingi, nagrinėjama bendra trigonometrinių lygčių sprendimo schema ir transformacija. Išsamiai nagrinėjama trigonometrinių lygčių bendrųjų sprendinių grupių. Išsamiai aptariami elementariųjų trigonometrinių nelygybių sprendimo vienetiniame apskritime ir grafiniu metodu metodai. Aprašytas neelementariųjų trigonometrinių nelygybių sprendimo elementariosiomis nelygybėmis procesas ir moksleiviams jau gerai žinomas intervalų metodas. Pateikiami tipinių šaknų atrankos užduočių sprendimai. Pateikiama reikalinga teorinė informacija šaknims parinkti: sveikųjų skaičių aibės padalijimas į disjunktinius poaibius, lygčių sprendimas sveikaisiais skaičiais (diafantinas).
Šio baigiamojo darbo rezultatai gali būti naudojami kaip mokomoji medžiaga rengiant kursinius darbus ir tezės, rengiant pasirenkamuosius dalykus moksleiviams, darbas gali būti panaudotas ir ruošiant studentus stojamiesiems egzaminams bei centralizuotam testavimui.
Vygodsky Ya.Ya., Elementariosios matematikos vadovas. / Vygodsky Ya.Ya. --- M.: Nauka, 1970 m.
Igudisman O., Matematika egzamine žodžiu / Igudisman O. --- M.: Iris Press, Rolf, 2001 m.
Azarov A.I., lygtys / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Mn.: Trivium, 1994 m.
Litvinenka V.N., Pradinės matematikos seminaras / Litvinenka V.N. --- M.: Švietimas, 1991 m.
Sharygin I.F., Pasirenkamas matematikos kursas: problemų sprendimas / Sharygin I.F., Golubev V.I. --- M.: Išsilavinimas, 1991 m.
Barduškinas V., Trigonometrinės lygtys. Šaknies pasirinkimas/B. Barduškinas, A. Prokofjevas.// Matematika, Nr. 12, 2005 p. 23--27.
Vasilevsky A.B., Užklasinio darbo užduotys matematikos srityje/Vasilevsky A.B. --- Mn.: Liaudies Asveta. 1988. --- 176 p.
Sapunov P. I., Trigonometrinių lygčių bendrųjų sprendinių grupių transformacija ir sujungimas / Sapunov P. I. // Matematinis ugdymas, 1935 m. 3 leidimas.
Borodinas P., Trigonometrija. Medžiagos stojamieji egzaminai Maskvos valstybiniame universitete [tekstas]/P. Borodinas, V. Galkinas, V. Panferovas, I. Sergejevas, V. Tarasovas // Matematika Nr. 1, 2005 p. 36--48.
Samusenko A.V., Matematika: Daznos klaidos pareiškėjai: žinynas/Samusenko A.V., Kazachenok V.V. --- Mn.: Aukštoji mokykla, 1991 m.
Azarov A.I., Funkciniai ir grafiniai tyrimo uždavinių sprendimo metodai / Azarov A.I., Barvenov S.A., --- Mn.: Aversev, 2004.
Paprastų trigonometrinių nelygybių sprendimo algoritmas ir trigonometrinių nelygybių sprendimo būdų atpažinimas.
Aukštųjų mokyklų dėstytojai kvalifikacinė kategorija:
Shirko F.M. p.Pažanga, MOBU-vidurinė mokykla Nr
Sankina L.S. Armavir, privati vidurinė mokykla Naujas būdas»
Nėra universalių gamtos mokslų ir matematikos disciplinų mokymo metodų. Kiekvienas mokytojas randa savo tik jam priimtinus mokymo būdus.
Mūsų ilgametė dėstymo patirtis rodo, kad studentai lengviau išmoksta medžiagą, kuri reikalauja susikaupimo ir didelio informacijos kiekio atmintyje išsaugojimo, jei pradiniame mokymosi etape mokomi naudoti algoritmus savo veikloje. sudėtinga tema. Mūsų nuomone, tokia tema yra trigonometrinių nelygybių sprendimo tema.
Taigi, prieš pradėdami su studentais nustatyti trigonometrinių nelygybių sprendimo būdus ir metodus, praktikuojame ir sutvirtiname paprasčiausių trigonometrinių nelygybių sprendimo algoritmą.
Paprastų trigonometrinių nelygybių sprendimo algoritmas
Pažymėkite taškus atitinkamoje ašyje ( Dėl nuodėmė x– OA ašis, skirtacos x– OX ašis)
Atkuriame statmeną ašiai, kuri kirs apskritimą dviejuose taškuose.
Pirmasis apskritimo taškas yra taškas, kuris pagal apibrėžimą priklauso lanko funkcijų diapazono intervalui.
Pradėdami nuo pažymėto taško, užtemdykite apskritimo lanką, atitinkantį užtemdytą ašies dalį.
Atkreipkite dėmesį Ypatingas dėmesysį aplinkkelio kryptį. Jei važiuojama pagal laikrodžio rodyklę (t. y. yra perėjimas per 0), tada antrasis apskritimo taškas bus neigiamas, jei prieš laikrodžio rodyklę – teigiamas.
Atsakymą rašome intervalo forma, atsižvelgdami į funkcijos periodiškumą.
Pažvelkime į algoritmo veikimą naudodamiesi pavyzdžiais.
1) nuodėmė ≥ 1/2;
Sprendimas:
Vaizduojame vienetinį apskritimą.;
OU ašyje pažymime tašką ½.
Atkuriame statmeną ašiai,
kuri kerta apskritimą dviejuose taškuose.
Pagal arcsinuso apibrėžimą pirmiausia atkreipiame dėmesį
taškas π/6.
Nuspalvinkite tą ašies dalį, kuri atitinka
duota nelygybė, virš taško ½.
Nuspalvinkite apskritimo lanką, atitinkantį užtamsintą ašies dalį.
Važiuojama prieš laikrodžio rodyklę, gauname tašką 5π/6.
Atsakymą rašome intervalo forma, atsižvelgdami į funkcijos periodiškumą;
Atsakymas:x;[π/6 + 2π n, 5π/6 + 2π n], n Z.
Paprasčiausia nelygybė išsprendžiama naudojant tą patį algoritmą, jei atsakymo įraše nėra lentelės reikšmės.
Mokiniai, spręsdami nelygybes prie lentos pirmose pamokose, garsiai kartoja kiekvieną algoritmo žingsnį.
2) 5 cos x – 1 ≥ 0;
R 
sprendimas:adresu
5 cos x – 1 ≥ 0;
cos x ≥ 1/5;
Nubrėžkite vieneto apskritimą.
OX ašyje pažymime tašką, kurio koordinatė yra 1/5.
Atstatome statmeną ašiai, kuri
kerta apskritimą dviejuose taškuose.
Pirmasis apskritimo taškas yra taškas, priklausantis lanko kosinuso diapazono intervalui pagal apibrėžimą (0;π).
Užtamsiname šią nelygybę atitinkančią ašies dalį.
Pradedant nuo pasirašyto taško arccos 1/5, užtemdykite apskritimo lanką, atitinkantį užtamsintą ašies dalį.
Važiuojama pagal laikrodžio rodyklę (t. y. yra perėjimas per 0), o tai reiškia, kad antrasis apskritimo taškas bus neigiamas - arccos 1/5.
Atsakymą rašome intervalo forma, atsižvelgdami į funkcijos periodiškumą, nuo mažesnės reikšmės iki didesnės.
Atsakymas: x [-arccos 1/5 + 2π n, arccos 1/5 + 2π n], n Z.
Tobulinti gebėjimą spręsti trigonometrines nelygybes palengvina šie klausimai: „Kaip išspręsime nelygybių grupę?“; „Kuo viena nelygybė skiriasi nuo kitos?“; „Kuo viena nelygybė panaši į kitą?“; Kaip pasikeistų atsakymas, jei būtų pateikta griežta nelygybė?“; Kaip pasikeistų atsakymas, jei vietoj ženklo „“ būtų ženklas „
Užduotis analizuoti nelygybių sąrašą jų sprendimo metodų požiūriu leidžia praktikuoti jų atpažinimą.
Mokiniams pateikiamos nelygybės, kurias reikia išspręsti klasėje.
Klausimas: Pabrėžkite nelygybes, kurioms reikia naudoti ekvivalentines transformacijas, kai trigonometrinė nelygybė sumažinama iki paprasčiausios formos?
Atsakymas 1, 3, 5.
Klausimas: Kokios yra nelygybės, kai sudėtingą argumentą reikia laikyti paprastu?
Atsakymas: 1, 2, 3, 5, 6.
Klausimas:Įvardykite nelygybes, kur jas galima pritaikyti trigonometrines formules?
Atsakymas: 2, 3, 6.
Klausimas:Įvardykite nelygybes, kuriose galima pritaikyti naujo kintamojo įvedimo metodą?
Atsakymas: 6.
Užduotis analizuoti nelygybių sąrašą jų sprendimo metodų požiūriu leidžia praktikuoti jų atpažinimą. Ugdant įgūdžius svarbu nustatyti jo įgyvendinimo etapus ir juos suformuluoti bendras vaizdas, kuris pateiktas paprasčiausių trigonometrinių nelygybių sprendimo algoritme.
Algebros projektą „Trigonometrinių nelygybių sprendimas“ užbaigė 10 „B“ klasės mokinė Kazachkova Julija Vadovas: matematikos mokytoja Kochakova N.N.
Tikslas Sutvirtinti medžiagą tema „Trigonometrinių nelygybių sprendimas“ ir sukurti priminimą mokiniams pasiruošti būsimam egzaminui.
Tikslai: Apibendrinti medžiagą šia tema. Susisteminkite gautą informaciją. Apsvarstykite šią temą vieningame valstybiniame egzamine.
Aktualumas Mano pasirinktos temos aktualumas slypi tuo, kad užduotys tema „Trigonometrinių nelygybių sprendimas“ yra įtrauktos į vieningo valstybinio egzamino užduotis.
Trigonometrinės nelygybės Nelygybė yra ryšys, jungiantis du skaičius arba išraiškas per vieną iš ženklų: (didesnis už); ≥ (didesnis arba lygus). Trigonometrinė nelygybė yra nelygybė, apimanti trigonometrines funkcijas.
Trigonometrinės nelygybės Nelygybių, turinčių trigonometrines funkcijas, sprendimas, kaip taisyklė, redukuojamas iki paprasčiausių formos nelygybių: sin x>a, sin x a, cos x a, tg x a,ctg x
Trigonometrinių nelygybių sprendimo algoritmas Ant ašies, atitinkančios duotą trigonometrinę funkciją, pažymėkite tai skaitinė reikšmėšią funkciją. Per pažymėtą tašką nubrėžkite liniją, kertančią vienetinį apskritimą. Atsižvelgdami į griežtą arba negriežtą nelygybės ženklą, pasirinkite tiesės ir apskritimo susikirtimo taškus. Pasirinkite apskritimo, kuriame yra nelygybės sprendiniai, lanką. Nustatykite kampo reikšmes apskritimo lanko pradžios ir pabaigos taškuose. Atsižvelgdami į duotosios trigonometrinės funkcijos periodiškumą, užrašykite nelygybės sprendinį.
Trigonometrinių nelygybių sinx >a sprendimo formulės; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosxa; x (arctg a + πn ; + πn). tgx a; x (πn ; arctan + πn). ctgx
Grafinis sprendimas pagrindinės trigonometrinės nelygybės sinx >a
Pagrindinių trigonometrinių nelygybių sinx grafinis sprendimas Pagrindinių trigonometrinių nelygybių cosx >a grafinis sprendimas Grafinis pagrindinių trigonometrinių nelygybių cosx sprendimas Pagrindinių trigonometrinių nelygybių tgx >a grafinis sprendimas Grafinis pagrindinių trigonometrinių nelygybių tgx sprendimas Grafinis pagrindinių trigonometrinių nelygybių sprendimas ctgx >a
Sprendžiant nelygybes, turinčias trigonometrines funkcijas, jos redukuojamos į paprasčiausias formos cos(t)>a, sint(t)=a ir panašias nelygybes. Ir jau išspręstos paprasčiausios nelygybės. Pažiūrėkime įvairių pavyzdžių paprastų trigonometrinių nelygybių sprendimo būdai.
1 pavyzdys. Išspręskite nelygybę sin(t) > = -1/2.
Nubrėžkite vieneto apskritimą. Kadangi sin(t) pagal apibrėžimą yra y koordinatė, Oy ašyje pažymime tašką y = -1/2. Per ją nubrėžiame tiesią liniją, lygiagrečią Ox ašiai. Tiesės sankirtoje su vienetinio apskritimo grafiku pažymėkite taškus Pt1 ir Pt2. Sujungiame koordinačių pradžią su taškais Pt1 ir Pt2 dviem atkarpomis.
Šios nelygybės sprendimas bus visi vienetinio apskritimo taškai, esantys virš šių taškų. Kitaip tariant, sprendimas bus lankas l. Dabar reikia nurodyti sąlygas, kurioms esant savavališkas taškas priklausys lankui l.
Pt1 yra dešiniajame puslankiu, jo ordinatė yra -1/2, tada t1=arcsin(-1/2) = - pi/6. Norėdami apibūdinti tašką Pt1, galite parašyti šią formulę:
t2 = pi – arcsin(-1/2) = 7*pi/6. Dėl to gauname tokią t nelygybę:
Išsaugome nelygybę. O kadangi sinuso funkcija yra periodinė, tai reiškia, kad sprendimai bus kartojami kas 2*pi. Šią sąlygą pridedame prie gautos t nelygybės ir užrašome atsakymą.
Atsakymas: -pi/6+2*pi*n< = t < = 7*pi/6 + 2*pi*n, при любом целом n.
2 pavyzdys. Išspręskite cos(t) nelygybę<1/2.
Nubraižykime vienetinį apskritimą. Kadangi pagal apibrėžimą cos(t) yra x koordinatė, Ox ašies grafike pažymime tašką x = 1/2.
Per šį tašką nubrėžiame tiesią liniją, lygiagrečią Oy ašiai. Tiesės sankirtoje su vienetinio apskritimo grafiku pažymėkite taškus Pt1 ir Pt2. Sujungiame koordinačių pradžią su taškais Pt1 ir Pt2 dviem atkarpomis.
Sprendimai bus visi vienetinio apskritimo taškai, priklausantys lankui l. Raskime taškus t1 ir t2.
t1 = arccos(1/2) = pi/3.
t2 = 2*pi – arccos(1/2) = 2*pi-pi/3 = 5*pi/6.
Gavome t nelygybę: pi/3 Kadangi kosinusas yra periodinė funkcija, sprendimai bus kartojami kas 2*pi. Šią sąlygą pridedame prie gautos t nelygybės ir užrašome atsakymą. Atsakymas: pi/3+2*pi*n 3 pavyzdys. Išspręskite nelygybę tg(t)< = 1. Tangento periodas lygus pi. Raskime sprendinius, priklausančius intervalo (-pi/2;pi/2) dešiniajam puslankiui. Toliau, naudodamiesi liestinės periodiškumu, užrašome visus šios nelygybės sprendinius. Nubrėžkime vienetinį apskritimą ir pažymėkime jame liestinių liniją. Jei t yra nelygybės sprendimas, tai taško T = tg(t) ordinatė turi būti mažesnė arba lygi 1. Tokių taškų aibė sudarys spindulį AT. Taškų aibė Pt, kuri atitiks šio spindulio taškus, yra lankas l. Be to, taškas P(-pi/2) nepriklauso šiam lankui. TRIGONOMETRINĖS NELYGYBĖS SPRENDIMO METODAI
Aktualumas.
Istoriškai trigonometrinėms lygtims ir nelygybėms mokyklos programoje buvo skirta ypatinga vieta. Galima sakyti, kad trigonometrija yra viena iš svarbiausių mokyklos kurso ir apskritai viso matematikos mokslo dalių. Trigonometrinės lygtys ir nelygybės vidurinės mokyklos matematikos kurse užima vieną iš centrinių vietų tiek pagal mokomosios medžiagos turinį, tiek apie ugdomosios ir pažintinės veiklos metodus, kurie gali ir turėtų būti suformuoti jų studijų metu ir pritaikyti sprendžiant daug teorinio ir taikomojo pobūdžio problemų . Trigonometrinių lygčių ir nelygybių sprendimas sukuria prielaidas sisteminti mokinių žinias, susijusias su visa mokomąja medžiaga trigonometrijoje (pavyzdžiui, trigonometrinių funkcijų savybes, trigonometrinių išraiškų transformavimo būdus ir kt.) ir leidžia užmegzti efektyvius ryšius su studijuojama medžiaga. algebroje (lygtys, lygčių ekvivalentiškumas, nelygybės, identiškos algebrinių reiškinių transformacijos ir kt.). Kitaip tariant, trigonometrinių lygčių ir nelygybių sprendimo būdų svarstymas apima savotišką šių įgūdžių perkėlimą į naują turinį. Teorijos reikšmė ir daugybė jos pritaikymų yra pasirinktos temos aktualumo įrodymas. Tai savo ruožtu leidžia nustatyti kursinio darbo tikslus, uždavinius ir tyrimo dalyką. Tyrimo tikslas:
apibendrinti turimus trigonometrinių nelygybių tipus, pagrindinius ir specialiuosius jų sprendimo būdus, parinkti mokinių trigonometrinių nelygybių sprendimo uždavinių rinkinį. Tyrimo tikslai:
1. Remiantis turimos literatūros analize tiriama tema, susisteminti medžiagą. 2. Pateikite užduočių rinkinį, reikalingą temai „Trigonometrinės nelygybės“ konsoliduoti. Tyrimo objektas
yra trigonometrinės nelygybės mokykliniame matematikos kurse. Studijų dalykas:
trigonometrinių nelygybių rūšys ir jų sprendimo būdai. Teorinė reikšmė
yra sisteminti medžiagą. Praktinė reikšmė:
teorinių žinių taikymas sprendžiant problemas; pagrindinių bendrų trigonometrinių nelygybių sprendimo metodų analizė. Tyrimo metodai
: mokslinės literatūros analizė, įgytų žinių sintezė ir apibendrinimas, problemų sprendimo analizė, optimalių nelygybių sprendimo metodų paieška. §1.
Trigonometrinių nelygybių rūšys ir pagrindiniai jų sprendimo būdai
1.1. Paprasčiausios trigonometrinės nelygybės
Dvi trigonometrinės išraiškos, sujungtos ženklu arba >, vadinamos trigonometrinėmis nelygybėmis. Trigonometrinės nelygybės sprendimas reiškia nežinomųjų, įtrauktų į nelygybę, reikšmių rinkinį, kurio nelygybė tenkinama. Pagrindinė trigonometrinių nelygybių dalis išspręsta sumažinant jas iki paprasčiausio sprendimo: Tai gali būti faktorizavimo metodas, kintamojo ( Paprasčiausias nelygybes galima išspręsti dviem būdais: naudojant vienetų apskritimą arba grafiškai. Leistif(x
– viena pagrindinių trigonometrinių funkcijų. Norėdami išspręsti nelygybę Pateiksime nelygybių sprendimo algoritmo pavyzdį Nelygybės sprendimo algoritmas 1. Suformuluokite skaičiaus sinuso apibrėžimąx
ant vieneto apskritimo. 3. Ordinačių ašyje pažymėkite tašką koordinatea
.
4. Per šį tašką nubrėžkite tiesę, lygiagrečią OX ašiai, ir pažymėkite jos susikirtimo taškus su apskritimu. 5. Pasirinkite apskritimo lanką, kurio visų taškų ordinatės yra mažesnės uža
.
6. Nurodykite rato kryptį (prieš laikrodžio rodyklę) ir užrašykite atsakymą, įtraukdami funkcijos periodą prie intervalo galų.2πn
,
Nelygybės sprendimo algoritmas 1. Suformuluokite skaičiaus liestinės apibrėžimąx
ant vieneto apskritimo. 2. Nubrėžkite vienetinį apskritimą. 3. Nubrėžkite liestinių liniją ir pažymėkite joje tašką su ordinatėmisa
.
4. Sujunkite šį tašką su pradžios tašku ir pažymėkite gautos atkarpos susikirtimo tašką su vienetiniu apskritimu. 5. Pasirinkite apskritimo lanką, kurio visų taškų liestinės tiesės ordinatės yra mažesnės uža
.
6. Nurodykite važiavimo kryptį ir parašykite atsakymą atsižvelgdami į funkcijos apibrėžimo sritį, pridėdami tašką.πn
,
Paprasčiausių lygčių sprendinių grafinis aiškinimas ir nelygybių sprendimo formulės bendra forma nurodyta priede (1 ir 2 priedai). 1 pavyzdys.
Išspręskite nelygybę Nubrėžkite tiesią liniją ant vieneto apskritimo Visos reikšmėsy
intervale NM yra didesnis
, visi AMB lanko taškai tenkina šią nelygybę. Visais sukimosi kampais, didelis 1 pav Taigi, nelygybės sprendimas bus visos intervalo reikšmės tie. Atsakymas: 1.2. Grafinis metodas
Praktikoje grafinis trigonometrinių nelygybių sprendimo metodas dažnai pasirodo esąs naudingas. Panagrinėkime metodo esmę nelygybės pavyzdžiu 1. Jei argumentas yra sudėtingas (skirtingas nuoX
), tada pakeiskite jį įt
.
2. Statome vienoje koordinačių plokštumojetOy
funkcijų grafikai 3. Randame tokiusdu gretimi grafikų susikirtimo taškai, tarp kuriųsinusinės bangosesančiosaukštesnė
tiesiai 4. Argumentui parašykite dvigubą nelygybęt
, atsižvelgiant į kosinuso periodą (t
bus tarp rastų abscisių). 5. Atlikite atvirkštinį keitimą (grįžkite prie pradinio argumento) ir išreikškite reikšmęX
iš dvigubos nelygybės atsakymą rašome skaitinio intervalo forma. 2 pavyzdys.
Išspręskite nelygybę: . Sprendžiant nelygybes grafiniu metodu, būtina kuo tiksliau sukonstruoti funkcijų grafikus. Transformuokime nelygybę į formą: Sukurkime funkcijų grafikus vienoje koordinačių sistemoje 2 pav Funkcijų grafikai susikerta taškeA
su koordinatėmis Atsakymas: 1.3. Algebrinis metodas
Gana dažnai pradinė trigonometrinė nelygybė gali būti sumažinta iki algebrinės (racionalios arba neracionalios) nelygybės, naudojant gerai parinktą pakaitalą. Šis metodas apima nelygybės transformavimą, pakaitų įvedimą arba kintamojo pakeitimą. Pažvelkime į konkrečius šio metodo taikymo pavyzdžius. 3 pavyzdys.
Sumažinimas į paprasčiausią formą 3 pav Atsakymas: 4 pavyzdys.
Išspręskite nelygybę: ODZ: Naudojant formules: Parašykime nelygybę formoje: Arba, tikėdamas Išspręsdami paskutinę nelygybę intervalo metodu, gauname: 4 pav 5 pav Atsakymas: 1.4. Intervalinis metodas
Bendra trigonometrinių nelygybių sprendimo intervalo metodu schema: Koeficientas naudojant trigonometrines formules. Raskite funkcijos nepertraukiamumo taškus ir nulius ir padėkite juos ant apskritimo. Paimkite bet kurį taškąKAM
(bet anksčiau nerasta) ir išsiaiškinkite prekės ženklą. Jei sandauga teigiama, ant kampą atitinkančio spindulio už vienetinio apskritimo uždėkite tašką. Priešingu atveju įdėkite tašką apskritimo viduje. Jei taškas pasitaiko lyginį skaičių kartų, mes jį vadiname lyginio daugybos tašku, o jei nelyginį skaičių kartų, vadiname nelyginio daugybos tašku. Nubrėžkite lankus taip: pradėkite nuo taškoKAM
, jei kitas taškas yra nelyginio daugumo, tai lankas šiame taške kerta apskritimą, o jei taškas yra lyginio dauginio, tada jis nesikerta. Lankai už apskritimo yra teigiami intervalai; apskritimo viduje yra neigiamų erdvių. 5 pavyzdys.
Išspręskite nelygybę Pirmosios serijos taškai: Antrosios serijos taškai: Kiekvienas taškas pasitaiko nelyginį skaičių kartų, tai yra, visi taškai yra nelyginio daugumo. Sužinokime prekės ženklą adresu Ryžiai. 6 Atsakymas: 6 pavyzdys
. Išspręskite nelygybę.
Sprendimas:
Raskime išraiškos nulius .
Gautiaem :
Ant vieneto apskritimo serijos vertėsX
1
pavaizduoti taškais Leisk dabar skaičių Taigi, taškasA
turėtų būti parinktas ant spindulio, sudarančio kampą Dabar iš taškoA
nuosekliai nubrėžkite banguotą ištisinę liniją į visus pažymėtus taškus. Ir taškuose 7 pav Galutinis atsakymas: Pastaba.
Jei banguota linija, apėjus visus vienetinio apskritimo taškus, negali būti grąžinta į taškąA
,
neperžengus apskritimo „nelegalioje“ vietoje, tai reiškia, kad sprendime buvo padaryta klaida, būtent, praleistas nelyginis šaknų skaičius. Atsakymas:
.
§2. Trigonometrinių nelygybių sprendimo uždavinių rinkinys
Ugdant mokinių gebėjimą spręsti trigonometrines nelygybes, taip pat galima išskirti 3 etapus. 1. parengiamieji, 2. ugdyti gebėjimą spręsti paprastas trigonometrines nelygybes; 3. kitų tipų trigonometrinių nelygybių įvedimas. Parengiamojo etapo tikslas yra tai, kad moksleiviuose būtina ugdyti gebėjimą naudoti trigonometrinį apskritimą ar grafiką sprendžiant nelygybes, būtent: Gebėjimas spręsti paprastas formos nelygybes Gebėjimas sudaryti dvigubas nelygybes skaičių apskritimo lankams arba funkcijų grafikų lankams; Gebėjimas atlikti įvairias trigonometrinių išraiškų transformacijas. Šį etapą rekomenduojama įgyvendinti sisteminant moksleivių žinias apie trigonometrinių funkcijų savybes. Pagrindinės priemonės gali būti mokiniams siūlomos užduotys, atliekamos vadovaujant mokytojui arba savarankiškai, taip pat įgūdžiai, lavinami sprendžiant trigonometrines lygtis. Štai tokių užduočių pavyzdžiai: 1
. Pažymėkite tašką vieneto apskritime .
2.
Kuriame koordinačių plokštumos ketvirtyje yra taškas? 3.
Pažymėkite taškus trigonometriniame apskritime 4.
Konvertuoti išraišką į trigonometrines funkcijasašketvirčiai. A) 5.
Pateikiamas lanko MR.M
– vidurysaš– ketvirtį,R
– vidurysIIketvirtį. Apribokite kintamojo reikšmęt
už: (padarykite dvigubą nelygybę) a) lanko MR; b) RM lankai. 6.
Užrašykite pasirinktų grafiko dalių dvigubą nelygybę: Ryžiai. 1 7.
Išspręskite nelygybes 8.
Konvertuoti išraišką
.
Antrajame mokymosi spręsti trigonometrines nelygybes etape galime pasiūlyti šias rekomendacijas, susijusias su studentų veiklos organizavimo metodika. Šiuo atveju reikia sutelkti dėmesį į turimus mokinių darbo su trigonometriniu apskritimu ar grafiku įgūdžius, suformuotus sprendžiant paprasčiausias trigonometrines lygtis. Pirma, galima motyvuoti bendrąjį paprasčiausių trigonometrinių nelygybių sprendimo metodo gavimo tikslingumą, kreipiantis, pavyzdžiui, į formos nelygybę. Antra, mokytojas turėtų atkreipti mokinių dėmesį į skirtingus užduoties atlikimo būdus, pateikti tinkamą nelygybės sprendimo pavyzdį tiek grafiškai, tiek naudojant trigonometrinį apskritimą. Panagrinėkime šiuos nelygybės sprendimus 1. Nelygybės sprendimas naudojant vienetinį apskritimą. Pirmoje trigonometrinių nelygybių sprendimo pamokoje mokiniams pasiūlysime išsamų sprendimo algoritmą, kuris žingsnis po žingsnio pristatyme atspindi visus pagrindinius įgūdžius, reikalingus nelygybei išspręsti. 1 žingsnis.Nubrėžkime vienetinį apskritimą ir pažymime tašką ordinačių ašyje 2 žingsnis.Ši tiesi linija padalijo apskritimą į du lankus. Pasirinkime tą, kuriame pavaizduoti skaičiai, kurių sinusas didesnis už Ryžiai. 2 3 veiksmas.Pasirinkite vieną iš pažymėto lanko galų. Užrašykime vieną iš skaičių, kurį pavaizduoja šis vienetinio apskritimo taškas 4 veiksmas.Norėdami pasirinkti skaičių, atitinkantį antrąjį pasirinkto lanko galą, mes „einame“ šiuo lanku nuo pavadinto galo iki kito. Tuo pačiu atminkite, kad judant prieš laikrodžio rodyklę, skaičiai, kuriais eisime, didėja (judant priešinga kryptimi skaičiai mažėtų). Užrašykime skaičių, kuris pavaizduotas vieneto apskritime iki antrojo pažymėto lanko galo Taigi matome tą nelygybę Mokinių turėtų būti paprašyta atidžiai išnagrinėti piešinį ir išsiaiškinti, kodėl visi nelygybės sprendimai Ryžiai. 3 Būtina atkreipti mokinių dėmesį į tai, kad spręsdami kosinuso funkcijos nelygybes brėžiame lygiagrečią ordinačių ašiai tiesę. Grafinis nelygybių sprendimo metodas. Kuriame grafikus Ryžiai. 4 Tada parašome lygtį (Duotin
reikšmes 0, 1, 2, randame tris sudarytos lygties šaknis). Vertybės Ryžiai. 5 Apibendrinti. Norėdami išspręsti nelygybę Trečia, faktas apie atitinkamos trigonometrinės nelygybės šaknų aibę labai aiškiai pasitvirtina ją sprendžiant grafiškai. Ryžiai. 6 Būtina parodyti studentams, kad posūkis, kuris yra nelygybės sprendimas, kartojasi per tą patį intervalą, lygų trigonometrinės funkcijos periodui. Taip pat galite apsvarstyti panašią sinusinės funkcijos grafiko iliustraciją. Ketvirta, patartina atlikti darbą atnaujinant studentų metodus, kaip trigonometrinių funkcijų sumą (skirtumą) paversti sandauga, ir atkreipti studentų dėmesį į šių metodų vaidmenį sprendžiant trigonometrines nelygybes. Toks darbas gali būti organizuojamas mokiniams savarankiškai atliekant mokytojo pasiūlytas užduotis, tarp kurių išskiriame: Penkta, studentai turi iliustruoti kiekvienos paprastos trigonometrinės nelygybės sprendimą, naudodami grafiką arba trigonometrinį apskritimą. Būtinai turėtumėte atkreipti dėmesį į jo tikslingumą, ypač į apskritimo naudojimą, nes sprendžiant trigonometrines nelygybes, atitinkama iliustracija yra labai patogi priemonė įrašyti tam tikros nelygybės sprendinių rinkinį. Patartina supažindinti studentus su ne pačiais paprasčiausiais trigonometrinių nelygybių sprendimo būdais pagal šią schemą: pereinant prie konkrečios trigonometrinės nelygybės, pereinant prie atitinkamos trigonometrinės lygties bendros paieškos (dėstytojas – studentai) sprendinio nepriklausomas perkėlimas. rastas metodas kitoms to paties tipo nelygybėms. Norint susisteminti studentų žinias apie trigonometriją, rekomenduojame specialiai atrinkti tokias nelygybes, kurių sprendimas reikalauja įvairių transformacijų, kurias galima įgyvendinti sprendžiant, ir sutelkti studentų dėmesį į jų ypatybes. Kaip tokias produktyvias nelygybes galime pasiūlyti, pavyzdžiui: Pabaigoje pateikiame trigonometrinių nelygybių sprendimo uždavinių rinkinio pavyzdį. 1. Išspręskite nelygybes: A) b) 5. Raskite visus nelygybių sprendimus: A) ;
b) ;
V) G) d) 6. Išspręskite nelygybes: A) ;
b) ;
V); G) d) ; e) ; ir) 7. Išspręskite nelygybes: A) b) ;
V); G) . 8. Išspręskite nelygybes: A) ;
b) ;
V); G) d) e) ; ir) h) . 6 ir 7 užduotis patartina siūlyti matematiką aukštesniuoju lygiu studijuojantiems studentams, 8 užduotį – aukštesnio lygio matematikos studijų klasių mokiniams. §3. Specialūs trigonometrinių nelygybių sprendimo metodai
Specialūs trigonometrinių lygčių sprendimo metodai – tai yra tie metodai, kurie gali būti naudojami tik trigonometrinėms lygtims spręsti. Šie metodai yra pagrįsti trigonometrinių funkcijų savybių naudojimu, taip pat įvairių trigonometrinių formulių ir tapatybių naudojimu. 3.1. Sektorinis metodas
Panagrinėkime sektorių metodą trigonometrinėms nelygybėms spręsti. Formos nelygybių sprendimas Intervaliniu metodu kiekvienas formos skaitiklio ir vardiklio tiesinis koeficientas Reikia atsiminti šiuos dalykus: a) Formos veiksniai b) Formos veiksniai 1 pavyzdys.
Išspręskite nelygybes: a) 3.2. Koncentrinio apskritimo metodas
Šis metodas yra lygiagrečių skaičių ašių metodo analogas racionaliųjų nelygybių sistemoms spręsti. Panagrinėkime nelygybių sistemos pavyzdį. 5 pavyzdys.
Išspręskite paprastų trigonometrinių nelygybių sistemą Pirmiausia kiekvieną nelygybę išsprendžiame atskirai (5 pav.). Viršutiniame dešiniajame paveikslo kampe nurodysime, kuriam argumentui svarstomas trigonometrinis apskritimas. 5 pav Toliau mes sukuriame argumento koncentrinių apskritimų sistemąX
. Nubrėžiame apskritimą ir nuspalviname jį pagal pirmosios nelygybės sprendinį, tada nubrėžiame didesnio spindulio apskritimą ir nuspalviname jį pagal antrosios sprendinį, tada konstruojame apskritimą trečiajai nelygybei ir pagrindo apskritimą. Mes ištraukiame spindulius iš sistemos centro per lankų galus taip, kad jie kirstų visus apskritimus. Ant pagrindo apskritimo formuojame tirpalą (6 pav.). 6 pav Atsakymas:
Išvada
Visi kurso tyrimo tikslai buvo įgyvendinti. Susisteminta teorinė medžiaga: pateikiami pagrindiniai trigonometrinių nelygybių tipai ir pagrindiniai jų sprendimo būdai (grafinis, algebrinis, intervalų metodas, sektoriai ir koncentrinių apskritimų metodas). Kiekvienam metodui buvo pateiktas nelygybės sprendimo pavyzdys. Po teorinės dalies sekė praktinė dalis. Jame yra užduočių rinkinys trigonometrinėms nelygybėms spręsti. Šį kursinį darbą studentai gali naudoti savarankiškam darbui. Mokiniai gali pasitikrinti šios temos įvaldymo lygį ir praktikuotis atliekant įvairaus sudėtingumo užduotis. Išstudijavus aktualią literatūrą šia tema, akivaizdžiai galime daryti išvadą, kad mokyklinio algebros ir elementarios analizės kurse labai svarbūs gebėjimai ir įgūdžiai spręsti trigonometrines nelygybes, kurių plėtojimas reikalauja didelių matematikos mokytojo pastangų. Todėl šis darbas bus naudingas matematikos mokytojams, nes leidžia efektyviai organizuoti mokinių mokymą tema „Trigonometrinės nelygybės“. Tyrimą galima tęsti išplečiant jį iki galutinio kvalifikacinio darbo.
Naudotos literatūros sąrašas
Bogomolovas, N.V. Matematikos uždavinių rinkinys [Tekstas] / N.V. Bogomolovas. – M.: Bustard, 2009. – 206 p. Vygodskis, M.Ya. Elementariosios matematikos vadovas [Tekstas] / M.Ya. Vygodskis. – M.: Bustard, 2006. – 509 p. Žurbenko, L.N. Matematika pavyzdžiuose ir uždaviniuose [Tekstas] / L.N. Žurbenko. – M.: Infra-M, 2009. – 373 p. Ivanovas, O.A. Elementarioji matematika moksleiviams, studentams ir mokytojams [Tekstas] / O.A. Ivanovas. – M.: MTsNMO, 2009. – 384 p. Karpas, A.P. Algebros užduotys ir analizės pradžia organizuojant galutinį kartojimą ir atestavimą 11 klasėje [Tekstas] / A.P. Karpis. – M.: Švietimas, 2005. – 79 p. Kulaninas, E.D. 3000 matematikos konkursinių uždavinių [Tekstas] / E.D. Kulaninas. – M.: Iris-press, 2007. – 624 p. Leibsonas, K.L. Praktinių matematikos užduočių rinkinys [Tekstas] / K.L. Leibsonas. – M.: Bustard, 2010. – 182 p. Alkūnė, V.V. Problemos su parametrais ir jų sprendimas. Trigonometrija: lygtys, nelygybės, sistemos. 10 klasė [Tekstas] / V.V. Alkūnė. – M.: ARKTI, 2008. – 64 p. Manova, A.N. Matematika. Greitasis dėstytojas ruošiantis vieningam valstybiniam egzaminui: studentas. vadovas [tekstas] / A.N. Manova. – Rostovas prie Dono: Feniksas, 2012. – 541 p. Mordkovičius, A.G. Algebra ir matematinės analizės pradžia. 10-11 klasių. Vadovėlis bendrojo ugdymo įstaigų mokiniams [Tekstas] / A.G. Mordkovičius. – M.: Iris-press, 2009. – 201 p. Novikovas, A.I. Trigonometrinės funkcijos, lygtys ir nelygybės [Tekstas] / A.I. Novikovas. – M.: FIZMATLIT, 2010. – 260 p. Oganesjanas, V.A. Matematikos mokymo metodai vidurinėje mokykloje: Bendroji metodika. Vadovėlis vadovas fizikos studentams - mat. fak. ped. Inst. [Tekstas] / V.A. Oganesjanas. – M.: Švietimas, 2006. – 368 p. Olehnikas, S.N. Lygtys ir nelygybės. Nestandartiniai sprendimo būdai [Tekstas] / S.N. Olehnik. – M.: Factorial leidykla, 1997. – 219 p. Sevryukovas, P.F. Trigonometrinės, eksponentinės ir logaritminės lygtys ir nelygybės [Tekstas] / P.F. Sevriukovas. – M.: Visuomenės švietimas, 2008. – 352 p. Sergejevas, I. N. Vieningas valstybinis egzaminas: 1000 matematikos uždavinių su atsakymais ir sprendimais. Visos C grupės užduotys [Tekstas] / I.N. Sergejevas. – M.: Egzaminas, 2012. – 301 p. Sobolevas, A.B. Elementarioji matematika [Tekstas] / A.B. Sobolevas. – Jekaterinburgas: Valstybinė aukštojo profesinio mokymo įstaiga USTU-UPI, 2005. – 81 p. Fenko, L.M. Intervalų metodas sprendžiant nelygybes ir tiriant funkcijas [Tekstas] / L.M. Fenko. – M.: Bustard, 2005. – 124 p. Friedmanas, L.M. Teoriniai matematikos mokymo metodų pagrindai [Tekstas] / L.M. Friedmanas. – M.: Knygų namai „LIBROKOM“, 2009. – 248 p. 1 priedas Paprastų nelygybių sprendinių grafinė interpretacija Ryžiai. 1 Ryžiai. 2 3 pav 4 pav 5 pav 6 pav 7 pav 8 pav 2 priedas Paprastų nelygybių sprendimai
, 
ir tt), kur pirmiausia išsprendžiama įprasta nelygybė, o po to – formos nelygybė 
ir tt, ar kitais būdais.
jos sprendimą pakanka rasti vienu periodu, t.y. bet kuriame segmente, kurio ilgis lygus funkcijos perioduif
x
. Tada bus rastas pirminės nelygybės sprendimasx
, taip pat tos reikšmės, kurios skiriasi nuo tų, kurias randa bet koks sveikasis funkcijos periodų skaičius. Šiuo atveju patogu naudoti grafinį metodą.
(
) Ir 
.
(
).
.
.
(skaičius įrašo kairėje visada yra mažesnis už skaičių dešinėje).
.
, kuris kerta apskritimą taškuose A ir B.
, bet mažesnis 
,
perims didesnes vertybes
(bet ne daugiau kaip vieną).
, t.y. 
. Norint gauti visus šios nelygybės sprendinius, pakanka pridėti prie šio intervalo galų 
, Kur 
, t.y. 
,
.
Atkreipkite dėmesį, kad vertės 
Ir 
yra lygties šaknys 
,
;
.
, .
:
Ir 
.
. Randame šių taškų abscises.
Ir 
(2 pav.).
; 
. Tarp 
grafiko taškai 
žemiau grafiko taškų 
. Ir kada funkcijų reikšmės yra vienodos. Štai kodėl adresu 
.
.
.
(3 pav.)
, 
.
, 
, 
.
, 
.
po paprastų transformacijų gauname
,
,
.
, atitinkamai 
. Tada iš fig. 4 seka 
, Kur 
.
, 
.
, 
.
.
.
: . Vienetiniame apskritime pažymėkime visus taškus (6 pav.):
, 
; 
, 
; 
, 
.
,
;
, 
;
, 
;
, 
;
. SerijaX
2
suteikia taškų 
. SerijosX
3
gauname du taškus 
. Pagaliau serialasX
4
atstovaus taškus 
. Nubraižykime visus šiuos taškus vieneto apskritime, šalia kiekvieno skliausteliuose nurodydami jo daugumą.
bus lygus. Apskaičiuokime pagal ženklą:
su sijaOi,
už vieneto rato ribų. (Atkreipkite dėmesį, kad pagalbinė sijaAPIE
A
Visai nebūtina to pavaizduoti paveikslėlyje. TaškasA
parenkamas apytiksliai.)mūsų linija eina iš vienos srities į kitą: jei ji buvo už vieneto apskritimo ribų, tada ji eina jos viduje. Artėjant prie taško 
, linija grįžta į vidinę sritį, nes šio taško daugyba yra lyginė. Panašiai ir taške 
(su net daugybe) linija turi būti pasukta į išorinę sritį. Taigi, nupiešėme tam tikrą paveikslėlį, parodytą Fig. 7. Tai padeda paryškinti norimas sritis ant vieneto apskritimo. Jie pažymėti „+“ ženklu.
,
, ,
,
naudojant sinuso ir kosinuso funkcijų savybes;
, Jei, Jei 
lygus: 
, Jei:
,
b) 
,
V) 
, 
, 
, 
.
.
Pasinaudodami parengiamajame etape įgytomis žiniomis ir įgūdžiais, studentai pasiūlytą nelygybę įneš į formą 
, tačiau gali būti sunku rasti susidariusios nelygybės sprendimų rinkinį, nes Neįmanoma to išspręsti tik naudojant sinusinės funkcijos savybes. Šio sunkumo galima išvengti atsivertus atitinkamą iliustraciją (išsprendžiant lygtį grafiškai arba naudojant vienetinį apskritimą)..
ir per ją nubrėžkite tiesią liniją, lygiagrečią x ašiai. Ši linija susikirs su vieneto apskritimu dviejuose taškuose. Kiekvienas iš šių taškų reiškia skaičius, kurių sinusas yra lygus .
. Natūralu, kad šis lankas yra virš nubrėžtos tiesios linijos.
.
.
patenkinti skaičius, kuriems nelygybė yra teisinga 
. Išsprendėme skaičių, esančių tame pačiame sinusinės funkcijos periode, nelygybę. Todėl visi nelygybės sprendiniai gali būti parašyti forma 
galima parašyti formoje 
, 
.
Ir 
, turint omenyje 
.
ir jo sprendimas 
, 
, 
, rasta naudojant formules 
, 
, 
.
yra trys iš eilės einančios grafikų susikirtimo taškų abscisės Ir . Aišku, visada per intervalą 
nelygybė galioja 
, ir intervale 
– nelygybė 
. Mus domina pirmasis atvejis, o tada prie šio intervalo galų pridėjus skaičių, kuris yra sinuso periodo kartotinis, gauname nelygybės sprendimą kaip: 
, .
, reikia sukurti atitinkamą lygtį ir ją išspręsti. Iš gautos formulės raskite šaknis 
Ir 
, ir atsakymą į nelygybę parašykite tokia forma: , .
, tenkinantis sąlygą 
;
, tenkinantis sąlygą 
.
;
;
.
;
.
;
;
;
;
, KurP
(
x
)
IrK
(
x
)
– racionalios trigonometrinės funkcijos (į jas racionaliai įtraukiami sinusai, kosinusai, liestinės ir kotangentai), panašiai kaip sprendžiant racionaliąsias nelygybes. Racionaliąsias nelygybes patogu spręsti naudojant intervalų skaičių tiesėje metodą. Jo analogas racionalioms trigonometrinėms nelygybėms spręsti yra trigonometrinio apskritimo sektorių metodas,sinx
Ircosx
(
) arba trigonometrinis puslankistgx
Irctgx
(
).
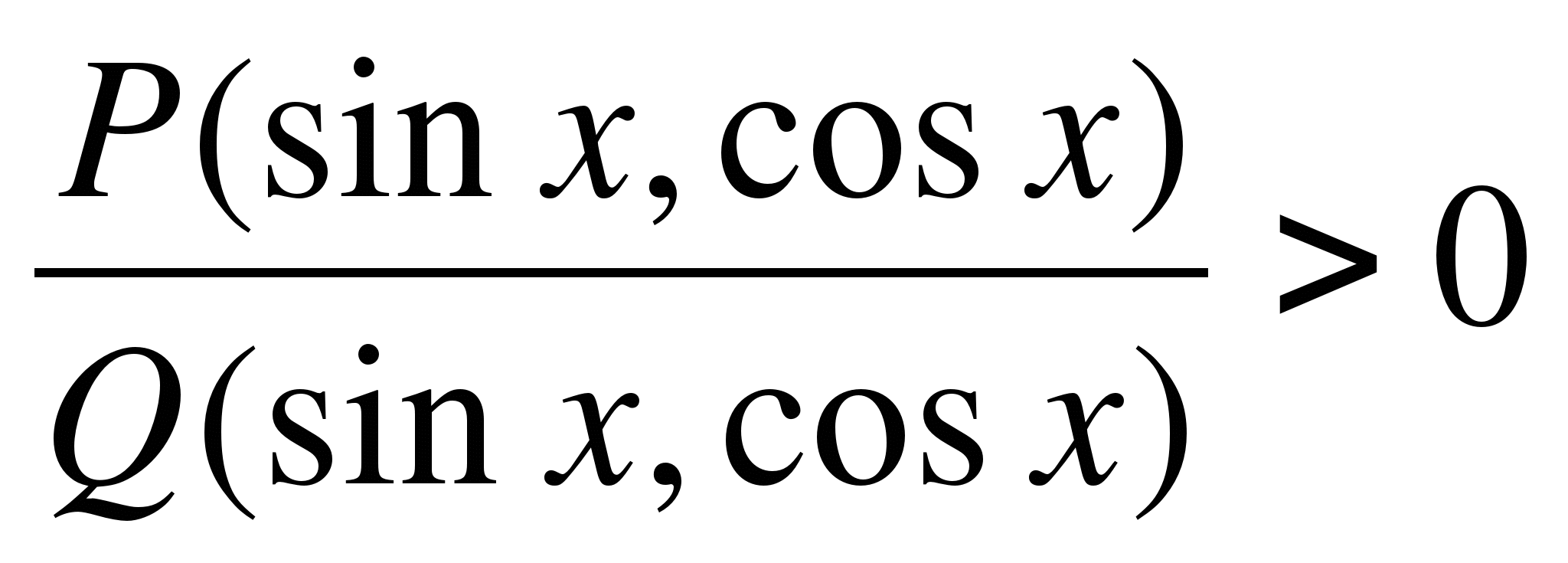
skaičių ašyje atitinka tašką 
, o einant per šį tašką keičia ženklą. Sektoriaus metodu kiekvienas formos veiksnys 
, Kur 
- viena iš funkcijųsinx
arbacosx
Ir 
, trigonometriniame apskritime atitinka du kampai 
Ir 
, kurie padalija apskritimą į du sektorius. Pravažiuojant Ir funkcija keičia ženklą.
Ir 
, Kur 
, išsaugokite ženklą visoms reikšmėms 
. Tokie skaitiklio ir vardiklio veiksniai atmetami keičiant (jei 
) su kiekvienu tokiu atmetimu nelygybės ženklas apverčiamas.
Ir 
taip pat išmesti. Be to, jei tai yra vardiklio veiksniai, tada formos nelygybės pridedamos prie ekvivalentinės nelygybių sistemos 
Ir 
. Jei tai yra skaitiklio veiksniai, tai ekvivalentinėje apribojimų sistemoje jie atitinka nelygybes Ir esant griežtai pradinei nelygybei ir lygybei 
Ir 
esant negriežtai pradinei nelygybei. Atmetus daugiklį 
arba 
nelygybės ženklas yra apverstas.
, b) 
.
turime funkciją b) . Išspręskite mūsų turimą nelygybę,
, 
.
