വിഭാഗങ്ങളുടെ നിർമ്മാണം. "പോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ" എന്ന വിഷയത്തെക്കുറിച്ചുള്ള ഗവേഷണ പ്രവർത്തനങ്ങൾ

29.09.2019

മുമ്പത്തെ ജോലികളിൽ, ക്രോസ്-സെക്ഷൻ നിർമ്മിക്കാൻ ഞങ്ങൾക്ക് സിദ്ധാന്തത്തെക്കുറിച്ചുള്ള അറിവ് മതിയായിരുന്നു. നമുക്ക് മറ്റൊരു പ്രശ്നം പരിഗണിക്കാം. ടാസ്ക് 1. ABD വിമാനത്തിന് സമാന്തരമായി പോയിൻ്റ് M വഴി കടന്നുപോകുന്ന ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക. എം ഒരു പോയിൻ്റ് ഞങ്ങളെ ഒരു തരത്തിലും സഹായിക്കില്ല, പക്ഷേ പ്രശ്നത്തിന് ഒരു അധിക വ്യവസ്ഥയുണ്ട്: വിഭാഗം വിമാനം എബിഡിക്ക് സമാന്തരമായിരിക്കണം. ഇത് നമുക്ക് എന്താണ് നൽകുന്നത്? 1. എഡിബിയും ഡിബിസിയും നേർരേഖയായ ഡിബിയിൽ കൂടിച്ചേരുന്നു, അതിനാൽ എഡിബിക്ക് സമാന്തരമായ ഒരു വിഭാഗം ഡിബിസിയെ വിഭജിക്കുന്നു (ഡിബിക്ക് സമാന്തരമായ രണ്ട് സമാന്തര നേർരേഖകൾ മൂന്നിലൊന്ന് വിഭജിക്കുകയാണെങ്കിൽ, വിഭജനത്തിൻ്റെ രേഖകൾ സമാന്തരമാണ്) എം പോയിൻ്റ് എം ഉൾപ്പെടുന്നു. ഡിബിസിയെ നേരിടാൻ. നമുക്ക് അതിലൂടെ DB-ക്ക് സമാന്തരമായ MK എന്ന നേർരേഖ വരയ്ക്കാം. 2. അതുപോലെ: (ADB) (ABC)=AB, K ആയതിനാൽ AB ന് സമാന്തരമായി ഒരു നേർരേഖയിൽ ഈ വിഭാഗം (ABC) വിഭജിക്കും. കെ(എബിസി). ABC എന്ന തലത്തിലെ പോയിൻ്റ് K വഴി AB ന് സമാന്തരമായി KN എന്ന നേർരേഖ വരയ്ക്കുക. എം എൻ കെ എൻ (എഡിസി), എം (എഡിസി), അതിനാൽ എംഎൻ (എഡിസി) (ഒപ്പം കട്ടിംഗ് വിമാനങ്ങളും). NM നടത്താം. MKN ആണ് ആവശ്യമുള്ള വിഭാഗം. അതിനാൽ: M N 1. നിർമ്മാണം: 1. വിമാനത്തിൽ (DBC) MK // DB, MK BC = K. 2. വിമാനത്തിൽ (ABC) KN // AB, KN AC = N. 3. MN അത് തെളിയിക്കാം MKN ആണ് ആവശ്യമുള്ള വിഭാഗം K 2. തെളിവ്. 1. വിഭാഗം M 2. N (ADC), M (ADC) => NM (ADC) 3. MK // DB, NK // AB എന്ന പോയിൻ്റിലൂടെ കടന്നുപോകുന്നു, അതിനാൽ (NMK) // (ABD) വഴി ആട്രിബ്യൂട്ട്. അതിനാൽ, B.t.c-യുടെ ആവശ്യമുള്ള വിഭാഗമാണ് MKN. പ്രശ്നം 2. എഡ്ജ് D1C1 ൻ്റെയും പോയിൻ്റ് Dയുടെയും മധ്യത്തിലൂടെ കടന്നുപോകുന്ന സമാന്തരപൈപ്പുള്ള ABCDA1B1C1D1 ൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക, a നേർരേഖയ്ക്ക് സമാന്തരമായി. B1 C1 ന്യായവാദം. M A1 D1 B A C D 1. വ്യവസ്ഥയിൽ സൂചിപ്പിച്ചിരിക്കുന്ന പോയിൻ്റ് അടയാളപ്പെടുത്തുക (നമുക്ക് അതിനെ ഏകപക്ഷീയമായി വിളിക്കാം). M - D1C1 ൻ്റെ മധ്യഭാഗം. 2. പോയിൻ്റുകൾ M, D നുണ B1 C1 M A1 A, അതായത് അവയെ ബന്ധിപ്പിക്കാൻ കഴിയും. D1 B C D അതേ വിമാനത്തിൽ DD1C1, കണക്റ്റുചെയ്യാൻ കൂടുതലൊന്നുമില്ല. 3. നമുക്ക് ഒരു അധിക വ്യവസ്ഥ ഉപയോഗിക്കാം: കട്ടിംഗ് വിമാനം നേർരേഖയ്ക്ക് സമാന്തരമായിരിക്കണം a. B1 C1 M A1 B C S A ഇത് ചെയ്യുന്നതിന്, അതിൽ a വരിയ്ക്ക് സമാന്തരമായ ഒരു ലൈൻ ഉണ്ടായിരിക്കണം. എബിസി വിമാനത്തിൽ അത്തരമൊരു നേർരേഖ വരയ്ക്കുക എന്നതാണ് ഏറ്റവും എളുപ്പമുള്ള മാർഗം, കാരണം അതിൽ ഒരു നേർരേഖ a, വിഭാഗത്തിൽപ്പെട്ട ഒരു പോയിൻ്റ് D എന്നിവ അടങ്ങിയിരിക്കുന്നു. D ABC പ്ലെയിനിൽ, പോയിൻ്റ് D വഴി, a നേർരേഖയ്ക്ക് സമാന്തരമായി DS ഒരു നേർരേഖ വരയ്ക്കുക. DS AB = S. 4. കാരണം (ABC) // (A1B1C1), പ്ലെയിനിൽ വരയ്ക്കുക (A1B1C1), പോയിൻ്റ് M വഴി, ലൈൻ MP // SD. MP B1C1 = P 5. കാരണം (DD1C1) // (AA1B1), തുടർന്ന് P B C തലത്തിൽ (AA1B1) പോയിൻ്റ് S വഴി നമുക്ക് DM-ന് സമാന്തരമായി M N A D SN എന്ന നേർരേഖ വരയ്ക്കാം. SN BB1 = N 1 1 1 1 B C S A D 6. N, P പോയിൻ്റുകൾ വിമാനത്തിൽ കിടക്കുന്നു (A1B1C1). നമുക്ക് അവരെ ബന്ധിപ്പിക്കാം. SNPMD - ആവശ്യമായ വിഭാഗം. അതിനാൽ: 1. നിർമ്മാണം. 1. MD B1 A1 N P C1 S A M 3. ഇൻ (A1B1C1), പോയിൻ്റ് M, MP // DS, MP B1C1 = P C 4 എന്നിവയിലൂടെ. വിമാനത്തിൽ (AA1B1), പോയിൻ്റ് S, SN // DM, SN BB1 = N 5. NP D1 B D 2. ഇൻ (ABC), പോയിൻ്റ് D, DS // a, DS AB = S എന്ന പോയിൻ്റിലൂടെ SNPMD എന്ന് നമുക്ക് തെളിയിക്കാം. ആവശ്യമുള്ള വിഭാഗമാണ്. 2. തെളിവ്. ബി. P C1 M C S A 3. PM // SD, P B1C1 നിർമ്മാണത്തിലൂടെ D1 B D 2. DS // a, (S AB) നിർമ്മാണത്തിലൂടെ, അതിനാൽ (KNP) // a ആട്രിബ്യൂട്ട് പ്രകാരം. 4. SN // DM, N BB1 നിർമ്മാണത്തിലൂടെ 5. P (BB1C1), N (BB1C1) => PN (BB1C1). അതിനാൽ, SNPMD എന്നത് ആവശ്യമുള്ള ക്രോസ് സെക്ഷൻ മുതലായവയാണ്. പ്രശ്നം 3. B1A യ്ക്ക് സമാന്തരമായി സമാന്തരമായി ഒരു സമാന്തരപൈപ്പിൻ്റെ ഒരു വിഭാഗം നിർമ്മിക്കുക, പോയിൻ്റ് M, N എന്നിവയിലൂടെ കടന്നുപോകുക. 1. M, N എന്നിവ ബന്ധിപ്പിക്കുക (അവ വിമാനത്തിൽ കിടക്കുന്നു (C1A1B1)). B1 N M A1 D1 B A C1 C D കണക്റ്റുചെയ്യാൻ കൂടുതലൊന്നുമില്ല. നമുക്ക് ഒരു അധിക വ്യവസ്ഥ ഉപയോഗിക്കാം: കട്ടിംഗ് പ്ലെയിൻ ലൈൻ B1A 2 ന് സമാന്തരമായിരിക്കണം. കട്ടിംഗ് പ്ലെയിൻ AB1 ന് സമാന്തരമാകണമെങ്കിൽ, അതിൽ AB1 (അല്ലെങ്കിൽ DC1, മുതൽ DC // AB1 ന്) സമാന്തരമായ ഒരു ലൈൻ അടങ്ങിയിരിക്കേണ്ടത് ആവശ്യമാണ്. ഒരു സമാന്തര പൈപ്പിൻ്റെ സ്വത്ത്). DD1C1C മുഖത്ത് അത്തരമൊരു നേർരേഖ ചിത്രീകരിക്കുന്നത് ഏറ്റവും സൗകര്യപ്രദമാണ്, കാരണം (DD1C1) // (AA1B1), കൂടാതെ AB1 (AA1B1). നമുക്ക് പ്ലെയിനിൽ NK // AB1, NK DD1 = K എന്ന രേഖ വരയ്ക്കാം (DD1C1) B1 N M A1 D1 B 3. ഇപ്പോൾ AA1D1 വിമാനത്തിൽ വിഭാഗത്തിൽ പെട്ട M, K എന്നീ രണ്ട് പോയിൻ്റുകളുണ്ട്. നമുക്ക് അവരെ ബന്ധിപ്പിക്കാം. C K A C1 D MNK - ആവശ്യമായ വിഭാഗം. അതിനാൽ: 1. നിർമ്മാണം. 1. MN 2. വിമാനത്തിൽ (DD1C1) NK // AB1, NK DD1 = K. . B1 N A1 A M D1 C1 3. MK MNK ആണ് ആവശ്യമുള്ള വിഭാഗം എന്ന് നമുക്ക് തെളിയിക്കാം 2. തെളിവ്. B C 1. വിഭാഗം M, N. K എന്നീ പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്നു. M (A1B1C1), N (A1B1C1) => D MN (A1B1C1). 3. M (ADD1), K (ADD1) => MK (ADD1). 4. കാരണം നിർമ്മാണത്തിലൂടെ NK // AB1, പിന്നെ (MNK) // AB1 ഒരു ലൈനിൻ്റെയും ഒരു വിമാനത്തിൻ്റെയും സമാന്തരതയാൽ. അതിനാൽ, B.t.c. യുടെ ആവശ്യമുള്ള വിഭാഗമാണ് MNK. ടാസ്‌ക് 3. 1. ടെട്രാഹെഡ്രോൺ ഡിഎബിസിയിൽ, എഡ്ജ് ഡിസി, വെർട്ടെക്സ് ബി എന്നിവയുടെ മധ്യത്തിലൂടെയും ലൈൻ എസിക്ക് സമാന്തരമായും ഒരു തലം കടന്നുപോകുന്ന ഒരു ഭാഗം നിർമ്മിക്കുക. 2. B1C1 എന്ന എഡ്ജിൻ്റെ നടുവിലൂടെ ഒരു തലം കടന്നുപോകുന്ന ഒരു സമാന്തരപൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക, DK ആണെങ്കിൽ, BD രേഖയ്ക്ക് സമാന്തരമായി എഡ്ജ് CD-യിൽ കിടക്കുന്ന പോയിൻ്റ് K: KC = 1: 3. M 3. ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക. എം, സി പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം, സമാന്തരമായി a (ചിത്രം 1). ചിത്രം 1 4. സമാന്തര പൈപ്പ് ഉള്ള ABCDA1B1C1D1-ൽ, പോയിൻ്റ് E എഡ്ജ് സിഡിയിൽ പെടുന്നു. ഈ പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു വിമാനം ഉപയോഗിച്ച് സമാന്തര പൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക വിമാനത്തിന് സമാന്തരമായി BC1D. 5. MN ന് സമാന്തരമായി AA1 ലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് സമാന്തരപൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക, ഇവിടെ M എന്നത് AB യുടെ മധ്യബിന്ദുവാണ്, N എന്നത് BC യുടെ മധ്യബിന്ദുവാണ്. 6. AA1C1 വിമാനത്തിന് സമാന്തരമായി B1C1 എഡ്ജിൻ്റെ മധ്യത്തിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് സമാന്തരപൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക.

വിദ്യാഭ്യാസ മന്ത്രാലയം, ശാസ്ത്രംറിപ്പബ്ലിക് ഓഫ് ക്രൈമിലെ യുവജനങ്ങളും

സ്മോൾ അക്കാദമി ഓഫ് സയൻസസ് "സീക്കർ"

വകുപ്പ്: ഗണിതം

വിഭാഗം: ഗണിതം

പോളിഹെഡ്രോണുകളുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ

ഞാൻ ജോലി ചെയ്തു:

_______________

ക്ലാസ് വിദ്യാർത്ഥി

ശാസ്ത്ര ഉപദേഷ്ടാവ്:

സംഗ്രഹങ്ങൾ

പോളിഹെഡ്രയുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ

വകുപ്പ്: ഗണിതം

വിഭാഗം: ഗണിതം

ശാസ്ത്ര ഉപദേഷ്ടാവ്:

പഠനത്തിൻ്റെ ഉദ്ദേശ്യം പോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള വിവിധ രീതികളെക്കുറിച്ചുള്ള പഠനം. ഇതിനായി ഒപ്പംഈ വിഷയത്തെക്കുറിച്ചുള്ള സൈദ്ധാന്തിക മെറ്റീരിയൽ പഠിച്ചു, വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിലെ പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ ചിട്ടപ്പെടുത്തിയിരിക്കുന്നു, ഓരോ രീതിയുടെയും പ്രയോഗത്തിലെ പ്രശ്നങ്ങളുടെ ഉദാഹരണങ്ങൾ നൽകിയിരിക്കുന്നു, വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിലും അവയുടെ ഘടകങ്ങൾ കണക്കാക്കുന്നതിലും ഏകീകൃത സംസ്ഥാന പരീക്ഷയിലെ പ്രശ്നങ്ങളുടെ ഉദാഹരണങ്ങൾ പരിഗണിക്കുന്നു.

ആമുഖം …………………………………………………………………………………….3

വിഭാഗം 1. സീറോമെട്രിയുടെ ആക്‌സിയോം സിസ്റ്റത്തെ അടിസ്ഥാനമാക്കിയുള്ള പോളിഹെഡ്രോണുകളുടെ വിഭാഗങ്ങളുടെ നിർമ്മാണം.

വിഭാഗം 2. പോളിഹെഡ്രോണുകളുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള ട്രെയ്സ് രീതി …………………………………………………………………………………………………………

വിഭാഗം 3. ഇൻ്റേണൽ ഡിസൈൻ രീതി

പോളിഹെഡുകളുടെ വിഭാഗങ്ങളുടെ നിർമ്മാണത്തിൽ ………………………………14

വിഭാഗം 4. വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള സംയോജിത രീതി

പോളിഹെഡ്ര………………………………………………………… 17

വിഭാഗം 5. പോളിഹെഡുകളുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള കോർഡിനേറ്റ് രീതി …………………………………………………………………………………….

ഉപസംഹാരം ……………………………………………………………… 25

റഫറൻസുകൾ …………………………………………………… 26

ആമുഖം

ബിരുദധാരികൾക്ക് ഗണിതശാസ്ത്രത്തിൽ പരീക്ഷ എഴുതേണ്ടിവരും, സ്റ്റീരിയോമെട്രിക് പ്രശ്നങ്ങൾ പരിഹരിക്കാനുള്ള അറിവും കഴിവും ക്രമത്തിൽ ആവശ്യമാണ്, ഈ പരീക്ഷ എഴുതാൻപരമാവധി പോയിൻ്റുകൾ. പ്രസക്തി പരീക്ഷയ്ക്ക് സ്വതന്ത്രമായി തയ്യാറെടുക്കേണ്ടതിൻ്റെ ആവശ്യകത ഈ സൃഷ്ടിയിൽ ഉൾപ്പെടുന്നു, കൂടാതെ പരിഗണനയിലുള്ള വിഷയം ഏറ്റവും പ്രധാനപ്പെട്ട ഒന്നാണ്.

എ ഡെമോയുടെ വിശകലനം, രോഗനിർണയവും പരിശീലനവും ഏകീകൃത സംസ്ഥാന പരീക്ഷ ഓപ്ഷനുകൾകൂടെ 2009-2014 അത് 70% കാണിച്ചു ജ്യാമിതീയ ജോലികൾ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനും അവയുടെ ഘടകങ്ങൾ കണക്കാക്കുന്നതിനുമുള്ള ജോലികൾ ഉൾക്കൊള്ളുന്നു- കോണുകൾ, പ്രദേശങ്ങൾ.

IN പാഠ്യപദ്ധതിപോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള ചുമതലകൾ നിയുക്തമാക്കിയിരിക്കുന്നു 2 അക്കാദമിക് സമയം, ഈ വിഷയം പഠിക്കാൻ പര്യാപ്തമല്ല. സ്കൂളിൽ, സ്റ്റീരിയോമെട്രിയുടെ സിദ്ധാന്തങ്ങളുടെയും സിദ്ധാന്തങ്ങളുടെയും അടിസ്ഥാനത്തിൽ മാത്രമാണ് പോളിഹെഡ്രയുടെ തലം ഭാഗങ്ങൾ നിർമ്മിക്കുന്നത്. അതേ സമയം, പോളിഹെഡ്രയുടെ പരന്ന ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള മറ്റ് രീതികളുണ്ട്. ട്രെയ്സ് രീതി, ആന്തരിക ഡിസൈൻ രീതി, സംയോജിത രീതി എന്നിവയാണ് ഏറ്റവും ഫലപ്രദമായത്. പരിഹാരത്തിനുള്ള അപേക്ഷയുടെ കാര്യത്തിൽ വളരെ രസകരവും വാഗ്ദാനവുമാണ് വിവിധ ജോലികൾകോർഡിനേറ്റ് രീതി. പോളിഹെഡ്രോൺ ഒരു കോർഡിനേറ്റ് സിസ്റ്റത്തിൽ സ്ഥാപിക്കുകയും കട്ടിംഗ് തലം ഒരു സമവാക്യം ഉപയോഗിച്ച് വ്യക്തമാക്കുകയും ചെയ്താൽ, വിഭാഗം നിർമ്മിക്കുന്നത് പോളിഹെഡ്രോണിൻ്റെ അരികുകളുള്ള വിമാനത്തിൻ്റെ വിഭജന പോയിൻ്റുകളുടെ കോർഡിനേറ്റുകൾ കണ്ടെത്തുന്നതിലേക്ക് ചുരുക്കും.

പഠന വിഷയം: പോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ.

പഠനത്തിൻ്റെ ഉദ്ദേശം: പഠനം വിവിധ രീതികൾപോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നു.

ഗവേഷണ ലക്ഷ്യങ്ങൾ:

1) ഈ വിഷയത്തെക്കുറിച്ചുള്ള സൈദ്ധാന്തിക മെറ്റീരിയൽ പഠിക്കുക.

2) വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ വ്യവസ്ഥാപിതമാക്കുക.

3) ഓരോ രീതിയും ഉപയോഗിക്കുന്നതിനുള്ള ജോലികളുടെ ഉദാഹരണങ്ങൾ നൽകുക.

4) വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിലും അവയുടെ ഘടകങ്ങൾ കണക്കാക്കുന്നതിലും ഏകീകൃത സംസ്ഥാന പരീക്ഷയിലെ പ്രശ്നങ്ങളുടെ ഉദാഹരണങ്ങൾ പരിഗണിക്കുക.

വിഭാഗം 1

പോളിഹെഡ്രോണുകളുടെ വിഭാഗങ്ങളുടെ നിർമ്മാണം

സീറോമെട്രിയുടെ ആക്‌സിയോം സിസ്റ്റത്തെ അടിസ്ഥാനമാക്കി

നിർവ്വചനം. ഒരു തലം വഴി ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം വിളിക്കുന്നു ജ്യാമിതീയ രൂപം, ബഹിരാകാശത്തെ എല്ലാ പോയിൻ്റുകളുടെയും ഗണമാണ്, അത് ഒരേസമയം നൽകിയിരിക്കുന്ന ഒരു പോളിഹെഡ്രോണിലും തലത്തിലും പെടുന്നു; വിമാനത്തെ കട്ടിംഗ് പ്ലെയിൻ എന്ന് വിളിക്കുന്നു.

ഒരു പോളിഹെഡ്രോണിൻ്റെ ഉപരിതലത്തിൽ അരികുകളും - ഭാഗങ്ങളും മുഖങ്ങളും - പരന്ന ബഹുഭുജങ്ങൾ അടങ്ങിയിരിക്കുന്നു. ഒരു നേർരേഖയും ഒരു തലവും ഒരു ബിന്ദുവിൽ വിഭജിക്കുകയും രണ്ട് തലങ്ങൾ ഒരു നേർരേഖയിലൂടെ വിഭജിക്കുകയും ചെയ്യുന്നതിനാൽ, ഒരു തലം കൊണ്ട് ഒരു പോളിഹെഡ്രോണിൻ്റെ ഭാഗം ഒരു തലം ബഹുഭുജമാണ്; ഈ ബഹുഭുജത്തിൻ്റെ ലംബങ്ങൾ പോളിഹെഡ്രോണിൻ്റെ അരികുകളുള്ള കട്ടിംഗ് തലത്തിൻ്റെ വിഭജന പോയിൻ്റുകളാണ്, കൂടാതെ വശങ്ങൾ കട്ടിംഗ് തലം അതിൻ്റെ മുഖങ്ങളെ വിഭജിക്കുന്ന ഭാഗങ്ങളാണ്. α എന്ന തലം ഉപയോഗിച്ച് തന്നിരിക്കുന്ന പോളിഹെഡ്രോണിൻ്റെ ആവശ്യമുള്ള ഭാഗം നിർമ്മിക്കുക എന്നാണ് ഇതിനർത്ഥം പോളിഹെഡ്രോണിൻ്റെ അരികുകൾ ഉപയോഗിച്ച് അതിൻ്റെ കവലയുടെ പോയിൻ്റുകൾ നിർമ്മിക്കാൻ ഇത് മതിയാകും. തുടർന്ന് ഈ പോയിൻ്റുകൾ തുടർച്ചയായി സെഗ്‌മെൻ്റുകളുമായി ബന്ധിപ്പിക്കുക.

കട്ടിംഗ് പ്ലെയിൻ α ഇപ്രകാരം വ്യക്തമാക്കാം: ഒരേ നേർരേഖയിൽ കിടക്കാത്ത മൂന്ന് പോയിൻ്റുകൾ; ഒരു നേർരേഖയും അതിൽ ഉൾപ്പെടാത്ത ഒരു ബിന്ദുവും; തന്നിരിക്കുന്ന പോളിഹെഡ്രോണുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ അതിൻ്റെ സ്ഥാനം നിർണ്ണയിക്കുന്ന മറ്റ് വ്യവസ്ഥകൾ. ഉദാഹരണത്തിന്, ചിത്രം 1-ൽ, ചതുരാകൃതിയിലുള്ള പിരമിഡിൻ്റെ PABCD യുടെ ഒരു ഭാഗം നിർമ്മിച്ചിരിക്കുന്നത്, യഥാക്രമം PC, PD, PB എന്നീ അരികുകളിൽ ഉൾപ്പെടുന്ന M, K, H എന്നീ പോയിൻ്റുകളാൽ നിർവചിക്കപ്പെട്ടിട്ടുള്ള പ്ലെയിൻ α ആണ്;

ചിത്രം.1

ടാസ്ക്. സമാന്തരമായി എബിസിയിൽ DA 1 B 1 C 1 D 1 വിമാനം വഴി ഒരു വിഭാഗം നിർമ്മിക്കുക, കൊടുമുടികളിലൂടെ കടന്നുപോകുന്നുസെഗ്മെൻ്റ് ബി 1 സി 1 (ചിത്രം 2, എ) യുടെ സി, ഡി 1, പോയിൻ്റ് കെ.

പരിഹാരം. 1. ടി. ലേക്ക് . കൂടെ ∈ DD 1 C 1, D 1 ∈ DD 1 C 1, തുടർന്ന് സിദ്ധാന്തമനുസരിച്ച് (രണ്ട് പോയിൻ്റുകളിലൂടെ, വിമാനത്തിൻ്റേത്, ഒരു നേർരേഖയിലൂടെ കടന്നുപോകുന്നു, ഒന്നു മാത്രം) ഡിഡി 1 സി 1 വിമാനത്തിൽ ഒരു ട്രെയ്സ് സിഡി 1 നിർമ്മിക്കാം (ചിത്രം 2, ബി).

2. അതുപോലെ വിമാനത്തിൽ എ 1 B 1 C 1 ഞങ്ങൾ ഒരു ട്രെയ്സ് DK നിർമ്മിക്കും, BB 1 C 1 വിമാനത്തിൽ ഞങ്ങൾ ഒരു ട്രെയ്സ് CK നിർമ്മിക്കും.

3. D 1 KC – ആവശ്യമുള്ള വിഭാഗം (ചിത്രം..2, സി)

എ ബി സി)

ചിത്രം.2

ടാസ്ക്. പിരമിഡ് RABC യുടെ ഒരു ഭാഗം പ്ലെയിൻ α = (MKH) ഉപയോഗിച്ച് നിർമ്മിക്കുക, ഇവിടെ M, K, H എന്നിവ യഥാക്രമം RS, PB, AB എന്നിവയുടെ അരികുകളുടെ ആന്തരിക പോയിൻ്റുകളാണ് (ചിത്രം 3, a).

പരിഹാരം. 1st ഘട്ടം. α, RVS എന്നീ രണ്ട് പ്ലെയിനുകളിൽ ഓരോന്നിലും M, K പോയിൻ്റുകൾ കിടക്കുന്നു. അതിനാൽ, രണ്ട് വിമാനങ്ങളുടെ വിഭജനത്തിൻ്റെ സിദ്ധാന്തമനുസരിച്ച്, α തലം MK എന്ന നേർരേഖയിലൂടെ RVS തലത്തെ വിഭജിക്കുന്നു. തത്ഫലമായി, സെഗ്മെൻ്റ് MK ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ വശങ്ങളിൽ ഒന്നാണ് (ചിത്രം 3, ബി).

രണ്ടാം ഘട്ടം. അതുപോലെ, സെഗ്മെൻ്റ് KN എന്നത് ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ മറുവശമാണ് (ചിത്രം 3, c).

3-ആം ഘട്ടം. RABC എന്ന പിരമിഡിൻ്റെ മുഖങ്ങളിലൊന്നും M, H പോയിൻ്റുകൾ ഒരേസമയം കിടക്കുന്നില്ല, അതിനാൽ MH സെഗ്‌മെൻ്റ് ഈ പിരമിഡിൻ്റെ വിഭാഗത്തിൻ്റെ ഒരു വശമല്ല. KN, RA എന്നീ നേർരേഖകൾ AVR മുഖത്തിൻ്റെ തലത്തിൽ കിടക്കുകയും വിഭജിക്കുകയും ചെയ്യുന്നു. നമുക്ക് T= KH ∩AP (ചിത്രം 3, d) എന്ന പോയിൻ്റ് നിർമ്മിക്കാം.

KN എന്ന നേർരേഖ α തലത്തിൽ കിടക്കുന്നതിനാൽ, T എന്ന പോയിൻ്റ് α തലത്തിലാണ്. ഇപ്പോൾ നമ്മൾ കാണുന്നത് വിമാനങ്ങൾ α ആണ് APC, APC എന്നിവയ്ക്ക് പൊതുവായ പോയിൻ്റുകൾ M, T എന്നിവയുണ്ട്. തൽഫലമായി, രണ്ട് പ്ലെയിനുകളുടെ വിഭജനത്തിൻ്റെ തത്വമനുസരിച്ച്, പ്ലെയിൻ α, പ്ലെയിൻ APC എന്നിവ നേർരേഖയായ MT യിലൂടെ വിഭജിക്കുന്നു, ഇത് R പോയിൻ്റിൽ എഡ്ജ് എസിയെ വിഭജിക്കുന്നു (ചിത്രം 3, e) .

നാലാം ഘട്ടം. ഇപ്പോൾ, ഘട്ടം 1-ലെ അതേ രീതിയിൽ, വിമാനം യഥാക്രമം MR, HR എന്നീ സെഗ്‌മെൻ്റുകൾക്കൊപ്പം ACP, ABC എന്നീ മുഖങ്ങളെ വിഭജിക്കുന്നുവെന്ന് ഞങ്ങൾ സ്ഥാപിക്കുന്നു. തത്ഫലമായി, ആവശ്യമായ വിഭാഗം ചതുർഭുജ MKHR ആണ് (ചിത്രം 3, f).

ചിത്രം.3

കൂടുതൽ സങ്കീർണ്ണമായ ഒരു പ്രശ്നം പരിഗണിക്കാം.

ടാസ്ക് . പെൻ്റഗണൽ പിരമിഡിൻ്റെ PABCDE യുടെ ഒരു ഭാഗം വിമാനം വഴി നിർമ്മിക്കുക

α = (KQR), ഇവിടെ K, Q എന്നത് യഥാക്രമം RA, RS എന്നീ അരികുകളുടെ ആന്തരിക പോയിൻ്റുകളാണ്, കൂടാതെ പോയിൻ്റ് R എന്നത് DPE യുടെ മുഖത്തിനകത്താണ് (ചിത്രം 4, a).

പരിഹാരം . QK, AC എന്നീ വരികൾ ഒരേ തലം ACP യിൽ കിടക്കുന്നു (ഒരു നേർരേഖയുടെയും ഒരു തലത്തിൻ്റെയും സിദ്ധാന്തമനുസരിച്ച്) ടി ചില പോയിൻ്റിൽ വിഭജിക്കുന്നു 1 , (ചിത്രം 4, ബി), അതേസമയം ടി 1 є α, മുതൽ QК є α.

നേർരേഖ PR, DE യെ ചില പോയിൻ്റിൽ F (ചിത്രം 4, c) വിഭജിക്കുന്നു, ഇത് പിരമിഡിൻ്റെ അടിത്തറയുടെ ARR, സൈഡ് DE എന്നിവയുടെ വിഭജന പോയിൻ്റാണ്. അപ്പോൾ KR, AF എന്നീ വരികൾ ഒരേ തലം ARR-ൽ കിടക്കുന്നു, ചില പോയിൻ്റുകളിൽ ടി വിഭജിക്കുന്നു 2 (ചിത്രം 4, ഡി), അതേസമയം ടി 2 є α , നേർരേഖയുടെ ഒരു ബിന്ദുവായി KR є α (നേർരേഖയുടെയും തലത്തിൻ്റെയും സിദ്ധാന്തം അനുസരിച്ച്).

സ്വീകരിച്ചത്: നേരെ ടി 1 ടി 2 സെക്കൻ്റ് തലം α യിലും പിരമിഡിൻ്റെ അടിത്തറയുടെ തലത്തിലും (നേർരേഖയുടെയും തലത്തിൻ്റെയും സിദ്ധാന്തമനുസരിച്ച്), നേർരേഖ യഥാക്രമം പിരമിഡിൻ്റെ അടിസ്ഥാന എബിസിഡിഇയുടെ DE, AE എന്നീ വശങ്ങളെ വിഭജിക്കുന്നു. M, N എന്നീ പോയിൻ്റുകളിൽ (ചിത്രം 4, e), പിരമിഡിൻ്റെ DE, AE എന്നീ അരികുകളുള്ള വിമാനം α ഛേദിക്കുന്ന പോയിൻ്റുകളും ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ ലംബങ്ങളായി വർത്തിക്കുന്നു.

കൂടാതെ, നേർരേഖ MR മുഖം DPE യുടെ തലത്തിലും കട്ടിംഗ് പ്ലെയിനിലും α (ഒരു നേർരേഖയുടെയും ഒരു തലത്തിൻ്റെയും സിദ്ധാന്തമനുസരിച്ച്), എഡ്ജ് PD-യെ ചില ഘട്ടത്തിൽ വിഭജിക്കുമ്പോൾ H - ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ മറ്റൊരു ശീർഷകം. (ചിത്രം 4, f).

അടുത്തതായി, നമുക്ക് പോയിൻ്റ് ടി നിർമ്മിക്കാം 3 - ടി 1 ടി 2 ∩ AB (ചിത്രം 4, g), ഇത്, T എന്ന നേർരേഖയുടെ ഒരു ബിന്ദുവായി 1 ടി 2 є α, ഒരു തലത്തിൽ കിടക്കുന്നു (രേഖയുടെയും തലത്തിൻ്റെയും സിദ്ധാന്തം അനുസരിച്ച്). ഇപ്പോൾ RAB മുഖത്തിൻ്റെ തലം രണ്ട് പോയിൻ്റ് T യുടെതാണ് 3 ഒപ്പം കട്ടിംഗ് പ്ലെയിനിലേക്ക് α, അതായത് നേർരേഖ ടി 3 ഈ വിമാനങ്ങളുടെ കവലയുടെ നേർരേഖയാണ് കെ. നേരെ ടി 3 ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ അടുത്ത ശീർഷകമായി വർത്തിക്കുന്ന പോയിൻ്റ് എൽ (ചിത്രം 4, h) ൽ കെ എഡ്ജ് പിബിയെ വിഭജിക്കുന്നു.

അതിനാൽ, ആവശ്യമുള്ള വിഭാഗം നിർമ്മിക്കുന്നതിനുള്ള ശ്രേണിയുടെ "ചെയിൻ" ഇപ്രകാരമാണ്:

1. ടി 1 = QK∩എ.സി ; 2. F = PR ∩ DE;

3. ടി 2 = KR ∩ AF; 4.എം = ടി 1 ടി 2 ∩ DE;

5.N=ടി 1 ടി 2 ∩ എ.ഇ ; 6. എൻ = MR ∩ PD;

7. ടി 3 = ടി 1 ടി 2 ∩ എബി ; 8.L=T 3 കെ ∩ പി.ബി.

ഷഡ്ഭുജ MNKLQH ആണ് ആവശ്യമായ വിഭാഗം.

ചിത്രം.4

സമാന്തര മുഖങ്ങളുള്ള (പ്രിസം, സമാന്തരപൈപ്പ്ഡ് ക്യൂബ്) ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം സമാന്തര തലങ്ങളുടെ സവിശേഷതകൾ ഉപയോഗിച്ച് നിർമ്മിക്കാം.

ടാസ്ക് . എം, പി, ആർ പോയിൻ്റുകൾ സമാന്തരപൈപ്പിൻ്റെ അരികുകളിൽ സ്ഥിതിചെയ്യുന്നു. സമാന്തര ലൈനുകളുടെയും പ്ലെയിനുകളുടെയും ഗുണവിശേഷതകൾ ഉപയോഗിച്ച്, MPR പ്ലെയിൻ ഉപയോഗിച്ച് ഈ സമാന്തര പൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക.

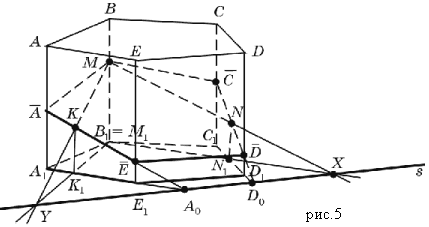
പരിഹാരം. DD യുടെ അരികുകളിൽ യഥാക്രമം M, P, R എന്നീ പോയിൻ്റുകൾ സ്ഥിതിചെയ്യട്ടെ 1, BB 1, SS 1 സമാന്തര പൈപ്പ് എബിസിബിഎ 1 ബി 1 സി 1 ബി 1 (ചിത്രം 5, എ).

നമുക്ക് സൂചിപ്പിക്കാം: (MPR) = α - കട്ടിംഗ് വിമാനം. ഞങ്ങൾ എംആർ, പിആർ (ചിത്രം 5, ബി) സെഗ്‌മെൻ്റുകൾ വരയ്ക്കുന്നു, അതിനൊപ്പം വിമാനം യഥാക്രമം സിസി മുഖങ്ങളെ വിഭജിക്കുന്നു. 1 D 1 D, BB 1 C 1 ഈ സമാന്തര പൈപ്പിൽ നിന്ന്. MR, PR എന്നീ സെഗ്‌മെൻ്റുകൾ ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ വശങ്ങളാണ്. അടുത്തതായി ഞങ്ങൾ മൂന്നാമത്തേത് ഉള്ള രണ്ട് സമാന്തര തലങ്ങളുടെ കവലയിൽ സിദ്ധാന്തങ്ങൾ ഉപയോഗിക്കുന്നു.

മുഖം AA 1 B 1 ആയതിനാൽ ബി സിസിയെ അഭിമുഖീകരിക്കുന്നതിന് സമാന്തരമാണ് 1 ഡി 1 ഡി, പിന്നെ മുഖത്തിൻ്റെ AA യുടെ തലം α വിമാനത്തിൻ്റെ കവലയുടെ നേർരേഖ 1 ൽ 1 B വരി MR-ന് സമാന്തരമായിരിക്കണം. അതിനാൽ നമ്മൾ സെഗ്മെൻ്റ് PQ || MR, Q є AB (ചിത്രം 5, c); സെഗ്മെൻ്റ് PQ എന്നത് ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ അടുത്ത വശമാണ്. അതുപോലെ, മുഖം AA മുതൽ 1 ഡി 1 ഡി സിസിയെ അഭിമുഖീകരിക്കുന്നതിന് സമാന്തരമാണ് 1 ൽ 1 B, പിന്നെ മുഖത്തിൻ്റെ AA യുടെ തലം α വിമാനത്തിൻ്റെ കവലയുടെ നേർരേഖ 1 ഡി 1 D വരി PR-ന് സമാന്തരമായിരിക്കണം. അതിനാൽ, ഞങ്ങൾ സെഗ്മെൻ്റ് MH || PR, H = AD (ചിത്രം 5, c); സെഗ്മെൻ്റ് MH എന്നത് ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ മറ്റൊരു വശമാണ്. മുഖം ABCD യുടെ AB, AD എന്നീ അരികുകളിൽ, പോയിൻ്റുകൾ Q є AB, H є AD എന്നിവ നിർമ്മിച്ചു, അവ ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ ലംബങ്ങളാണ്. ഞങ്ങൾ സെഗ്മെൻ്റ് ക്യുഎച്ച് വരച്ച് പെൻ്റഗൺ എംആർപിക്യുഎച്ച് - സമാന്തരപൈപ്പിൻ്റെ ആവശ്യമുള്ള വിഭാഗം നേടുക.

എ ബി സി)

അരി. 5

വിഭാഗം 2

പോളിഹെഡ്രോണുകളുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള ട്രെയ്സ് രീതി

നിർവ്വചനം. കട്ടിംഗ് തലം α പോളിഹെഡ്രോണിൻ്റെ അടിത്തറയുടെ തലത്തെ വിഭജിക്കുന്ന നേർരേഖയെ ഈ അടിത്തറയുടെ തലത്തിൽ α തലത്തിൻ്റെ ട്രെയ്സ് എന്ന് വിളിക്കുന്നു.

ഒരു ട്രെയ്‌സിൻ്റെ നിർവചനത്തിൽ നിന്ന് നമുക്ക് ലഭിക്കുന്നത്: അതിൻ്റെ ഓരോ പോയിൻ്റിലും നേർരേഖകൾ വിഭജിക്കുന്നു, അവയിലൊന്ന് സെക്കൻ്റ് തലത്തിലും മറ്റൊന്ന് അടിത്തറയുടെ തലത്തിലും. ട്രേസ് രീതി ഉപയോഗിച്ച് പോളിഹെഡ്രയുടെ പ്ലെയിൻ സെക്ഷനുകൾ നിർമ്മിക്കുമ്പോൾ ട്രെയ്സിൻ്റെ ഈ സ്വത്താണ് ഉപയോഗിക്കുന്നത്. ഈ സാഹചര്യത്തിൽ, കട്ടിംഗ് വിമാനത്തിൽ പോളിഹെഡ്രോണിൻ്റെ അറ്റങ്ങൾ വിഭജിക്കുന്ന നേർരേഖകൾ ഉപയോഗിക്കുന്നത് സൗകര്യപ്രദമാണ്.

ആദ്യം, പ്രിസത്തിൻ്റെ (പിരമിഡ്) അടിത്തറയുടെ (പിരമിഡ്) തലത്തിലും പ്രിസത്തിൻ്റെ (പിരമിഡ്) ഉപരിതലത്തിൽ പെടുന്ന ഒരു പോയിൻ്റിലും അതിൻ്റെ ട്രെയ്സ് ഉപയോഗിച്ച് ഞങ്ങൾ സെക്കൻ്റ് പ്ലെയിനിനെ നിർവചിക്കുന്നു.

ടാസ്ക്. ABCVEA പ്രിസത്തിൻ്റെ ഒരു ക്രോസ് സെക്ഷൻ നിർമ്മിക്കുക 1 ബി 1 സി 1 ഡി 1 ഇ 1 വിമാനം α, അത് താഴെ നൽകിയിരിക്കുന്നുഎൽ പ്രിസത്തിൻ്റെ അടിത്തറയുടെ എബിസി തലത്തിൽ, എഡ്ജ് ഡിഡിയിൽ ഉൾപ്പെടുന്ന പോയിൻ്റ് എം 1 (ചിത്രം 7, എ).

പരിഹാരം. വിശകലനം. പെൻ്റഗൺ MNPQR ആവശ്യമുള്ള വിഭാഗമാണെന്ന് നമുക്ക് അനുമാനിക്കാം (ചിത്രം 6). ഈ പരന്ന പെൻ്റഗൺ നിർമ്മിക്കുന്നതിന്, അതിൻ്റെ ശീർഷകങ്ങൾ N, P, Q, R (പോയിൻ്റ് M നൽകിയിരിക്കുന്നു) - യഥാക്രമം CC അരികുകളുള്ള കട്ടിംഗ് പ്ലെയിനിൻ്റെ വിഭജനത്തിൻ്റെ പോയിൻ്റുകൾ നിർമ്മിച്ചാൽ മതി.ഈ പ്രിസത്തിൻ്റെ 1, BB 1, AA 1, EE 1.

അരി. 6

പോയിൻ്റ് നിർമ്മിക്കുന്നതിന് N = α ∩ СС 1 കട്ടിംഗ് പ്ലെയിൻ α ൻ്റെ കവലയുടെ നേർരേഖ, മുഖം SDD യുടെ തലം ഉപയോഗിച്ച് നിർമ്മിക്കാൻ ഇത് മതിയാകും. 1 സി 1 . ഇത് ചെയ്യുന്നതിന്, ഈ മുഖത്തിൻ്റെ തലത്തിൽ മറ്റൊരു പോയിൻ്റ് നിർമ്മിക്കാൻ മതിയാകും, കട്ടിംഗ് പ്ലെയിൻ α യുടെ ഭാഗമാണ്. അത്തരമൊരു പോയിൻ്റ് എങ്ങനെ നിർമ്മിക്കാം?

നേരായതിനാൽ എൽ പ്രിസത്തിൻ്റെ അടിത്തറയുടെ തലത്തിലാണ് സ്ഥിതി ചെയ്യുന്നത്, അപ്പോൾ അതിന് സിഡിഡി മുഖത്തിൻ്റെ തലം വിഭജിക്കാൻ കഴിയും 1 സി 1 CD = (CDD) എന്ന വരിയിൽ പെടുന്ന പോയിൻ്റിൽ മാത്രം 1 ) ∩ (ABC), അതായത്. പോയിൻ്റ് X =എൽ∩CD = എൽ∩ (CDD 1 ) കട്ടിംഗ് വിമാനം α യുടെതാണ്. അങ്ങനെ, പോയിൻ്റ് N = α ∩ СС നിർമ്മിക്കാൻ 1 X = എന്ന പോയിൻ്റ് നിർമ്മിച്ചാൽ മതിഎൽ ∩CD. അതുപോലെ, പോയിൻ്റുകൾ നിർമ്മിക്കാൻ P = α ∩ BB 1, Q = α ∩ AA 1, R = α ∩ EE 1 അതനുസരിച്ച് പോയിൻ്റുകൾ നിർമ്മിച്ചാൽ മതി: Y =എൽ∩ BC, Z = എൽ∩ AB, T = എൽ∩ എഇ. ഇവിടെ നിന്ന്

നിർമ്മാണം.

X = എൽ∩ സിഡി (ചിത്രം 7, ബി);

N = MX ∩ СС 1 (ചിത്രം 7, ബി);

Y = എൽ∩ BC (ചിത്രം 7, c);

P = NY ∩ BB 1 (ചിത്രം 7, c);

Z= എൽ∩ AB (ചിത്രം 7, c);

Q= PZ ∩ AA 1 (ചിത്രം 7, d);

ടി= എൽ∩ AE (ചിത്രം 6);

R= QT ∩ EE 1 (ചിത്രം 6).

പെൻ്റഗൺ MNPQR ആണ് ആവശ്യമായ വിഭാഗം (ചിത്രം 6).

തെളിവ് . നേരായതിനാൽ എൽ കട്ടിംഗ് പ്ലെയിനിൻ്റെ ട്രെയ്സ് ആണ് α, തുടർന്ന് പോയിൻ്റുകൾ X =എൽ∩ СD, Y = എൽ∩ BC, Z = എൽ∩ AB, T= എൽ ∩ AE ഈ വിമാനത്തിൻ്റേതാണ്.

അതിനാൽ ഞങ്ങൾക്ക് ഉണ്ട്:

М є α , X є α => МХ є α, പിന്നെ МХ ∩ СС 1 = N є α, അതായത് N = α ∩ СС 1 ;

N є α, Y є α => NY കൂടാതെ α, തുടർന്ന് NY ∩ ВВ 1 = Р є α, അതായത് Р = α ∩ ВВ 1 ;

Р є α, Z є α => РZ є α, പിന്നെ PZ ∩ AA 1 = Q є α, അതായത് Q = α ∩ AA 1 ;

Q є α, T є α => QТ є α, തുടർന്ന് QТ ∩ EE 1 =R є α, അതായത് R = α ∩ Е 1 .

അതിനാൽ, MNPQR ആവശ്യമായ വിഭാഗമാണ്.

a) b)

സി) ഡി)

അരി. 7

പഠനം. ട്രാക്ക് എൽ കട്ടിംഗ് പ്ലെയിൻ α പ്രിസത്തിൻ്റെ അടിത്തറയെ വിഭജിക്കുന്നില്ല, കൂടാതെ കട്ടിംഗ് പ്ലെയിനിൻ്റെ പോയിൻ്റ് M വശത്തിൻ്റെ അരികിലുള്ള DD യുടേതാണ്. 1 പ്രിസങ്ങൾ. അതിനാൽ, കട്ടിംഗ് വിമാനം α വശത്തെ അരികുകൾക്ക് സമാന്തരമല്ല. തൽഫലമായി, പ്രിസത്തിൻ്റെ ലാറ്ററൽ അറ്റങ്ങൾ (അല്ലെങ്കിൽ ഈ അരികുകളുടെ വിപുലീകരണങ്ങൾ) ഉള്ള ഈ തലത്തിൻ്റെ വിഭജനത്തിൻ്റെ N, P, Q, R എന്നീ പോയിൻ്റുകൾ എല്ലായ്പ്പോഴും നിലവിലുണ്ട്. കൂടാതെ, പോയിൻ്റ് എം ട്രെയ്‌സിൽ ഉൾപ്പെടാത്തതിനാൽഎൽ , അപ്പോൾ അവർ നിർവ്വചിച്ച വിമാനം α അതുല്യമാണ്. ഇതിനർത്ഥം പ്രശ്നത്തിന് ഒരു അദ്വിതീയ പരിഹാരമുണ്ടെന്നാണ്.

ടാസ്ക്. ഇനിപ്പറയുന്നവ നൽകിയിട്ടുള്ള വിമാനം ഉപയോഗിച്ച് പെൻ്റഗണൽ പിരമിഡ് PABCDE യുടെ ഒരു ഭാഗം നിർമ്മിക്കുകഎൽ ഒപ്പം എഡ്ജ് PE യുടെ ആന്തരിക പോയിൻ്റ് കെ.

പരിഹാരം. ആസൂത്രിതമായി, ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ നിർമ്മാണം ഇനിപ്പറയുന്ന രീതിയിൽ ചിത്രീകരിക്കാം (ചിത്രം 8): ടി 1 → Q → T 2 → R → T 3 → M → T 4 → N.

പെൻ്റഗൺ MNKQR ആണ് ആവശ്യമായ വിഭാഗം.

വിഭാഗത്തിൻ്റെ ലംബങ്ങൾ നിർമ്മിക്കുന്ന ക്രമത്തിൻ്റെ "ചെയിൻ" ഇപ്രകാരമാണ്:

1. ടി 1 = എൽ∩ AE; 2. Q = T 1 K ∩ RA;

3. T 2 = എൽ∩ എബി; 4. R = T 2 Q ∩ РВ;

5. T 3 = എൽ∩ BC; 6. M = T 3 R ∩ RS;

7. T 4 = എൽ∩CD; 8. N = T 4 M ∩ РD.

അരി. 8

കട്ടിംഗ് വിമാനം പലപ്പോഴും പോളിഹെഡ്രോണിൻ്റെ മൂന്ന് പോയിൻ്റുകളാൽ നിർവചിക്കപ്പെടുന്നു. ഈ സാഹചര്യത്തിൽ, ട്രെയ്സ് രീതി ഉപയോഗിച്ച് ആവശ്യമുള്ള വിഭാഗം നിർമ്മിക്കുന്നതിന്, ആദ്യം നൽകിയിരിക്കുന്ന പോളിഹെഡ്രോണിൻ്റെ അടിത്തറയുടെ തലത്തിൽ കട്ടിംഗ് പ്ലെയിനിൻ്റെ ഒരു ട്രെയ്സ് നിർമ്മിക്കുക.

വിഭാഗം 3

ഇൻ്റീരിയർ ഡിസൈൻ രീതി

പോളിഹെഡ്രോണുകളുടെ വിഭാഗങ്ങളുടെ നിർമ്മാണത്തിൽ

ആന്തരിക ഡിസൈൻ രീതിയെ കറസ്പോണ്ടൻസ് രീതി അല്ലെങ്കിൽ ഡയഗണൽ വിഭാഗങ്ങളുടെ രീതി എന്നും വിളിക്കുന്നു.

ഈ രീതി പ്രയോഗിക്കുമ്പോൾ, നൽകിയിരിക്കുന്ന ഓരോ പോയിൻ്റും അടിസ്ഥാന തലത്തിലേക്ക് പ്രൊജക്റ്റ് ചെയ്യുന്നു. രണ്ടെണ്ണം ഉണ്ട് സാധ്യമായ തരങ്ങൾഡിസൈൻ: കേന്ദ്രവും സമാന്തരവും. പിരമിഡുകളുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുമ്പോൾ സാധാരണയായി സെൻട്രൽ പ്രൊജക്ഷൻ ഉപയോഗിക്കുന്നു, പിരമിഡിൻ്റെ മുകൾഭാഗം പ്രൊജക്ഷൻ്റെ കേന്ദ്രമാണ്. പ്രിസത്തിൻ്റെ വിഭാഗങ്ങൾ നിർമ്മിക്കുമ്പോൾ സമാന്തര ഡിസൈൻ ഉപയോഗിക്കുന്നു.

ടാസ്ക് . M, F, R എന്നീ പോയിൻ്റുകൾ യഥാക്രമം RA, RS, PE എന്നിവയുടെ അരികുകളുടെ ആന്തരിക പോയിൻ്റുകളാണെങ്കിൽ, α = (MFR) പിരമിഡ് PABCDE യുടെ ഒരു വിഭാഗം നിർമ്മിക്കുക (ചിത്രം 9, a).

പരിഹാരം . പിരമിഡിൻ്റെ അടിത്തറയുടെ തലം β ആയി സൂചിപ്പിക്കാം. ആവശ്യമുള്ള വിഭാഗം നിർമ്മിക്കുന്നതിന്, പിരമിഡിൻ്റെ അരികുകളുള്ള കട്ടിംഗ് പ്ലെയിൻ α ൻ്റെ വിഭജനത്തിൻ്റെ പോയിൻ്റുകൾ ഞങ്ങൾ നിർമ്മിക്കുന്നു.

ഈ പിരമിഡിൻ്റെ എഡ്ജ് പിഡി ഉപയോഗിച്ച് കട്ടിംഗ് പ്ലെയിനിൻ്റെ ഇൻ്റർസെക്ഷൻ പോയിൻ്റ് നമുക്ക് നിർമ്മിക്കാം.

APD, CPE പ്ലെയിനുകൾ യഥാക്രമം AD, CE എന്നീ നേർരേഖകളിലൂടെ പ്ലെയിൻ β-നെ വിഭജിക്കുന്നു, ഇത് K (ചിത്രം 9, c). നേർരേഖ PK=(APD) ∩(CPE) FR є α എന്ന നേർരേഖയെ ചില ഘട്ടത്തിൽ K 1 മുതൽ 1 വരെ = RK ∩ FR (ചിത്രം 9, d), അതേസമയം കെ 1 є α. പിന്നെ: M є α, കെ 1 є α => നേർരേഖ MK є a. അതിനാൽ പോയിൻ്റ് Q = MK 1 ∩ PD (ചിത്രം 9, e) എഡ്ജ് PD യുടെയും കട്ടിംഗ് പ്ലെയിനിൻ്റെയും ഇൻ്റർസെക്ഷൻ പോയിൻ്റാണ്: Q = α ∩ PD. പോയിൻ്റ് Q എന്നത് ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ ശീർഷകമാണ്. അതുപോലെ, ഞങ്ങൾ തലം α, എഡ്ജ് പിബി എന്നിവയുടെ ഇൻ്റർസെക്ഷൻ പോയിൻ്റ് നിർമ്മിക്കുന്നു. BPE, АD പ്ലെയിനുകൾ യഥാക്രമം BE, AD എന്നീ നേർരേഖകളിലൂടെയുള്ള തലം β-യെ ഖണ്ഡിക്കുന്നു, അവ പോയിൻ്റ് H-ൽ വിഭജിക്കുന്നു (ചിത്രം 9, e). PH = (BPE) ∩ (APD) നേർരേഖ MQ നെ പോയിൻ്റ് H-ൽ വിഭജിക്കുന്നു 1 (ചിത്രം 9, g). അപ്പോൾ നേർരേഖ RN 1 പോയിൻ്റ് N = α ∩ PB - വിഭാഗത്തിൻ്റെ ശീർഷകം (ചിത്രം 9, h) എന്ന പോയിൻ്റിൽ എഡ്ജ് പിബിയെ വിഭജിക്കുന്നു.

1. K = AD ∩ EC; 2. K 1 = RK ∩ RF;

3.Q=എം.കെ 1 ∩ ആർ ഡി; 4. H = BE ∩എ ഡി;

5. Н 1 = РН ∩ МQ; 6. N = RН 1 ∩ РВ.

പെൻ്റഗൺ MNFQR ആണ് ആവശ്യമായ വിഭാഗം (ചിത്രം 9, i).

എ ബി സി)

എവിടെ)

g) h) i)

അരി. 9

ടാസ്ക് . ABCDEA പ്രിസത്തിൻ്റെ ഒരു ക്രോസ് സെക്ഷൻ നിർമ്മിക്കുക 1 ബി 1 സി 1 ഡി 1 ഇ 1 , തലം α, പോയിൻ്റ് M є BB നിർവചിച്ചിരിക്കുന്നത് 1, P DD 1, Q EE 1 (ചിത്രം 10).

പരിഹാരം. നമുക്ക് സൂചിപ്പിക്കാം: β - പ്രിസത്തിൻ്റെ താഴത്തെ അടിത്തറയുടെ തലം. ആവശ്യമുള്ള വിഭാഗം നിർമ്മിക്കുന്നതിന്, ഞങ്ങൾ പ്രിസത്തിൻ്റെ അറ്റങ്ങൾ ഉപയോഗിച്ച് വിമാനം α = (MPQ) കവല പോയിൻ്റുകൾ നിർമ്മിക്കുന്നു.

AA എന്ന എഡ്ജ് ഉപയോഗിച്ച് α വിമാനത്തിൻ്റെ വിഭജന പോയിൻ്റ് നമുക്ക് നിർമ്മിക്കാം 1 .

A 1 AD, BEE 1 എന്നീ വിമാനങ്ങൾ യഥാക്രമം AD, BE എന്നീ നേർരേഖകളിലൂടെ β തലത്തെ വിഭജിക്കുക, അത് യഥാക്രമം കെ. 1 AD, BEE 1 AA സമാന്തര അറ്റങ്ങളിലൂടെ കടന്നുപോകുക 1, BB 1 പ്രിസങ്ങൾക്ക് ഒരു പൊതു പോയിൻ്റ് K ഉണ്ട്, പിന്നെ നേർരേഖ KK 1 അവയുടെ വിഭജനം പോയിൻ്റ് K ലൂടെ കടന്നുപോകുന്നു, ഒപ്പം ബിബിയുടെ അരികിൽ സമാന്തരവുമാണ് 1 . ഈ വരിയുടെ വിഭജന പോയിൻ്റ് QM: K എന്ന വരി ഉപയോഗിച്ച് നമുക്ക് സൂചിപ്പിക്കാം 1 = KK 1 ∩ QM, KK 1 ║ BB 1 . ക്യുഎം є α മുതൽ, പിന്നെ കെ 1 α.

അരി. 10

സ്വീകരിച്ചത്: Р є α, കെ 1 є α => നേരെ RK 1 є α, അതേസമയം RK 1 ∩ AA 1 = R. പോയിൻ്റ് R വിമാനം α, എഡ്ജ് എഎ എന്നിവയുടെ കവല പോയിൻ്റായി വർത്തിക്കുന്നു 1 (R = α ∩ AA 1 ), അതിനാൽ ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ ശീർഷകം. അതുപോലെ, ഞങ്ങൾ പോയിൻ്റ് N = α ∩ СС നിർമ്മിക്കുന്നു 1 .

അതിനാൽ, ആവശ്യമുള്ള വിഭാഗം നിർമ്മിക്കുന്നതിനുള്ള "ഘട്ടങ്ങളുടെ" ക്രമം ഇപ്രകാരമാണ്:

K = AD ∩ BE; 2. K 1 = KK 1 ∩ MQ, KK 1 || ബിബി 1;

R = RK 1 ∩ AA 1 ; 4. H = EC ∩AD;

H 1 – HH 1 ∩ РR, НН 1 || CC 1; 6.N = QН 1 ∩ СС 1.

പെൻ്റഗൺ MNPQR ആണ് ആവശ്യമായ വിഭാഗം.

ഈ പാഠത്തിൽ നമ്മൾ ടെട്രാഹെഡ്രോണും അതിൻ്റെ ഘടകങ്ങളും (ടെട്രാഹെഡ്രോൺ എഡ്ജ്, ഉപരിതലം, മുഖങ്ങൾ, ലംബങ്ങൾ) നോക്കും. ടെട്രാഹെഡ്രോണിൽ സെക്ഷനുകൾ നിർമ്മിക്കുന്നതിനുള്ള നിരവധി പ്രശ്നങ്ങൾ ഞങ്ങൾ പരിഹരിക്കും പൊതു രീതിവിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിന്.

വിഷയം: ലൈനുകളുടെയും വിമാനങ്ങളുടെയും സമാന്തരത

പാഠം: ടെട്രാഹെഡ്രോൺ. ഒരു ടെട്രാഹെഡ്രോണിൽ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിൽ പ്രശ്നങ്ങൾ

ഒരു ടെട്രാഹെഡ്രോൺ എങ്ങനെ നിർമ്മിക്കാം? നമുക്ക് ഒരു ഏകപക്ഷീയ ത്രികോണം എടുക്കാം എബിസി. ഏതെങ്കിലും പോയിൻ്റ് ഡി, ഈ ത്രികോണത്തിൻ്റെ തലത്തിൽ കിടക്കുന്നില്ല. നമുക്ക് 4 ത്രികോണങ്ങൾ ലഭിക്കും. ഈ 4 ത്രികോണങ്ങളാൽ രൂപംകൊണ്ട ഉപരിതലത്തെ ടെട്രാഹെഡ്രോൺ എന്ന് വിളിക്കുന്നു (ചിത്രം 1.). ഈ പ്രതലത്താൽ ബന്ധിതമായ ആന്തരിക പോയിൻ്റുകളും ടെട്രാഹെഡ്രോണിൻ്റെ ഭാഗമാണ്.

അരി. 1. ടെട്രാഹെഡ്രോൺ എബിസിഡി

ടെട്രാഹെഡ്രോണിൻ്റെ ഘടകങ്ങൾ
എ,ബി, സി, ഡി - ടെട്രാഹെഡ്രോണിൻ്റെ ശിഖരങ്ങൾ.
എബി, എ.സി., എ.ഡി, ബി.സി., BD, സി.ഡി - ടെട്രാഹെഡ്രോൺ അറ്റങ്ങൾ.
എബിസി, എബിഡി, BDC, എ.ഡി.സി - ടെട്രാഹെഡ്രോൺ മുഖങ്ങൾ.

അഭിപ്രായം:ഫ്ലാറ്റ് എടുക്കാം എബിസിപിന്നിൽ ടെട്രാഹെഡ്രോൺ അടിസ്ഥാനം, എന്നിട്ട് പോയിൻ്റ് ഡിആണ് ടെട്രാഹെഡ്രോണിൻ്റെ ശീർഷകം. ടെട്രാഹെഡ്രോണിൻ്റെ ഓരോ അരികും രണ്ട് വിമാനങ്ങളുടെ വിഭജനമാണ്. ഉദാഹരണത്തിന്, വാരിയെല്ല് എബി- ഇത് വിമാനങ്ങളുടെ കവലയാണ് എബിഡിഒപ്പം എബിസി. ടെട്രാഹെഡ്രോണിൻ്റെ ഓരോ ശീർഷകവും മൂന്ന് തലങ്ങളുടെ വിഭജനമാണ്. വെർട്ടക്സ് എവിമാനങ്ങളിൽ കിടക്കുന്നു എബിസി, എബിഡി, എഡികൂടെ. ഡോട്ട് എമൂന്ന് നിയുക്ത വിമാനങ്ങളുടെ കവലയാണ്. ഈ വസ്തുത ഇനിപ്പറയുന്ന രീതിയിൽ എഴുതിയിരിക്കുന്നു: എ= എബിസി ∩ എബിഡി ∩ എ.സിഡി.

ടെട്രാഹെഡ്രോൺ നിർവ്വചനം

അതിനാൽ, ടെട്രാഹെഡ്രോൺനാല് ത്രികോണങ്ങളാൽ രൂപപ്പെട്ട ഒരു ഉപരിതലമാണ്.

ടെട്രാഹെഡ്രോൺ എഡ്ജ്- ടെട്രാഹെഡ്രോണിൻ്റെ രണ്ട് വിമാനങ്ങളുടെ കവലയുടെ രേഖ.

6 പൊരുത്തങ്ങളിൽ നിന്ന് 4 തുല്യ ത്രികോണങ്ങൾ ഉണ്ടാക്കുക. ഒരു വിമാനത്തിൽ പ്രശ്നം പരിഹരിക്കുക അസാധ്യമാണ്. കൂടാതെ ബഹിരാകാശത്ത് ഇത് ചെയ്യാൻ എളുപ്പമാണ്. നമുക്ക് ഒരു ടെട്രാഹെഡ്രോൺ എടുക്കാം. 6 പൊരുത്തങ്ങൾ അതിൻ്റെ അരികുകളാണ്, ടെട്രാഹെഡ്രോണിൻ്റെ നാല് മുഖങ്ങളും നാല് തുല്യ ത്രികോണങ്ങളുമായിരിക്കും. പ്രശ്നം പരിഹരിച്ചു.

ഒരു ടെട്രാഹെഡ്രോൺ നൽകിയിരിക്കുന്നു എബിസിഡി. ഡോട്ട് എംടെട്രാഹെഡ്രോണിൻ്റെ ഒരു അരികിൽ പെടുന്നു എബി, ഡോട്ട് എൻടെട്രാഹെഡ്രോണിൻ്റെ ഒരു അരികിൽ പെടുന്നു INഡികാലഘട്ടവും ആർഅരികിൽ പെടുന്നു ഡികൂടെ(ചിത്രം 2.). ഒരു വിമാനം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക എം.എൻ.പി.

അരി. 2. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 2 - ഒരു ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം ഒരു വിമാനം ഉപയോഗിച്ച് നിർമ്മിക്കുക

പരിഹാരം:
ടെട്രാഹെഡ്രോണിൻ്റെ മുഖം പരിഗണിക്കുക ഡിസൂര്യൻ. പോയിൻ്റിൻ്റെ ഈ മുഖത്ത് എൻഒപ്പം പിമുഖങ്ങളുടേതാണ് ഡിസൂര്യൻ, അതിനാൽ ടെട്രാഹെഡ്രോൺ. എന്നാൽ പോയിൻ്റിൻ്റെ അവസ്ഥ അനുസരിച്ച് എൻ, പികട്ടിംഗ് വിമാനത്തിൻ്റേതാണ്. അർത്ഥമാക്കുന്നത്, എൻ.പി- ഇത് രണ്ട് വിമാനങ്ങളുടെ കവലയുടെ രേഖയാണ്: മുഖത്തിൻ്റെ തലം ഡിസൂര്യൻകട്ടിംഗ് വിമാനവും. നേർരേഖകൾ എന്ന് നമുക്ക് അനുമാനിക്കാം എൻ.പിഒപ്പം സൂര്യൻസമാന്തരമല്ല. അവർ ഒരേ വിമാനത്തിൽ കിടക്കുന്നു ഡിസൂര്യൻ.വരികളുടെ വിഭജന പോയിൻ്റ് നമുക്ക് കണ്ടെത്താം എൻ.പിഒപ്പം സൂര്യൻ. നമുക്ക് അത് സൂചിപ്പിക്കാം ഇ(ചിത്രം 3.).

അരി. 3. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 2. പോയിൻ്റ് കണ്ടെത്തൽ E

ഡോട്ട് ഇവിഭാഗം വിമാനത്തിൻ്റേതാണ് എം.എൻ.പി, അത് ലൈനിൽ കിടക്കുന്നതിനാൽ എൻ.പി, നേർരേഖയും എൻ.പിസെക്ഷൻ പ്ലെയിനിൽ പൂർണ്ണമായും കിടക്കുന്നു എം.എൻ.പി.

കൂടാതെ പോയിൻ്റ് ഇഒരു വിമാനത്തിൽ കിടക്കുന്നു എബിസി, കാരണം അത് ഒരു നേർരേഖയിലാണ് കിടക്കുന്നത് സൂര്യൻവിമാനത്തിന് പുറത്ത് എബിസി.

ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു കഴിക്കുക- വിമാനങ്ങളുടെ കവലയുടെ വരി എബിസിഒപ്പം എം.എൻ.പി.പോയിൻ്റുകൾ മുതൽ ഇഒപ്പം എംരണ്ട് വിമാനങ്ങളിൽ ഒരേസമയം കിടക്കുക - എബിസിഒപ്പം എം.എൻ.പി.നമുക്ക് ഡോട്ടുകൾ ബന്ധിപ്പിക്കാം എംഒപ്പം ഇ, നേരെ തുടരുക കഴിക്കുകവരിയുള്ള കവലയിലേക്ക് എ.സി. വരികളുടെ വിഭജന പോയിൻ്റ് കഴിക്കുകഒപ്പം എ.സിനമുക്ക് സൂചിപ്പിക്കാം ക്യു.

അതിനാൽ ഈ കേസിൽ NPQM- ആവശ്യമായ വിഭാഗം.

അരി. 4. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 2. പ്രശ്നത്തിൻ്റെ പരിഹാരം 2

എപ്പോഴാണെന്ന് നമുക്ക് ഇപ്പോൾ പരിഗണിക്കാം എൻ.പിസമാന്തരമായി ബി.സി.. നേരെയാണെങ്കിൽ എൻ.പിചില വരികൾക്ക് സമാന്തരമായി, ഉദാഹരണത്തിന്, ഒരു നേർരേഖ സൂര്യൻവിമാനത്തിന് പുറത്ത് എബിസി, പിന്നെ നേരെ എൻ.പിമുഴുവൻ വിമാനത്തിനും സമാന്തരമായി എബിസി.

ആവശ്യമുള്ള വിഭാഗം തലം നേർരേഖയിലൂടെ കടന്നുപോകുന്നു എൻ.പി, വിമാനത്തിന് സമാന്തരമായി എബിസി, ഒപ്പം ഒരു നേർരേഖയിൽ വിമാനത്തെ വിഭജിക്കുന്നു എം.ക്യു. അങ്ങനെ കവലയുടെ ലൈൻ എം.ക്യുവരയ്ക്ക് സമാന്തരമായി എൻ.പി. നമുക്ക് ലഭിക്കുന്നു NPQM- ആവശ്യമായ വിഭാഗം.

ഡോട്ട് എംവശത്ത് കിടക്കുന്നു എഡിINടെട്രാഹെഡ്രോൺ എബിസിഡി. പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക എംഅടിത്തറയ്ക്ക് സമാന്തരമായി എബിസി.

അരി. 5. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 3 ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം ഒരു വിമാനം ഉപയോഗിച്ച് നിർമ്മിക്കുക

പരിഹാരം:
കട്ടിംഗ് വിമാനം φ വിമാനത്തിന് സമാന്തരമായി എബിസിവ്യവസ്ഥ അനുസരിച്ച്, ഇതിനർത്ഥം ഈ വിമാനം എന്നാണ് φ വരികൾക്ക് സമാന്തരമായി എബി, എ.സി, സൂര്യൻ.
വിമാനത്തിൽ എബിഡിപോയിൻ്റിലൂടെ എംനമുക്ക് നേരിട്ട് നോക്കാം പി.ക്യുസമാന്തരമായി എബി(ചിത്രം 5). ഋജുവായത് പി.ക്യുഒരു വിമാനത്തിൽ കിടക്കുന്നു എബിഡി. അതുപോലെ വിമാനത്തിലും എ.സിഡിപോയിൻ്റിലൂടെ ആർനമുക്ക് നേരിട്ട് നോക്കാം പി.ആർസമാന്തരമായി എ.സി. ഒരു പോയിൻ്റ് കിട്ടി ആർ. വിഭജിക്കുന്ന രണ്ട് വരികൾ പി.ക്യുഒപ്പം പി.ആർവിമാനം PQRയഥാക്രമം രണ്ട് വിഭജിക്കുന്ന വരികൾക്ക് സമാന്തരമായി എബിഒപ്പം എ.സിവിമാനം എബിസി, അതായത് വിമാനങ്ങൾ എബിസിഒപ്പം PQRസമാന്തരമായി. PQR- ആവശ്യമായ വിഭാഗം. പ്രശ്നം പരിഹരിച്ചു.

ഒരു ടെട്രാഹെഡ്രോൺ നൽകിയിരിക്കുന്നു എബിസിഡി. ഡോട്ട് എം- ആന്തരിക പോയിൻ്റ്, ടെട്രാഹെഡ്രോണിൻ്റെ മുഖത്ത് പോയിൻ്റ് എബിഡി. എൻ- സെഗ്മെൻ്റിൻ്റെ ആന്തരിക പോയിൻ്റ് ഡികൂടെ(ചിത്രം 6.). ഒരു വരിയുടെ ഇൻ്റർസെക്ഷൻ പോയിൻ്റ് നിർമ്മിക്കുക എൻ.എം.വിമാനങ്ങളും എബിസി.

അരി. 6. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 4

പരിഹാരം:
ഇത് പരിഹരിക്കാൻ, ഞങ്ങൾ ഒരു സഹായ വിമാനം നിർമ്മിക്കും ഡിഎം.എൻ. അത് നേരെയാകട്ടെ ഡിഎംപോയിൻ്റിൽ AB രേഖയെ വിഭജിക്കുന്നു TO(ചിത്രം 7.). പിന്നെ, എസ്.കെഡി- ഇത് വിമാനത്തിൻ്റെ ഒരു ഭാഗമാണ് ഡിഎം.എൻടെട്രാഹെഡ്രോണും. വിമാനത്തിൽ ഡിഎം.എൻകള്ളവും നേരും എൻ.എം., ഫലമായുണ്ടാകുന്ന നേർരേഖയും എസ്.കെ. അങ്ങനെയാണെങ്കില് എൻ.എം.സമാന്തരമല്ല എസ്.കെ, പിന്നീട് അവ ഒരു ഘട്ടത്തിൽ കൂടിച്ചേരും ആർ. ഡോട്ട് ആർഒപ്പം വരിയുടെ ആവശ്യമുള്ള ഇൻ്റർസെക്ഷൻ പോയിൻ്റും ഉണ്ടാകും എൻ.എം.വിമാനങ്ങളും എബിസി.

അരി. 7. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 4. പ്രശ്നത്തിൻ്റെ പരിഹാരം 4

ഒരു ടെട്രാഹെഡ്രോൺ നൽകിയിരിക്കുന്നു എബിസിഡി. എം- മുഖത്തിൻ്റെ ആന്തരിക പോയിൻ്റ് എബിഡി. ആർ- മുഖത്തിൻ്റെ ആന്തരിക പോയിൻ്റ് എബിസി. എൻ- അരികിലെ ആന്തരിക പോയിൻ്റ് ഡികൂടെ(ചിത്രം 8.). പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക എം, എൻഒപ്പം ആർ.

അരി. 8. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 5 ഒരു ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം ഒരു വിമാനം ഉപയോഗിച്ച് നിർമ്മിക്കുക

പരിഹാരം:
നേർരേഖ വരുമ്പോൾ നമുക്ക് ആദ്യത്തെ കേസ് പരിഗണിക്കാം എം.എൻവിമാനത്തിന് സമാന്തരമല്ല എബിസി. മുമ്പത്തെ പ്രശ്നത്തിൽ ഞങ്ങൾ വരിയുടെ വിഭജന പോയിൻ്റ് കണ്ടെത്തി എം.എൻവിമാനങ്ങളും എബിസി. ഇതാണ് കാര്യം TO, ഇത് സഹായ തലം ഉപയോഗിച്ചാണ് ലഭിക്കുന്നത് ഡിഎം.എൻ, അതായത്. ഞങ്ങൾ ചെയ്യുന്നു ഡിഎംനമുക്ക് ഒരു പോയിൻ്റ് ലഭിക്കും എഫ്. ഞങ്ങൾ നടപ്പിലാക്കുന്നു CFകവലയിലും എം.എൻഞങ്ങൾക്ക് ഒരു പോയിൻ്റ് ലഭിക്കും TO.

അരി. 9. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 5. ഫൈൻഡിംഗ് പോയിൻ്റ് കെ

നമുക്ക് നേരിട്ട് ഉണ്ടാക്കാം KR. ഋജുവായത് KRസെക്ഷൻ തലത്തിലും വിമാനത്തിലും കിടക്കുന്നു എബിസി. പോയിൻ്റുകൾ നേടുന്നു പി 1ഒപ്പം R 2. ബന്ധിപ്പിക്കുന്നു പി 1ഒപ്പം എംഒരു തുടർച്ചയായി നമുക്ക് പോയിൻ്റ് ലഭിക്കും എം 1. ഡോട്ട് ബന്ധിപ്പിക്കുന്നു R 2ഒപ്പം എൻ. തൽഫലമായി, ഞങ്ങൾക്ക് ആവശ്യമുള്ള വിഭാഗം ലഭിക്കും Р 1 Р 2 NM 1. ആദ്യ കേസിലെ പ്രശ്നം പരിഹരിച്ചു.
നമുക്ക് രണ്ടാമത്തെ കേസ് പരിഗണിക്കാം, നേർരേഖ വരുമ്പോൾ എം.എൻവിമാനത്തിന് സമാന്തരമായി എബിസി. വിമാനം എം.എൻ.പിഒരു നേർരേഖയിലൂടെ കടന്നുപോകുന്നു എം.എൻവിമാനത്തിന് സമാന്തരമായി എബിസിവിമാനത്തെ ഖണ്ഡിക്കുകയും ചെയ്യുന്നു എബിസിചില നേർരേഖയിൽ R 1 R 2, പിന്നെ നേരെ R 1 R 2നൽകിയിരിക്കുന്ന വരിക്ക് സമാന്തരമായി എം.എൻ(ചിത്രം 10.).

അരി. 10. പ്രശ്നത്തിനുള്ള ഡ്രോയിംഗ് 5. ആവശ്യമായ വിഭാഗം

ഇനി നമുക്ക് ഒരു നേർരേഖ വരയ്ക്കാം ആർ 1 എംനമുക്ക് ഒരു പോയിൻ്റ് ലഭിക്കും എം 1.Р 1 Р 2 NM 1- ആവശ്യമായ വിഭാഗം.

അതിനാൽ, ഞങ്ങൾ ടെട്രാഹെഡ്രോണിലേക്ക് നോക്കി, ചിലത് പരിഹരിച്ചു സാധാരണ ജോലികൾഒരു ടെട്രാഹെഡ്രോണിലേക്ക്. അടുത്ത പാഠത്തിൽ നമ്മൾ ഒരു സമാന്തര പൈപ്പ് നോക്കും.

1. I. M. സ്മിർനോവ, V. A. സ്മിർനോവ്. - അഞ്ചാം പതിപ്പ്, തിരുത്തിയതും വിപുലീകരിച്ചതും - എം.: എംനെമോസിൻ, 2008. - 288 പേ. : അസുഖം. ജ്യാമിതി. 10-11 ഗ്രേഡുകൾ: വിദ്യാർത്ഥികൾക്കുള്ള പാഠപുസ്തകം വിദ്യാഭ്യാസ സ്ഥാപനങ്ങൾ(അടിസ്ഥാന, പ്രൊഫൈൽ ലെവലുകൾ)

2. Sharygin I.F. - M.: Bustard, 1999. - 208 p.: ill. ജ്യാമിതി. 10-11 ഗ്രേഡുകൾ: പൊതുവിദ്യാഭ്യാസ സ്ഥാപനങ്ങൾക്കുള്ള പാഠപുസ്തകം

3. ഇ.വി.പോട്ടോസ്കുവേവ്, എൽ.ഐ.സ്വാലിച്ച്. - ആറാം പതിപ്പ്, സ്റ്റീരിയോടൈപ്പ്. - എം.: ബസ്റ്റാർഡ്, 008. - 233 പേ. :il. ജ്യാമിതി. ഗ്രേഡ് 10: ഗണിതത്തെക്കുറിച്ചുള്ള ആഴത്തിലുള്ളതും പ്രത്യേകവുമായ പഠനമുള്ള പൊതുവിദ്യാഭ്യാസ സ്ഥാപനങ്ങൾക്കുള്ള പാഠപുസ്തകം

അധിക വെബ് ഉറവിടങ്ങൾ

2. ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ക്രോസ് സെക്ഷൻ എങ്ങനെ നിർമ്മിക്കാം. ഗണിതം ().

3. ഉത്സവം പെഡഗോഗിക്കൽ ആശയങ്ങൾ ().

ടെട്രാഹെഡ്രോണിൻ്റെ അറ്റം, ടെട്രാഹെഡ്രോണിൻ്റെ മുഖങ്ങൾ, ടെട്രാഹെഡ്രോണിൻ്റെ ശിഖരങ്ങൾ, ഉപരിതലം എന്നിവ എങ്ങനെ കണ്ടെത്താം എന്ന വിഷയത്തിൽ വീട്ടിൽ പ്രശ്നങ്ങൾ ഉണ്ടാക്കുക.

1. ജ്യാമിതി. ഗ്രേഡുകൾ 10-11: പൊതുവിദ്യാഭ്യാസ സ്ഥാപനങ്ങളിലെ വിദ്യാർത്ഥികൾക്കുള്ള പാഠപുസ്തകം (അടിസ്ഥാന, പ്രത്യേക തലങ്ങൾ) I. M. സ്മിർനോവ, V. A. സ്മിർനോവ്. - 5-ാം പതിപ്പ്, തിരുത്തി വിപുലീകരിച്ചത് - എം.: Mnemosyne, 2008. - 288 pp.: ill. ടാസ്‌ക്കുകൾ 18, 19, 20 പേജ് 50

2. പോയിൻ്റ് ഇമധ്യ വാരിയെല്ല് എം.എടെട്രാഹെഡ്രോൺ എം.എ.വി.എസ്. പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക ബി, സിഒപ്പം ഇ.

3. ടെട്രാഹെഡ്രോൺ MABC യിൽ, പോയിൻ്റ് M മുഖം AMV യുടേതാണ്, പോയിൻ്റ് P മുഖം BMC യുടേതാണ്, പോയിൻ്റ് K എഡ്ജ് എസിയുടെതാണ്. പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക എം, ആർ, കെ.

4. ഒരു വിമാനത്തോടുകൂടിയ ടെട്രാഹെഡ്രോണിൻ്റെ വിഭജനത്തിൻ്റെ ഫലമായി എന്ത് രൂപങ്ങൾ ലഭിക്കും?

ജോലിയുടെ ലക്ഷ്യം:
സ്പേഷ്യൽ ആശയങ്ങളുടെ വികസനം.
ചുമതലകൾ:
1. വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള നിയമങ്ങൾ അവതരിപ്പിക്കുക.
2. വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള കഴിവുകൾ വികസിപ്പിക്കുക
ടെട്രാഹെഡ്രോണും സമാന്തരപൈപ്പും വ്യത്യസ്തമാണ്
ഒരു കട്ടിംഗ് വിമാനം വ്യക്തമാക്കുന്ന കേസുകൾ.
3. നിയമങ്ങൾ പ്രയോഗിക്കാനുള്ള കഴിവ് വികസിപ്പിക്കുക
പ്രശ്നങ്ങൾ പരിഹരിക്കുമ്പോൾ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നു
വിഷയങ്ങൾ "പോളിഹെദ്ര".

പലതും പരിഹരിക്കാൻ
ജ്യാമിതീയ
ആവശ്യമായ ജോലികൾ
വിഭാഗങ്ങൾ നിർമ്മിക്കുക
ബഹുമുഖം
വിവിധ
വിമാനങ്ങൾ.

ഒരു കട്ടിംഗ് വിമാനം എന്ന ആശയം

സെക്കൻ്റ്
വിമാനം
സമാന്തര പൈപ്പുകളുള്ള
(ടെട്രാഹെഡ്രോൺ)
ഏതെങ്കിലും വിളിച്ചു
വിമാനം, ഇരുവശത്തും
മുതൽ വശങ്ങൾ
ഉള്ളത്
തന്നിരിക്കുന്ന പോയിൻ്റുകൾ
സമാന്തര പൈപ്പുകളുള്ള
(ടെട്രാഹെഡ്രോൺ).

ഒരു പോളിഹെഡ്രോൺ വിഭാഗത്തിൻ്റെ ആശയം

കട്ടിംഗ് വിമാനം
അരികുകൾ കടക്കുന്നു
ടെട്രാഹെഡ്രോൺ
(സമാന്തരമായി) വഴി
സെഗ്മെൻ്റുകൾ.
ബഹുഭുജം, വശങ്ങൾ
ഏത് ഡാറ്റയാണ്
സെഗ്മെൻ്റുകൾ എന്ന് വിളിക്കുന്നു
ടെട്രാഹെഡ്രോണിൻ്റെ ക്രോസ് സെക്ഷൻ
(സമാന്തര പൈപ്പ്).

ഡ്രോയിംഗുകളിൽ നിന്ന് പ്രവർത്തിക്കുന്നു

എത്ര വിമാനങ്ങൾ വരയ്ക്കാം
തിരഞ്ഞെടുത്ത ഘടകങ്ങളിലൂടെ?
നിങ്ങൾ എന്ത് സിദ്ധാന്തങ്ങളും സിദ്ധാന്തങ്ങളും പ്രയോഗിച്ചു?

ഒരു വിഭാഗം നിർമ്മിക്കാൻ
പ്ലോട്ട് പോയിൻ്റുകൾ ആവശ്യമാണ്
സെക്കൻ്റ് കവല
അരികുകളുള്ള വിമാനങ്ങളും
അവയെ സെഗ്മെൻ്റുകളുമായി ബന്ധിപ്പിക്കുക.

വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള നിയമങ്ങൾ

1. നിങ്ങൾക്ക് രണ്ടെണ്ണം മാത്രമേ ബന്ധിപ്പിക്കാൻ കഴിയൂ
ഒന്നിൻ്റെ തലത്തിൽ കിടക്കുന്ന പോയിൻ്റുകൾ
അറ്റങ്ങൾ.
2. കട്ടിംഗ് വിമാനം വിഭജിക്കുന്നു
സമാന്തര മുഖങ്ങൾ
സമാന്തര ഭാഗങ്ങൾ.

വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള നിയമങ്ങൾ

3. മുഖത്തിൻ്റെ തലം അടയാളപ്പെടുത്തിയാൽ
ഉൾപ്പെടുന്ന ഒരു പോയിൻ്റ് മാത്രം
വിഭാഗം തലം, പിന്നെ അത് ആവശ്യമാണ്
ഒരു അധിക പോയിൻ്റ് നിർമ്മിക്കുക.
ഇത് ചെയ്യുന്നതിന്, നിങ്ങൾ പോയിൻ്റുകൾ കണ്ടെത്തേണ്ടതുണ്ട്
ഇതിനകം നിർമ്മിച്ച കവലകൾ
മറ്റ് നേർരേഖകൾക്കൊപ്പം നേർരേഖകൾ,
ഒരേ അരികുകളിൽ കിടക്കുന്നു.

10. ടെട്രാഹെഡ്രോൺ വിഭാഗങ്ങളുടെ നിർമ്മാണം

11.

ഒരു ടെട്രാഹെഡ്രോണിന് 4 മുഖങ്ങളുണ്ട്
വിഭാഗങ്ങളിൽ അത് മാറിയേക്കാം
ത്രികോണങ്ങൾ
ചതുർഭുജങ്ങൾ

12.

ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ക്രോസ് സെക്ഷൻ നിർമ്മിക്കുക
DABC വിമാനം കടന്നുപോകുന്നു
എം, എൻ, കെ പോയിൻ്റുകളിലൂടെ
1. നമുക്ക് ഒരു നേർരേഖ വരയ്ക്കാം
പോയിൻ്റുകൾ എം, കെ, കാരണം അവർ കള്ളം പറയുന്നു
ഒരു മുഖത്ത് (ADC).
ഡി
എം
എ.എ.
എൻ
കെ
ബി.ബി
CC
2. നമുക്ക് ഒരു നേർരേഖ വരയ്ക്കാം
പോയിൻ്റ് കെ, എൻ, കാരണം അവർ
ഒരേ വശത്ത് കിടക്കുക
(സിഡിബി).
3. സമാനമായി വാദിക്കുന്നു,
ഒരു നേർരേഖ MN വരയ്ക്കുക.
4. ത്രികോണം MNK –
ആവശ്യമുള്ള വിഭാഗം.

13. എബിസിക്ക് സമാന്തരമായി എം പോയിൻ്റിലൂടെ കടന്നുപോകുന്നു.

ഡി
1. പോയിൻ്റ് എം വഴി വരയ്ക്കാം
നേരായ സമാന്തര
എഡ്ജ് AB
2.
എം
ആർ
എ
TO
കൂടെ
IN
പോയിൻ്റ് എം വഴി കടന്നുപോകാം
നേരായ സമാന്തര
എഡ്ജ് എസി
3. നമുക്ക് ഒരു നേർരേഖ വരയ്ക്കാം
പോയിൻ്റ് കെ, പി, കാരണം അവർ കിടക്കുന്നു
ഒരു മുഖം (DBC)
4. ത്രികോണ MPK –
ആവശ്യമുള്ള വിഭാഗം.

14.

ഒരു വിമാനം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക,
E, F, K എന്നീ പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്നു.
ഡി
1. ഞങ്ങൾ KF നടപ്പിലാക്കുന്നു.
2. ഞങ്ങൾ FE നടപ്പിലാക്കുന്നു.
3. നമുക്ക് തുടരാം
EF, നമുക്ക് AC തുടരാം.
എഫ്
4.ഇഎഫ് എസി = എം
5. ഞങ്ങൾ നടപ്പിലാക്കുന്നു
എം.കെ.
ഇ
എം
AB=L
6.
എം.കെ
സി
എ
7. EL നടത്തുക
എൽ
EFKL - ആവശ്യമായ വിഭാഗം
കെ
ബി

15.

ഒരു വിമാനം ഉപയോഗിച്ച് ടെട്രാഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക,
E, F, K എന്നീ പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്നു
ഏതൊക്കെ
എന്താണ്
പോയിൻ്റ്,
ഉള്ളിൽ കിടക്കുന്നു
കഴിയും
ബന്ധിപ്പിക്കുക
ഫലമായി
ഏത്
പോയിൻ്റുകൾ
കഴിയും
നേരിട്ട്
എന്ന്
അതേ
അറ്റങ്ങൾ
കഴിയും
തുടരുക,
വരെ
ലഭിക്കും
പോയിൻ്റുകൾ,
കള്ളം പറയുന്നു
വി
ഒന്ന്
ബന്ധിപ്പിക്കണോ?
ബന്ധിപ്പിക്കുക
ലഭിച്ചു
അധിക
പോയിൻ്റ്?
അരികുകൾ,
പേര്
വിഭാഗം.
അധിക പോയിൻ്റ്?
ഡി
എ.സി
ELFK
FSEC
ഒരു ഡോട്ടും
കെ, ഇ
എഫ്.കെ
എഫ്
എൽ
സി
എം
എ
ഇ
കെ
ബി

16.

ഒരു വിഭാഗം നിർമ്മിക്കുക
ടെട്രാഹെഡ്രോൺ വിമാനം,
പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്നു
ഇ, എഫ്, കെ.
ഡി
എഫ്
എൽ
സി
എ
ഇ
കെ
ബി
കുറിച്ച്

17.

ഉപസംഹാരം: രീതി പ്രശ്നമല്ല
നിർമ്മാണ വിഭാഗങ്ങൾ സമാനമാണ്

18. സമാന്തര പൈപ്പ് വിഭാഗങ്ങളുടെ നിർമ്മാണം

19.

ഒരു ടെട്രാഹെഡ്രോണിന് 6 മുഖങ്ങളുണ്ട്
ത്രികോണങ്ങൾ
പെൻ്റഗണുകൾ
അതിൻ്റെ വിഭാഗങ്ങളിൽ അത് മാറിയേക്കാം
ചതുർഭുജങ്ങൾ
ഷഡ്ഭുജങ്ങൾ

20. പ്ലെയിനിന് സമാന്തരമായി X പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു സമാന്തര പൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക (OSV)

IN 1
A1
വൈ
എക്സ്
D1
എസ്
IN
എ
ഡി
Z
1. നമുക്ക് നിങ്ങളെ കടന്നുപോകാം
C1
പോയിൻ്റ് X നേർരേഖ
അരികിൽ സമാന്തരമായി
D1C1
2. പോയിൻ്റ് X വഴി
നേരിട്ട്
അരികിൽ സമാന്തരമായി
D1D
3. പോയിൻ്റ് Z വഴി ഒരു നേർരേഖയുണ്ട്
അരികിൽ സമാന്തരമായി
കൂടെ
ഡിസി
4. നമുക്ക് ഒരു നേർരേഖ വരയ്ക്കാം
പോയിൻ്റ് എസ്, വൈ, കാരണം അവർ കിടക്കുന്നു
ഒരു മുഖം (BB1C1)
XYSZ - ആവശ്യമായ വിഭാഗം

21.

ഒരു സമാന്തര പൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക
പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന വിമാനം
എം,എ,ഡി
IN 1
D1
ഇ
A1
C1
IN
എ
1. എ.ഡി
2. എം.ഡി
3. ME//AD, കാരണം (ABC)//(A1B1C1)
4. എ.ഇ.
5. AEMD - ആവശ്യമായ വിഭാഗം
എം
ഡി
കൂടെ

22. എം, കെ, ടി പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് സമാന്തര പൈപ്പിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക

എൻ
എം
TO
ആർ
എസ്
എക്സ്
ടി

23. ജോലികൾ സ്വയം പൂർത്തിയാക്കുക

എം
ടി
ലേക്ക്
എം
ഡി
ലേക്ക്
ടി
ഇതിൻ്റെ ഒരു വിഭാഗം നിർമ്മിക്കുക: a) ഒരു സമാന്തര പൈപ്പ്;
ബി) ടെട്രാഹെഡ്രോൺ
എം, ടി, കെ പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന വിമാനം.

24. ഉപയോഗിച്ച വിഭവങ്ങൾ

Soboleva L. I. വിഭാഗങ്ങളുടെ നിർമ്മാണം
Tkacheva V.V. വിഭാഗങ്ങളുടെ നിർമ്മാണം
ടെട്രാഹെഡ്രോണും സമാന്തര പൈപ്പും
ഗോബോസോവ L.V. നിർമ്മാണ പ്രശ്നങ്ങൾ
വിഭാഗങ്ങൾ
ഡിവിഡി. കിരിൽ നിന്നുള്ള ജ്യാമിതി പാഠങ്ങളും
മെഥോഡിയസ്. പത്താം ക്ലാസ്, 2005
പരിശീലനവും പരിശോധനയും ജോലികൾ.
ജ്യാമിതി. പത്താം ക്ലാസ് (നോട്ട്ബുക്ക്)/അലെഷിന
ടി.എൻ. – എം.: ഇൻ്റലക്റ്റ്-സെൻ്റർ, 1998

പ്ലാനിമെട്രിയുടെ സിദ്ധാന്തങ്ങൾ:

വ്യത്യസ്ത പാഠപുസ്തകങ്ങളിൽ, ലൈനുകളുടെയും പ്ലെയിനുകളുടെയും സവിശേഷതകൾ വ്യത്യസ്ത രീതികളിൽ അവതരിപ്പിക്കാൻ കഴിയും, ഒരു സിദ്ധാന്തം, അതിൽ നിന്നുള്ള ഒരു പരിണതഫലം, ഒരു സിദ്ധാന്തം, ലെമ്മ മുതലായവ. പോഗോറെലോവ് എ.വിയുടെ പാഠപുസ്തകം പരിഗണിക്കുക.

ഒരു നേർരേഖ ഒരു വിമാനത്തെ രണ്ട് അർദ്ധ-തലങ്ങളായി വിഭജിക്കുന്നു.

ഏത് അർദ്ധ-രേഖയിൽ നിന്നും, തന്നിരിക്കുന്ന അർദ്ധ-തലത്തോടുകൂടിയ ഒരു കോണിനെ ഒരു നിശ്ചിത അർദ്ധ-തലത്തിലേക്ക് പ്ലോട്ട് ചെയ്യാൻ കഴിയും. ഡിഗ്രി അളവ്, 180-ൽ താഴെ 0 , ഒന്നു മാത്രം.

ഒരു ത്രികോണം എന്തുതന്നെയായാലും, നൽകിയിരിക്കുന്ന അർദ്ധരേഖയുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ തന്നിരിക്കുന്ന സ്ഥലത്ത് ഒരു തുല്യ ത്രികോണമുണ്ട്.

തന്നിരിക്കുന്ന വരിയിൽ കിടക്കാത്ത ഒരു പോയിൻ്റിലൂടെ, തന്നിരിക്കുന്ന വരിയ്ക്ക് സമാന്തരമായി ഒരു ലൈൻ വരയ്ക്കാൻ കഴിയും.

സ്റ്റീരിയോമെട്രിയുടെ സിദ്ധാന്തങ്ങൾ:

ഏത് തലം ആയാലും, ഈ തലത്തിന് കീഴിലുള്ള പോയിൻ്റുകളും ഈ തലത്തിന് ചേരാത്ത പോയിൻ്റുകളും അതിൽ പെടാത്ത പോയിൻ്റുകളും ഉണ്ട്.

രണ്ട് വ്യത്യസ്ത തലങ്ങൾക്ക് ഒരു പൊതു പോയിൻ്റുണ്ടെങ്കിൽ, ഈ പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖയിലൂടെ അവ വിഭജിക്കുന്നു.

രണ്ട് വ്യത്യസ്ത വരികൾക്ക് ഒരു പൊതു പോയിൻ്റുണ്ടെങ്കിൽ, അവയിലൂടെ ഒരു വിമാനം വരയ്ക്കാൻ കഴിയും, ഒന്ന് മാത്രം.

ഏത് രേഖയായാലും, ഈ വരിയിൽ ഉൾപ്പെടുന്ന പോയിൻ്റുകളും അതിൽ പെടാത്ത പോയിൻ്റുകളും ഉണ്ട്.

ഏതെങ്കിലും രണ്ട് പോയിൻ്റുകളിലൂടെ നിങ്ങൾക്ക് ഒരു നേർരേഖ വരയ്ക്കാം, ഒന്ന് മാത്രം.

ഒരു ലൈനിലെ മൂന്ന് പോയിൻ്റുകളിൽ ഒന്ന്, മറ്റ് രണ്ട് പോയിൻ്റുകൾക്കിടയിൽ ഒന്ന് മാത്രം.

ഓരോ സെഗ്‌മെൻ്റിനും പൂജ്യത്തേക്കാൾ ഒരു നിശ്ചിത ദൈർഘ്യമുണ്ട്. ഒരു സെഗ്‌മെൻ്റിൻ്റെ നീളം അതിൻ്റെ ഏതെങ്കിലും പോയിൻ്റ് കൊണ്ട് ഹരിച്ചിരിക്കുന്ന ഭാഗങ്ങളുടെ നീളത്തിൻ്റെ ആകെത്തുകയ്ക്ക് തുല്യമാണ്.

ഒരു തലം ഉൾപ്പെടുന്ന ഒരു നേർരേഖ ഈ വിമാനത്തെ രണ്ട് അർദ്ധതലങ്ങളായി വിഭജിക്കുന്നു.

ഓരോ കോണിനും പൂജ്യത്തേക്കാൾ ഒരു നിശ്ചിത ഡിഗ്രി അളവുണ്ട്. നേർകോണ് 180 ആണ് 0 . ഒരു കോണിൻ്റെ ഡിഗ്രി അളവ് അതിൻ്റെ വശങ്ങൾക്കിടയിൽ കടന്നുപോകുന്ന ഏതെങ്കിലും കിരണത്താൽ വിഭജിച്ചിരിക്കുന്ന കോണുകളുടെ ഡിഗ്രി അളവുകളുടെ ആകെത്തുകയ്ക്ക് തുല്യമാണ്.

അതിൻ്റെ ആരംഭ പോയിൻ്റിൽ നിന്ന് ഏത് പകുതി-ലൈനിലും, നിങ്ങൾക്ക് ഒരു നിശ്ചിത ദൈർഘ്യത്തിൻ്റെ ഒരു ഭാഗം പ്ലോട്ട് ചെയ്യാൻ കഴിയും, ഒന്ന് മാത്രം.

അത് ഉൾക്കൊള്ളുന്ന പ്ലെയിനിലെ ഒരു അർദ്ധരേഖയിൽ നിന്ന്, ഒരു നിശ്ചിത ഡിഗ്രി അളവിലുള്ള 180-ൽ താഴെയുള്ള ഒരു കോണിനെ ഒരു നിശ്ചിത അർദ്ധ-തലത്തിലേക്ക് പ്ലോട്ട് ചെയ്യാൻ കഴിയും. 0 , ഒന്നു മാത്രം.

ഏത് ത്രികോണമായാലും, ഒരു നിശ്ചിത സ്ഥലത്ത് ഒരു നിശ്ചിത തലത്തിൽ ആ തലത്തിൽ നൽകിയിരിക്കുന്ന അർദ്ധരേഖയുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ ഒരു തുല്യ ത്രികോണമുണ്ട്.

ഒരു വിമാനത്തിൽ, തന്നിരിക്കുന്ന വരിയിൽ കിടക്കാത്ത ഒരു നിശ്ചിത പോയിൻ്റിലൂടെ, തന്നിരിക്കുന്നതിന് സമാന്തരമായി ഒരു നേർരേഖ വരയ്ക്കാൻ കഴിയും.

വിഭാഗം

ബഹിരാകാശത്ത്, രണ്ട് രൂപങ്ങൾക്ക്, നമ്മുടെ കാര്യത്തിൽ, ഒരു വിമാനത്തിനും ഒരു പോളിഹെഡ്രോണിനും ഇനിപ്പറയുന്ന പരസ്പര ക്രമീകരണം ഉണ്ടായിരിക്കാം: വിഭജിക്കരുത്, ഒരു ബിന്ദുവിൽ വിഭജിക്കുക, ഒരു നേർരേഖയിൽ വിഭജിക്കുക, വിമാനം അതിൻ്റെ ഇൻ്റീരിയർ ഉപയോഗിച്ച് പോളിഹെഡ്രോണിനെ വിഭജിക്കുന്നു (ചിത്രം 1) , അതേ സമയം ഇനിപ്പറയുന്ന കണക്കുകൾ രൂപപ്പെടുത്തുക:

a) ശൂന്യമായ രൂപം (മുറിക്കരുത്)

ബി) പോയിൻ്റ്

സി) സെഗ്മെൻ്റ്

d) ബഹുഭുജം

ഒരു പോളിഹെഡ്രോണിൻ്റെയും ഒരു തലത്തിൻ്റെയും കവലയിൽ ഒരു ബഹുഭുജം ഉണ്ടെങ്കിൽ, ഈ ബഹുഭുജംഒരു വിമാനമുള്ള ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു വിഭാഗത്തെ വിളിക്കുന്നു .

ചിത്രം.1

നിർവ്വചനം. വിഭാഗം സ്‌പേഷ്യൽ ബോഡി (ഉദാഹരണത്തിന്, ഒരു പോളിഹെഡ്രോൺ) ഒരു വിമാനവുമായി ശരീരത്തിൻ്റെ വിഭജനത്തിൻ്റെ ഫലമായുണ്ടാകുന്ന രൂപമാണ്.

കട്ടിംഗ് വിമാനം ബഹുമുഖം നൽകിയിരിക്കുന്ന പോളിഹെഡ്രോണിൻ്റെ പോയിൻ്റുകൾ ഉള്ള ഇരുവശത്തും ഏതെങ്കിലും വിമാനത്തെ വിളിക്കാം.

വിമാനം അതിൻ്റെ ഇൻ്റീരിയറിനൊപ്പം പോളിഹെഡ്രോണിനെ വിഭജിക്കുമ്പോൾ മാത്രമേ ഞങ്ങൾ പരിഗണിക്കൂ. ഈ സാഹചര്യത്തിൽ, പോളിഹെഡ്രോണിൻ്റെ ഓരോ മുഖവുമുള്ള ഈ വിമാനത്തിൻ്റെ വിഭജനം ഒരു നിശ്ചിത സെഗ്മെൻ്റ് ആയിരിക്കും.

വിമാനങ്ങൾ ഒരു നേർരേഖയിൽ വിഭജിക്കുകയാണെങ്കിൽ, നേർരേഖയെ വിളിക്കുന്നുഈ വിമാനങ്ങളിൽ ഒന്നിനെ മറ്റൊന്നിലേക്ക് പിന്തുടരുന്നു.

പൊതുവേ, ഒരു പോളിഹെഡ്രോണിൻ്റെ കട്ടിംഗ് തലം അതിൻ്റെ ഓരോ മുഖത്തിൻ്റെയും തലത്തെ വിഭജിക്കുന്നു (അതുപോലെ ഈ പോളിഹെഡ്രോണിൻ്റെ മറ്റേതെങ്കിലും കട്ടിംഗ് തലം). പോളിഹെഡ്രോണിൻ്റെ അരികുകൾ കിടക്കുന്ന ഓരോ വരികളെയും ഇത് വിഭജിക്കുന്നു.

കട്ടിംഗ് തലം പോളിഹെഡ്രോണിൻ്റെ ഏതെങ്കിലും മുഖത്തിൻ്റെ തലത്തെ വിഭജിക്കുന്ന നേർരേഖയെ വിളിക്കുന്നുകട്ടിംഗ് വിമാനം പിന്തുടരുന്നു ഈ മുഖത്തിൻ്റെ തലത്തിൽ, കട്ടിംഗ് പ്ലെയിൻ പോളിഹെഡ്രോണിൻ്റെ ഏതെങ്കിലും അറ്റം ഉൾക്കൊള്ളുന്ന രേഖയെ വിഭജിക്കുന്ന പോയിൻ്റിനെ വിളിക്കുന്നു.കട്ടിംഗ് വിമാനം പിന്തുടരുന്നു ഓൺഈ നേർരേഖ. കട്ടിംഗ് പ്ലെയിനിലെ ഒരു ലൈനിൻ്റെ ട്രെയ്സ് കൂടിയാണ് ഈ പോയിൻ്റ്. കട്ടിംഗ് പ്ലെയിൻ പോളിഹെഡ്രോണിൻ്റെ മുഖത്തെ നേരിട്ട് വിഭജിക്കുകയാണെങ്കിൽ, മുഖത്തെ കട്ടിംഗ് തലത്തിൻ്റെ അടയാളത്തെക്കുറിച്ചും അതുപോലെ തന്നെ, നമുക്ക് സംസാരിക്കാംപോളിഹെഡ്രോണിൻ്റെ അരികിൽ കട്ടിംഗ് വിമാനത്തിൻ്റെ ട്രെയ്സ്, അതായത്, ഒരു കട്ടിംഗ് പ്ലെയിനിൽ ഒരു എഡ്ജ് ട്രെയ്സ് കുറിച്ച്.

ഒരു നേർരേഖയെ രണ്ട് പോയിൻ്റുകളാൽ അദ്വിതീയമായി നിർണ്ണയിക്കുന്നതിനാൽ, മറ്റേതെങ്കിലും തലത്തിലും, പ്രത്യേകിച്ച്, ഒരു പോളിഹെഡ്രോണിൻ്റെ ഏതെങ്കിലും മുഖത്തിൻ്റെ തലത്തിലും, ഒരു കട്ടിംഗ് പ്ലെയിനിൻ്റെ ട്രെയ്സ് കണ്ടെത്താൻ, വിമാനങ്ങളുടെ രണ്ട് പൊതു പോയിൻ്റുകൾ നിർമ്മിച്ചാൽ മതി.

ഒരു കട്ടിംഗ് വിമാനത്തിൻ്റെ ട്രെയ്‌സ് നിർമ്മിക്കുന്നതിനും, ഈ തലം ഉപയോഗിച്ച് ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുന്നതിനും, പോളിഹെഡ്രോൺ മാത്രമല്ല, കട്ടിംഗ് വിമാനവും വ്യക്തമാക്കണം. സെക്ഷൻ വിമാനത്തിൻ്റെ നിർമ്മാണം ഈ വിമാനത്തിൻ്റെ സവിശേഷതയെ ആശ്രയിച്ചിരിക്കുന്നു. ഒരു വിമാനം നിർവചിക്കുന്നതിനുള്ള പ്രധാന വഴികൾ, പ്രത്യേകിച്ച് ഒരു കട്ടിംഗ് വിമാനം, ഇനിപ്പറയുന്നവയാണ്:

ഒരേ വരിയിൽ കിടക്കുന്ന മൂന്ന് പോയിൻ്റുകൾ;

ഒരു നേർരേഖയും അതിൽ കിടക്കാത്ത ഒരു പോയിൻ്റും;

രണ്ട് സമാന്തര വരകൾ;

വിഭജിക്കുന്ന രണ്ട് വരികൾ;

ഒരു പോയിൻ്റും രണ്ട് വിഭജിക്കുന്ന വരികളും;

ഒരു കട്ടിംഗ് വിമാനം വ്യക്തമാക്കുന്നതിനുള്ള മറ്റ് വഴികളും സാധ്യമാണ്.

അതിനാൽ, പോളിഹെഡ്രയുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള എല്ലാ രീതികളും രീതികളായി വിഭജിക്കാം.

പോളിഹെഡ്രയുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ

സ്റ്റീരിയോമെട്രിയിലെ പോളിഹെഡ്രയുടെ വിഭാഗങ്ങളുടെ രീതി നിർമ്മാണ പ്രശ്നങ്ങളിൽ ഉപയോഗിക്കുന്നു. ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു വിഭാഗം നിർമ്മിക്കാനും വിഭാഗത്തിൻ്റെ തരം നിർണ്ണയിക്കാനുമുള്ള കഴിവിനെ അടിസ്ഥാനമാക്കിയുള്ളതാണ് ഇത്.

പോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിന് മൂന്ന് പ്രധാന രീതികളുണ്ട്:

ആക്സിയോമാറ്റിക് രീതി:

ട്രെയ്സ് രീതി.

സംയോജിത രീതി.

കോർഡിനേറ്റ് രീതി.

കുറിപ്പ് ട്രേസ് രീതിയും സഹായ വിഭാഗ രീതിയും ഇനങ്ങളാണെന്ന്വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള അക്സിയോമാറ്റിക് രീതി.

പോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള ഇനിപ്പറയുന്ന രീതികളും നമുക്ക് വേർതിരിച്ചറിയാൻ കഴിയും:

ഒരു നിശ്ചിത തലത്തിന് സമാന്തരമായി ഒരു നിശ്ചിത പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു തലം കൊണ്ട് ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുന്നു;

തന്നിരിക്കുന്ന മറ്റൊരു വരിക്ക് സമാന്തരമായി ഒരു നിശ്ചിത വരിയിലൂടെ കടന്നുപോകുന്ന ഒരു ഭാഗം നിർമ്മിക്കുന്നു;

രണ്ട് വിഭജിക്കുന്ന വരികൾക്ക് സമാന്തരമായി നൽകിയിരിക്കുന്ന പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു വിഭാഗം നിർമ്മിക്കുന്നു;

ഒരു നിശ്ചിത തലത്തിലേക്ക് ലംബമായി നൽകിയിരിക്കുന്ന ഒരു വരിയിലൂടെ കടന്നുപോകുന്ന ഒരു തലം കൊണ്ട് ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുന്നു;

തന്നിരിക്കുന്ന ഒരു നേർരേഖയ്ക്ക് ലംബമായി ഒരു നിശ്ചിത പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുന്നു.

വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ നിർമ്മിക്കുന്ന പ്രധാന പ്രവർത്തനങ്ങൾ ഒരു തലം ഉപയോഗിച്ച് ഒരു വരിയുടെ വിഭജന പോയിൻ്റ് കണ്ടെത്തുക, രണ്ട് വിമാനങ്ങളുടെ കവലയുടെ രേഖ നിർമ്മിക്കുക, തലത്തിന് സമാന്തരമായി, തലത്തിന് ലംബമായി ഒരു നേർരേഖ നിർമ്മിക്കുക എന്നിവയാണ്. രണ്ട് വിമാനങ്ങളുടെ കവലയുടെ ഒരു രേഖ നിർമ്മിക്കുന്നതിന്, അതിൻ്റെ രണ്ട് പോയിൻ്റുകൾ സാധാരണയായി കണ്ടെത്തി അവയിലൂടെ ഒരു രേഖ വരയ്ക്കുന്നു. ഒരു ലൈനിൻ്റെയും ഒരു തലത്തിൻ്റെയും കവല പോയിൻ്റ് നിർമ്മിക്കുന്നതിന്, തന്നിരിക്കുന്നതിനെ വിഭജിക്കുന്ന ഒരു ലൈൻ കണ്ടെത്തുക. അപ്പോൾ തന്നിരിക്കുന്നതുമായി കണ്ടെത്തിയ വരിയുടെ കവലയിൽ ആവശ്യമുള്ള പോയിൻ്റ് ലഭിക്കും.

ഞങ്ങൾ പട്ടികപ്പെടുത്തിയിരിക്കുന്നവ പ്രത്യേകം പരിഗണിക്കാംപോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ:

ട്രെയ്സ് രീതി.

ട്രെയ്സ് രീതി സ്റ്റീരിയോമെട്രിയുടെ സിദ്ധാന്തങ്ങളെ അടിസ്ഥാനമാക്കിയുള്ളതാണ് (അടിസ്ഥാനമാക്കി), ഒരു സഹായ രേഖ നിർമ്മിക്കുക എന്നതാണ് രീതിയുടെ സാരാംശം, ഇത് ചിത്രത്തിൻ്റെ ഏതെങ്കിലും മുഖത്തിൻ്റെ തലവുമായി കട്ടിംഗ് പ്ലെയിനിൻ്റെ കവലയുടെ വരിയുടെ ചിത്രമാണ്. താഴത്തെ അടിത്തറയുടെ തലം ഉപയോഗിച്ച് കട്ടിംഗ് വിമാനത്തിൻ്റെ കവലയുടെ വരിയുടെ ഒരു ചിത്രം നിർമ്മിക്കുന്നത് ഏറ്റവും സൗകര്യപ്രദമാണ്. ഈ വരികട്ടിംഗ് വിമാനത്തിൻ്റെ പ്രധാന ട്രെയ്സ് എന്ന് വിളിക്കുന്നു . ഒരു ട്രെയ്സ് ഉപയോഗിച്ച്, ചിത്രത്തിൻ്റെ ലാറ്ററൽ അരികുകളിലോ മുഖങ്ങളിലോ സ്ഥിതിചെയ്യുന്ന കട്ടിംഗ് പ്ലെയിനിൻ്റെ പോയിൻ്റുകളുടെ ചിത്രങ്ങൾ നിർമ്മിക്കുന്നത് എളുപ്പമാണ്. ഈ പോയിൻ്റുകളുടെ ചിത്രങ്ങൾ സ്ഥിരമായി ബന്ധിപ്പിക്കുന്നതിലൂടെ, ആവശ്യമുള്ള വിഭാഗത്തിൻ്റെ ഒരു ചിത്രം നമുക്ക് ലഭിക്കും.

അതല്ല ഒരു കട്ടിംഗ് വിമാനത്തിൻ്റെ പ്രധാന ട്രെയ്സ് നിർമ്മിക്കുമ്പോൾ, ഇനിപ്പറയുന്ന പ്രസ്താവന ഉപയോഗിക്കുന്നു.

പോയിൻ്റുകൾ കട്ടിംഗ് പ്ലെയിനിൻ്റെ ഭാഗമാണെങ്കിൽ, ഒരേ നേർരേഖയിൽ കിടക്കുന്നില്ലെങ്കിൽ, അവയുടെ പ്രൊജക്ഷൻ (മധ്യമോ സമാന്തരമോ) പ്രധാനമായി തിരഞ്ഞെടുത്ത വിമാനത്തിലേക്ക്, പോയിൻ്റുകൾ യഥാക്രമം തുടർന്ന് അനുബന്ധ വരികളുടെ വിഭജന പോയിൻ്റുകൾ, അതായത്, പോയിൻ്റുകളും ഒരേ വരിയിൽ കിടക്കുന്നു (ചിത്രം 1, എ, ബി).

ചിത്രം.1.എ ചിത്രം.1.ബി

ഈ നേർരേഖയാണ് കട്ടിംഗ് വിമാനത്തിൻ്റെ പ്രധാന ട്രെയ്സ്. പോയിൻ്റുകൾ പ്രധാന ട്രെയ്‌സിൽ കിടക്കുന്നതിനാൽ, ഇത് നിർമ്മിക്കാൻ ഈ മൂന്നിൽ നിന്ന് രണ്ട് പോയിൻ്റുകൾ കണ്ടെത്തിയാൽ മതി.

സഹായ വിഭാഗങ്ങളുടെ രീതി.

പോളിഹെഡ്രയുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള ഈ രീതി തികച്ചും സാർവത്രികമാണ്. കട്ടിംഗ് വിമാനത്തിൻ്റെ ആവശ്യമുള്ള ട്രെയ്സ് (അല്ലെങ്കിൽ ട്രെയ്സ്) ഡ്രോയിംഗിന് പുറത്തുള്ള സന്ദർഭങ്ങളിൽ, ഈ രീതിക്ക് ചില ഗുണങ്ങളുണ്ട്. അതേസമയം, ഈ രീതി ഉപയോഗിച്ച് നടത്തുന്ന നിർമ്മാണങ്ങൾ പലപ്പോഴും "തിരക്കേറിയതായി" മാറുന്നുവെന്നത് ഓർമിക്കേണ്ടതാണ്. എന്നിരുന്നാലും, ചില സന്ദർഭങ്ങളിൽ സഹായ വിഭാഗങ്ങളുടെ രീതി ഏറ്റവും യുക്തിസഹമായി മാറുന്നു.

സംയോജിത രീതി

പോളിഹെഡ്രയുടെ വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള സംയോജിത രീതിയുടെ സാരാംശം, ആക്സിയോമാറ്റിക് രീതിയുമായി സംയോജിച്ച് ബഹിരാകാശത്ത് ലൈനുകളുടെയും വിമാനങ്ങളുടെയും സമാന്തരതയെക്കുറിച്ചുള്ള സിദ്ധാന്തങ്ങളുടെ പ്രയോഗമാണ്.

വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള കോർഡിനേറ്റ് രീതി.

കോർഡിനേറ്റ് രീതിയുടെ സാരാംശം, അറ്റങ്ങൾ അല്ലെങ്കിൽ പോളിഹെഡ്രോണുകളുടെ കവല പോയിൻ്റുകളുടെ കോർഡിനേറ്റുകൾ കട്ടിംഗ് പ്ലെയിൻ ഉപയോഗിച്ച് കണക്കാക്കുക എന്നതാണ്, ഇത് വിമാനത്തിൻ്റെ സമവാക്യം വ്യക്തമാക്കുന്നു. പ്രശ്ന സാഹചര്യങ്ങളെ അടിസ്ഥാനമാക്കിയാണ് കട്ടിംഗ് പ്ലെയിൻ സമവാക്യം കണക്കാക്കുന്നത്.

കുറിപ്പ് , ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു വിഭാഗം നിർമ്മിക്കുന്ന ഈ രീതി ഒരു കമ്പ്യൂട്ടറിന് സ്വീകാര്യമാണ്, കാരണം ഇത് വലിയ അളവിലുള്ള കണക്കുകൂട്ടലുകളുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു, അതിനാൽ ഈ രീതി ഒരു കമ്പ്യൂട്ടർ ഉപയോഗിച്ച് നടപ്പിലാക്കുന്നത് ഉചിതമാണ്.

ഒരു വിമാനം ഉപയോഗിച്ച് ഒരു പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കുക എന്നതാണ് ഞങ്ങളുടെ പ്രധാന ദൌത്യം, അതായത്. ഈ രണ്ട് സെറ്റുകളുടെ കവല നിർമ്മിക്കുന്നതിൽ.

പോളിഹെഡ്രയുടെ വിഭാഗങ്ങളുടെ നിർമ്മാണം

ഒന്നാമതായി, ഒരു കോൺവെക്സ് പോളിഹെഡ്രോണിൻ്റെ ഒരു ഭാഗം ഒരു കുത്തനെയുള്ള പരന്ന ബഹുഭുജമാണെന്ന് ഞങ്ങൾ ശ്രദ്ധിക്കുന്നു, ഇതിൻ്റെ ലംബങ്ങൾ, പൊതുവേ, കട്ടിംഗ് പ്ലെയിനിനെ പോളിഹെഡ്രോണിൻ്റെ അരികുകളുള്ള വിഭജന പോയിൻ്റുകളും അതിൻ്റെ വശങ്ങളുമാണ്. മുഖങ്ങൾ.

വിഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള ഉദാഹരണങ്ങൾ:

ഒരു വിഭാഗം നിർവചിക്കുന്നതിനുള്ള രീതികൾ വളരെ വൈവിധ്യപൂർണ്ണമാണ്. അവയിൽ ഏറ്റവും സാധാരണമായത് ഒരേ നേർരേഖയിൽ കിടക്കാത്ത മൂന്ന് പോയിൻ്റുകളാൽ ഒരു കട്ടിംഗ് വിമാനം നിർവചിക്കുന്ന രീതിയാണ്.

ഉദാഹരണം 1. സമാന്തര പൈപ്പ് എബിസിഡിഎയ്ക്ക് 1 ബി 1 സി 1 ഡി 1 . M, N, L പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു വിഭാഗം നിർമ്മിക്കുക.

പരിഹാരം:

AA വിമാനത്തിൽ കിടക്കുന്ന പോയിൻ്റുകൾ M, L എന്നിവ ബന്ധിപ്പിക്കുക 1 ഡി 1 ഡി.

ML (വിഭാഗത്തിൽ പെട്ടത്) എന്ന രേഖയെ A എഡ്ജ് ഉപയോഗിച്ച് നമുക്ക് വിഭജിക്കാം 1 ഡി 1 1 ഡി 1 D. പോയിൻ്റ് X നേടുക 1 .

പോയിൻ്റ് X1 എ അറ്റത്ത് കിടക്കുന്നു 1 ഡി 1 , അതിനാൽ വിമാനം എ 1 ബി 1 സി 1 ഡി 1 , അതേ വിമാനത്തിൽ കിടക്കുന്ന ഒരു തുന്നൽ N ഉപയോഗിച്ച് ഞങ്ങൾ അതിനെ ബന്ധിപ്പിക്കുന്നു.

എക്സ് 1 N വിഭജിക്കുന്നു എ എഡ്ജ് 1 ബി 1 പോയിൻ്റിൽ കെ.

AA എന്ന ഒരേ വിമാനത്തിൽ കിടക്കുന്ന പോയിൻ്റുകൾ K, M എന്നിവ ബന്ധിപ്പിക്കുക 1 ബി 1 ബി.

ഡിഡി പ്ലെയിനിനൊപ്പം സെക്ഷൻ പ്ലെയിനിൻ്റെ കവലയുടെ നേർരേഖ നമുക്ക് കണ്ടെത്താം 1 സി 1 സി:

എഡ്ജ് DD ഉപയോഗിച്ച് ML (വിഭാഗത്തിൽ പെട്ടത്) എന്ന വരിയെ നമുക്ക് വിഭജിക്കാം 1 , അവർ ഒരേ വിമാനത്തിൽ കിടക്കുന്നു AA 1 ഡി 1 ഡി, നമുക്ക് പോയിൻ്റ് X ലഭിക്കും 2 .

KN (വിഭാഗത്തിൽ പെട്ടത്) എന്ന രേഖയെ D എന്ന അരികിൽ നമുക്ക് വിഭജിക്കാം 1 സി 1 , അവർ ഒരേ വിമാനത്തിൽ എയിൽ കിടക്കുന്നു 1 ബി 1 സി 1 ഡി 1 , നമുക്ക് പോയിൻ്റ് X3 ലഭിക്കും;

പോയിൻ്റുകൾ X2, X3 എന്നിവ DD വിമാനത്തിൽ കിടക്കുന്നു 1 സി 1 C. ഒരു നേർരേഖ X വരയ്ക്കുക 2 എക്സ് 3 , സി എഡ്ജിനെ വിഭജിക്കുന്നു 1 പോയിൻ്റ് ടിയിൽ സി, പോയിൻ്റ് പിയിൽ എഡ്ജ് ഡിസി. കൂടാതെ എബിസിഡി തലത്തിൽ കിടക്കുന്ന പോയിൻ്റുകൾ എൽ, പി എന്നിവ ബന്ധിപ്പിക്കുക.

അതിനാൽ, പോളിഹെഡ്രോണിൻ്റെ മുഖങ്ങളെ വിമാനം വിഭജിക്കുന്ന എല്ലാ സെഗ്‌മെൻ്റുകളും കണ്ടെത്തിയാൽ പ്രശ്നം പരിഹരിച്ചതായി കണക്കാക്കുന്നു, അതാണ് ഞങ്ങൾ ചെയ്തത്. MKNTPL - ആവശ്യമായ വിഭാഗം.

കുറിപ്പ്. സമാന്തര വിമാനങ്ങളുടെ സ്വത്ത് ഉപയോഗിച്ച് ഒരു വിഭാഗം നിർമ്മിക്കുന്നതിനുള്ള ഇതേ പ്രശ്നം പരിഹരിക്കാൻ കഴിയും.

മുകളിൽ പറഞ്ഞവയിൽ നിന്ന്, ഇത്തരത്തിലുള്ള പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിന് നിങ്ങൾക്ക് ഒരു അൽഗോരിതം (നിയമം) സൃഷ്ടിക്കാൻ കഴിയും.

പോളിഹെഡ്രയുടെ ഭാഗങ്ങൾ നിർമ്മിക്കുന്നതിനുള്ള നിയമങ്ങൾ:

ഉദാഹരണം 2. ഡിഎൽ, എം

ആക്സിയോമാറ്റിക് രീതി ഉപയോഗിച്ച് നമുക്ക് പരിഹരിക്കാം:

നമുക്ക് ഒരു സഹായ വിമാനം വരയ്ക്കാംഡി.കെ.എം, AB, BC എന്നീ അരികുകളെ E പോയിൻ്റുകളിൽ വിഭജിക്കുന്നുഎഫ്(ചിത്രം 2 ലെ പരിഹാരത്തിൻ്റെ പുരോഗതി.). ഈ ഓക്സിലറി പ്ലെയിനിൽ സെക്ഷൻ പ്ലെയിനിൻ്റെ മുഖ്യമന്ത്രിയുടെ ഒരു "ട്രേസ്" നിർമ്മിക്കാം, CM, E എന്നിവയുടെ വിഭജന പോയിൻ്റ് കണ്ടെത്തുക.എഫ്– പോയിൻ്റ് പി. പോയിൻ്റ് പി, പോലെഎൽ, എബിസി തലത്തിൽ കിടക്കുന്നു, കൂടാതെ സെക്ഷൻ തലം എബിസി തലത്തെ വിഭജിക്കുന്ന ഒരു നേർരേഖ വരയ്ക്കാൻ കഴിയും (എബിസി തലത്തിലെ വിഭാഗത്തിൻ്റെ "ട്രേസ്").

ഉദാഹരണം 3. MABCD പിരമിഡിൻ്റെ അരികുകളിൽ AB, AD എന്നിവയിൽ, ഈ അരികുകളുടെ മധ്യബിന്ദുകളായ യഥാക്രമം P, Q എന്നീ പോയിൻ്റുകൾ ഞങ്ങൾ നിർവചിക്കുന്നു, കൂടാതെ MC യുടെ അരികിൽ R ഒരു പോയിൻ്റ് നിർവചിക്കുന്നു. നമുക്ക് പിരമിഡിൻ്റെ ഒരു ഭാഗം ഒരു തലം കടന്നുപോകുന്നു. പോയിൻ്റുകൾ P, Q, R.

സംയോജിത രീതി ഉപയോഗിച്ച് ഞങ്ങൾ പരിഹാരം നടപ്പിലാക്കും:

1). PQR വിമാനത്തിൻ്റെ പ്രധാന അടയാളം നേർരേഖ PQ ആണെന്ന് വ്യക്തമാണ്.

2). MAC തലം PQ എന്ന നേർരേഖയെ വിഭജിക്കുന്ന പോയിൻ്റ് K കണ്ടെത്താം. K, R എന്നീ പോയിൻ്റുകൾ PQR തലത്തിലും MAC തലത്തിലും പെടുന്നു. അതിനാൽ, KR എന്ന നേർരേഖ വരയ്ക്കുന്നതിലൂടെ, ഈ വിമാനങ്ങളുടെ കവലയുടെ രേഖ നമുക്ക് ലഭിക്കും.

3). നമുക്ക് N=AC BD എന്ന പോയിൻ്റ് കണ്ടെത്താം, MN എന്ന നേർരേഖ വരച്ച് F=KR MN എന്ന പോയിൻ്റ് കണ്ടെത്താം.

4). PQR, MDB എന്നീ പ്ലെയിനുകളുടെ ഒരു പൊതു ബിന്ദുവാണ് പോയിൻ്റ് എഫ്, അതായത്, ഈ വിമാനങ്ങൾ എഫ് പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖയിലൂടെ വിഭജിക്കുന്നു. എന്നിരുന്നാലും, PQ മുതൽ - മധ്യനിരത്രികോണം ABD, പിന്നെ PQ BD ന് സമാന്തരമാണ്, അതായത് PQ എന്ന രേഖ MDB വിമാനത്തിന് സമാന്തരമാണ്. PQ എന്ന നേർരേഖയിലൂടെ കടന്നുപോകുന്ന PQR തലം, PQ എന്ന നേർരേഖയ്ക്ക് സമാന്തരമായ ഒരു നേർരേഖയിലൂടെ MDB എന്ന തലത്തെ വിഭജിക്കുന്നു, അതായത് BD ന് സമാന്തരമായും നേർരേഖയായും. അതിനാൽ, പോയിൻ്റ് എഫ് വഴിയുള്ള MDB വിമാനത്തിൽ നമ്മൾ BD രേഖയ്ക്ക് സമാന്തരമായി ഒരു രേഖ വരയ്ക്കുന്നു.

5). കൂടുതൽ നിർമ്മാണങ്ങൾ ചിത്രത്തിൽ നിന്ന് വ്യക്തമാണ്. തൽഫലമായി, നമുക്ക് PQD "RB" എന്ന ബഹുഭുജം ലഭിക്കും - ആവശ്യമുള്ള വിഭാഗം

പ്രിസത്തിൻ്റെ ക്രോസ് സെക്ഷനുകൾ നമുക്ക് പരിഗണിക്കാം ലാളിത്യത്തിനായി, അതായത്, ലോജിക്കൽ ചിന്തയുടെ സൗകര്യത്തിനായി, നമുക്ക് ക്യൂബിൻ്റെ വിഭാഗങ്ങൾ പരിഗണിക്കാം (ചിത്രം 3.a):

അരി. 3.എ

വശത്തെ അരികുകൾക്ക് സമാന്തരമായി തലങ്ങളുള്ള ഒരു പ്രിസത്തിൻ്റെ ഭാഗങ്ങൾ സമാന്തരരേഖകളാണ്. പ്രത്യേകിച്ച്, ഡയഗണൽ വിഭാഗങ്ങൾ സമാന്തരരേഖകളാണ് (ചിത്രം 4).

ഡെഫ്. ഡയഗണൽ വിഭാഗം ഒരേ മുഖത്ത് ഉൾപ്പെടാത്ത രണ്ട് വശങ്ങളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം വഴി ഒരു പ്രിസം മുറിക്കുന്നു.

ഒരു പ്രിസത്തിൻ്റെ ഡയഗണൽ വിഭാഗത്തിൽ നിന്ന് ഉണ്ടാകുന്ന ബഹുഭുജം ഒരു സമാന്തരരേഖയാണ്. ഡയഗണൽ വിഭാഗങ്ങളുടെ എണ്ണത്തെക്കുറിച്ചുള്ള ചോദ്യംഎൻ-ആംഗിൾ പ്രിസം ഡയഗണലുകളുടെ എണ്ണത്തെക്കാൾ ബുദ്ധിമുട്ടാണ്. അടിഭാഗത്ത് വികർണ്ണങ്ങൾ ഉള്ളതുപോലെ നിരവധി വിഭാഗങ്ങൾ ഉണ്ടാകും. ഒരു കുത്തനെയുള്ള പ്രിസത്തിന് അതിൻ്റെ അടിത്തട്ടിൽ കുത്തനെയുള്ള ബഹുഭുജങ്ങളും ഒരു കോൺവെക്സ് പ്രിസവും ഉണ്ടെന്ന് നമുക്കറിയാം.എൻഡയഗണലുകളുടെ ഗോൺ. അതിനാൽ ഡയഗണലുകളുടെ പകുതി ഡയഗണൽ വിഭാഗങ്ങളുണ്ടെന്ന് നമുക്ക് പറയാം.

കുറിപ്പ്: ചിത്രത്തിൽ ഒരു സമാന്തരപൈപ്പിൻ്റെ ഭാഗങ്ങൾ നിർമ്മിക്കുമ്പോൾ, ഒരു കട്ടിംഗ് പ്ലെയിൻ ചില സെഗ്‌മെൻ്റുകളിൽ രണ്ട് വിപരീത മുഖങ്ങളെ വിഭജിക്കുകയാണെങ്കിൽ, ഈ സെഗ്‌മെൻ്റുകൾ സമാന്തരമാണ് “ഒരു സമാന്തര പൈപ്പിൻ്റെ സ്വത്ത് അനുസരിച്ച്, അതായത്. സമാന്തര പൈപ്പിൻ്റെ വിപരീത മുഖങ്ങൾ സമാന്തരവും തുല്യവുമാണ്.

പതിവായി ചോദിക്കുന്ന ചോദ്യങ്ങൾക്ക് ഞങ്ങൾ ഉത്തരം നൽകും:

ഒരു ക്യൂബ് ഒരു വിമാനം കൊണ്ട് മുറിക്കുമ്പോൾ ലഭിക്കുന്ന ബഹുഭുജങ്ങൾ ഏതാണ്?

"ത്രികോണം, ചതുരം, പഞ്ചഭുജം, ഷഡ്ഭുജം."

ഒരു ക്യൂബ് ഒരു വിമാനം കൊണ്ട് ഒരു ഹെപ്‌റ്റഗണിലേക്ക് മുറിക്കാൻ കഴിയുമോ? അഷ്ടഭുജത്തിൻ്റെ കാര്യമോ?

"ഒന്നും കഴിയില്ല".

3) ചോദ്യം ഉയർന്നുവരുന്നു: ഒരു പോളിഹെഡ്രോൺ ഒരു വിമാനം ഉപയോഗിച്ച് മുറിക്കുന്നതിലൂടെ ലഭിക്കുന്ന ബഹുഭുജത്തിൻ്റെ ഏറ്റവും വലിയ വശങ്ങൾ ഏതാണ്?

ഒരു പോളിഹെഡ്രോൺ ഒരു തലം ഉപയോഗിച്ച് മുറിക്കുന്നതിലൂടെ ലഭിക്കുന്ന ബഹുഭുജത്തിൻ്റെ ഏറ്റവും വലിയ വശങ്ങൾ പോളിഹെഡ്രോണിൻ്റെ മുഖങ്ങളുടെ എണ്ണത്തിന് തുല്യമാണ്. .

ഉദാഹരണം 3. പ്രിസം എയുടെ ഒരു ക്രോസ് സെക്ഷൻ നിർമ്മിക്കുക 1 ബി 1 സി 1 ഡി 1 M, N, K എന്നീ മൂന്ന് പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു വിമാനം വഴി ABCD.

പ്രിസത്തിൻ്റെ ഉപരിതലത്തിൽ എം, എൻ, കെ പോയിൻ്റുകളുടെ സ്ഥാനം നമുക്ക് പരിഗണിക്കാം (ചിത്രം 5).

കേസ് പരിഗണിക്കുക: ബി ഈ സാഹചര്യത്തിൽവ്യക്തമായും M1 = B1.

നിർമ്മാണം:

ഉദാഹരണം 4. സമാന്തര പൈപ്പ് എബിസിഡിഎയുടെ ഒരു വിഭാഗം നിർമ്മിക്കുക 1 ബി 1 സി 1 ഡി 1 M, N, P പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം (പോയിൻ്റുകൾ ഡ്രോയിംഗിൽ സൂചിപ്പിച്ചിരിക്കുന്നു (ചിത്രം 6)).

പരിഹാരം:

അരി. 6

പോയിൻ്റുകൾ N, P എന്നിവ സെക്ഷൻ തലത്തിലും സമാന്തരപൈപ്പിൻ്റെ താഴത്തെ അടിത്തറയുടെ തലത്തിലും കിടക്കുന്നു. ഈ പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖ നിർമ്മിക്കാം. ഈ നേർരേഖയാണ് സമാന്തരപൈപ്പിൻ്റെ അടിത്തറയുടെ തലത്തിലേക്ക് കട്ടിംഗ് വിമാനത്തിൻ്റെ ട്രെയ്സ്.

സമാന്തര പൈപ്പിൻ്റെ AB ഏത് വശത്താണ് കിടക്കുന്നത് എന്ന നേർരേഖ നമുക്ക് തുടരാം. ലൈനുകൾ AB, NP എന്നിവ ചില ഘട്ടങ്ങളിൽ വിഭജിക്കുന്നു S. ഈ പോയിൻ്റ് സെക്ഷൻ പ്ലെയിനിൻ്റെതാണ്.

പോയിൻ്റ് M എന്നതും സെക്ഷൻ പ്ലെയിനിൽ പെടുന്നതിനാൽ AA രേഖയെ വിഭജിക്കുന്നു 1 ചില ഘട്ടങ്ങളിൽ X.

X, N പോയിൻ്റുകൾ AA മുഖത്തിൻ്റെ ഒരേ തലത്തിലാണ് കിടക്കുന്നത് 1 ഡി 1 ഡി, അവയെ ബന്ധിപ്പിച്ച് നേർരേഖ XN നേടുക.

സമാന്തരപൈപ്പിൻ്റെ മുഖങ്ങളുടെ തലങ്ങൾ സമാന്തരമായതിനാൽ, പോയിൻ്റ് M വഴി നമുക്ക് A മുഖത്തേക്ക് ഒരു നേർരേഖ വരയ്ക്കാം. 1 ബി 1 സി 1 ഡി 1 , വരി NP ന് സമാന്തരമായി. ഈ ലൈൻ ബി വശത്തെ വിഭജിക്കും 1 കൂടെ 1 പോയിൻ്റ് Y.

അതുപോലെ, ഞങ്ങൾ നേർരേഖ XN-ന് സമാന്തരമായി YZ വരയ്ക്കുന്നു. ഞങ്ങൾ Z-യെ പിയുമായി ബന്ധിപ്പിച്ച് ആവശ്യമുള്ള വിഭാഗം നേടുക - MYZPNX.

ഒരു പിരമിഡിൻ്റെ അഗ്രത്തിലൂടെ കടന്നുപോകുന്ന വിമാനങ്ങളുടെ ഭാഗങ്ങൾ ത്രികോണങ്ങളാണ്. പ്രത്യേകിച്ച്, ത്രികോണങ്ങൾ ഡയഗണൽ വിഭാഗങ്ങളാണ്. പിരമിഡിൻ്റെ രണ്ട് നോൺ-അടുത്തുള്ള ലാറ്ററൽ അറ്റങ്ങളിലൂടെ കടന്നുപോകുന്ന വിമാനങ്ങളുടെ വിഭാഗങ്ങളാണിവ.

ഉദാഹരണം 4. പിരമിഡ് എബിസിയുടെ ഒരു ഭാഗം നിർമ്മിക്കുകഡികെ പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന വിമാനം,എൽ, എം.

പരിഹാരം:

ഇതേ ഉദാഹരണം നമുക്ക് വ്യത്യസ്തമായി പരിഹരിക്കാം .

പോയിൻ്റുകളിൽ K എന്ന് നമുക്ക് അനുമാനിക്കാം,എൽ, എം നിർമ്മിച്ച വിഭാഗംകെ.എൽ.എൻ.എം(ചിത്രം 7). എന്ന് നമുക്ക് സൂചിപ്പിക്കാംഎഫ്ഒരു ചതുർഭുജത്തിൻ്റെ ഡയഗണലുകളുടെ വിഭജന പോയിൻ്റ്കെ.എൽ.എൻ.എം. നമുക്ക് നേരിട്ട് ഉണ്ടാക്കാംഡി.എഫ്കൂടാതെ സൂചിപ്പിക്കുകഎഫ് 1 എബിസിയുടെ അരികിലുള്ള അതിൻ്റെ കവല പോയിൻ്റ്. ഡോട്ട്എഫ് 1 AM, SC എന്നീ നേർരേഖകളുടെ വിഭജന പോയിൻ്റുമായി യോജിക്കുന്നു (എഫ് 1 ഒരേസമയം AM വിമാനങ്ങളുടേതാണ്ഡിഒപ്പംഡിഎസ്.കെ). ഫുൾ സ്റ്റോപ്പ്എഫ് 1 നിർമ്മിക്കാൻ എളുപ്പമാണ്. അടുത്തതായി ഞങ്ങൾ ഒരു പോയിൻ്റ് നിർമ്മിക്കുന്നുഎഫ്കവലയുടെ ഒരു പോയിൻ്റായിഡി.എഫ് 1 ഒപ്പംഎൽ.എം.. അടുത്തതായി നമ്മൾ പോയിൻ്റ് കണ്ടെത്തുന്നുഎൻ.

പരിഗണിക്കപ്പെടുന്ന സാങ്കേതികതയെ വിളിക്കുന്നുആന്തരിക ഡിസൈൻ രീതി . (ഞങ്ങളുടെ കാര്യത്തിന് ഞങ്ങൾ സംസാരിക്കുന്നത്കേന്ദ്ര രൂപകൽപ്പനയെക്കുറിച്ച്. ചതുർഭുജംകെMSA എന്നത് ഒരു ചതുർഭുജത്തിൻ്റെ പ്രൊജക്ഷൻ ആണ്കെ.എം.എൻ.എൽപോയിൻ്റിൽ നിന്ന്ഡി. ഈ സാഹചര്യത്തിൽ, ഡയഗണലുകളുടെ വിഭജന പോയിൻ്റ്കെ.എം.എൻ.എൽ- ഡോട്ട്എഫ്- ചതുർഭുജത്തിൻ്റെ ഡയഗണലുകളുടെ വിഭജന പോയിൻ്റിലേക്ക് പോകുന്നുകെMSA - പോയിൻ്റ്എഫ് 1 .

ഒരു പോളിഹെഡ്രോണിൻ്റെ സെക്ഷണൽ ഏരിയ.

ഒരു പോളിഹെഡ്രോണിൻ്റെ ക്രോസ്-സെക്ഷണൽ ഏരിയ കണക്കാക്കുന്നതിനുള്ള പ്രശ്നം സാധാരണയായി നിരവധി ഘട്ടങ്ങളിൽ പരിഹരിക്കപ്പെടുന്നു. ഒരു വിഭാഗം നിർമ്മിച്ചതായി പ്രശ്നം പ്രസ്താവിക്കുന്നുവെങ്കിൽ (അല്ലെങ്കിൽ ഒരു കട്ടിംഗ് വിമാനം വരച്ചിരിക്കുന്നു, മുതലായവ), പരിഹാരത്തിൻ്റെ ആദ്യ ഘട്ടത്തിൽ വിഭാഗത്തിൽ ലഭിച്ച രൂപത്തിൻ്റെ തരം നിർണ്ണയിക്കപ്പെടുന്നു.

ക്രോസ്-സെക്ഷണൽ ഏരിയ കണക്കാക്കുന്നതിനുള്ള ഉചിതമായ ഫോർമുല തിരഞ്ഞെടുക്കുന്നതിന് ഇത് ചെയ്യണം. വിഭാഗത്തിൽ ലഭിച്ച രൂപത്തിൻ്റെ തരം വ്യക്തമാക്കുകയും ഈ ചിത്രത്തിൻ്റെ വിസ്തീർണ്ണം കണക്കാക്കുന്നതിനുള്ള ഒരു ഫോർമുല തിരഞ്ഞെടുക്കുകയും ചെയ്ത ശേഷം, ഞങ്ങൾ നേരിട്ട് കമ്പ്യൂട്ടേഷണൽ ജോലിയിലേക്ക് പോകുന്നു.

ചില സന്ദർഭങ്ങളിൽ, വിഭാഗത്തിൽ ലഭിച്ച രൂപത്തിൻ്റെ തരം കണ്ടെത്താതെ, സിദ്ധാന്തത്തിൽ നിന്ന് പിന്തുടരുന്ന ഫോർമുല ഉപയോഗിച്ച് അതിൻ്റെ വിസ്തീർണ്ണം കണക്കാക്കാൻ നിങ്ങൾ നേരിട്ട് പോയാൽ അത് എളുപ്പമായിരിക്കും.

ഒരു ബഹുഭുജത്തിൻ്റെ ഓർത്തോഗണൽ പ്രൊജക്ഷൻ്റെ വിസ്തൃതിയെക്കുറിച്ചുള്ള സിദ്ധാന്തം: ഒരു തലത്തിലേക്ക് ഒരു ബഹുഭുജത്തിൻ്റെ ഓർത്തോഗണൽ പ്രൊജക്ഷൻ്റെ വിസ്തീർണ്ണം അതിൻ്റെ വിസ്തീർണ്ണത്തിൻ്റെ ഉൽപ്പന്നത്തിനും പോളിഗോണിൻ്റെ തലവും പ്രൊജക്ഷൻ തലവും തമ്മിലുള്ള കോണിൻ്റെ കോസൈനും തുല്യമാണ്: .

സെക്ഷണൽ ഏരിയ കണക്കാക്കുന്നതിനുള്ള ശരിയായ സൂത്രവാക്യം ഇതാണ്: വിഭാഗത്തിൽ ലഭിച്ച ചിത്രത്തിൻ്റെ ഓർത്തോഗണൽ പ്രൊജക്ഷൻ്റെ വിസ്തീർണ്ണം എവിടെയാണ്, ഇത് കട്ടിംഗ് പ്ലെയിനിനും ചിത്രം പ്രദർശിപ്പിച്ചിരിക്കുന്ന തലത്തിനും ഇടയിലുള്ള കോണാണ്. ഈ പരിഹാരം ഉപയോഗിച്ച്, വിഭാഗത്തിൽ ലഭിച്ച ചിത്രത്തിൻ്റെ ഒരു ഓർത്തോഗണൽ പ്രൊജക്ഷൻ നിർമ്മിക്കുകയും കണക്കുകൂട്ടുകയും ചെയ്യേണ്ടത് ആവശ്യമാണ്

ഒരു വിഭാഗം നിർമ്മിക്കേണ്ടതുണ്ടെന്നും തത്ഫലമായുണ്ടാകുന്ന വിഭാഗത്തിൻ്റെ വിസ്തീർണ്ണം കണ്ടെത്തേണ്ടതുണ്ടെന്നും പ്രശ്ന പ്രസ്താവന പ്രസ്താവിക്കുന്നുവെങ്കിൽ, ആദ്യ ഘട്ടത്തിൽ ഒരാൾ ന്യായമായ രീതിയിൽ തന്നിരിക്കുന്ന ഭാഗം നിർമ്മിക്കണം, തുടർന്ന്, സ്വാഭാവികമായും, അതിൽ ലഭിച്ച രൂപത്തിൻ്റെ തരം നിർണ്ണയിക്കണം. വിഭാഗം മുതലായവ.

ഇനിപ്പറയുന്ന വസ്തുത നമുക്ക് ശ്രദ്ധിക്കാം: കോൺവെക്സ് പോളിഹെഡ്രയുടെ വിഭാഗങ്ങൾ നിർമ്മിച്ചിരിക്കുന്നതിനാൽ, സെക്ഷൻ പോളിഗോണും കുത്തനെയുള്ളതായിരിക്കും, അതിനാൽ അതിനെ ത്രികോണങ്ങളായി വിഭജിച്ച് അതിൻ്റെ വിസ്തീർണ്ണം കണ്ടെത്താനാകും, അതായത്, വിഭാഗത്തിൻ്റെ വിസ്തീർണ്ണം പ്രദേശങ്ങളുടെ ആകെത്തുകയ്ക്ക് തുല്യമാണ്. അത് രചിച്ചിരിക്കുന്ന ത്രികോണങ്ങൾ.

ടാസ്ക് 1.

– അടിത്തറയുടെ ഒരു വശം തുല്യവും ഉയരത്തിന് തുല്യവുമായ ഒരു സാധാരണ ത്രികോണ പിരമിഡ്, പിരമിഡിൻ്റെ ഒരു ഭാഗം നിർമ്മിച്ച്, വശത്തിൻ്റെ മധ്യത്തിലുള്ള പോയിൻ്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു തലം ഉപയോഗിച്ച് അതിൻ്റെ വിസ്തീർണ്ണം കണ്ടെത്തുക (ചിത്രം 8).

പരിഹാരം.

പിരമിഡിൻ്റെ ക്രോസ് സെക്ഷൻ ഒരു ത്രികോണമാണ്. നമുക്ക് അതിൻ്റെ പ്രദേശം കണ്ടെത്താം.

പിരമിഡിൻ്റെ അടിസ്ഥാനം ഒരു സമഭുജ ത്രികോണവും പോയിൻ്റ് വശത്തിൻ്റെ മധ്യഭാഗവുമായതിനാൽ, അത് ഉയരവും തുടർന്ന്, .

ഒരു ത്രികോണത്തിൻ്റെ വിസ്തീർണ്ണം കണ്ടെത്താം:

ടാസ്ക് 2.

ഒരു സാധാരണ പ്രിസത്തിൻ്റെ ലാറ്ററൽ എഡ്ജ് അടിത്തറയുടെ വശത്തിന് തുല്യമാണ്. ഒരു ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന വിമാനങ്ങൾ ഉപയോഗിച്ച് പ്രിസത്തിൻ്റെ ഭാഗങ്ങൾ നിർമ്മിക്കുകഎ, നേർരേഖയ്ക്ക് ലംബമായി, പ്രിസത്തിൻ്റെ ഫലമായുണ്ടാകുന്ന ക്രോസ്-സെക്ഷൻ്റെ വിസ്തീർണ്ണം ഞങ്ങൾ കണ്ടെത്തുകയാണെങ്കിൽ.

പരിഹാരം.

നമുക്ക് നൽകിയിരിക്കുന്ന വിഭാഗം നിർമ്മിക്കാം. നമുക്ക് ഇത് പൂർണ്ണമായും ജ്യാമിതീയ പരിഗണനകളിൽ നിന്ന് ചെയ്യാം, ഉദാഹരണത്തിന്, ഇനിപ്പറയുന്നത്.

തന്നിരിക്കുന്ന ഒരു വരിയിലൂടെയും ഒരു നിശ്ചിത പോയിൻ്റിലൂടെയും കടന്നുപോകുന്ന ഒരു തലത്തിൽ, ഈ പോയിൻ്റിലൂടെ വരിയിലേക്ക് ലംബമായി ഒരു രേഖ വരയ്ക്കുക (ചിത്രം 9). ഈ ആവശ്യത്തിനായി, നമുക്ക് ത്രികോണത്തിൽ എന്ന വസ്തുത ഉപയോഗിക്കാം അതായത്, അതിൻ്റെ മധ്യവും ഈ ത്രികോണത്തിൻ്റെ ഉയരമാണ്. അതിനാൽ ഇത് നേരെയാണ്.

പോയിൻ്റിലൂടെ ഞങ്ങൾ വരിയിലേക്ക് ലംബമായി മറ്റൊരു രേഖ വരയ്ക്കുന്നു. നമുക്ക് അത് വരയ്ക്കാം, ഉദാഹരണത്തിന്, ഒരു നേർരേഖയിലൂടെ കടന്നുപോകുന്ന ഒരു വിമാനത്തിൽ. ഈ രേഖ നേർരേഖയാണെന്ന് വ്യക്തമാണ്

അതിനാൽ, ലൈനിന് ലംബമായി രണ്ട് വിഭജിക്കുന്ന വരികൾ നിർമ്മിച്ചിരിക്കുന്നു. ഈ ലൈനുകൾ ലൈനിന് ലംബമായി ഒരു പോയിൻ്റിലൂടെ കടന്നുപോകുന്ന ഒരു തലം നിർവചിക്കുന്നു, അതായത്, ഒരു സെക്കൻ്റ് തലം വ്യക്തമാക്കിയിരിക്കുന്നു.

ഈ വിമാനം ഉപയോഗിച്ച് നമുക്ക് പ്രിസത്തിൻ്റെ ഒരു ഭാഗം നിർമ്മിക്കാം. അതിനാൽ, ലൈൻ വിമാനത്തിന് സമാന്തരമാണെന്നത് ശ്രദ്ധിക്കുക. അപ്പോൾ നേർരേഖയിലൂടെ കടന്നുപോകുന്ന തലം, നേർരേഖയ്ക്ക് സമാന്തരമായ ഒരു നേർരേഖയിലൂടെ, അതായത് ഒരു നേർരേഖയിലൂടെ വിമാനത്തെ വിഭജിക്കുന്നു. നമുക്ക് പോയിൻ്റിലൂടെ ഒരു നേർരേഖ വരയ്ക്കാം, തത്ഫലമായുണ്ടാകുന്ന പോയിൻ്റിനെ ഒരു ഡോട്ട് ഉപയോഗിച്ച് ബന്ധിപ്പിക്കാം.

ചതുർഭുജം നൽകിയിരിക്കുന്ന വിഭാഗം. നമുക്ക് അതിൻ്റെ പ്രദേശം നിർണ്ണയിക്കാം.