Sekcijos statyba. Mokslinis darbas tema "daugiakampių pjūvių konstravimo metodai"

29.09.2019

Ankstesnėse užduotyse mums pakako teorijos žinių, kad sukonstruotume skersinį pjūvį. Panagrinėkime kitą problemą. Užduotis 1. Sukonstruoti tetraedro, einančio per tašką M, atkarpą, lygiagrečią plokštumai ABD. M Vienas taškas mums niekaip nepadės, tačiau problema turi papildomą sąlygą: atkarpa turi būti lygiagreti plokštumai ABD. Ką tai mums duoda? 1. Plokštumos ADB ir DBC susikerta išilgai tiesės DB, todėl atkarpa, lygiagreti ADB, kerta DBC išilgai (Jei dvi lygiagrečios tiesės lygiagrečios DB. plokštumos kertasi su trečdaliu, tai susikirtimo linijos lygiagrečios) M taškas M priklauso susidurti su DBC. Per ją N nubrėžkime tiesę MK, lygiagrečią su DB. 2. Panašiai: (ADB) (ABC)=AB, K todėl atkarpa susikirs (ABC) tiesia linija, lygiagrečia AB. K(ABC). Per tašką K plokštumoje ABC nubrėžkite tiesę KN, lygiagrečią su AB. M N K N (ADC), M (ADC), todėl MN (ADC) (ir pjovimo plokštumos). Atlikime NM. MKN yra reikalingas skyrius. Taigi: M N 1. Konstrukcija: 1. Plokštumoje (DBC) MK // DB, MK BC = K. 2. Plokštumoje (ABC) KN // AB, KN AC = N. 3. MN Įrodykime, kad MKN yra reikalingas skyrius K 2. Įrodymas. 1. Atkarpa eina per tašką M 2. N (ADC), M (ADC) => NM (ADC) 3. MK // DB, NK // AB pagal konstrukciją, todėl (NMK) // (ABD) pagal atributas. Todėl MKN yra norima b.t.c. 2 uždavinys. Sukurkite gretasienio ABCDA1B1C1D1 pjūvį, einantį per briaunos D1C1 vidurį ir tašką D, lygiagrečią tiesei a. B1 C1 samprotavimas. M A1 D1 B A C D 1. Pažymėkite sąlygoje nurodytą tašką (vadinkime jį savavališkai). M – D1C1 vidurys. 2. Taškai M ir D yra B1 C1 M A1 A, vadinasi, juos galima sujungti. D1 B C D toje pačioje plokštumoje DD1C1, Daugiau nėra ko jungti. 3. Naudokime papildomą sąlygą: pjovimo plokštuma turi būti lygiagreti tiesei a. B1 C1 M A1 B C S A Norėdami tai padaryti, joje turi būti tiesė, lygiagreti tiesei a. Lengviausias būdas yra nubrėžti tokią tiesią liniją ABC plokštumoje, nes jame yra tiesė a ir taškas D, priklausantis atkarpai. D ABC plokštumoje per tašką D nubrėžkite tiesę DS, lygiagrečią tiesei a. DS AB = S. 4. Kadangi (ABC) // (A1B1C1), nubrėžti plokštumoje (A1B1C1), per tašką M, tiesė MP // SD. MP B1C1 = P 5. Kadangi (DD1C1) // (AA1B1), tada P B C plokštumoje (AA1B1) per tašką S galime nubrėžti tiesę M N A D SN lygiagrečią DM. SN BB1 = N 1 1 1 1 B C S A D 6. Taškai N ir P yra plokštumoje (A1B1C1). Sujunkime juos. SNPMD – reikalingas skyrius. Taigi: 1. Statyba. 1. MD B1 A1 N P C1 S A M 3. Į (A1B1C1), per tašką M, MP // DS, MP B1C1 = P C 4. Plokštumoje (AA1B1), per tašką S, SN // DM, SN BB1 = N 5. NP D1 B D 2. In (ABC), per tašką D, DS // a, DS AB = S Įrodykime, kad SNPMD yra reikalingas skyrius. 2. Įrodymas. B1 A1 N 1. Atkarpa eina per tašką D ir briaunos D1C1 vidurį - tašką M. P C1 M C S A 3. PM // SD, P B1C1 pagal konstrukciją D1 B D 2. DS // a, (S AB) pagal konstrukciją, todėl (KNP) // a pagal požymį. 4. SN // DM, N BB1 pagal konstrukciją 5. P (BB1C1), N (BB1C1) => PN (BB1C1). Todėl SNPMD yra norimas skerspjūvis ir kt. 3 uždavinys. Sukurkite gretasienio atkarpą, lygiagrečią B1A ir einančią per taškus M ir N. Samprotavimas. 1. Sujunkite M ir N (jie yra plokštumoje (C1A1B1)). B1 N M A1 D1 B A C1 C D Daugiau nėra ko jungti. Naudokime papildomą sąlygą: pjovimo plokštuma turi būti lygiagreti tiesei B1A 2. Kad pjovimo plokštuma būtų lygiagreti su AB1, būtina, kad joje būtų tiesė, lygiagreti AB1 (arba DC1, nes DC // AB1 by gretasienio savybė). Patogiausia tokią tiesią liniją pavaizduoti veide DD1C1C, nes (DD1C1) // (AA1B1) ir AB1 (AA1B1). Plokštumoje (DD1C1) nubrėžkime tiesę NK // AB1, NK DD1 = K. B1 N M A1 D1 B 3. Dabar plokštumoje AA1D1 yra du pjūviui priklausantys taškai M ir K. Sujunkime juos. C K A C1 D MNK – reikiama atkarpa. Taigi: 1. Statyba. 1. MN 2. Plokštumoje (DD1C1) NK // AB1, NK DD1 = K. . B1 N A1 A M D1 C1 3. MK Įrodykime, kad MNK yra reikiamas skyrius 2. Įrodymas. B C 1. Atkarpa eina per taškus M ir N. K 2. M (A1B1C1), N (A1B1C1) => D MN (A1B1C1). 3. M (ADD1), K (ADD1) => MK (ADD1). 4. Nes NK // AB1 pagal konstrukciją, tada (MNK) // AB1 pagal tiesės ir plokštumos lygiagretumą. Todėl MNK yra norima b.t.c. 3 užduotis. 1. Tetraedre DABC sukonstruokite atkarpą su plokštuma, einančia per briaunos DC vidurį, viršūnę B ir lygiagrečią tiesei AC. 2. Sukonstruokite gretasienio pjūvį, kurio plokštuma eina per briaunos B1C1 vidurį ir tašką K, esantį ant briaunos CD, lygiagrečią tiesei BD, jei DK: KC = 1: 3. M 3. Sukonstruokite tetraedro pjūvį su plokštuma, einanti per taškus M ir C, lygiagreti tiesi a (1 pav.). 1 pav. 4. Lygiagretaus vamzdžio ABCDA1B1C1D1 taškas E priklauso kraštinei CD. Sukurkite gretasienio atkarpą su plokštuma, einančia per šį tašką ir lygiagrečiai plokštumai BC1D. 5. Sukurkite gretasienio atkarpą su plokštuma, einančia per AA1, lygiagrečią MN, kur M yra AB vidurio taškas, N - BC vidurio taškas. 6. Sukurkite gretasienio atkarpą su plokštuma, einančia per briaunos B1C1 vidurį, lygiagrečią plokštumai AA1C1.

ŠVIETIMO, MOKSLO MINISTERIJAIR KRYMO RESPUBLIKOS JAUNIMAS

MAŽOJI MOKSLŲ AKADEMIJA „IEŠKOJAS“

Katedra: matematika

Skyrius: matematika

DAUGIAKEDRINIŲ SEKCIJŲ KONSTRUKCIJOS METODAI

Aš padariau darbą:

_______________

klasės mokinys

Mokslinis patarėjas:

Santraukos

Daugiakampių pjūvių konstravimo metodai

Katedra: matematika

Skyrius: matematika

Mokslinis patarėjas:

Tyrimo tikslas yra įvairių daugiabriaunių atkarpų konstravimo metodų tyrimas. Už tai irbuvo išnagrinėta teorinė medžiaga šia tema, susisteminti ruožų konstravimo uždavinių sprendimo metodai, pateikti kiekvieno metodo taikymo uždavinių pavyzdžiai, nagrinėjami uždavinių pavyzdžiai vieningame valstybiniame atkarpų konstravimo ir jų elementų skaičiavimo egzamine.

ĮVADAS………………………………………………………………………………….3

1 SKYRIUS. DAUGIAKEDRINIŲ PRIEŽIŪRIŲ KONSTRUKCIJA, PAGRINDAS SEREOMETRIJOS AKSIOMINE SISTEMA…………………………………………………………4

2 SKYRIUS. PĖDĖKIMO METODAS KONSTRUKCIJOS DALYKIEDRŲ SEKCIJAS…………………………………………………………………………………10

3 SKYRIUS. VIDAUS PROJEKTAVIMO METODAS

POLIEDŲ SEKCIJŲ STATYBA…………………………14

4 SKYRIUS. KOMBINUOTAS SEKCIJŲ STATYBOS METODAS

POLYhedra…………………………………………………………17

5 SKYRIUS. KOORDINACINIS METODAS KONSTRUKCIJŲ POLIHEDIJŲ SKYRIUS………………………………………………………………………………….19

IŠVADA………………………………………………………………25

NUORODOS…………………………………………………………………………………………………………………………………………………………………………………………………

ĮVADAS

Absolventai turės laikyti matematikos egzaminą, o tam būtinos žinios ir gebėjimas spręsti stereometrines problemas, rašyti šį egzaminąmaksimalaus balo. Aktualumas Šis darbas susijęs su būtinybe savarankiškai ruoštis egzaminui, o nagrinėjama tema yra viena svarbiausių.

A demo analizė, diagnostika ir mokymas Vieningo valstybinio egzamino parinktys Su 2009-2014 m parodė, kad 70 proc. geometrines užduotis sudaro atkarpų konstravimo ir jų elementų skaičiavimo užduotys– kampai, plotai.

IN mokymo planas skiriamos daugiabriaunių atkarpų konstravimo užduotys 2 akademinės valandos, ko neužtenka šiai temai nagrinėti. Mokykloje daugiakampių plokštumos pjūviai konstruojami tik remiantis stereometrijos aksiomomis ir teoremomis. Tuo pačiu metu yra ir kitų plokščių daugiakampių dalių konstravimo būdų. Veiksmingiausi yra pėdsakų metodas, vidinio projektavimo metodas ir kombinuotas metodas. Labai įdomus ir daug žadantis sprendimo pritaikymo požiūriu įvairios užduotys koordinačių metodas. Jei daugiakampis patalpintas į koordinačių sistemą, o pjovimo plokštuma nurodyta lygtimi, tada atkarpos konstravimas bus sumažintas iki plokštumos susikirtimo su daugiakampio kraštinėmis taškų koordinačių radimo.

Studijų objektas: Daugiakampių atkarpų konstravimo metodai.

Tyrimo tikslas: studijuoti įvairių metodų daugiabriaunių atkarpų konstravimas.

Tyrimo tikslai:

1) Studijuokite teorinę medžiagą šia tema.

2) Susisteminti atkarpų statybos uždavinių sprendimo būdus.

3) Pateikite kiekvieno metodo užduočių pavyzdžių.

4) Apsvarstykite Vieningo valstybinio egzamino problemų pavyzdžius konstruojant atkarpas ir skaičiuojant jų elementus.

1 SKYRIUS

DAUGIAKEDRINIŲ SEKCIJŲ STATYBA

PAGRĮSTA SEREOMETRIJOS AKSIOMOS SISTEMA

Apibrėžimas. Vadinamas daugiakampio pjūvis plokštuma geometrinė figūra, kuri yra visų erdvės taškų, vienu metu priklausančių tam tikram daugiakampiui ir plokštumai, rinkinys; plokštuma vadinama pjovimo plokštuma.

Daugiakampio paviršius susideda iš briaunų – atkarpų ir paviršių – plokščių daugiakampių. Kadangi tiesė ir plokštuma susikerta taške, o dvi plokštumos susikerta išilgai tiesės, tai daugiakampio pjūvis plokštuma yra plokštumos daugiakampis; šio daugiakampio viršūnės yra pjovimo plokštumos susikirtimo taškai su daugiakampio briaunomis, o kraštinės yra atkarpos, išilgai kurių pjovimo plokštuma kerta savo paviršius. Tai reiškia, kad sukonstruoti norimą tam tikro daugiakampio atkarpą su plokštuma α užtenka sukonstruoti jo susikirtimo taškus su daugiakampio kraštinėmis. Tada sujunkite šiuos taškus iš eilės segmentais.

Pjovimo plokštumą α galima nurodyti: trimis taškais, kurie nėra toje pačioje tiesėje; tiesi linija ir jai nepriklausantis taškas; kitos sąlygos, lemiančios jo padėtį tam tikro daugiakampio atžvilgiu. Pavyzdžiui, 1 pav. keturkampės piramidės PABCD pjūvis sudarytas iš plokštumos α, apibrėžtos taškais M, K ir H, atitinkamai priklausančiais kraštams PC, PD ir PB;

1 pav

Užduotis. Lygiagrečiame ABC DA 1 B 1 C 1 D 1 sukonstruoti atkarpą plokštuma, einantis per viršūnes C ir D 1 ir atkarpos B 1 taškas K C 1 (2 pav., a).

Sprendimas. 1. T. Į . SU ∈ DD 1 C 1, D 1 ∈ DD 1 C 1, tada pagal aksiomą (per du taškus, priklausantis lėktuvui, eina per tiesią liniją, ir tik vienas) sukonstruokime pėdsaką CD 1 plokštumoje DD 1 C 1 (2 pav., b).

2. Panašiai ir A plokštumoje 1 B 1 C 1 sukonstruosime pėdsaką DK, plokštumoje BB 1 C 1 sukonstruosime pėdsaką CK.

3. D 1 KC – norimą skyrių (pav..2, c)

a B C)

2 pav

Užduotis. Sukonstruoti piramidės RABC atkarpą su plokštuma α = (MKH), kur M, K ir H yra atitinkamai briaunų RS, PB ir AB vidiniai taškai (3 pav., a).

Sprendimas. 1 žingsnis. Taškai M ir K yra kiekvienoje iš dviejų plokštumų α ir RVS. Todėl pagal dviejų plokštumų susikirtimo aksiomą α plokštuma kerta RVS plokštumą išilgai tiesės MK. Vadinasi, segmentas MK yra viena iš norimos sekcijos pusių (3 pav., b).

2 žingsnis. Panašiai segmentas KN yra kita norimos sekcijos pusė (3 pav., c).

3 žingsnis. Taškai M ir H nėra vienu metu nė vienoje piramidės RABC paviršiuje, todėl atkarpa MH nėra šios piramidės atkarpos pusė. Tiesios linijos KN ir RA yra AVR veido plokštumoje ir susikerta. Sukonstruokime tašką T= KH ∩AP (3 pav., d).

Kadangi tiesė KN yra α plokštumoje, tai taškas T yra α plokštumoje. Dabar matome, kad plokštumos α ir APC turi bendrus taškus M ir T. Vadinasi, pagal dviejų plokštumų susikirtimo aksiomą plokštuma α ir plokštuma APC susikerta išilgai tiesės MT, kuri, savo ruožtu, kerta kraštą AC taške R (3 pav., e). .

4-as žingsnis. Dabar, kaip ir 1 veiksme, nustatome, kad plokštuma α kerta ACP ir ABC veidus atitinkamai išilgai segmentų MR ir HR. Vadinasi, reikalinga atkarpa yra keturkampis MKHR (3 pav., f).

3 pav

Panagrinėkime sudėtingesnę problemą.

Užduotis . Sukurkite penkiakampės piramidės PABCDE atkarpą plokštuma

α = (KQR), kur K, Q yra atitinkamai kraštinių RA ir RS vidiniai taškai, o taškas R yra paviršiaus DPE viduje (4 pav., a).

Sprendimas . Tiesės QK ir AC yra toje pačioje plokštumoje ACP (pagal tiesės ir plokštumos aksiomą) ir susikerta tam tikrame taške T 1 , (4 pav.,b), o T 1 є α, nes QК є α.

Tiesė PR kerta DE tam tikrame taške F (4 pav., c), kuris yra piramidės pagrindo plokštumos ARR ir kraštinės DE susikirtimo taškas. Tada tiesės KR ir AF yra toje pačioje plokštumoje ARR ir susikerta tam tikrame taške T 2 (4 pav., d), o T 2 є α , kaip tiesės KR є α taškas (pagal tiesės ir plokštumos aksiomą).

Gauta: tiesiai T 1 T 2 yra skersinėje plokštumoje α ir piramidės pagrindo plokštumoje (pagal tiesės ir plokštumos aksiomą), o tiesė kerta atitinkamai piramidės pagrindo ABCDE kraštines DE ir AE, taškuose M ir N (4 pav., e), kurie yra plokštumos α susikirtimo su piramidės briaunomis DE ir AE taškai ir tarnauja kaip norimos atkarpos viršūnės.

Be to, tiesė MR yra veido DPE plokštumoje ir pjovimo plokštumoje α (pagal tiesės ir plokštumos aksiomą), o kerta kraštą PD tam tikrame taške H - kita norimos atkarpos viršūnė. (4 pav., f).

Toliau pastatykime tašką T 3 – T 1 T 2 ∩ AB (4 pav., g), kuris, kaip tiesės T taškas 1 T 2 є α, guli plokštumoje a (pagal tiesės ir plokštumos aksiomą). Dabar veido RAB plokštuma priklauso dviem taškams T 3 ir į pjovimo plokštumą α, o tai reiškia tiesę T 3 K yra šių plokštumų susikirtimo tiesi linija. Tiesus T 3 K kerta kraštą PB taške L (4 pav., h), kuris tarnauja kaip kita norimos atkarpos viršūnė.

Taigi norimos sekcijos konstravimo sekos „grandinė“ yra tokia:

1. T 1 = QK∩ AC ; 2. F = PR ∩ DE;

3. T 2 = KR ∩ AF; 4. M = T 1 T 2 ∩ DE;

5.N= T 1 T 2 ∩ AE ; 6. N = MR ∩ PD;

7.T 3 = T 1 T 2 ∩ AB ; 8.L=T 3 K ∩ PB.

Šešiakampis MNKLQH yra reikalinga sekcija.

4 pav

Naudojant lygiagrečių plokštumų savybes, galima sukonstruoti daugiakampio pjūvį su lygiagrečiais paviršiais (prizmė, gretasienis kubas).

Užduotis . Taškai M, P ir R yra gretasienio kraštinėse. Naudodamiesi lygiagrečių tiesių ir plokštumų savybėmis, sukonstruokite šio gretasienio atkarpą pagal MPR plokštumą.

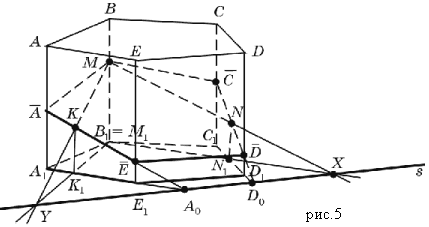
Sprendimas. Tegul taškai M, P ir R yra atitinkamai DD kraštinėse 1, BB 1 ir SS 1 gretasienis ABCBA 1 B 1 C 1 B 1 (5 pav., a).

Pažymime: (MPR) = α - pjovimo plokštuma. Nubrėžiame segmentus MR ir PR (5 pav., b), išilgai kurių plokštuma α kerta atitinkamai paviršius CC 1 D 1 D ir BB 1 C 1 Iš šio gretasienio. Segmentai MR ir PR yra norimos sekcijos pusės. Toliau naudojame teoremas apie dviejų lygiagrečių plokštumų susikirtimą su trečiąja.

Kadangi veidas AA yra 1 B 1 B yra lygiagreti veidui CC 1 D 1 D, tada plokštumos α susikirtimo tiesė su veido AA plokštuma 1 iš 1 B turi būti lygiagreti tiesei MR. Todėl nubrėžiame atkarpą PQ || MR, Q є AB (5 pav., c); segmentas PQ yra kita norimos sekcijos pusė. Panašiai, nes veidas AA 1 D 1 D yra lygiagreti veidui CC 1 iš 1 B, tada plokštumos α susikirtimo tiesė su veido AA plokštuma 1 D 1 D turi būti lygiagreti tiesei PR. Todėl nubrėžiame atkarpą MH || PR, H = AD (5 pav., c); segmentas MH yra kita norimos sekcijos pusė. Veido ABCD kraštinėse AB ir AD buvo sukonstruoti taškai Q є AB ir H є AD, kurie yra norimos atkarpos viršūnės. Nubrėžiame atkarpą QH ir gauname penkiakampį MRPQH – norimą gretasienio atkarpą.

a B C)

Ryžiai. 5

2 SKYRIUS

ATĖKIMO METODAS KONSTRUKCIJOS DALYKIEDRŲ SEKCIJAS

Apibrėžimas. Tiesi linija, išilgai kurios pjovimo plokštuma α kerta daugiakampio pagrindo plokštumą, vadinama plokštumos α pėdsaku šio pagrindo plokštumoje.

Iš pėdsako apibrėžimo gauname: kiekviename jo taške susikerta tiesės, kurių viena yra slenkančioje plokštumoje, kita – pagrindo plokštumoje. Būtent ši pėdsako savybė naudojama konstruojant daugiakampio plokštumos pjūvius trasos metodu. Šiuo atveju pjovimo plokštumoje patogu naudoti tiesias linijas, kurios kerta daugiakampio kraštus.

Pirmiausia apibrėžiame sekantinę plokštumą pagal jos pėdsaką prizmės (piramidės) pagrindo plokštumoje ir tašku, priklausančiu prizmės (piramidės) paviršiui.

Užduotis. Sukurkite ABCVEA prizmės skerspjūvį 1 B 1 C 1 D 1 E 1 plokštuma α, kuri pateikiama taipl prizmės pagrindo plokštumoje ABC ir briaunai DD priklausančio taško M 1 (7 pav., a).

Sprendimas. Analizė. Tarkime, kad penkiakampis MNPQR yra norima atkarpa (6 pav.). Norint sukonstruoti šį plokščią penkiakampį, pakanka pastatyti jo viršūnes N, P, Q, R (duotas taškas M) - pjovimo plokštumos α susikirtimo taškus su briaunomis, atitinkamai CC. 1, BB 1, AA 1, EE 1 šios prizmės.

Ryžiai. 6

Sukonstruoti tašką N = α ∩ СС 1 pakanka nubrėžti pjovimo plokštumos α susikirtimo tiesę su veido СDD plokštuma 1 C 1 . Tam, savo ruožtu, užtenka šio veido plokštumoje sukonstruoti kitą tašką, priklausantį pjovimo plokštumai α. Kaip sukurti tokį tašką?

Kadangi jis yra tiesus l yra prizmės pagrindo plokštumoje, tada ji gali susikirsti su veido CDD plokštuma 1 C 1 tik taške, kuris priklauso eilutei CD = (CDD 1 ) ∩ (ABC), t.y. taškas X =l∩CD = l∩ (CDD 1 ) priklauso pjovimo plokštumai α. Taigi, norint sukurti tašką N = α ∩ СС 1 užtenka sukonstruoti tašką X =l ∩CD. Panašiai statyti taškus P = α ∩ BB 1, Q = α ∩ AA 1 ir R = α ∩ EE 1 pakanka atitinkamai sukonstruoti taškus: Y =l∩ BC, Z = l∩ AB ir T = l∩ AE. Iš čia

Statyba.

X = l∩ CD (7 pav., b);

N = MX ∩ СС 1 (7 pav., b);

Y = l∩ BC (7 pav., c);

P = NY ∩ BB 1 (7 pav., c);

Z= l∩ AB (7 pav., c);

Q= PZ ∩ AA 1 (7 pav., d);

T = l∩ AE (6 pav.);

R= QT ∩ EE 1 (6 pav.).

Pentagon MNPQR yra reikalinga sekcija (6 pav.).

Įrodymas . Kadangi jis yra tiesus l yra pjovimo plokštumos α pėdsakas, tada taškai X =l∩ СD, Y = l∩ BC, Z = l∩ AB ir T= l ∩ AE priklauso šiai plokštumai.

Todėl mes turime:

М є α , X є α => МХ є α, tada МХ ∩ СС 1 = N є α, o tai reiškia N = α ∩ СС 1 ;

N є α, Y є α => NY є α, tada NY ∩ ВВ 1 = Р є α, o tai reiškia Р = α ∩ ВВ 1 ;

Р є α, Z є α => РZ є α, tada PZ ∩ AA 1 = Q є α, vadinasi, Q = α ∩ AA 1 ;

Q є α, T є α => QТ є α, tada QТ ∩ EE 1 =R є α, vadinasi, R = α ∩ Е 1 .

Todėl MNPQR yra reikalinga sekcija.

a) b)

c) d)

Ryžiai. 7

Studijuoti. Trasa l pjovimo plokštuma α nekerta prizmės pagrindo, o pjovimo plokštumos taškas M priklauso šoninei briaunai DD 1 prizmės. Todėl pjovimo plokštuma α nėra lygiagreti šoninėms briaunoms. Vadinasi, šios plokštumos susikirtimo su prizmės šoninėmis briaunomis (arba šių briaunų plėtiniais) taškai N, P, Q ir R visada egzistuoja. Ir kadangi, be to, taškas M nepriklauso pėdsakuil , tada jų apibrėžta plokštuma α yra unikali. Tai reiškia, kad problema turi unikalų sprendimą.

Užduotis. Sukurkite penkiakampės piramidės PABCDE atkarpą naudodami toliau pateiktą plokštumąl ir krašto PE vidinis taškas K.

Sprendimas. Schematiškai norimos sekcijos konstrukcija gali būti pavaizduota taip (8 pav.): T 1 → Q → T 2 → R → T 3 → M → T 4 → N.

Pentagon MNKQR yra reikalinga sekcija.

Atkarpos viršūnių konstravimo sekos „grandinė“ yra tokia:

1. T 1 = l∩ AE; 2. Q = T 1 K ∩ RA;

3. T 2 = l∩ AB; 4. R = T 2 Q ∩ РВ;

5. T 3 = l∩ BC; 6. M = T 3 R ∩ RS;

7. T 4 = l∩CD; 8. N = T 4 M ∩ РD.

Ryžiai. 8

Pjovimo plokštuma dažnai apibrėžiama trimis taškais, priklausančiais daugiakampiui. Šiuo atveju, norėdami sukurti norimą atkarpą trasos metodu, pirmiausia sukonstruokite pjovimo plokštumos pėdsaką nurodyto daugiakampio pagrindo plokštumoje.

3 SKYRIUS

INTERJERAUS PROJEKTAVIMO METODAS

DAUGIAKEDRINIŲ SEKCIJŲ STATYBA

Vidaus projektavimo metodas dar vadinamas korespondencijos metodu arba įstrižinių pjūvių metodu.

Taikant šį metodą, kiekvienas duotas taškas projektuojamas į pagrindinę plokštumą. Yra du galimi tipai dizainas: centrinis ir lygiagretus. Centrinė projekcija paprastai naudojama statant piramidžių dalis, o piramidės viršūnė yra projekcijos centras. Konstruojant prizmių pjūvius naudojamas lygiagretusis dizainas.

Užduotis . Sukonstruoti piramidės PABCDE atkarpą su plokštuma α = (MFR), jei taškai M, F ir R yra atitinkamai briaunų RA, RS ir PE vidiniai taškai (9 pav., a).

Sprendimas . Piramidės pagrindo plokštumą pažymėkime β. Norint sukonstruoti norimą atkarpą, sukonstruojame pjovimo plokštumos α susikirtimo taškus su piramidės kraštinėmis.

Sukonstruokime pjovimo plokštumos susikirtimo tašką su šios piramidės briauna PD.

Plokštumos APD ir CPE kerta plokštumą β atitinkamai išilgai tiesių AD ir CE, kurios susikerta tam tikrame taške K (9 pav., c). Tiesė PK=(APD) ∩(CPE) tam tikrame taške K kerta tiesę FR є α 1 Į 1 = RK ∩ FR (9 pav., d), o K 1 є α. Tada: M є α, K 1 є α => tiesi linija MK є a. Todėl taškas Q = MK 1 ∩ PD (9 pav., e) – briaunos PD ir pjovimo plokštumos susikirtimo taškas: Q = α ∩ PD. Taškas Q yra norimos atkarpos viršūnė. Panašiai sukonstruojame plokštumos α ir briaunos PB susikirtimo tašką. Plokštumos BPE ir АD kerta plokštumą β atitinkamai išilgai tiesių BE ir AD, kurios susikerta taške H (9 pav., e). Tiesi linija PH = (BPE) ∩ (APD) kerta tiesią MQ taške H 1 (9 pav., g). Tada tiesi linija RN 1 kerta briauną PB taške N = α ∩ PB - atkarpos viršūnė (9 pav., h).

1. K = AD ∩ EC; 2. K 1 = RK ∩ RF;

3.Q= MK 1 ∩ R D; 4. H = BE ∩ A D;

5. Н 1 = РН ∩ МQ; 6. N = RН 1 ∩ РВ.

Pentagon MNFQR yra reikalinga sekcija (9 pav., i).

a B C)

kur)

g) h) i)

Ryžiai. 9

Užduotis . Sukurkite prizmės ABCDEA skerspjūvį 1 B 1 C 1 D 1 E 1 , plokštuma α, apibrėžta taškais M є BB 1, P DD 1, Q EE 1 (10 pav.).

Sprendimas. Pažymime: β - prizmės apatinio pagrindo plokštumą. Norint sukurti norimą atkarpą, sukonstruojame plokštumos α = (MPQ) susikirtimo taškus su prizmės kraštinėmis.

Sukonstruokime plokštumos α susikirtimo tašką su briauna AA 1 .

Plokštumos A 1 AD ir BEE 1 kerta plokštumą β išilgai tiesių AD ir BE atitinkamai, kurios susikerta tam tikrame taške K. Kadangi plokštumos A 1 AD ir BEE 1 pereiti per lygiagrečias briaunas AA 1 ir BB 1 prizmės ir turi bendrą tašką K, tada tiesę KK 1 jų sankirta eina per tašką K ir yra lygiagreti briaunai BB 1 . Pažymime šios tiesės susikirtimo tašką su tiese QM: K 1 = KK 1 ∩ QM, KK 1 ║ BB 1 . Kadangi QM є α, tada K 1 є α.

Ryžiai. 10

Gauta: Р є α, K 1 є α => tiesus RK 1 є α, o RK 1 ∩ AA 1 = R. Taškas R yra plokštumos α ir briaunos AA susikirtimo taškas 1 (R = α ∩ AA 1 ), todėl yra norimos sekcijos viršūnė. Panašiai sukonstruojame tašką N = α ∩ СС 1 .

Taigi norimos sekcijos „žingsnių“ seka yra tokia:

K = AD ∩ BE; 2. K 1 = KK 1 ∩ MQ, KK 1 || BB 1;

R = RK 1 ∩ AA 1 ; 4. H = EC ∩AD;

H 1 – HH 1 ∩ РR, НН 1 || CC 1; 6.N = QН 1 ∩ СС 1.

Pentagon MNPQR yra reikalinga sekcija.

Šioje pamokoje apžvelgsime tetraedrą ir jo elementus (tetraedro kraštą, paviršių, paviršius, viršūnes). Ir mes išspręsime keletą problemų, susijusių su tetraedro atkarpų konstravimu bendras metodas sekcijoms statyti.

Tema: Tiesių ir plokštumų lygiagretumas

Pamoka: Tetraedras. Tetraedro atkarpų konstravimo uždaviniai

Kaip sukurti tetraedrą? Paimkime savavališką trikampį ABC. Bet koks taškas D, esantis ne šio trikampio plokštumoje. Gauname 4 trikampius. Šių 4 trikampių suformuotas paviršius vadinamas tetraedru (1 pav.). Vidiniai taškai, apriboti šio paviršiaus, taip pat yra tetraedro dalis.

Ryžiai. 1. Tetraedras ABCD

Tetraedro elementai
A,B, C, D - tetraedro viršūnės.
AB, A.C., REKLAMA, B.C., BD, CD - tetraedro briaunos.
ABC, ABD, BDC, ADC - tetraedro veidai.

komentaras: galima paimti butu ABC už nugaros tetraedro bazė, o tada nurodykite D yra tetraedro viršūnė. Kiekviena tetraedro briauna yra dviejų plokštumų sankirta. Pavyzdžiui, šonkaulis AB- tai plokštumų sankirta ABD Ir ABC. Kiekviena tetraedro viršūnė yra trijų plokštumų sankirta. Viršūnė A guli plokštumose ABC, ABD, ADSU. Taškas A yra trijų nurodytų plokštumų sankirta. Šis faktas parašytas taip: A= ABC ∩ ABD ∩ ACD.

Tetraedro apibrėžimas

Taigi, tetraedras yra paviršius, sudarytas iš keturių trikampių.

Tetraedro kraštas- dviejų tetraedro plokštumų susikirtimo linija.

Iš 6 degtukų padarykite 4 vienodus trikampius. Lėktuve problemos išspręsti neįmanoma. Ir tai lengva padaryti erdvėje. Paimkime tetraedrą. 6 degtukai yra jo kraštai, keturi tetraedro paviršiai ir bus keturi vienodi trikampiai. Problema išspręsta.

Duotas tetraedras ABCD. Taškas M priklauso tetraedro kraštui AB, taškas N priklauso tetraedro kraštui IND ir laikotarpis R priklauso kraštui DSU(2 pav.). Sukurkite tetraedro atkarpą su plokštuma MNP.

Ryžiai. 2. 2 uždavinio brėžinys – Sukonstruokite tetraedro pjūvį su plokštuma

Sprendimas:
Apsvarstykite tetraedro veidą DSaulė. Šiuo klausimu N Ir P priklauso veidams DSaulė, taigi ir tetraedras. Bet pagal punkto būklę N, P priklauso pjovimo plokštumai. Reiškia, NP- tai dviejų plokštumų susikirtimo linija: veido plokštuma DSaulė ir pjovimo plokštuma. Tarkime, kad tiesios linijos NP Ir Saulė ne lygiagrečiai. Jie guli toje pačioje plokštumoje DSaulė. Raskime tiesių susikirtimo tašką NP Ir Saulė. Pažymėkime tai E(3. pav.).

Ryžiai. 3. 2 uždavinio brėžinys. E taško radimas

Taškas E priklauso pjūvio plokštumai MNP, nes jis yra ant linijos NP, ir tiesi linija NP yra visiškai pjūvio plokštumoje MNP.

Taip pat taškas E guli plokštumoje ABC, nes jis yra tiesioje linijoje Saulė iš lėktuvo ABC.

Mes tai gauname VALGYTI- plokštumų susikirtimo linija ABC Ir MNP, nuo taškų E Ir M gulėti vienu metu dviejose plokštumose - ABC Ir MNP. Sujunkime taškus M Ir E, ir tęskite tiesiai VALGYTI iki sankryžos su linija AC. Linijų susikirtimo taškas VALGYTI Ir AC pažymėkime K.

Taigi šiuo atveju NPQМ- reikiamą skyrių.

Ryžiai. 4. 2 uždavinio brėžinys. 2 uždavinio sprendimas

Dabar panagrinėkime atvejį, kai NP lygiagrečiai B.C.. Jei tiesiai NP lygiagrečiai kokiai nors linijai, pavyzdžiui, tiesei Saulė iš lėktuvo ABC, tada tiesiai NP lygiagrečiai visai plokštumai ABC.

Norima pjūvio plokštuma eina per tiesią liniją NP, lygiagrečiai plokštumai ABC, ir kerta plokštumą tiesia linija MQ. Taigi susikirtimo linija MQ lygiagrečiai linijai NP. Mes gauname NPQМ- reikiamą skyrių.

Taškas M guli ant šono ADIN tetraedras ABCD. Sukurkite tetraedro atkarpą su plokštuma, kuri eina per tašką M lygiagrečiai pagrindui ABC.

Ryžiai. 5. 3 uždavinio brėžinys Sukonstruokite tetraedro pjūvį su plokštuma

Sprendimas:
Pjovimo plokštuma φ lygiagrečiai plokštumai ABC pagal sąlygą tai reiškia, kad šis lėktuvas φ lygiagrečiai linijoms AB, AC, Saulė.
Lėktuve ABD per tašką M padarykime tiesioginį PQ lygiagrečiai AB(5 pav.). Tiesiai PQ guli plokštumoje ABD. Panašiai ir lėktuve ACD per tašką R padarykime tiesioginį PR lygiagrečiai AC. Gavau tašką R. Dvi susikertančios linijos PQ Ir PR lėktuvas PQR atitinkamai lygiagrečios dviem susikertančioms tiesėms AB Ir AC lėktuvas ABC, o tai reiškia lėktuvus ABC Ir PQR lygiagrečiai. PQR- reikiamą skyrių. Problema išspręsta.

Duotas tetraedras ABCD. Taškas M- vidinis taškas, taškas tetraedro paviršiuje ABD. N- vidinis segmento taškas DSU(6. pav.). Sukurkite tiesės susikirtimo tašką N.M. ir lėktuvai ABC.

Ryžiai. 6. 4 uždavinio brėžinys

Sprendimas:
Norėdami tai išspręsti, sukonstruosime pagalbinę plokštumą DMN. Tegul būna tiesiai DM taške kerta tiesę AB KAM(7. pav.). Tada SKD– tai lėktuvo atkarpa DMN ir tetraedras. Lėktuve DMN meluoja ir tiesiai N.M., ir gautą tiesią liniją SK. Taigi, jei N.M. ne lygiagrečiai SK, tada jie tam tikru momentu susikirs R. Taškas R ir bus norimas linijos susikirtimo taškas N.M. ir lėktuvai ABC.

Ryžiai. 7. 4 uždavinio brėžinys. 4 uždavinio sprendimas

Duotas tetraedras ABCD. M- vidinis veido taškas ABD. R- vidinis veido taškas ABC. N- vidinis krašto taškas DSU(8 pav.). Sukurkite tetraedro atkarpą su plokštuma, einančia per taškus M, N Ir R.

Ryžiai. 8. 5 uždavinio brėžinys Sukonstruokite tetraedro pjūvį su plokštuma

Sprendimas:
Panagrinėkime pirmąjį atvejį, kai tiesi linija MN ne lygiagreti plokštumai ABC. Ankstesniame uždavinyje radome linijos susikirtimo tašką MN ir lėktuvai ABC. Tai yra esmė KAM, jis gaunamas naudojant pagalbinę plokštumą DMN, t.y. Mes darome DM ir gauname tašką F. Vykdome CF ir sankryžoje MN gauname tašką KAM.

Ryžiai. 9. Uždavinio brėžinys 5. Taško K radimas

Padarykime tiesioginį KR. Tiesiai KR guli ir pjūvio plokštumoje, ir plokštumoje ABC. Gauti taškus P 1 Ir R 2. Prisijungimas P 1 Ir M ir kaip tęsinį gauname esmę M 1. Taško sujungimas R 2 Ir N. Dėl to gauname norimą skyrių Р 1 Р 2 NM 1. Pirmuoju atveju problema išspręsta.
Panagrinėkime antrąjį atvejį, kai tiesi linija MN lygiagrečiai plokštumai ABC. Lėktuvas MNP eina per tiesią liniją MN lygiagrečiai plokštumai ABC ir kerta plokštumą ABC palei kažkokią tiesią liniją R 1 R 2, tada tiesiai R 1 R 2 lygiagrečiai nurodytai linijai MN(10 pav.).

Ryžiai. 10. Uždavinio brėžinys 5. Reikalingas skyrius

Dabar nubrėžkime tiesią liniją R 1 M ir gauname tašką M 1.Р 1 Р 2 NM 1- reikiamą skyrių.

Taigi, pažvelgėme į tetraedrą, kai kuriuos išsprendėme tipinės užduotysį tetraedrą. Kitoje pamokoje pažvelgsime į gretasienį.

1. I. M. Smirnova, V. A. Smirnovas. - 5-asis leidimas, taisytas ir papildytas - M.: Mnemosyne, 2008. - 288 p. : nesveikas. Geometrija. 10-11 klasės: vadovėlis mokiniams švietimo įstaigų(pagrindinis ir profilio lygiai)

2. Šaryginas I.F. – M.: Bustardas, 1999. – 208 p.: iliustr. Geometrija. 10-11 klasės: Vadovėlis bendrojo ugdymo įstaigoms

3. E. V. Potoskujevas, L. I. Zvalichas. - 6-asis leidimas, stereotipas. - M.: Bustard, 008. - 233 p. :il. Geometrija. 10 klasė: Vadovėlis bendrojo ugdymo įstaigoms su giluminiu ir specializuotu matematikos mokymu

Papildomi žiniatinklio ištekliai

2. Kaip sukonstruoti tetraedro skerspjūvį. Matematika ().

3. Festivalis pedagoginės idėjos ().

Atlikite užduotis namuose tema „Tetraedras“, kaip rasti tetraedro kraštą, tetraedro paviršius, tetraedro viršūnes ir paviršių

1. Geometrija. 10-11 klasės: vadovėlis bendrojo ugdymo įstaigų mokiniams (pagrindinio ir specializuoto lygio) I. M. Smirnova, V. A. Smirnov. - 5-asis leidimas, taisytas ir papildytas - M.: Mnemosyne, 2008. - 288 p.: iliustr. 18, 19, 20 užduotys 50 psl

2. Taškas E vidurio šonkaulis MA tetraedras MAVS. Sukurkite tetraedro atkarpą su plokštuma, einančia per taškus B, C Ir E.

3. Tetraedro MABC taškas M priklauso paviršiui AMV, taškas P priklauso veidui BMC, taškas K priklauso briaunai AC. Sukurkite tetraedro atkarpą su plokštuma, einančia per taškus M, R, K.

4. Kokias figūras galima gauti susikirtus tetraedrui su plokštuma?

Darbo tikslas:
Erdvinių sampratų kūrimas.
Užduotys:
1. Supažindinti su ruožų statybos taisyklėmis.
2. Ugdykite atkarpų konstravimo įgūdžius
tetraedras ir gretasienis skiriasi
pjovimo plokštumos nurodymo atvejai.
3. Ugdykite gebėjimą taikyti taisykles
statant skyrius sprendžiant problemas
temos „Poliedrai“.

Norėdami išspręsti daugelį
geometrinis
reikalingos užduotys
statyti sekcijas
daugiakampis
įvairių
lėktuvai.

Pjovimo plokštumos samprata

Sekantas
lėktuvas
gretasienis
(tetraedras)
vadinamas bet kuriuo
plokštuma, iš abiejų pusių
pusės nuo
kuris turi
duotųjų taškų
gretasienis
(tetraedras).

Daugiakampio atkarpos samprata

Pjovimo plokštuma
kerta kraštus
tetraedras
(lygiagretainis) pagal
segmentai.
Daugiakampis, šonai
kurie duomenys yra
segmentai vadinami
tetraedro skerspjūvis
(lygiagretainis).

Darbas pagal brėžinius

Kiek plokštumų galima nupiešti
per pasirinktus elementus?
Kokias aksiomas ir teoremas taikėte?

Norėdami sukurti skyrių
reikia braižyti taškus
sekantinė sankryža
plokštumos su briaunomis ir
sujungti juos segmentais.

Atkarpų konstravimo taisyklės

1. Galite sujungti tik du
taškai, esantys vieno plokštumoje
briaunos.
2. Pjovimo plokštuma susikerta
lygiagrečiai išilgai
lygiagrečiai segmentai.

Atkarpų konstravimo taisyklės

3. Jei veido plokštuma pažymėta
priklauso tik vienas taškas
pjūvio plokštuma, tada tai būtina
pastatyti papildomą tašką.
Norėdami tai padaryti, turite rasti taškus
jau pastatytų sankryžų
tiesios linijos su kitomis tiesiomis linijomis,
guli ant tų pačių kraštų.

10. Tetraedrų pjūvių konstravimas

11.

Tetraedras turi 4 veidus
Skyriuose gali pasirodyti
Trikampiai
Keturkampiai

12.

Sukurkite tetraedro skerspjūvį
DABC lėktuvas pravažiuoja
per taškus M,N,K
1. Nubrėžkime tiesią liniją
taškais M ir K, nes jie meluoja
viename veide (ADC).
D
M
A.A.
N
K
BB
CC
2. Nubrėžkime tiesią liniją
taškais K ir N, nes Jie
gulėti toje pačioje pusėje
(CDB).
3. Ginčiuodami panašiai,
nubrėžkite tiesią liniją MN.
4. Trikampis MNK –
norimą skyrių.

13. einantis per tašką M lygiagrečiai ABC.

D
1. Brėžkime per tašką M
tiesi lygiagreti
briauna AB
2.
M
R
A
KAM
SU
IN
Pereikime per tašką M
tiesi lygiagreti
kraštas AC
3. Nubrėžkime tiesią liniją
taškais K ir P, nes jie guli
vienas veidas (DBC)
4. Trikampis MPK –
norimą skyrių.

14.

Sukurkite tetraedro atkarpą plokštuma,
eina per taškus E, F, K.
D
1. Atliekame KF.
2. Atliekame FE.
3. Tęskime
EF, tęskime AC.
F
4.EF AC =M
5. Vykdome
MK.
E
M
AB = L
6.
MK
C
A
7. Elgesys EL
L
EFKL – reikalingas skyrius
K
B

15.

Sukurkite tetraedro atkarpą plokštuma,
eina per taškus E, F, K
Kurie
kas tiesiai
taškas,
gulėdamas
Gali
Prisijungti
gautas
Kuris
taškų
Gali
iškarto
kad
arba
briaunos
Gali
Tęsti,
į
gauti
taškai,
meluoja
V
vienas
Prisijungti?
Prisijungti
gavo
papildomas
taškas?
kraštai,
vardas
skyrius.
papildomas taškas?
D
AC
ELFK
FSEC
ir taškas
K ir E
ir FK
F
L
C
M
A
E
K
B

16.

Sukurkite sekciją
tetraedro plokštuma,
einantis per taškus
E, F, K.
D
F
L
C
A
E
K
B
APIE

17.

Išvada: nesvarbu, koks metodas
statybos skyriai yra vienodi

18. Lygiagretainių atkarpų konstravimas

19.

Tetraedras turi 6 veidus
Trikampiai
Pentagonai
Jos skyriuose gali pasirodyti
Keturkampiai
Šešiakampiai

20. Sukurkite gretasienio atkarpą su plokštuma, einančia per tašką X, lygiagrečią plokštumai (OSV)

1
A1
Y
X
D1
S
IN
A
D
Z
1. Pakalbėkime apie tai
C1
taškas X tiesi linija
lygiagrečiai kraštui
D1C1
2. Per tašką X
tiesioginis
lygiagrečiai kraštui
D1D
3. Per tašką Z yra tiesi linija
lygiagrečiai kraštui
SU
DC
4. Nubrėžkime tiesią liniją
taškai S ir Y, nes jie guli
vienas veidas (BB1C1)
XYSZ – reikalingas skyrius

21.

Sukurkite gretasienio atkarpą
plokštuma, einanti per taškus
PIKTAS
1
D1
E
A1
C1
IN
A
1. Kr
2. MD
3. AŠ//AD, nes (ABC)//(A1B1C1)
4. A.E.
5. AEMD – reikalingas skyrius
M
D
SU

22. Sukurkite gretasienio pjūvį su plokštuma, einančia per taškus M, K, T

N
M
KAM
R
S
X
T

23. Užduotis atlikite patys

m
T
Į
m
D
Į
T
Sukonstruoti pjūvį iš: a) gretasienio;
b) tetraedras
plokštuma, kertanti taškus M, T, K.

24. Naudoti ištekliai

Soboleva L. I. Sekcijos statyba
Tkacheva V.V. Sekcijos statyba
tetraedras ir gretasienis
Gobozova L.V. Statybos problemos
skyriuose
DVD. Geometrijos pamokos iš Kirilo ir
Metodijus. 10 klasė, 2005 m
Mokymo ir testavimo užduotys.
Geometrija. 10 klasė (Užrašų knygelė)/Alešina
T.N. – M.: Intelekto centras, 1998 m

Planimetrijos aksiomos:

Skirtinguose vadovėliuose tiesių ir plokštumų savybės gali būti pateikiamos įvairiai – aksiomos, jos išvados, teoremos, lemos ir kt. Apsvarstykite Pogorelovo A.V. vadovėlį.

Tiesi linija padalija plokštumą į dvi pusplokštumas.

Iš bet kurios pusės tiesės galima nubrėžti kampą su tam tikra pusplokštuma į nurodytą pusplokštumą. laipsnio matas, mažiau nei 180 0 , ir tik vienas.

Kad ir koks būtų trikampis, tam tikroje vietoje yra lygus trikampis tam tikros pustiesės atžvilgiu.

Per tašką, esantį ne ant duotosios tiesės, plokštumoje galima nubrėžti daugiausia vieną tiesę, lygiagrečią duotajai.

Stereometrijos aksiomos:

Kad ir kokia būtų plokštuma, yra taškų, kurie priklauso šiai plokštumai, ir taškų, kurie nepriklauso šiai plokštumai, ir taškų, kurie jai nepriklauso.

Jei dvi skirtingos plokštumos turi bendrą tašką, tada jos susikerta išilgai tiesės, einančios per šį tašką.

Jei dvi skirtingos linijos turi bendrą tašką, tada per jas galima nubrėžti plokštumą ir tik vieną.

Kad ir kokia būtų linija, yra taškų, kurie priklauso šiai linijai, ir taškų, kurie jai nepriklauso.

Per bet kuriuos du taškus galite nubrėžti tiesią liniją ir tik vieną.

Iš trijų linijos taškų vienas ir tik vienas yra tarp kitų dviejų.

Kiekvienas segmentas turi tam tikrą ilgį, didesnį už nulį. Atkarpos ilgis lygus dalių, į kurias jis padalintas iš bet kurio iš jos taškų, ilgių sumai.

Plokštumai priklausanti tiesė padalija šią plokštumą į dvi pusplokštumas.

Kiekvienas kampas turi tam tikrą laipsnio matą, didesnį už nulį. Tiesus kampas yra 180 0 . Kampo laipsnio matas yra lygus kampų, į kuriuos jis yra padalintas iš bet kurio spindulio, einančio tarp jo kraštų, laipsnio matų sumai.

Bet kurioje pustiesėje nuo pradinio taško galite nubrėžti tam tikro ilgio atkarpą ir tik vieną.

Iš pusės tiesės plokštumoje, kurioje jis yra, kampą, kurio tam tikro laipsnio matas yra mažesnis nei 180, galima nubraižyti į nurodytą pusplokštumą 0 , ir tik vienas.

Kad ir koks būtų trikampis, tam tikroje plokštumoje tam tikroje vietoje yra lygus trikampis, palyginti su duota tos plokštumos pustiese.

Plokštumoje per duotą tašką, kuris nėra tam tikroje tiesėje, galima nubrėžti daugiausia vieną tiesę, lygiagrečią duotajai.

Skyrius

Erdvėje dvi figūros, mūsų atveju plokštuma ir daugiakampis, gali turėti tokį tarpusavio išsidėstymą: nesikerta, susikerta taške, susikerta tiesia linija ir plokštuma kerta daugiakampį išilgai jo vidaus (1 pav.) , ir tuo pačiu metu suformuokite šiuos skaičius:

a) tuščia figūra (nesikerta)

b) taškas

c) segmentas

d) daugiakampis

Jei daugiakampio ir plokštumos sankirtoje yra daugiakampis, tai šis daugiakampisvadinama daugiakampio atkarpa su plokštuma .

1 pav

Apibrėžimas. Skyrius erdvinis kūnas (pavyzdžiui, daugiakampis) yra figūra, atsirandanti kūno susikirtimo su plokštuma.

Pjovimo plokštuma daugiakampis vadinkime bet kurią plokštumą, kurios abiejose pusėse yra tam tikro daugiakampio taškai.

Nagrinėsime tik atvejį, kai plokštuma kerta daugiakampį išilgai jo vidaus. Šiuo atveju šios plokštumos sankirta su kiekvienu daugiakampio paviršiumi bus tam tikra atkarpa.

Jei plokštumos susikerta tiesia linija, tai vadinama tiesesekdami vieną iš šių plokštumų į kitą.

Apskritai daugiakampio pjovimo plokštuma kertasi su kiekvieno jo paviršiaus plokštuma (taip pat ir su bet kuria kita šio daugiakampio pjovimo plokštuma). Jis taip pat kerta kiekvieną tiesę, ant kurios yra daugiakampio briaunos.

Tiesi linija, išilgai kurios pjovimo plokštuma kerta bet kurio daugiakampio paviršiaus plokštumą, vadinamasekdami pjovimo plokštumą šio paviršiaus plokštumoje, o taškas, kuriame pjovimo plokštuma kerta tiesę, kurioje yra bet kuris daugiakampio kraštas, vadinamassekdami pjovimo plokštumą įjungtaši tiesi linija. Šis taškas taip pat yra linijos pėdsakas pjovimo plokštumoje. Jei pjovimo plokštuma tiesiogiai kerta daugiakampio paviršių, tada galime kalbėti apie pjovimo plokštumos pėdsaką ant veido ir, panašiai, apiepjovimo plokštumos pėdsakas daugiakampio krašte, tai yra apie briaunos pėdsaką pjovimo plokštumoje.

Kadangi tiesią liniją vienareikšmiškai nustato du taškai, norint rasti pjovimo plokštumos pėdsaką bet kurioje kitoje plokštumoje ir ypač bet kurio daugiakampio paviršiaus plokštumoje, pakanka sudaryti du bendrus plokštumų taškus.

Norint sukonstruoti pjovimo plokštumos pėdsaką, taip pat su šia plokštuma sukonstruoti daugiakampio atkarpą, reikia nurodyti ne tik daugiakampį, bet ir pjovimo plokštumą. O pjūvio plokštumos konstrukcija priklauso nuo šios plokštumos specifikacijos. Pagrindiniai plokštumos, ypač pjovimo plokštumos, apibrėžimo būdai yra šie:

trys taškai, esantys ne vienoje tiesėje;

tiesi linija ir ne ant jos esantis taškas;

dvi lygiagrečios linijos;

dvi susikertančios linijos;

taškas ir dvi susikertančios tiesės;

Galimi ir kiti pjovimo plokštumos nurodymo būdai.

Todėl visus daugiakampių atkarpų konstravimo būdus galima suskirstyti į metodus.

Daugiakampių pjūvių konstravimo metodai

Daugiakampių pjūvių metodas stereometrijoje naudojamas statybos uždaviniuose. Jis pagrįstas gebėjimu sukurti daugiakampio atkarpą ir nustatyti atkarpos tipą.

Yra trys pagrindiniai daugiakampio atkarpų konstravimo būdai:

Aksiominis metodas:

Atsekimo metodas.

Kombinuotas metodas.

Koordinatės metodas.

Pastaba kad pėdsakų metodas ir pagalbinio skyriaus metodas yra atmainosAksiominis atkarpų konstravimo metodas.

Taip pat galime išskirti šiuos daugiakampių pjūvių konstravimo būdus:

daugiabriaunio atkarpos su plokštuma, einančia per tam tikrą tašką, lygiagrečiai duotajai plokštumai, sudarymas;

atkarpos, einančios per tam tikrą tiesę, lygiagrečią kitai duotai linijai, sukūrimas;

per duotą tašką lygiagrečios dviem duotoms susikertančioms tiesėms atkarpos sukūrimas;

daugiabriaunio atkarpos su plokštuma, einančia per duotąją tiesę, statmeną duotai plokštumai, sudarymas;

statant daugiabriaunio atkarpą su plokštuma, einančia per tam tikrą tašką statmenai nurodytai tiesei.

Pagrindiniai veiksmai, sudarantys atkarpų konstravimo metodus, yra tiesės susikirtimo su plokštuma taško radimas, dviejų plokštumų susikirtimo linijos sukūrimas, tiesės, lygiagrečios plokštumai, statmenos plokštumai sukūrimas. Norint sukurti dviejų plokštumų susikirtimo liniją, dažniausiai surandami du jos taškai ir per juos nubrėžiama linija. Norėdami sukurti tiesės ir plokštumos susikirtimo tašką, plokštumoje raskite tiesę, kuri kerta duotąją. Tada rastos linijos sankirtoje su duotuoju gaunamas norimas taškas.

Panagrinėkime atskirai tuos, kuriuos išvardijomeDaugiakampių atkarpų konstravimo būdai:

Atsekimo metodas.

Atsekimo metodas yra pagrįstas (remiantis) stereometrijos aksiomomis, metodo esmė – sukonstruoti pagalbinę liniją, kuri yra pjovimo plokštumos susikirtimo su bet kurio figūros paviršiaus plokštuma linijos vaizdas. Patogiausia konstruoti pjovimo plokštumos susikirtimo linijos su apatinio pagrindo plokštuma vaizdą. Ši linijavadinamas pagrindiniu pjovimo plokštumos pėdsaku . Naudojant pėdsaką, lengva sukurti pjovimo plokštumos taškų, esančių figūros šoniniuose kraštuose arba paviršiuose, vaizdus. Nuosekliai sujungdami šių taškų vaizdus, gauname norimos sekcijos vaizdą.

Prisimink tai kad statant pagrindinį pjovimo plokštumos pėdsaką naudojamas toks teiginys.

Jei taškai priklauso pjovimo plokštumai ir nėra toje pačioje tiesėje, o jų projekcija (centrinė arba lygiagreti) į plokštumą, pasirinktą kaip pagrindinė, taškai yra atitinkamai tada atitinkamų tiesių susikirtimo taškai, tai yra taškai ir yra toje pačioje tiesėje (1 pav., a, b).

1.a pav.1.b pav

Ši tiesi linija yra pagrindinis pjovimo plokštumos pėdsakas. Kadangi taškai yra ant pagrindinio pėdsako, jį sukonstruoti pakanka rasti du taškus iš šių trijų.

Pagalbinių sekcijų metodas.

Šis daugiakampių atkarpų konstravimo būdas yra gana universalus. Tais atvejais, kai norimas pjovimo plokštumos pėdsakas (arba pėdsakai) yra už brėžinio ribų, šis būdas netgi turi tam tikrų privalumų. Tuo pačiu metu reikia nepamiršti, kad šiuo metodu atliekamos konstrukcijos dažnai būna „perkrautos“. Tačiau kai kuriais atvejais pagalbinių sekcijų metodas yra racionaliausias.

Kombinuotas metodas

Kombinuoto daugiakampio atkarpų konstravimo metodo esmė yra teoremų apie tiesių ir plokštumų lygiagretumą erdvėje taikymas kartu su aksiomatiniu metodu.

Atkarpų konstravimo koordinačių metodas.

Koordinačių metodo esmė – skaičiuoti briaunų arba daugiakampio susikirtimo taškų koordinates su pjovimo plokštuma, kurią nurodo plokštumos lygtis. Pjovimo plokštumos lygtis apskaičiuojama pagal problemos sąlygas.

Pastaba , kad šis daugiakampio atkarpos konstravimo būdas yra priimtinas kompiuteriui, nes jis susijęs su dideliu skaičiavimų kiekiu, todėl šį metodą patartina įgyvendinti kompiuteriu.

Mūsų pagrindinė užduotis bus sukonstruoti daugiakampio atkarpą su plokštuma, t.y. statant šių dviejų aibių sankirtą.

Daugiakampių pjūvių statyba

Pirmiausia atkreipiame dėmesį, kad išgaubto daugiakampio atkarpa yra išgaubtas plokščias daugiakampis, kurio viršūnės bendruoju atveju yra pjovimo plokštumos susikirtimo taškai su daugiakampio kraštinėmis, o kraštinės – su jo kraštinėmis. veidai.

Sekcijos konstravimo pavyzdžiai:

Sekcijos apibrėžimo metodai yra labai įvairūs. Dažniausias iš jų yra pjovimo plokštumos nustatymas trimis taškais, kurie nėra toje pačioje tiesėje.

1 pavyzdys. Skirta gretasieniui ABCDA 1 B 1 C 1 D 1 . Sukurkite atkarpą, einančią per taškus M, N, L.

Sprendimas:

Sujunkite taškus M ir L, esančius plokštumoje AA 1 D 1 D.

Sukirskime tiesę ML (priklausančią atkarpai) su briauna A 1 D 1 1 D 1 D. Gaukite tašką X 1 .

Taškas X1 yra A krašte 1 D 1 , taigi ir lėktuvas A 1 B 1 C 1 D 1 , sujungiame jį N dygsniu, esančiu toje pačioje plokštumoje.

X 1 N kerta kraštą A 1 B 1 taške K.

Sujunkite taškus K ir M, esančius toje pačioje plokštumoje AA 1 B 1 B.

Raskime pjūvio plokštumos susikirtimo tiesę su DD plokštuma 1 C 1 C:

Sukirsime tiesę ML (priklausančią atkarpai) su briauna DD 1 , jie guli toje pačioje plokštumoje AA 1 D 1 D, gauname tašką X 2 .

Sukirsime tiesę KN (priklausančią atkarpai) su briauna D 1 C 1 , jie guli toje pačioje plokštumoje A 1 B 1 C 1 D 1 , gauname tašką X3;

Taškai X2 ir X3 yra DD plokštumoje 1 C 1 C. Nubrėžkite tiesę X 2 X 3 , kuris kerta kraštą C 1 C taške T, o briauna DC taške P. Ir sujunkite taškus L ir P, esančius plokštumoje ABCD.

Taigi, problema laikoma išspręsta, jei randami visi segmentai, išilgai kurių plokštuma kerta daugiakampio paviršius, ką mes padarėme. MKNTPL – reikalingas skyrius.

Pastaba. Tą pačią atkarpos konstravimo problemą galima išspręsti naudojant lygiagrečių plokštumų savybę.

Iš to, kas išdėstyta aukščiau, galite sukurti algoritmą (taisyklę), skirtą tokio tipo problemoms spręsti.

Daugiakampių pjūvių konstravimo taisyklės:

2 pavyzdys. DL, M

Išspręskime aksiomatiniu metodu:

Nubraižykime pagalbinę plokštumąDKM, kuri kerta kraštines AB ir BC taškuose E irF(sprendimo eiga 2 pav.). Šioje pagalbinėje plokštumoje sukonstruokime pjūvio plokštumos CM „pėdsaką“, raskime CM ir E susikirtimo taškąF– taškas P. Taškas P, kaipL, yra ABC plokštumoje, ir galima nubrėžti tiesią liniją, išilgai kurios pjūvio plokštuma kerta ABC plokštumą („pjūvio pėdsakas“ ABC plokštumoje).

3 pavyzdys. MABCD piramidės kraštinėse AB ir AD atitinkamai apibrėžiame taškus P ir Q, šių briaunų vidurio taškus, o briaunoje MC – tašką R. Sukonstruosime piramidės atkarpą su plokštuma, einančia per taškais P, Q ir R.

Sprendimą atliksime kombinuotu metodu:

1). Aišku, kad pagrindinis plokštumos PQR pėdsakas yra tiesė PQ.

2). Raskime tašką K, kuriame MAC plokštuma kerta tiesę PQ. Taškai K ir R priklauso ir PQR plokštumai, ir MAC plokštumai. Todėl nubrėžę tiesę KR, gauname šių plokštumų susikirtimo liniją.

3). Raskime tašką N=AC BD, nubrėžkime tiesę MN ir raskime tašką F=KR MN.

4). Taškas F yra bendras plokštumų PQR ir MDB taškas, tai yra, šios plokštumos susikerta išilgai tiesės, einančios per tašką F. Tačiau kadangi PQ - vidurinė linija trikampis ABD, tada PQ lygiagreti BD, tai yra, tiesė PQ lygiagreti plokštumai MDB. Tada plokštuma PQR, einanti per tiesę PQ, kerta plokštumą MDB išilgai tiesės, lygiagrečios tiesei PQ, ty lygiagrečia ir tiesia BD. Todėl plokštumoje MDB per tašką F brėžiame tiesę, lygiagrečią tiesei BD.

5). Tolesnės konstrukcijos aiškiai matomos paveikslėlyje. Dėl to gauname daugiakampį PQD"RB" - norimą atkarpą

Panagrinėkime prizmės skerspjūvius dėl paprastumo, tai yra loginio mąstymo patogumo, panagrinėkime kubo dalis (3.a pav.):

Ryžiai. 3.a

Prizmės pjūviai, kurių plokštumos lygiagrečios šoninėms briaunoms, yra lygiagretainiai. Visų pirma, įstrižainės yra lygiagretainiai (4 pav.).

Def. Įstrižainė pjūvis Prizmė pjaunama plokštuma, einanti per du šoninius kraštus, kurie nepriklauso tam pačiam paviršiui.

Daugiakampis, gaunamas iš prizmės įstrižainės pjūvio, yra lygiagretainis. Klausimas apie įstrižainių sekcijų skaičiųn-kampinė prizmė yra sunkesnė nei įstrižainių skaičiaus klausimas. Atkarpų bus tiek, kiek yra įstrižainių prie pagrindo. Mes žinome, kad išgaubtos prizmės pagrinduose yra išgaubti daugiakampiai, o išgaubta prizmėn- įstrižainių kampas. Taigi galime sakyti, kad įstrižainių pjūvių yra perpus mažiau nei įstrižainių.

Pastaba: Paveiksle statant gretasienio atkarpas, reikia atsižvelgti į tai, kad jei pjovimo plokštuma išilgai kai kurių atkarpų kerta du priešingus paviršius, tai šios atkarpos yra lygiagrečios „gretasienio savybe, t.y. Priešingi gretasienio paviršiai yra lygiagretūs ir lygūs.

Pateiksime atsakymus į dažniausiai užduodamus klausimus:

Kokie daugiakampiai gaunami, kai kubas perpjaunamas plokštuma?

"trikampis, keturkampis, penkiakampis, šešiakampis".

Ar kubą galima lėktuvu perpjauti į septyniakampį? O aštuonkampis?

"negaliu".

3) Kyla klausimas: koks yra didžiausias daugiakampio kraštinių skaičius, gaunamas perpjaunant daugiakampį plokštuma?

Didžiausias daugiakampio kraštinių skaičius, gautas perpjaunant daugiakampį plokštuma, yra lygus daugiakampio paviršių skaičiui .

3 pavyzdys. Sukurkite prizmės A skerspjūvį 1 B 1 C 1 D 1 ABCD plokštuma, kertanti tris taškus M, N, K.

Panagrinėkime taškų M, N, K išsidėstymo prizmės paviršiuje atvejį (5 pav.).

Apsvarstykite atvejį: B tokiu atveju akivaizdu, kad M1 = B1.

Konstrukcija:

4 pavyzdys. Sukurkite gretasienio ABCDA atkarpą 1 B 1 C 1 D 1 plokštuma, einanti per taškus M, N, P (taškai nurodyti brėžinyje (6 pav.)).

Sprendimas:

Ryžiai. 6

Taškai N ir P yra pjūvio plokštumoje ir gretasienio apatinio pagrindo plokštumoje. Sukurkime tiesią liniją, einančią per šiuos taškus. Ši tiesi linija yra pjovimo plokštumos pėdsakas į gretasienio pagrindo plokštumą.

Tęskime tiesę, kurioje yra gretasienio AB pusė. Tiesės AB ir NP susikerta tam tikru tašku S. Šis taškas priklauso pjūvio plokštumai.

Kadangi taškas M taip pat priklauso pjūvio plokštumai ir kerta tiesę AA 1 tam tikru momentu X.

Taškai X ir N yra toje pačioje paviršiaus AA plokštumoje 1 D 1 D, sujunkite juos ir gaukite tiesią liniją XN.

Kadangi gretasienio paviršių plokštumos yra lygiagrečios, tai per tašką M galime nubrėžti tiesią liniją į veidą A 1 B 1 C 1 D 1 , lygiagrečiai tiesei NP. Ši linija susikirs su B puse 1 SU 1 taške Y.

Panašiai nubrėžiame tiesę YZ, lygiagrečią tiesei XN. Sujungiame Z su P ir gauname norimą skyrių - MYZPNX.

Piramidės pjūviai plokštumų, einančių per jos viršūnę, yra trikampiai. Visų pirma, trikampiai yra įstrižainės. Tai atkarpos plokštumų, einančių per du negretimus šoninius piramidės kraštus.

4 pavyzdys. Sukonstruoti piramidės ABC atkarpąDplokštuma, einanti per taškus K,L, M.

Sprendimas:

Išspręskime tą patį pavyzdį kitaip .

Tarkime, kad taškuose K,L, ir M sukonstruota sekcijaKLNM(7 pav.). Pažymėkime pagalFketurkampio įstrižainių susikirtimo taškasKLNM. Padarykime tiesioginįDFir žymėtiF 1 jo susikirtimo taškas su briauna ABC. TaškasF 1 sutampa su tiesių AM ir SC susikirtimo tašku (F 1 kartu priklauso AM plokštumomsDIrDSK). Pilnas sustojimasF 1 lengva statyti. Toliau statome taškąFkaip susikirtimo taškasDF 1 IrL.M.. Toliau randame taškąN.

Nagrinėjama technika vadinamavidaus projektavimo metodas . (Mūsų atveju mes kalbame apie apie centrinį dizainą. KeturkampisKMSA yra keturkampio projekcijaKMNLnuo taškoD. Šiuo atveju įstrižainių susikirtimo taškasKMNL- taškasF– eina į keturkampio įstrižainių susikirtimo taškąKMSA – taškasF 1 .

Daugiakampio pjūvio plotas.

Daugiakampio skerspjūvio ploto apskaičiavimo problema paprastai sprendžiama keliais etapais. Jei uždavinyje nurodoma, kad pjūvis buvo sukonstruotas (arba nubrėžta pjovimo plokštuma ir pan.), tai pirmame sprendimo etape nustatomas pjūvyje gautos figūros tipas.

Tai turi būti padaryta norint pasirinkti tinkamą skerspjūvio ploto skaičiavimo formulę. Išsiaiškinus skyriuje gautą figūros tipą ir pasirinkus formulę šios figūros plotui apskaičiuoti, pereiname tiesiai prie skaičiavimo darbo.

Kai kuriais atvejais gali būti lengviau, jei, neišsiaiškinę skyriuje gautos figūros tipo, iškart apskaičiuosite jos plotą naudodami formulę, kuri išplaukia iš teoremos.

Teorema apie daugiakampio stačiakampės projekcijos plotą: Daugiakampio stačiakampės projekcijos į plokštumą plotas lygus jo ploto ir kampo tarp daugiakampio plokštumos ir projekcijos plokštumos kosinuso sandaugai: .

Teisinga pjūvio ploto apskaičiavimo formulė yra: kur yra pjūvyje gautos figūros stačiakampės projekcijos plotas, o tai yra kampas tarp pjovimo plokštumos ir plokštumos, ant kurios projektuojama figūra. Taikant šį sprendimą, reikia sukonstruoti pjūvyje gautos figūros stačiakampę projekciją ir apskaičiuoti

Jei problemos teiginyje nurodoma, kad reikia sudaryti atkarpą ir reikia rasti gautos atkarpos plotą, tai pirmame etape pagrįstai reikia sukonstruoti nurodytą atkarpą, o tada, žinoma, nustatyti figūros tipą, gautą skyrius ir kt.

Atkreipkime dėmesį į tokį faktą: kadangi konstruojamos išgaubtų daugiakampių pjūviai, pjūvio daugiakampis taip pat bus išgaubtas, todėl jo plotą galima rasti padalijus jį į trikampius, tai yra, pjūvio plotas lygus daugiakampio plotų sumai. trikampiai, iš kurių jis sudarytas.

1 užduotis.

– taisyklingoji trikampė piramidė, kurios pagrindo kraštinė lygi, o aukštis lygus Sukonstruoti piramidės atkarpą su plokštuma, einančia per taškus, kur yra kraštinės vidurys, ir rasti jos plotą (8 pav.).

Sprendimas.

Piramidės skerspjūvis yra trikampis. Raskime jo plotą.

Kadangi piramidės pagrindas yra lygiakraštis trikampis, o taškas yra šoninės pusės vidurio taškas, tai aukštis ir tada, .

Trikampio plotą galima rasti:

2 užduotis.

Taisyklingos prizmės šoninis kraštas lygus pagrindo kraštinei. Sukurkite prizmės atkarpas su plokštumomis, einančiomis per taškąA, statmena tiesei Jei rasime gauto prizmės skerspjūvio plotą.

Sprendimas.

Sukurkime pateiktą skyrių. Padarykime tai grynai geometriniais sumetimais, pavyzdžiui, taip.

Plokštumoje, einančioje per nurodytą tiesę ir duotą tašką, nubrėžkite tiesę, statmeną tiesei, einančios per šį tašką (9 pav.). Šiuo tikslu panaudokime faktą, kad trikampyje ty jo mediana yra ir šio trikampio aukštis. Taigi tai tiesiai.

Per tašką nubrėžiame kitą tiesei statmeną liniją. Nubraižykime jį, pavyzdžiui, plokštumoje, einančioje per tiesią liniją. Akivaizdu, kad ši linija yra tiesi

Taigi, statomos dvi susikertančios tiesės, statmenos tiesei. Šios linijos apibrėžia plokštumą, einančią per tašką, statmeną tiesei, tai yra, nurodoma atsiskyrimo plokštuma.

Su šia plokštuma sukonstruokime prizmės atkarpą. Atkreipkite dėmesį, kad linija yra lygiagreti plokštumai. Tada plokštuma, einanti per tiesią liniją, kerta plokštumą išilgai tiesės, lygiagrečios tiesei, tai yra tiesia linija. Per tašką nubrėžkime tiesią liniją ir gautą tašką sujungsime tašku.

Keturkampis duota pjūvis. Nustatykime jo plotą.