Ketaksamaan dan sistem ketaksamaan dengan dua pembolehubah. Persamaan dengan dua pembolehubah dan penyelesaian geometrinya Ketaksamaan dengan dua pembolehubah dan sistemnya

22.01.2024

Selalunya perlu untuk menggambarkan pada satah koordinat satu set penyelesaian kepada ketaksamaan dengan dua pembolehubah. Penyelesaian kepada ketaksamaan dalam dua pembolehubah ialah sepasang nilai pembolehubah ini yang mengubah ketaksamaan menjadi ketaksamaan berangka sebenar.

2у+ Zx< 6.

Pertama, mari kita bina garis lurus. Untuk melakukan ini, kami menulis ketaksamaan dalam bentuk persamaan 2у+ Zx = 6 dan menyatakan y. Oleh itu, kita mendapat: y=(6-3x)/2.

Garis ini membahagikan set semua titik satah koordinat kepada titik yang terletak di atasnya dan titik yang terletak di bawahnya.

Ambil meme dari setiap kawasan titik kawalan, contohnya A (1;1) dan B (1;3)

Koordinat titik A memenuhi ketaksamaan ini 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.

Koordinat titik B tidak penuhi ketaksamaan ini 2∙3 + 3∙1< 6.

Oleh kerana ketaksamaan ini boleh menukar tanda pada garis lurus 2y + 3x = 6, maka ketaksamaan itu dipenuhi oleh set titik di rantau di mana titik A terletak. Mari kita lorekkan rantau ini.

Oleh itu, kami telah menggambarkan set penyelesaian kepada ketidaksamaan 2y + 3x< 6.

Contoh

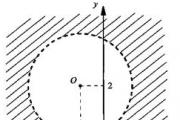
Mari kita gambarkan set penyelesaian kepada ketaksamaan x 2 + 2x + y 2 - 4y + 1 > 0 pada satah koordinat.

Mula-mula kita bina graf bagi persamaan x 2 + 2x + y 2 - 4y + 1 = 0. Mari kita pisahkan persamaan bulatan dalam persamaan ini: (x 2 + 2x + 1) + (y 2 - 4y + 4) = 4, atau (x + 1) 2 + (y - 2) 2 = 2 2 .

Ini ialah persamaan bulatan dengan pusat di titik 0 (-1; 2) dan jejari R = 2. Mari kita bina bulatan ini.

Oleh kerana ketaksamaan ini adalah ketat dan titik yang terletak pada bulatan itu sendiri tidak memenuhi ketaksamaan, kami membina bulatan dengan garis putus-putus.

Adalah mudah untuk menyemak bahawa koordinat pusat O bulatan tidak memenuhi ketaksamaan ini. Ungkapan x 2 + 2x + y 2 - 4y + 1 menukar tandanya pada bulatan yang dibina. Kemudian ketaksamaan itu dipenuhi oleh titik yang terletak di luar bulatan. Titik-titik ini dilorekkan.

Contoh

Mari kita gambarkan pada satah koordinat set penyelesaian kepada ketaksamaan

(y - x 2)(y - x - 3)< 0.

Mula-mula, mari kita bina graf bagi persamaan (y - x 2)(y - x - 3) = 0. Ia ialah parabola y = x 2 dan garis lurus y = x + 3. Mari bina garisan ini dan ambil perhatian bahawa menukar tanda ungkapan (y - x 2)(y - x - 3) berlaku hanya pada baris ini. Untuk titik A (0; 5), kita tentukan tanda ungkapan ini: (5- 3) > 0 (iaitu, ketaksamaan ini tidak berlaku). Kini mudah untuk menandakan set mata yang mana ketidaksamaan ini dipenuhi (kawasan ini berlorek).

Algoritma untuk menyelesaikan ketaksamaan dengan dua pembolehubah

1. Mari kita kurangkan ketaksamaan kepada bentuk f (x; y)< 0 (f (х; у) >0; f (x; y) ≤ 0; f (x; y) ≥ 0;)

2. Tulis kesamaan f (x; y) = 0

3. Mengenal graf yang ditulis di sebelah kiri.

4. Kami membina graf ini. Jika ketaksamaan adalah ketat (f (x; y)< 0 или f (х; у) >0), kemudian - dengan sempang, jika ketaksamaan tidak ketat (f (x; y) ≤ 0 atau f (x; y) ≥ 0), maka - dengan garis pepejal.

5. Tentukan berapa banyak bahagian grafik yang dibahagikan kepada satah koordinat

6. Pilih titik kawalan dalam salah satu bahagian ini. Tentukan tanda bagi ungkapan f (x; y)

7. Kami meletakkan papan tanda di bahagian lain pesawat, dengan mengambil kira selang seli (seperti menggunakan kaedah selang)

8. Kami memilih bahagian yang kami perlukan mengikut tanda ketidaksamaan yang kami selesaikan dan gunakan teduhan

Subjek: Persamaan dan ketaksamaan. Sistem persamaan dan ketaksamaan

Pelajaran:Persamaan dan ketaksamaan dengan dua pembolehubah

Mari kita pertimbangkan secara umum persamaan dan ketaksamaan dengan dua pembolehubah.

Persamaan dengan dua pembolehubah;

Ketaksamaan dengan dua pembolehubah, tanda ketidaksamaan boleh menjadi apa-apa;

Di sini x dan y ialah pembolehubah, p ialah ungkapan yang bergantung kepada mereka

Sepasang nombor () dipanggil penyelesaian separa bagi persamaan atau ketaksamaan sedemikian jika, apabila menggantikan pasangan ini ke dalam ungkapan, kita memperoleh persamaan atau ketaksamaan yang betul, masing-masing.

Tugasnya adalah untuk mencari atau menggambarkan pada satah set semua penyelesaian. Anda boleh menghuraikan tugasan ini - cari lokus titik (GLP), bina graf persamaan atau ketaksamaan.

Contoh 1 - selesaikan persamaan dan ketaksamaan:

Dalam erti kata lain, tugas itu melibatkan mencari GMT.

Mari kita pertimbangkan penyelesaian kepada persamaan. Dalam kes ini, nilai pembolehubah x boleh menjadi sebarang, jadi kita mempunyai:

Jelas sekali, penyelesaian kepada persamaan ialah set titik yang membentuk garis lurus

nasi. 1. Graf Persamaan Contoh 1

Penyelesaian kepada persamaan yang diberikan adalah, khususnya, titik (-1; 0), (0; 1), (x 0, x 0 +1)

Penyelesaian kepada ketaksamaan yang diberikan ialah separuh satah yang terletak di atas garisan, termasuk garisan itu sendiri (lihat Rajah 1). Sesungguhnya, jika kita mengambil sebarang titik x 0 pada baris, maka kita mempunyai kesamaan . Jika kita mengambil satu titik dalam setengah satah di atas garis, kita mempunyai . Jika kita mengambil satu titik dalam separuh satah di bawah garisan, maka ia tidak akan memuaskan ketidaksamaan kita: .

Sekarang pertimbangkan masalah dengan bulatan dan bulatan.

Contoh 2 - selesaikan persamaan dan ketaksamaan:

Kita tahu bahawa persamaan yang diberikan ialah persamaan bulatan dengan pusat pada asalan dan jejari 1.

nasi. 2. Ilustrasi contohnya 2

Pada titik arbitrari x 0, persamaan mempunyai dua penyelesaian: (x 0; y 0) dan (x 0; -y 0).

Penyelesaian kepada ketidaksamaan yang diberikan ialah satu set titik yang terletak di dalam bulatan, tidak mengambil kira bulatan itu sendiri (lihat Rajah 2).

Mari kita pertimbangkan persamaan dengan modul.

Contoh 3 - selesaikan persamaan:

Dalam kes ini, adalah mungkin untuk mengembangkan modul, tetapi kami akan mempertimbangkan spesifikasi persamaan. Adalah mudah untuk melihat bahawa graf persamaan ini adalah simetri tentang kedua-dua paksi. Kemudian jika titik (x 0 ; y 0) ialah penyelesaian, maka titik (x 0 ; -y 0) juga ialah penyelesaian, titik (-x 0 ; y 0) dan (-x 0 ; -y 0 ) juga merupakan penyelesaian .

Oleh itu, sudah cukup untuk mencari penyelesaian di mana kedua-dua pembolehubah adalah bukan negatif dan mengambil simetri tentang paksi:

nasi. 3. Ilustrasi contohnya 3

Jadi, seperti yang kita lihat, penyelesaian kepada persamaan ialah segi empat sama.

Mari kita lihat kaedah kawasan yang dipanggil menggunakan contoh khusus.

Contoh 4 - menggambarkan set penyelesaian kepada ketaksamaan:

Mengikut kaedah domain, pertama sekali kita mempertimbangkan fungsi di sebelah kiri jika terdapat sifar di sebelah kanan. Ini adalah fungsi dua pembolehubah:

Sama seperti kaedah selang, kita beralih sementara daripada ketaksamaan dan mengkaji ciri dan sifat fungsi yang digubah.

ODZ: ini bermakna paksi x sedang tercucuk.

Sekarang kita menunjukkan bahawa fungsi itu sama dengan sifar apabila pengangka pecahan itu sama dengan sifar, kita ada:

Kami membina graf fungsi.

nasi. 4. Graf fungsi, dengan mengambil kira ODZ

Sekarang pertimbangkan kawasan tanda malar fungsi; ia dibentuk oleh garis lurus dan garis putus. di dalam garisan putus terdapat kawasan D 1. Antara segmen garis putus dan garis lurus - kawasan D 2, di bawah garis - kawasan D 3, antara segmen garis putus dan garis lurus - kawasan D 4

Dalam setiap kawasan yang dipilih, fungsi itu mengekalkan tandanya, yang bermaksud ia cukup untuk memeriksa titik ujian sewenang-wenangnya di setiap kawasan.

Di kawasan itu kita ambil titik (0;1). Kami ada:

Di kawasan itu kita ambil titik (10;1). Kami ada:

Oleh itu, seluruh rantau adalah negatif dan tidak memenuhi ketidaksamaan yang diberikan.

Di kawasan itu, ambil titik (0;-5). Kami ada:

Oleh itu, seluruh wilayah adalah positif dan memenuhi ketidaksamaan yang diberikan.

Menyelesaikan ketaksamaan dalam dua pembolehubah, dan lebih-lebih lagi sistem ketaksamaan dengan dua pembolehubah, nampaknya satu tugas yang agak sukar. Walau bagaimanapun, terdapat algoritma mudah yang membantu menyelesaikan masalah yang kelihatan sangat kompleks seperti ini dengan mudah dan tanpa banyak usaha. Mari kita cuba memikirkannya.

Mari kita mempunyai ketaksamaan dengan dua pembolehubah salah satu daripada jenis berikut:

y > f(x); y ≥ f(x); y< f(x); y ≤ f(x).

Untuk menggambarkan set penyelesaian kepada ketaksamaan sedemikian pada satah koordinat, teruskan seperti berikut:

1. Kami membina graf bagi fungsi y = f(x), yang membahagikan satah kepada dua kawasan.

2. Kami memilih mana-mana kawasan yang terhasil dan mempertimbangkan titik sewenang-wenangnya di dalamnya. Kami menyemak kebolehlaksanaan ketidaksamaan asal untuk perkara ini. Jika ujian menghasilkan ketaksamaan berangka yang betul, maka kami menyimpulkan bahawa ketaksamaan asal dipenuhi di seluruh wilayah di mana titik yang dipilih berada. Oleh itu, set penyelesaian kepada ketaksamaan ialah kawasan yang menjadi milik titik yang dipilih. Jika hasil semakan adalah ketaksamaan berangka yang salah, maka set penyelesaian kepada ketaksamaan itu akan menjadi wilayah kedua di mana titik yang dipilih tidak tergolong.

3. Jika ketaksamaan adalah ketat, maka sempadan rantau, iaitu titik graf fungsi y = f(x), tidak termasuk dalam set penyelesaian dan sempadan digambarkan dengan garis putus-putus. Jika ketaksamaan tidak ketat, maka sempadan rantau, iaitu titik graf fungsi y = f(x), dimasukkan ke dalam set penyelesaian kepada ketaksamaan ini dan sempadan dalam kes ini digambarkan sebagai garis yang kukuh.
Sekarang mari kita lihat beberapa masalah mengenai topik ini.

Tugasan 1.

Apakah set mata yang diberikan oleh ketaksamaan x · y ≤ 4?

Penyelesaian.

1) Kami membina graf bagi persamaan x · y = 4. Untuk melakukan ini, kami mula-mula mengubahnya. Jelas sekali, x dalam kes ini tidak bertukar kepada 0, kerana jika tidak, kita akan mempunyai 0 · y = 4, yang tidak betul. Ini bermakna kita boleh membahagikan persamaan kita dengan x. Kami dapat: y = 4/x. Graf fungsi ini ialah hiperbola. Ia membahagikan seluruh satah kepada dua kawasan: satu di antara dua cabang hiperbola dan satu di luarnya.

2) Mari kita pilih titik arbitrari dari rantau pertama, biarkan ia titik (4; 2).
Mari kita semak ketaksamaan: 4 · 2 ≤ 4 – palsu.

Ini bermakna titik rantau ini tidak memenuhi ketidaksamaan asal. Kemudian kita boleh menyimpulkan bahawa set penyelesaian kepada ketaksamaan akan menjadi kawasan kedua di mana titik yang dipilih tidak tergolong.

3) Oleh kerana ketaksamaan tidak ketat, kita lukis titik sempadan, iaitu titik graf fungsi y = 4/x, dengan garis pepejal.

Mari kita cat set titik yang mentakrifkan ketaksamaan asal dalam warna kuning (Rajah 1).

Tugasan 2.

Lukiskan kawasan yang ditakrifkan pada satah koordinat oleh sistem
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 ≤ 9.

Penyelesaian.

Sebagai permulaan, kami membina graf bagi fungsi berikut (Gamb. 2):

y = x 2 + 2 – parabola,

y + x = 1 – garis lurus

x 2 + y 2 = 9 – bulatan.

1) y > x 2 + 2.

Kami mengambil titik (0; 5), yang terletak di atas graf fungsi.
Mari kita semak ketaksamaan: 5 > 0 2 + 2 – benar.

Akibatnya, semua titik yang terletak di atas parabola yang diberi y = x 2 + 2 memenuhi ketaksamaan pertama sistem. Mari kita cat mereka kuning.

2) y + x > 1.

Kami mengambil titik (0; 3), yang terletak di atas graf fungsi.
Mari kita semak ketaksamaan: 3 + 0 > 1 – benar.

Akibatnya, semua titik yang terletak di atas garis lurus y + x = 1 memenuhi ketaksamaan kedua sistem. Mari kita cat mereka dengan teduhan hijau.

3) x 2 + y 2 ≤ 9.

Ambil titik (0; -4), yang terletak di luar bulatan x 2 + y 2 = 9.
Mari kita semak ketaksamaan: 0 2 + (-4) 2 ≤ 9 – salah.

Oleh itu, semua titik terletak di luar bulatan x 2 + y 2 = 9, tidak memenuhi ketidaksamaan ketiga sistem. Kemudian kita boleh membuat kesimpulan bahawa semua titik yang terletak di dalam bulatan x 2 + y 2 = 9 memenuhi ketaksamaan ketiga sistem itu. Mari cat mereka dengan teduhan ungu.

Jangan lupa bahawa jika ketidaksamaan adalah ketat, maka garis sempadan yang sepadan harus dilukis dengan garis putus-putus. Kami mendapat gambar berikut (Gamb. 3).

(Gamb. 4).

Tugasan 3.

Lukiskan kawasan yang ditakrifkan pada satah koordinat oleh sistem:
(x 2 + y 2 ≤ 16;
(x ≥ -y;
(x 2 + y 2 ≥ 4.

Penyelesaian.

Sebagai permulaan, kami membina graf bagi fungsi berikut:

x 2 + y 2 = 16 – bulatan,

x = -y – garis lurus

x 2 + y 2 = 4 – bulatan (Gamb. 5).

Sekarang mari kita lihat setiap ketidaksamaan secara berasingan.

1) x 2 + y 2 ≤ 16.

Ambil titik (0; 0), yang terletak di dalam bulatan x 2 + y 2 = 16.
Mari kita semak ketaksamaan: 0 2 + (0) 2 ≤ 16 – benar.

Oleh itu, semua titik yang terletak di dalam bulatan x 2 + y 2 = 16 memenuhi ketaksamaan pertama sistem.
Mari lukis mereka dengan teduhan merah.

Kami mengambil titik (1; 1), yang terletak di atas graf fungsi.
Mari kita semak ketaksamaan: 1 ≥ -1 – benar.

Akibatnya, semua titik yang terletak di atas garis x = -y memenuhi ketaksamaan kedua sistem. Mari lukis mereka dengan teduhan biru.

3) x 2 + y 2 ≥ 4.

Ambil titik (0; 5), yang terletak di luar bulatan x 2 + y 2 = 4.
Mari kita semak ketaksamaan: 0 2 + 5 2 ≥ 4 – benar.

Akibatnya, semua titik yang terletak di luar bulatan x 2 + y 2 = 4 memenuhi ketaksamaan ketiga sistem. Mari kita lukis mereka dengan warna biru.

Dalam masalah ini, semua ketidaksamaan tidak ketat, yang bermaksud bahawa kita melukis semua sempadan dengan garis yang kukuh. Kami mendapat gambar berikut (Gamb. 6).

Kawasan carian adalah kawasan di mana ketiga-tiga kawasan berwarna bersilang antara satu sama lain (Rajah 7).

Masih ada soalan? Tidak tahu bagaimana untuk menyelesaikan sistem ketaksamaan dengan dua pembolehubah?
Untuk mendapatkan bantuan daripada tutor, daftar.
Pelajaran pertama adalah percuma!

laman web, apabila menyalin bahan sepenuhnya atau sebahagian, pautan ke sumber diperlukan.

https://accounts.google.com

Kapsyen slaid:

Ketaksamaan dengan dua pembolehubah dan sistemnya Pelajaran 1

Ketaksamaan dengan dua pembolehubah Ketaksamaan 3x – 4y  0; dan ialah ketaksamaan dengan dua pembolehubah x dan y. Penyelesaian kepada ketaksamaan dalam dua pembolehubah ialah sepasang nilai pembolehubah yang mengubahnya menjadi ketaksamaan berangka sebenar. Untuk x = 5 dan y = 3, ketaksamaan 3x - 4y  0 bertukar menjadi ketaksamaan berangka yang betul 3  0. Pasangan nombor (5;3) ialah penyelesaian kepada ketaksamaan ini. Pasangan nombor (3;5) bukan penyelesaiannya.

Adakah pasangan nombor (-2; 3) penyelesaian kepada ketaksamaan: No. 482 (b, c) Is not Is

Penyelesaian kepada ketaksamaan ialah pasangan tertib nombor nyata yang menukarkan ketaksamaan kepada ketaksamaan berangka sebenar. Secara grafik, ini sepadan dengan menentukan titik pada satah koordinat. Menyelesaikan ketidaksamaan bermakna mencari banyak penyelesaian untuknya.

Ketaksamaan dengan dua pembolehubah mempunyai bentuk: Set penyelesaian kepada ketaksamaan ialah set semua titik satah koordinat yang memenuhi ketaksamaan tertentu.

Set penyelesaian untuk ketaksamaan F(x,y) ≥ 0 x y F(x,y)≤0 x y

F(x, y)>0 F(x, y)

Peraturan titik percubaan Konstruk F(x ; y)=0 Mengambil titik percubaan dari mana-mana kawasan, tentukan sama ada koordinatnya ialah penyelesaian kepada ketaksamaan Buat kesimpulan tentang penyelesaian kepada ketaksamaan x y 1 1 2 A(1;2) F (x ; y) =0

Ketaksamaan linear dengan dua pembolehubah Ketaksamaan linear dengan dua pembolehubah dipanggil ketaksamaan dalam bentuk ax + bx +c  0 atau ax + bx +c

Cari kesilapan! No. 484 (b) -4 2 x 2 -6 y 6 -2 0 4 -2 - 4

Selesaikan secara grafik ketaksamaan: -1 -1 0 x 1 -2 y -2 2 2 1 Kami melukis graf dengan garis pepejal:

Mari tentukan tanda ketaksamaan dalam setiap kawasan -1 -1 0 x 1 -2 y -2 2 2 1 3 4 - + 1 + 2 - 7 + 6 - 5 +

Penyelesaian kepada ketaksamaan ialah satu set titik dari kawasan yang mengandungi tanda tambah dan penyelesaian kepada persamaan -1 -1 0 x 1 -2 y -2 2 2 1 3 4 - + 1 + 2 - 7 + 6 - 5 +

Mari kita selesaikan bersama No. 485 (b) No. 486 (b, d) No. 1. Tetapkan ketaksamaan dan lukis pada satah koordinat set titik yang: a) absis lebih besar daripada ordinat; b) jumlah absis dan ordinat adalah lebih besar daripada perbezaan dua kali ganda mereka.

Mari kita selesaikan bersama No. 2. Takrifkan dengan ketaksamaan satah separuh terbuka yang terletak di atas garis lurus AB yang melalui titik A(1;4) dan B(3;5). Jawapan: y  0.5x +3.5 No. 3. Untuk nilai b apakah set penyelesaian kepada ketaksamaan 3x – b y + 7  0 mewakili satah separuh terbuka yang terletak di atas garis lurus 3x – b y + 7 = 0. Jawapan: b  0.

Kerja Rumah P. 21, No 483; No. 484(c,d); No. 485(a); No. 486(c).

Pratonton:

Untuk menggunakan pratonton pembentangan, buat akaun Google dan log masuk kepadanya: https://accounts.google.com

Kapsyen slaid:

Ketaksamaan dengan dua pembolehubah dan sistemnya Pelajaran 2

Sistem ketaksamaan dengan dua pembolehubah

Penyelesaian kepada sistem ketaksamaan dengan dua pembolehubah ialah sepasang nilai pembolehubah yang mengubah setiap ketaksamaan sistem menjadi ketaksamaan berangka sebenar. No. 1. Lukiskan set penyelesaian kepada sistem ketaksamaan. No. 496 (lisan)

a) x y 2 2 x y 2 2 b)

Mari kita selesaikan bersama No. 1. Pada nilai k apakah sistem ketaksamaan mentakrifkan segitiga pada satah koordinat? Jawapan: 0

Kita selesaikan bersama-sama x y 2 2 2 2 No. 2. Rajah menunjukkan sebuah segitiga dengan bucu A(0;5), B(4;0), C(1;-2), D(-4;2). Takrifkan segi empat ini dengan sistem ketaksamaan. A B C D

Mari kita selesaikan bersama No. 3. Untuk apakah k dan b ialah set titik satah koordinat yang ditakrifkan oleh sistem ketaksamaan: a) jalur; b) sudut; c) set kosong. Jawapan: a) k= 2,b  3; b) k ≠ 2, b – sebarang nombor; c) k = 2; b

Mari kita selesaikan nombor 4 bersama-sama. Apakah angka yang diberikan oleh persamaan itu? (secara lisan) 1) 2) 3) No. 5. Lukiskan pada satah koordinat set penyelesaian titik yang ditentukan oleh ketaksamaan.

Mari kita selesaikan bersama No. 497 (c, d), 498 (c)

Kerja rumah P.22 No. 496, No. 497 (a, b), No. 498 (a, b), No. 504.

Pratonton:

Untuk menggunakan pratonton pembentangan, buat akaun Google dan log masuk kepadanya: https://accounts.google.com

Kapsyen slaid:

Ketaksamaan dengan dua pembolehubah dan sistemnya Pelajaran 3

Cari ralat! -4 2 x 2 -6 y 6 -2 0 4 -2 - 4

Cari ralat! | | | | | | | | | | | | | | | | | | 1 x y 2

Tentukan ketaksamaan 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4

0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 Tentukan ketaksamaan

0 - 3 - 1 5 3 1 2 y x - 3 - 2 1 Tentukan tanda ketaksamaan ≤

Selesaikan secara grafik sistem ketaksamaan -1 -1 0 x 1 -2 y -2 2 2 1

Ketaksamaan dan sistem ketaksamaan darjah yang lebih tinggi dengan dua pembolehubah No. 1. Lukiskan pada satah koordinat set titik yang ditentukan oleh sistem ketaksamaan

Ketaksamaan dan sistem ketaksamaan darjah yang lebih tinggi dengan dua pembolehubah No. 2. Lukiskan pada satah koordinat set titik yang ditentukan oleh sistem ketaksamaan

Ketaksamaan dan sistem ketaksamaan darjah yang lebih tinggi dengan dua pembolehubah No. 3. Lukiskan pada satah koordinat set titik yang ditentukan oleh sistem ketaksamaan. Mari kita ubah ketaksamaan pertama sistem:

Ketaksamaan dan sistem ketaksamaan darjah yang lebih tinggi dengan dua pembolehubah Kami memperoleh sistem yang setara

Ketaksamaan dan sistem ketaksamaan darjah yang lebih tinggi dengan dua pembolehubah No. 4. Lukis pada satah koordinat set titik yang ditentukan oleh sistem ketaksamaan

Mari kita putuskan bersama No. 502 Koleksi Galitsky. No. 9.66 b) y ≤ |3x -2| 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4

. No. 9.66(c) Selesaikan bersama 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 |y| ≥ 3x - 2

Kami menyelesaikan bersama No. 9.66(g) 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 |y|

Selesaikan ketaksamaan: x y -1 -1 0 1 -2 -2 2 2 1

0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 Tuliskan sistem ketaksamaan

11:11 3) Apakah angka yang ditentukan oleh set penyelesaian kepada sistem ketaksamaan? Cari luas setiap rajah. 6) Berapa banyak pasangan nombor asli adalah penyelesaian kepada sistem ketaksamaan? Kira jumlah semua nombor tersebut. Penyelesaian latihan latihan 2) Tuliskan sistem ketaksamaan dengan dua pembolehubah, set penyelesaiannya ditunjukkan dalam Rajah 0 2 x y 2 1) Lukiskan set penyelesaian sistem pada satah koordinat: 4) Takrifkan gelang ditunjukkan dalam rajah sebagai sistem ketaksamaan. 5) Selesaikan sistem ketaksamaan y x 0 5 10 5 10

Penyelesaian latihan latihan 7) Kira luas rajah yang diberikan oleh set penyelesaian kepada sistem ketaksamaan dan cari jarak terjauh antara titik rajah ini 8) Pada nilai m apakah sistem ketaksamaan hanya mempunyai satu penyelesaian? 9) Nyatakan beberapa nilai k dan b di mana sistem ketaksamaan mentakrifkan pada satah koordinat: a) jalur; b) sudut.

Ini menarik. Ahli matematik Inggeris Thomas Harriot (Harriot T., 1560-1621) memperkenalkan tanda ketidaksamaan yang biasa, dengan alasannya seperti berikut: "Jika dua segmen selari berfungsi sebagai simbol kesamaan, maka segmen bersilang mesti menjadi simbol ketidaksamaan. .” Pada tahun 1585, Harriot muda dihantar oleh Ratu England dalam ekspedisi meneroka ke Amerika Utara. Di sana dia melihat tatu yang popular di kalangan orang India dalam bentuk itu. Ini mungkin sebab Harriot mencadangkan tanda ketidaksamaan dalam dua bentuknya: “>” lebih besar daripada... dan “

Ini menarik. Simbol ≤ dan ≥ untuk perbandingan tidak ketat telah dicadangkan oleh Wallis pada tahun 1670. Pada asalnya, garisan berada di atas tanda perbandingan, dan bukan di bawahnya, seperti sekarang. Simbol-simbol ini tersebar luas selepas sokongan ahli matematik Perancis Pierre Bouguer (1734), yang daripadanya mereka memperoleh bentuk modennya.

Ketaksamaan dengan dua pembolehubahx dan y dipanggil ketaksamaan bentuk:

(atau tanda)

di manakah beberapa ungkapan dengan pembolehubah ini.

Dengan keputusan ketaksamaan dalam dua pembolehubah dipanggil pasangan nombor tertib di mana ketaksamaan ini bertukar menjadi ketaksamaan berangka sebenar.

Selesaikan ketidaksamaan- bermakna mencari set semua penyelesaiannya. Penyelesaian kepada ketaksamaan dengan dua pembolehubah ialah set titik tertentu pada satah koordinat.

Kaedah utama untuk menyelesaikan ketaksamaan ini ialah grafik kaedah. Ia terdiri daripada lukisan garisan sempadan (jika ketaksamaan adalah ketat, garisan itu dilukis dengan garis putus-putus). Kami memperoleh persamaan sempadan jika dalam ketaksamaan tertentu kami menggantikan tanda ketaksamaan dengan tanda sama. Semua garis bersama-sama membahagikan satah koordinat kepada bahagian. Set mata yang diperlukan yang sepadan dengan ketaksamaan tertentu atau sistem ketaksamaan boleh ditentukan dengan mengambil titik kawalan di dalam setiap kawasan di rantau ini.

Set ketaksamaan dengan dua pembolehubah mempunyai bentuk

Penyelesaian kepada penduduk ialah penyatuan semua penyelesaian kepada ketidaksamaan.

Contoh 1. Selesaikan sistem

Penyelesaian. Mari kita bina dalam sistem Ohoo baris yang sepadan (Gamb. 19):

Persamaan mentakrifkan bulatan berpusat di TENTANG¢(0; 1) dan R = 2.

Persamaan mentakrifkan parabola dengan bucu di TENTANG(0; 0).

Marilah kita mencari penyelesaian kepada setiap ketidaksamaan yang termasuk dalam sistem. Ketaksamaan pertama sepadan dengan kawasan di dalam bulatan dan bulatan itu sendiri (kami yakin dengan kesahihan ini jika kami menggantikan koordinat mana-mana titik dari kawasan ini ke dalam ketaksamaan). Ketaksamaan kedua sepadan dengan kawasan yang terletak di bawah parabola.