Yra keletas tipų neracionalumas trupmenomis vardiklyje. Jis siejamas su buvimu joje vienos arba algebrinės šaknies skirtingų laipsnių. Norint atsikratyti neracionalumas, būtina atlikti tam tikrus matematinius veiksmus priklausomai nuo situacijos.

Instrukcijos

1. Prieš atsikratant neracionalumas trupmenomis vardiklyje turėtumėte nustatyti jo tipą ir, atsižvelgdami į tai, tęsti sprendimą. Iš tiesų, bet koks neracionalumas kyla iš paprasto šaknų buvimo; skirtingi jų deriniai ir laipsniai nustatomi skirtingais algoritmais.

2. Vardiklio kvadratinė šaknis, formos a/?b išraiškaĮveskite papildomą koeficientą, lygų?b. Kad trupmena nesikeistų, reikia padauginti ir skaitiklį, ir vardiklį: a/?b ? (a ?b)/b.1 pavyzdys: 10/?3 ? (10?3)/3.

3. Buvimas žemiau linijos trupmenomisšaknis trupmeninė galia formos m/n ir n>mŠi išraiška atrodo taip: a/?(b^m/n).

4. Atsikratykite panašių neracionalumas taip pat įvedant daugiklį, šį kartą sunkesnį: b^(n-m)/n, t.y. iš pačios šaknies eksponento reikia atimti po jos ženklu esančios išraiškos laipsnį. Tada vardiklyje liks tik pirmasis laipsnis: a/(b^m/n) ? a ?(b^(n-m)/n)/b. 2 pavyzdys: 5/(4^3/5) ? 5?(4^2/5)/4 = 5?(16^1/5)/4.

5. Suma kvadratinės šaknys Padauginkite abu komponentus trupmenomis panašiu skirtumu. Tada iš neracionalaus šaknų pridėjimo vardiklis paverčiamas po šaknies ženklu esančių posakių/skaičių skirtumu: a/(?b + ?c) ? a (?b - ?c)/(b - c). 3 pavyzdys: 9/(?13 + ?23) ? 9 (?13-?23)/(13-23) = 9 (?23-?13)/10.

6. Kubinių šaknų suma/skirtumasKaip papildomą veiksnį pasirinkite nepilnąjį skirtumo kvadratą, jei vardiklyje yra suma, ir atitinkamai nepilną šaknų skirtumo sumos kvadratą: a/(?b ± ?c) ? a (?b? ? (b c) + ?c?)/ ((?b ± ?c) ?b? ? (b c) + ?c?) ?a (?b?? ?(b c) + ? c?)/(b ± c).4 pavyzdys: 7/(?5 +?4) ? 7 (?25-?20 +?16)/9.

7. Jei uždavinyje yra ir kvadratinės, ir kubo šaknys, tada sprendimą padalinkite į du etapus: laipsniškai išveskite iš vardiklio Kvadratinė šaknis, o po to kub. Tai daroma pagal jums jau žinomus metodus: pirmame veiksme reikia pasirinkti šaknų skirtumo/sumos daugiklį, antrajame - nepilną sumos/skirtumo kvadratą.

2 patarimas: kaip atsikratyti neracionalumo vardiklyje

Teisingas įrašas trupmeninis skaičius nėra neracionalumas V vardiklis. Tokį užrašą lengviau suprasti išvaizdos, todėl kada neracionalumas V vardiklis Protinga jo atsikratyti. Šiuo atveju iracionalumas gali tapti skaitikliu.

Instrukcijos

1. Pirmiausia pažvelkime į primityvų pavyzdį – 1/sqrt(2). Kvadratinė šaknis iš 2 yra neracionalus skaičius vardiklis.Šiuo atveju trupmenos skaitiklį ir vardiklį reikia padauginti iš vardiklio. Tai suteiks pagrįstą skaičių vardiklis. Iš tiesų, sqrt(2)*sqrt(2) = sqrt(4) = 2. Padauginus 2 identiškas kvadratines šaknis viena iš kitos, gausis tai, kas yra po visomis šaknimis: in tokiu atveju- du. Rezultatas: 1/sqrt(2) = (1*sqrt(2))/(sqrt(2)*sqrt(2)) = sqrt(2)/2. Šis algoritmas taip pat tinka trupmenoms, in vardiklis kurio šaknis padauginama iš pagrįsto skaičiaus. Skaitiklis ir vardiklis šiuo atveju turi būti padauginti iš šaknies, esančios vardiklis.Pavyzdys: 1/(2*sqrt(3)) = (1*sqrt(3))/(2*sqrt(3)*sqrt(3)) = kvadratas(3)/(2*3) = kvadratas( 3)/6.

2. Žinoma, kažkas panašaus turėtų būti padaryta, jei vardiklis Rasta ne kvadratinė šaknis, o, tarkime, kubinė šaknis ar bet koks kitas laipsnis. Įsišakniję vardiklis reikia dauginti iš tos pačios šaknies, o skaitiklis taip pat dauginamas iš tos pačios šaknies. Tada šaknis pateks į skaitiklį.

3. Sunkesniu atveju į vardiklis yra neracionaliojo ir pagrįstojo skaičiaus suma arba skirtumas arba 2 neracionalieji skaičiai. Jei suma (skirtumas) iš 2 kvadratinių šaknų arba kvadratinės šaknies ir protingo skaičiaus, galite naudoti garsiąją formulę (x+y )(x-y) = (x^2 )-(y^2). Tai padės jums atsikratyti neracionalumas V vardiklis. Jei į vardiklis skirtumas, tada skaitiklį ir vardiklį reikia padauginti iš tų pačių skaičių sumos, jei suma - tada iš skirtumo. Ši padauginta suma arba skirtumas bus vadinamas konjugatu su išraiška in vardiklis.Šios schemos rezultatas aiškiai matomas pavyzdyje: 1/(sqrt(2)+1) = (sqrt(2)-1)/(sqrt(2)+1)(sqrt(2)-1) = (sqrt(2)-1)/((sqrt(2)^2)-(1^2)) = (sqrt(2)-1)/(2-1) = kvadratas(2)-1.

4. Jei į vardiklis yra suma (skirtumas), kurioje yra šaknis didesniu mastu, tada situacija tampa nebanali ir išsivadavimas iš neracionalumas V vardiklis ne visada priimtina

3 patarimas: kaip išsivaduoti nuo neracionalumo trupmenos vardiklyje

Trupmeną sudaro skaitiklis, esantis eilutės viršuje, ir vardiklis, kurį ji padalija, esantis apačioje. Iracionalusis skaičius yra skaičius, kurio negalima pavaizduoti formoje trupmenomis su sveikuoju skaičiumi skaitiklyje ir natūraliuoju skaičiumi vardiklis. Tokie skaičiai yra, tarkime, kvadratinė šaknis iš 2 arba pi. Tradiciškai kalbant apie neracionalumą vardiklis, numanoma šaknis.

Instrukcijos

1. Pašalinkite neracionalumą padaugindami iš vardiklio. Tokiu būdu neracionalumas bus perkeltas į skaitiklį. Padauginus skaitiklį ir vardiklį iš to paties skaičiaus, reikšmė trupmenomis nesikeičia. Naudokite šią parinktį, jei kiekvienas vardiklis yra šaknis.

2. Padauginkite skaitiklį ir vardiklį iš vardiklio reikiamą skaičių kartų, priklausomai nuo šaknies. Jei šaknis kvadratas, tada vieną kartą.

3. Apsvarstykite kvadratinės šaknies pavyzdį. Paimkite trupmeną (56-y)/√(x+2). Jis turi skaitiklį (56-y) ir neracionalųjį vardiklį √(x+2), kuris yra kvadratinė šaknis.

4. Padauginkite skaitiklį ir vardiklį trupmenomisį vardiklį, tai yra į √(x+2). Pradinis pavyzdys (56-y)/√(x+2) taps ((56-y)*√(x+2))/(√(x+2)*√(x+2)). Rezultatas bus ((56-y)*√(x+2))/(x+2). Dabar šaknis yra skaitiklyje ir in vardiklis neracionalumo nėra.

5. Ne visada vardiklis trupmenomis kiekvienas yra po šaknimi. Atsikratykite neracionalumo naudodami formulę (x+y)*(x-y)=x²-y².

6. Apsvarstykite pavyzdį su trupmena (56-y)/(√(x+2)-√y). Jo neracionaliame vardiklyje yra 2 kvadratinių šaknų skirtumas. Užbaikite vardiklį, kad sudarytumėte (x+y)*(x-y).

7. Padauginkite vardiklį iš šaknų sumos. Padauginkite skaitiklį iš to paties, kad gautumėte vertę trupmenomis nepasikeitė. Trupmena bus tokia forma ((56-y)*(√(x+2)+√y))/((√(x+2)-√y)*(√(x+2)+√y) ).

8. Pasinaudokite aukščiau pateikta savybe (x+y)*(x-y)=x²-y² ir išlaisvinkite vardiklį nuo neracionalumo. Rezultatas bus ((56-y)*(√(x+2)+√y))/(x+2-y). Dabar šaknis yra skaitiklyje, o vardiklis atsikratė neracionalumo.

9. IN sunkių atvejų pakartokite abi šias parinktis, taikydami, jei reikia. Atkreipkite dėmesį, kad ne visada įmanoma atsikratyti neracionalumo vardiklis .

Algebrinė trupmena yra A/B formos išraiška, kur raidės A ir B reiškia bet kokį skaičių arba pažodiniai posakiai. Dažnai algebrinėse trupmenose skaitiklis ir vardiklis turi didžiulę formą, tačiau operacijos su tokiomis trupmenomis turėtų būti atliekamos pagal tas pačias taisykles, kaip ir veiksmai su paprastomis, kai skaitiklis ir vardiklis yra teigiami sveikieji skaičiai.

Instrukcijos

1. Jei duodamas sumaišytas trupmenomis, paverskite jas netaisyklingomis trupmenomis (trupmenomis, kuriose skaitiklis didesnis už vardiklį): padauginkite vardiklį iš visos dalies ir pridėkite skaitiklį. Taigi skaičius 2 1/3 pavirs į 7/3. Norėdami tai padaryti, padauginkite 3 iš 2 ir pridėkite vieną.

2. Jei jums reikia konvertuoti dešimtainę į netinkamą trupmeną, pagalvokite, kaip skaičių be kablelio padalyti iš vieneto su tiek nulių, kiek yra skaičių po kablelio. Tarkime, įsivaizduokime skaičių 2,5 kaip 25/10 (jei jį sutrumpinsite, gausite 5/2), o skaičių 3,61 – kaip 361/100. Naudoti netinkamas trupmenas dažnai yra lengviau nei su mišriomis ar dešimtainėmis trupmenomis.

3. Jei trupmenos vardikliai yra vienodi ir jums reikia juos pridėti, tiesiog pridėkite skaitiklius; vardikliai lieka nepakitę.

4. Jei reikia atimti trupmenas su identiškais vardikliais, iš pirmosios trupmenos skaitiklio atimkite 2-osios trupmenos skaitiklį. Vardikliai taip pat nesikeičia.

5. Jei reikia pridėti trupmenas arba atimti vieną trupmeną iš kitos, o jos turi skirtingus vardiklius, sumažinkite trupmenas iki bendro vardiklio. Norėdami tai padaryti, suraskite skaičių, kuris bus mažiausias universalus abiejų vardiklių kartotinis (LCM) arba keli, jei trupmenos didesnės nei 2. LCM yra skaičius, kuris bus padalintas į visų pateiktų trupmenų vardiklius. Pavyzdžiui, 2 ir 5 šis skaičius yra 10.

6. Po lygybės ženklo nubrėžkite horizontalią liniją ir į vardiklį įrašykite šį skaičių (NOC). Prie viso termino pridėkite papildomų veiksnių – skaičių, iš kurio reikia padauginti ir skaitiklį, ir vardiklį, kad gautumėte LCM. Žingsnis po žingsnio padauginkite skaitiklius iš papildomų koeficientų, išsaugodami sudėjimo arba atimties ženklą.

7. Apskaičiuokite bendrą sumą, jei reikia, sumažinkite arba pasirinkite visą dalį. Pavyzdžiui, ar reikia jį sulankstyti? Ir?. Abiejų trupmenų LCM yra 12. Tada pirmosios trupmenos papildomas koeficientas yra 4, o antrosios trupmenos – 3. Iš viso: ?+?=(1·4+1·3)/12=7/12.

8. Jei pateikiamas daugybos pavyzdys, padauginkite skaitiklius kartu (tai bus sumos skaitiklis) ir vardiklius (tai bus sumos vardiklis). Šiuo atveju nereikia jų redukuoti iki bendro vardiklio.

9. Norėdami padalyti trupmeną iš trupmenos, turite apversti antrąją trupmeną ir padauginti trupmenas. Tai yra, a/b: c/d = a/b · d/c.

10. Jei reikia, koeficientuokite skaitiklį ir vardiklį. Pvz., Iškelkite universalųjį koeficientą iš skliausto arba išplėskite jį pagal sutrumpintas daugybos formules, kad po to, jei reikia, galėtumėte sumažinti skaitiklį ir vardiklį GCD - minimaliu universaliuoju dalikliu.

Pastaba!
Sudėkite skaičius su skaičiais, tos pačios rūšies raides su tos pačios rūšies raidėmis. Tarkime, neįmanoma pridėti 3a ir 4b, vadinasi, jų suma arba skirtumas liks skaitiklyje – 3a±4b.

Kasdieniame gyvenime dažniau pasitaiko netikri skaičiai: 1, 2, 3, 4 ir kt. (5 kg bulvių), ir trupmeniniai, ne sveikieji skaičiai (5,4 kg svogūnų). Daugelis jų pristatomi forma po kablelio. Bet pavaizduokite dešimtainę trupmeną forma trupmenomis gana lengva.

Instrukcijos

1. Tarkime, duotas skaičius „0,12“. Jei nesumažinsite šios dešimtainės trupmenos ir nepateiksite jos tokios, kokia yra, tada ji atrodys taip: 12/100 („dvylika šimtųjų“). Norint atsikratyti šimto vardiklyje, tiek skaitiklį, tiek vardiklį reikia padalyti iš skaičiaus, kuris padalija juos į sveikuosius skaičius. Šis skaičius yra 4. Tada padalijus skaitiklį ir vardiklį, gauname skaičių: 3/25.

2. Jei labiau pažvelgtume į kasdienybę, dažnai ant produktų kainų etiketės pamatytume, kad jos svoris yra, pavyzdžiui, 0,478 kg ar pan.. Šį skaičių taip pat nesunku įsivaizduoti forma trupmenomis:478/1000 = 239/500. Ši trupmena yra gana negraži, o jei būtų tikimybė, tada šią dešimtainę trupmeną būtų leista dar sumažinti. Ir viskas vienodai: pasirenkamas skaičius, dalinantis ir skaitiklį, ir vardiklį. Šis skaičius vadinamas didžiausiu universaliu faktoriumi. Koeficientas pavadintas „didžiausiu“, nes daug patogiau iš karto padalyti skaitiklį ir vardiklį iš 4 (kaip pirmame pavyzdyje), nei du kartus iš 2.

Video tema

Dešimtainė trupmena- įvairovė trupmenomis, kurio vardiklyje yra „apvalus“ skaičius: 10, 100, 1000 ir tt, tarkime, trupmena 5/10 dešimtainis žymėjimas yra 0,5. Remiantis šia disertacija, trupmena gali būti pavaizduotas kaip dešimtainis skaičius trupmenomis .

Instrukcijos

1. Galimas, turi būti pateikiamas kaip dešimtainis skaičius trupmena 18/25. Pirmiausia turite įsitikinti, kad vardiklyje yra vienas iš „apvalių“ skaičių: 100, 1000 ir kt. Norėdami tai padaryti, vardiklį reikia padauginti iš 4. Tačiau tiek skaitiklį, tiek vardiklį turėsite padauginti iš 4.

2. Skaitiklio ir vardiklio dauginimas trupmenomis 18/25 iš 4, pasirodo, 72/100. Tai įrašyta trupmena dešimtaine forma: 0,72.

Dalinant 2 trupmenas po kablelio, kai po ranka nėra skaičiuoklės, daugelis patiria tam tikrų sunkumų. Čia tikrai nėra nieko sunkaus. Dešimtainė trupmenomis vadinami tokiais, jei jų vardiklyje yra skaičius, kuris yra 10 kartotinis. Kaip įprasta, tokie skaičiai rašomi vienoje eilutėje ir turi kablelį, skiriantį trupmeninę dalį nuo visumos. Matyt, dėl trupmeninės dalies, kuri skiriasi ir skaitmenų skaičiumi po kablelio, daugeliui neaišku, kaip be skaičiuotuvo atlikti matematinius veiksmus su tokiais skaičiais.

Jums reikės

• popieriaus lapas, pieštukas

Instrukcijos

1. Pasirodo, norint padalyti vieną dešimtainę trupmeną iš kitos, reikia pažvelgti į abu skaičius ir nustatyti, kuris iš jų turi daugiau skaitmenų po kablelio. Abu skaičius padauginame iš skaičiaus, kuris yra 10 kartotinis, t.y. 10, 1000 arba 100 000, kurių nulių skaičius yra lygus daugiau skaitmenys vėliau nei vieno iš 2 mūsų pradinių skaičių dešimtainis taškas. Dabar abu yra dešimtainiai trupmenomis paversti įprastais sveikaisiais skaičiais. Paimkite popieriaus lapą pieštuku ir gautus du skaičius atskirkite „kampu“. Gauname rezultatą.

2. Tarkime, kad skaičių 7,456 reikia padalyti iš 0,43. Pirmas skaičius turi daugiau skaitmenų po kablelio (3 skaitmenys po kablelio), todėl abu skaičius padauginame ne iš 1000 ir gauname du primityvius sveikuosius skaičius: 7456 ir 430. Dabar 7456 padalijame iš 430 su „kampu“ ir gauname, kad jei 7,456 yra padalintas iki 0.43 išeis maždaug 17.3.

3. Yra dar vienas padalijimo būdas. Dešimtainių skaičių užrašymas trupmenomis primityviųjų trupmenų pavidalu su skaitikliu ir vardikliu, mūsų atveju tai yra 7456/1000 ir 43/100. Vėliau užrašome 2 primityviųjų trupmenų padalijimo išraišką: 7456*100/1000*43, po to sumažiname dešimtukus, gauname: 7456/10*43 = 7456/430 Galutinėje išvestyje vėl gauname dalijimą 2 primityvūs skaičiai 7456 ir 430, kuriuos galima padaryti su „kampu“.

Video tema

Naudingas patarimas
Taigi dešimtaines trupmenas padalinti galima sumažinti iki sveikųjų skaičių, padauginus kiekvieną iš jų iš to paties skaičiaus. Veiksmų su sveikaisiais skaičiais atlikimas, kaip įprasta, niekam nesukelia sunkumų.

Video tema

Transformuojant trupmeninę algebrinę išraišką, kurios vardiklyje yra neracionali išraiška, dažniausiai bandoma pavaizduoti trupmeną taip, kad jos vardiklis būtų racionalus. Jei A, B, C, D,... yra keletas algebrinės išraiškos, tada galite nurodyti taisykles, kurių pagalba galite atsikratyti radikalių ženklų formos posakių vardiklyje

Visais šiais atvejais išsivadavimas iš neracionalumo pasiekiamas trupmenos skaitiklį ir vardiklį padauginus iš koeficiento, pasirinkto taip, kad jo sandauga iš trupmenos vardiklio būtų racionali.

1) Atsikratyti neracionalumo formos trupmenos vardiklyje. Padauginkite skaitiklį ir vardiklį iš

1 pavyzdys.

2) Formos trupmenoms . Padauginkite skaitiklį ir vardiklį iš neracionalaus koeficiento

atitinkamai, ty į konjuguotą iracionaliąją išraišką.

Paskutinio veiksmo prasmė ta, kad vardiklyje sumos ir skirtumo sandauga paverčiama kvadratų skirtumu, kuris jau bus racionali išraiška.

2 pavyzdys. Išsilaisvinkite nuo neracionalumo išraiškos vardiklyje:

Sprendimas, a) Padauginkite trupmenos skaitiklį ir vardiklį iš išraiškos . Mes gauname (su sąlyga)

3) Esant tokiems posakiams kaip

vardiklis traktuojamas kaip suma (skirtumas) ir padauginamas iš skirtumo (sumos) dalinio kvadrato, kad būtų gauta kubų ((20.11), (20.12)) suma (skirtumas). Skaitiklis taip pat dauginamas iš to paties koeficiento.

3 pavyzdys. Išsilaisvinkite nuo neracionalumo posakių vardiklyje:

Sprendimas, a) Laikydami šios trupmenos vardiklį skaičių ir 1 suma, padauginkite skaitiklį ir vardiklį iš šių skaičių skirtumo dalinio kvadrato:

arba galiausiai:

Kai kuriais atvejais reikia atlikti priešingo pobūdžio transformaciją: išlaisvinti trupmeną nuo skaitiklio neracionalumo. Tai atliekama lygiai taip pat.

4 pavyzdys. Išlaisvinkite save nuo neracionalumo trupmenos skaitiklyje.

Pamoka Nr. 1 Pamokos tema: „Išsivadavimas nuo neracionalumo trupmenos vardiklyje“

Tikslai:

Švietimas:

Vystomasis:

Švietimas: skatinant jūsų veiksmų nuoseklumą.

Pamokos tipas: mokytis naujų dalykų

Pamokos standartas:

sugebėti rasti būdą, kaip atsikratyti neracionalumo

suprasti „sujungtos išraiškos“ reikšmę

sugebėti atsikratyti iracionalumo vardiklyje.

Įranga: kortelės savarankiškam darbui.

Per užsiėmimus

Ar žinote, kaip išgauti šaknis? – klausia mokytoja

Taip, žinoma. Jums reikia stipriau ištraukti augalo stiebą, ir jo šaknis bus pašalinta iš dirvožemio.

Ne, aš turėjau omenyje kitą šaknį, pavyzdžiui, iš devynių.

Tai bus „devyni“, nes „th“ yra priesaga.

Turiu omenyje kvadratinę šaknį.

Kvadratinių šaknų nėra. Jie yra pluoštiniai ir panašūs į lazdeles.

Aritmetinė kvadratinė šaknis iš devynių.

Štai ką jie pasakytų! Kvadratinė šaknis iš devynių = 3!

Ar žinote, kaip išgauti šaknis?

2. „Kartojimas yra mokymosi motina“.

(8 min.)

2.Namo/namo patikra№ 168 1)4; 2)10; 3)4;4) 8

3.Apšilti. Atlikite veiksmus (1 skaidrė). Patikrinkite ratu prieš laikrodžio rodyklę.

1. Pasirinkite nežinomą veiksnį (2 skaidrė)

Suskirstymas į grupes: pagal pasirinktus paveikslus.

Patikrinkite pakaitinių kompozicijų poras.

Jie dirba individualiai ir tikrina, vertina taškus.

(1 priedas)

3. „Knyga yra knyga, bet naudok savo smegenis“ (5 minutės)

(3 skaidrė) Du draugai išsprendė lygtį
ir gavo skirtingus atsakymus. Vienas iš jų pasirinko x = , atliko patikrinimą. Antrasis nustatė nežinomą veiksnį, padalijus produktą iš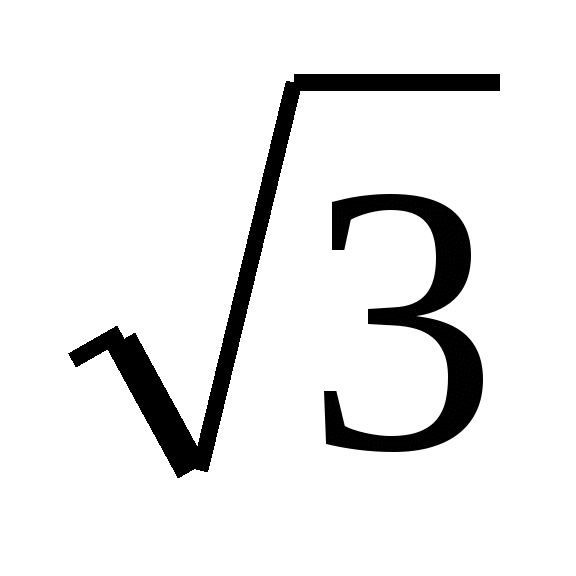
ir gavosi x = 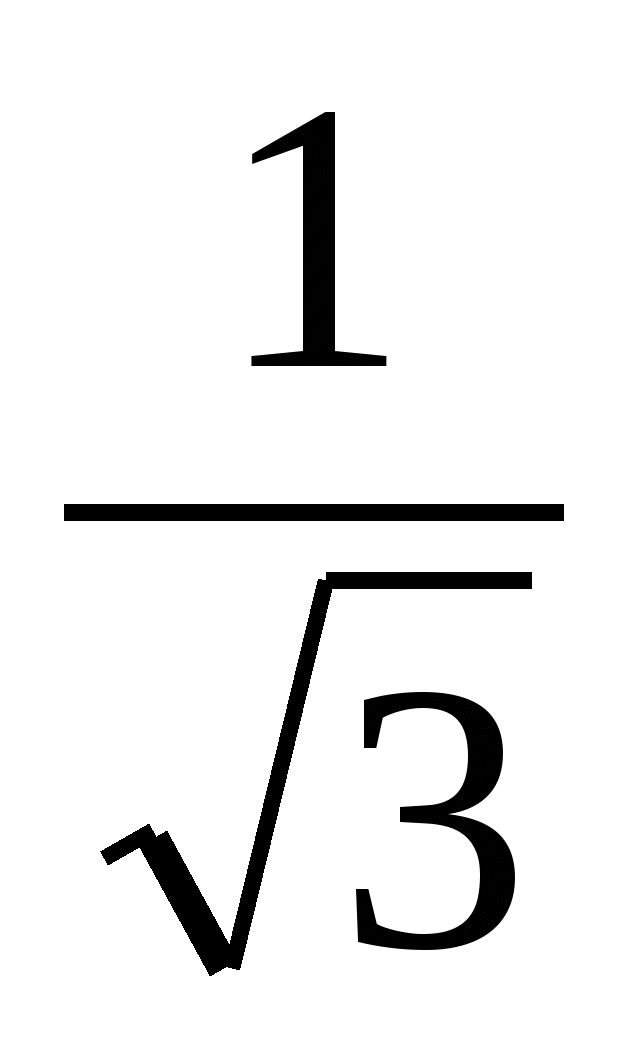. Kuris teisingas? Gali tiesinė lygtis turi dvi šaknis? Patogiausia skaičiavimo išraiška yra ta, kurios vardiklyje nėra neracionalumo.

Pamokos tema(4 skaidrė) : Išsivadavimas iš iracionalumo trupmenos vardiklyje

Tikslai(5 skaidrė) : susipažinti su būdais, kaip atsikratyti neracionalumo trupmenos vardikliuose. Sugebėjimo išlaisvinti vardiklį nuo neracionalumo ugdymas;

Išspręskite ir patikrinkite pamainų poras.

Jie aptaria situaciją ir daro išvadą.

Užsirašykite temą

Formuluoti tikslus: susipažinti su būdais, kaip atsikratyti neracionalumo trupmenos vardikliuose.

ugdyti gebėjimą nustatyti būdą išsivaduoti iš neracionalumo;

4. Darbas su nauja medžiaga.

(10 min.)

Kaip atsikratyti neracionalumo vardiklyje? Ar tu nori žinoti?

Darbas grupėse prie naujos medžiagos

Grupės pasirodymas

Prisegimas (6 skaidrė)

Jie dirba su pagalbiniu kontūru. (2 priedas)

Išspręskite pavyzdžius.

(3 priedas)

Keistis informacija.

5. Įkrovimas (3 min.)

Darydamas pratimus

6. Savarankiškas darbas

(10 min.)

Kelių lygių kortelėmis

1 colio:

2 colių:

3 colių:

Atlikite individualiai, patikrinkite keisdami sąsiuvinius su kita grupe.

Taškai įrašomi į grupės rezultatų kortelę.

(1 priedas)

7.Kūrybinė užduotis

(2 minutės)

Beždžionė – oranžinė pardavėja (7 skaidrė)

Kartą atvykęs į savo vasarnamį,

Radau problemą su radikalais.

Ji pradėjo juos mėtyti visur.

Mes prašome jūsų, merginos ir berniukai,

Išspręskite beždžionės uodegos problemą.

Ar manote, kad baigėme studijuoti šią temą? Tęskime kitą pamoką.

Jie kalba apie tai, ką apie tai sužinos kitoje pamokoje.

8. Namų darbai: (2 minutės)

19 p. (7 skaidrė)

1 lygis: Nr. 170 (1–6)

2 lygis: Nr. 170 (1–6 ir 9,12)

Kūrybinė užduotis: Martyškino užduotis.

Užsirašyti

9. Pamokos santrauka. Atspindys

(3 min.)

Prie pasirinkto jaustuko pritvirtintos dvi žvaigždės ir palinkėjimas ant lipdukų (7 skaidrė)

Taškai paverčiami pažymiais ir mokytojui įteikiama grupės balų kortelė.

1 PRIEDAS

Grupės rezultatų kortelė.

0-8 taškai

Pasirinkite daugiklį

0-8 taškai

Darbas grupėje prie naujos medžiagos

0-5 taškai

Aš pats. Darbas

0-5 taškai

Pamokos veikla

0-5 taškai

2 PRIEDAS

Pagalbiniai užrašai

Jei vardiklis algebrinė trupmena yra kvadratinės šaknies ženklas, tada sakoma, kad vardiklyje yra neracionalumo. Išraiškos pavertimas tokia forma, kad trupmenos vardiklyje nebūtų kvadratinės šaknies ženklų, vadinamas išsivadavimas iš iracionalumo vardiklyje

Šioje temoje apžvelgsime visas tris aukščiau išvardytas neracionalumo ribų grupes. Pradėkime nuo ribų, kuriose yra $\frac(0)(0)$ formos neapibrėžtis.

Neapibrėžtumo atskleidimas $\frac(0)(0)$.

Sprendimo schema standartiniai pavyzdžiaiŠis tipas paprastai susideda iš dviejų etapų:

• Iracionalumo, sukėlusio neapibrėžtumą, atsikratome daugindami iš vadinamosios „konjuguotos“ išraiškos;
• Jei reikia, išreikškite išraišką skaitiklyje arba vardiklyje (arba abu);
• Sumažiname veiksnius, lemiančius neapibrėžtumą, ir apskaičiuojame norimą ribos reikšmę.

Aukščiau vartojamas terminas "konjuguota išraiška" bus išsamiai paaiškintas pavyzdžiuose. Kol kas nėra jokios priežasties apie tai išsamiai kalbėti. Apskritai galite eiti kitu keliu, nenaudodami konjuguotos išraiškos. Kartais tinkamai parinktas pakaitalas gali panaikinti neracionalumą. Tokie pavyzdžiai standartuose yra reti bandymai, todėl pakeitimo naudojimui nagrinėsime tik vieną pavyzdį Nr.6 (žr. antrąją šios temos dalį).

Mums reikės kelių formulių, kurias parašysiu žemiau:

\pradžia(lygtis) a^2-b^2=(a-b)\cdot(a+b) \end(lygtis) \pradžia(lygtis) a^3-b^3=(a-b)\cdot(a^2) +ab+b^2) \pabaiga(lygtis) \begin(lygtis) a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end(lygtis) \begin (lygtis) a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end(lygtis)

Be to, darome prielaidą, kad skaitytojas žino kvadratinių lygčių sprendimo formules. Jei $x_1$ ir $x_2$ yra šaknys kvadratinis trinaris$ax^2+bx+c$, tada jį galima koeficientuoti naudojant šią formulę:

\begin(lygtis) ax^2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end(lygtis)

Formulių (1)-(5) visiškai pakanka standartiniams uždaviniams spręsti, prie kurių dabar pereisime.

1 pavyzdys

Raskite $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)$.

Kadangi $\lim_(x\to 3)(\sqrt(7-x)-2)=\sqrt(7-3)-2=\sqrt(4)-2=0$ ir $\lim_(x\ to 3) (x-3)=3-3=0$, tada duotoje riboje turime formos $\frac(0)(0)$ neapibrėžtį. Skirtumas $\sqrt(7-x)-2$ neleidžia mums atskleisti šio neapibrėžtumo. Norint atsikratyti tokių neracionalumų, naudojamas dauginimas iš vadinamosios „konjuguotos išraiškos“. Dabar pažiūrėsime, kaip veikia toks dauginimas. Padauginkite $\sqrt(7-x)-2$ iš $\sqrt(7-x)+2$:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)$$

Norėdami atidaryti skliaustus, taikykite , pakeisdami $a=\sqrt(7-x)$, $b=2$ į dešinę minėtos formulės pusę:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)=(\sqrt(7-x))^2-2^2=7-x-4=3-x .$$

Kaip matote, jei skaitiklį padauginsite iš $\sqrt(7-x)+2$, tada šaknis (ty neracionalumas) skaitiklyje išnyks. Ši išraiška $\sqrt(7-x)+2$ bus konjugatasį išraišką $\sqrt(7-x)-2$. Tačiau negalime tiesiog skaitiklio padauginti iš $\sqrt(7-x)+2$, nes tai pakeis trupmeną $\frac(\sqrt(7-x)-2)(x-3)$, kuri yra žemiau ribos. Vienu metu turite padauginti ir skaitiklį, ir vardiklį:

$$ \lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)= \left|\frac(0)(0)\right|=\lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt(7-x)+2)) $$

Dabar atsiminkite, kad $(\sqrt(7-x)-2)(\sqrt(7-x)+2)=3-x$ ir atidarykite skliaustus. O atidarę skliaustus ir nedidelę transformaciją $3-x=-(x-3)$, trupmeną sumažiname $x-3$:

$$ \lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt( 7-x)+2))= \lim_(x\iki 3)\frac(3-x)((x-3)\cdot(\sqrt(7-x)+2))=\\ =\lim_ (x\iki 3)\frac(-(x-3))((x-3)\cdot(\sqrt(7-x)+2))= \lim_(x\iki 3)\frac(-1 )(\sqrt(7-x)+2) $$

Neapibrėžtis $\frac(0)(0)$ išnyko. Dabar galite lengvai gauti atsakymą iš šio pavyzdžio:

$$ \lim_(x\to 3)\frac(-1)(\sqrt(7-x)+2)=\frac(-1)(\sqrt(7-3)+2)=-\frac( 1)(\sqrt(4)+2)=-\frac(1)(4).$$

Pastebiu, kad konjuguota išraiška gali pakeisti savo struktūrą, priklausomai nuo to, kokį neracionalumą ji turėtų pašalinti. 4 ir 5 pavyzdžiuose (žr. antrąją šios temos dalį) bus naudojama kitokio tipo konjuguota išraiška.

Atsakymas: $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)=-\frac(1)(4)$.

2 pavyzdys

Raskite $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$.

Nuo $\lim_(x\to 2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\sqrt(2^2+5)-\sqrt(7\cdot 2 ^ 2-19)=3-3=0$ ir $\lim_(x\to 2)(3x^2-5x-2)=3\cdot2^2-5\cdot 2-2=0$, tada mes yra susiję su $\frac(0)(0)$ formos neapibrėžtumu. Atsikratykime iracionalumo šios trupmenos vardiklyje. Norėdami tai padaryti, pridedame trupmenos $\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$ skaitiklį ir vardiklį. išraiška $\sqrt(x^ 2+5)+\sqrt(7x^2-19)$ konjugata su vardikliu:

$$ \lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\left|\frac(0 )(0)\right|= \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))) ((\sqrt(x^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))) $$

Vėlgi, kaip pavyzdyje Nr. 1, norėdami išplėsti, turite naudoti skliaustus. Dešinėje minėtos formulės pusėje pakeitę $a=\sqrt(x^2+5)$, $b=\sqrt(7x^2-19)$, gauname tokią vardiklio išraišką:

$$ \left(\sqrt(x^2+5)-\sqrt(7x^2-19)\right)\left(\sqrt(x^2+5)+\sqrt(7x^2-19)\ dešinė)=\\ =\left(\sqrt(x^2+5)\right)^2-\left(\sqrt(7x^2-19)\right)^2=x^2+5-(7x) ^2-19)=-6x^2+24=-6\cdot(x^2-4) $$

Grįžkime prie savo ribos:

$$ \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))((\sqrt(x) ^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19)))= \lim_(x\to 2)\frac( (3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))(-6\cdot(x^2-4))=\\ =-\ frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x^2-4) $$

Pavyzdyje Nr. 1, beveik iš karto po padauginimo iš konjugato išraiškos, frakcija buvo sumažinta. Čia prieš sumažinimą turėsite suskaidyti išraiškas $3x^2-5x-2$ ir $x^2-4$ ir tik tada pereiti prie mažinimo. Norėdami suskaičiuoti išraišką $3x^2-5x-2$, turite naudoti . Pirmiausia apsispręskime kvadratinė lygtis$3x^2-5x-2=0$:

$$ 3x^2-5x-2=0\\ \begin(lygiuotas) & D=(-5)^2-4\cdot3\cdot(-2)=25+24=49;\\ & x_1=\ frac(-(-5)-\sqrt(49))(2\cdot3)=\frac(5-7)(6)=-\frac(2)(6)=-\frac(1)(3) ;\\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot3)=\frac(5+7)(6)=\frac(12)(6)=2. \end(sulygiuotas) $$

Pakeitę $x_1=-\frac(1)(3)$, $x_2=2$ į , turėsime:

$$ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)(x-2)=3\cdot\left(x+\ frac(1)(3)\dešinė)(x-2)=\kairysis(3\cdot x+3\cdot\frac(1)(3)\right)(x-2) =(3x+1)( x-2). $$

Dabar atėjo laikas faktorinizuoti išraišką $x^2-4$. Naudokime , pakeisdami $a=x$, $b=2$:

$$ x^2-4=x^2-2^2=(x-2)(x+2) $$

Pasinaudokime gautais rezultatais. Kadangi $x^2-4=(x-2)(x+2)$ ir $3x^2-5x-2=(3x+1)(x-2)$, tada:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2 -19)))(x^2-4) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x) ^2+5)+\sqrt(7x^2-19)))((x-2)(x+2)) $$

Sumažinus skliausteliu $x-2$ gauname:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x^2+5)+\sqrt(7x^ 2-19)))((x-2)(x+2)) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt( x^2+5)+\sqrt(7x^2-19)))(x+2). $$

Viskas! Nežinomybė dingo. Dar vienas žingsnis ir pasiekiame atsakymą:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x+2)=\\ =-\frac(1)(6)\cdot\frac((3\cdot 2+1)(\sqrt(2^2+5)+\sqrt(7\cdot 2) ^2-19)))(2+2)= -\frac(1)(6)\cdot\frac(7(3+3))(4)=-\frac(7)(4). $$

Atsakymas: $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=-\frac(7)( 4) $.

Toliau pateiktame pavyzdyje apsvarstykite atvejį, kai iracionalumo bus ir trupmenos skaitiklyje, ir vardiklyje.

3 pavyzdys

Raskite $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))$.

Nuo $\lim_(x\to 5)(\sqrt(x+4)-\sqrt(x^2-16))=\sqrt(9)-\sqrt(9)=0$ ir $\lim_( x \to 5)(\sqrt(x^2-3x+6)-\sqrt(5x-9))=\sqrt(16)-\sqrt(16)=0$, tada turime formos $ neapibrėžtį \frac (0)(0)$. Kadangi šiuo atveju šaknys yra ir vardiklyje, ir skaitiklyje, norėdami atsikratyti neapibrėžtumo, turėsite padauginti iš dviejų skliaustų iš karto. Pirma, su išraiška $\sqrt(x+4)+\sqrt(x^2-16)$ susiekite su skaitikliu. Ir antra, prie išraiškos $\sqrt(x^2-3x+6)-\sqrt(5x-9)$ konjugatas su vardikliu.

$$ \lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=\left|\frac(0)(0)\right|=\\ =\lim_(x\to 5)\frac((\sqrt(x+4)-\sqrt(x^2-16) )(\sqrt(x+4)+\sqrt(x^2-16))(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((\sqrt(x^2) -3x+6)-\sqrt(5x-9))(\sqrt(x^2-3x+6)+\sqrt(5x-9))(\sqrt(x+4)+\sqrt(x^2) -16))) $$ $$ -x^2+x+20=0;\\ \begin(lygiuotas) & D=1^2-4\cdot(-1)\cdot 20=81;\\ & x_1=\frac(-1-\sqrt(81))(-2)=\frac(-10)(-2)=5;\\ & x_2=\frac(-1+\sqrt(81))( -2)=\frac(8)(-2)=-4. \end(sulygiuotas) \\ -x^2+x+20=-1\cdot(x-5)(x-(-4))=-(x-5)(x+4). $$

Už išraišką $x^2-8x+15$ gauname:

$$ x^2-8x+15=0;\\ \begin(sulygintas) & D=(-8)^2-4\cdot 1\cdot 15=4;\\ & x_1=\frac(-(- 8)-\sqrt(4))(2)=\frac(6)(2)=3;\\ & x_2=\frac(-(-8)+\sqrt(4))(2)=\frac (10) (2) = 5. \end(sulygiuotas)\\ x^2+8x+15=1\cdot(x-3)(x-5)=(x-3)(x-5). $$

Riboje pakeičiant gautus išplėtimus $-x^2+x+20=-(x-5)(x+4)$ ir $x^2+8x+15=(x-3)(x-5)$ svarstoma, turės:

$$ \lim_(x\iki 5)\frac((-x^2+x+20)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x^2) -8x+15)(\sqrt(x+4)+\sqrt(x^2-16)))= \lim_(x\to 5)\frac(-(x-5)(x+4)(\ sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3)(x-5)(\sqrt(x+4)+\sqrt(x^2-16)) )=\\ =\lim_(x\iki 5)\frac(-(x+4)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3) (\sqrt(x+4)+\sqrt(x^2-16)))= \frac(-(5+4)(\sqrt(5^2-3\cdot 5+6)+\sqrt(5) \cdot 5-9)))((5-3)(\sqrt(5+4)+\sqrt(5^2-16)))=-6. $$

Atsakymas: $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=-6 USD.

Kitoje (antroje) dalyje apžvelgsime dar porą pavyzdžių, kuriuose konjuguota išraiška turės kitokią formą nei ankstesnėse problemose. Svarbiausia atsiminti, kad konjuguoto posakio naudojimo tikslas yra atsikratyti neracionalumo, sukeliančio netikrumą.

Jūsų pageidavimu!

5. Išspręskite nelygybę:

6 . Supaprastinkite išraišką:

17. f(x)=6x2 +8x+5, F(-1)=3. Raskite F(-2).

Raskime C, žinodami, kad F(-1) = 3.

3 = 2 ∙ (-1) 3 + 4 ∙ (-1) 2 + 5 ∙ (-1) + C;

3 = -2 + 4 - 5 + C;

Taigi, antidarinė F(x) = 2x 3 + 4x 2 + 5x + 6. Raskime F(-2).

F(-2) = 2∙(-2) 3 +4∙(-2) 2 +5∙(-2)+6 = -16+16-10+6=-4.

20. Atsikratykite neracionalumo vardiklyje

Sprendimas pagrįstas pagrindine trupmenos savybe, leidžiančia trupmenos skaitiklį ir vardiklį padauginti iš to paties skaičiaus, kuris skiriasi nuo nulio. Norėdami atsikratyti radikalių ženklų trupmenos vardiklyje, dažniausiai naudojamos sutrumpintos daugybos formulės. Juk jei dviejų radikalų skirtumas padauginamas iš jų sumos, tai gauname šaknų kvadratų skirtumą, t.y. gausite išraišką be radikalių ženklų.

21. Supaprastinkite išraišką:

Išspręskime šį pavyzdį dviem būdais. 1) Įsivaizduokime antrojo veiksnio radikaliąją išraišką dviejų išraiškų sumos kvadrato pavidalu, t.y. forma (a + b) 2 . Tai leis mums išgauti aritmetinę kvadratinę šaknį.

2) Padėkime pirmąjį koeficientą kvadratu ir padėkite jį po antrojo koeficiento aritmetinės kvadratinės šaknies ženklu.

Apsispręskite taip, kaip jums patogu!

22. Raskite (x 1 ∙y 1 +x 2 ∙y 2), kur (x n; y n) yra lygčių sistemos sprendiniai:

Kadangi aritmetinė kvadratinė šaknis gali būti paimta tik iš neneigiamo skaičiaus, tada priimtinos vertės kintamasis adresu visi skaičiai, tenkinantys nelygybę y≥0. Kadangi sandauga pirmoje sistemos lygtyje yra lygi neigiamas skaičius, tada turi būti įvykdyta ši sąlyga: x<0 . Išreikškime X iš pirmosios lygties ir jos reikšmę pakeiskite antrąja lygtimi. Išspręskime gautą lygtį for adresu, tada raskite vertes X, atitinkantis anksčiau gautas reikšmes adresu.

23. Išspręskite nelygybę: 7sin 2 x+cos 2 x>5sinx.

Kadangi pagal pagrindinį trigonometrinį tapatumą: sin 2 x+cos 2 x=1, tai pateikiant šią nelygybę forma 6sin 2 x+ sin 2 x +cos 2 x>5sinx ir taikant pagrindinį trigonometrinė tapatybė, gauname: 6sin 2 x+ 1>5sinx. Nelygybės sprendimas:

6sin 2 x-5sinx+1 >0. Pakeiskime sinx=y ir gaukime kvadratinę nelygybę:

6m 2 -5m+1>0. Išspręskime šią nelygybę intervalo metodu, įvertindami kairę pusę. Norėdami tai padaryti, randame visos kvadratinės lygties šaknis:

6m 2 -5m+1=0. Diskriminantas D=b 2 -4ac=5 2 -4∙6∙1=25-24=1. Tada gauname y 1 ir y 2:

24. Tiesiosios prizmės pagrindu yra taisyklingas trikampis, kurio plotas yra Apskaičiuokite prizmės šoninio paviršiaus plotą, jei jos tūris yra 300 cm 3.

Duokime taisyklingąją trikampę prizmę ABCA 1 B 1 C 1, kurios pagrindu yra teisinga Δ ABC, jos plotas mums žinomas. Naudodami lygiakraščio trikampio ploto formulę randame savo trikampio ABC kraštinę. Kadangi tiesios prizmės tūris apskaičiuojamas pagal formulę V=S pagrindinis. ∙ H, ir mes taip pat žinome, tada galime rasti H - prizmės aukštį. Prizmės šoninis kraštas bus lygus prizmės aukščiui: AA 1 =H. Žinodami pagrindo kraštinę ir prizmės šoninio krašto ilgį, galite rasti jos šoninio paviršiaus plotą pagal formulę: S pusė. =P pagrindinis ∙ H.

25. Mokyklos viktorinoje buvo 20 klausimų. Už kiekvieną teisingą atsakymą dalyviui buvo skirta 12 taškų, o už kiekvieną neteisingą atsakymą – 10 taškų. Kiek teisingų atsakymų pateikė vienas iš dalyvių, jei atsakė į visus klausimus ir surinko 86 taškus?

Leiskite dalyviui pateikti x teisingų atsakymų. Tada jis turi (20) neteisingų atsakymų. Žinodami, kad už kiekvieną teisingą atsakymą jam buvo skirta 12 balų, o už kiekvieną neteisingą atimama po 10 balų ir tuo pačiu surinko 86 taškus, sudarysime lygtį:

12x-10·(20s)=86;

12x-200+10x=86;

22x=286 ⇒ x=286:22 ⇒ x=13. Dalyvis pateikė 13 teisingų atsakymų.

Linkiu jums pateikti 25 teisingus UNT matematikos testo atsakymus!

24. Taisyklingoje keturkampėje piramidėje aukštis lygus 3, šoninė briauna – 6. Raskite apie piramidę apibrėžtos rutulio spindulį.

Aplink taisyklingą piramidę MABCD, kurios aukštis MO=3, o šoninė briauna MA=6, aprašome rutulį, kurio centras yra taške O 1 ir spindulys MO 1. Būtina rasti rutulio spindulį MO 1. Apsvarstykite ΔMAM 1, kuriame kraštinė MM 1 yra rutulio skersmuo. Tada ∠MAM 1 =90°. Raskime hipotenuzą MM 1, jei žinoma kraštinė MA ir šios pusės MO projekcija į hipotenuzą. Prisiminti? Aukštis nubrėžtas iš viršūnės stačiu kampu prie hipotenuzos yra vidurkis proporcinga vertė tarp kojų projekcijų į hipotenuzę, o kiekviena koja yra vidutinė proporcinga reikšmė tarp visos hipotenuzės ir šios kojos projekcijos į hipotenuzą.Šioje užduotyje mums bus naudinga tik pabraukta taisyklės dalis.

Rašome lygybę: MA 2 =MO∙MM 1. Mes pakeičiame savo duomenis: 6 2 =3∙MM 1. Vadinasi, MM 1 =36:3=12. Mes nustatėme rutulio skersmenį, todėl spindulys MO 1 =6.

25. Petja yra vyresnė už Kolją, kuri yra vyresnė už Mišą, Maša yra vyresnė už Kolją, o Daša yra jaunesnė už Petiją, bet vyresnė už Mašą. Kas yra trečias pagal amžių?

Tarkime: senesnis reiškia daugiau. Petya yra vyresnė už Koliją, kuri yra vyresnė už Mišą Parašykime taip: Petya>Kolya>Misha. Daša yra jaunesnė už Petiją, bet vyresnė už Mašą parašykime taip: Maša<Даша<Петя, что будет равнозначно записи: Петя>Daša> Maša. Nes Maša vyresnė už Koliją, tada gauname: Petya>Dasha>Masha>Kolya. Ir galiausiai: Petya>Dasha>Masha>Kolya>Misha. Taigi, trečia pagal senumą yra Maša.

Linkiu sėkmingo pasiruošimo UNT!