Dönüşümleri kullanarak karmaşık bir fonksiyonun grafiklerini çizmek. Grafikleri dönüştürme
Hipotez: Bir fonksiyon denkleminin oluşumu sırasında grafiğin hareketini incelerseniz, tüm grafiklerin buna uyduğunu fark edeceksiniz. genel desenler bu nedenle formüle edebiliriz genel kanunlar fonksiyonlar ne olursa olsun, bu sadece çeşitli fonksiyonların grafiklerinin oluşturulmasını kolaylaştırmakla kalmayacak, aynı zamanda bunları problem çözmede de kullanacaktır.
Amaç: Fonksiyon grafiklerinin hareketini incelemek:
1) Görev edebiyat okumaktır
2) Çeşitli fonksiyonların grafiklerini oluşturmayı öğrenin
3) Doğrusal fonksiyonların grafiklerini dönüştürmeyi öğrenin
4) Problemleri çözerken grafik kullanma konusunu düşünün
Çalışmanın amacı: Fonksiyon grafikleri
Araştırma konusu: Fonksiyon grafiklerinin hareketleri
Uygunluk: Fonksiyonların grafiklerini oluşturmak, kural olarak, çok zaman alır ve öğrencinin dikkatini gerektirir, ancak fonksiyonların grafiklerini ve temel fonksiyonların grafiklerini dönüştürme kurallarını bilerek, fonksiyonların grafiklerini hızlı ve kolay bir şekilde oluşturabilirsiniz. Bu, yalnızca fonksiyon grafikleri oluşturma görevlerini tamamlamanıza değil, aynı zamanda bununla ilgili sorunları da çözmenize (maksimum (minimum zaman yüksekliği ve buluşma noktası) bulmak için) olanak tanır.
Bu proje okuldaki tüm öğrenciler için faydalıdır.
Literatür incelemesi:
Literatürde çeşitli fonksiyonların grafiklerini oluşturma yöntemlerinin yanı sıra bu fonksiyonların grafiklerini dönüştürme örnekleri tartışılmaktadır. Hemen hemen tüm temel fonksiyonların grafikleri çeşitli şekillerde kullanılmaktadır. teknik süreçler süreci daha net hayal etmenize ve sonucu programlamanıza olanak tanır
Kalıcı işlev. Bu fonksiyon y = b formülüyle verilir; burada b belirli bir sayıdır. Sabit bir fonksiyonun grafiği apsise paralel olan ve ordinat üzerindeki (0; b) noktasından geçen düz bir çizgidir. y = 0 fonksiyonunun grafiği x eksenidir.
Fonksiyon türleri 1Doğru orantılılık. Bu fonksiyon y = kx formülüyle verilir; burada orantı katsayısı k ≠ 0'dır. Doğru orantılılık grafiği orijinden geçen düz bir çizgidir.
Doğrusal fonksiyon. Böyle bir fonksiyon y = kx + b formülüyle verilir; burada k ve b gerçek sayılar. Doğrusal bir fonksiyonun grafiği düz bir çizgidir.
Doğrusal fonksiyonların grafikleri kesişebilir veya paralel olabilir.
Böylece, y = k 1 x + b 1 ve y = k 2 x + b 2 doğrusal fonksiyonlarının grafiklerinin çizgileri, k 1 ≠ k 2 ise kesişir; k 1 = k 2 ise çizgiler paraleldir.
2Ters orantı, k ≠ 0 olmak üzere y = k/x formülüyle verilen bir fonksiyondur. K'ya katsayı denir ters orantı. Ters orantı grafiği bir hiperboldür.
y = x 2 fonksiyonu parabol adı verilen bir grafikle temsil edilir: [-~; 0] fonksiyon azalır, fonksiyon arttığı aralıkta.
y = x 3 fonksiyonu tüm sayı doğrusu boyunca artar ve grafiksel olarak kübik bir parabol ile temsil edilir.
Doğal üslü kuvvet fonksiyonu. Bu fonksiyon y = x n formülüyle verilir; burada n, doğal sayı. Grafikler güç fonksiyonu doğal üslü n'ye bağlıdır. Örneğin, eğer n = 1 ise grafik düz bir çizgi olacaktır (y = x), eğer n = 2 ise grafik bir parabol olacaktır, vb.
Negatif tamsayı üssü olan bir kuvvet fonksiyonu y = x -n formülüyle temsil edilir; burada n bir doğal sayıdır. Bu fonksiyon tüm x ≠ 0 için tanımlanmıştır. Fonksiyonun grafiği aynı zamanda n üssüne de bağlıdır.
Pozitif kesirli üslü kuvvet fonksiyonu. Bu fonksiyon y = x r formülüyle temsil edilir; burada r pozitif indirgenemez bir kesirdir. Bu fonksiyon aynı zamanda ne çift ne de tektir.
Koordinat düzleminde bağımlı ve bağımsız değişkenler arasındaki ilişkiyi gösteren çizgi grafiği. Grafik bu öğeleri görsel olarak göstermeye yarar
Bağımsız değişken, fonksiyon tanımı alanında herhangi bir değeri alabilen bir değişkendir (burada verilen fonksiyon bir anlam taşır (sıfıra bölünemez))
İhtiyacınız olan fonksiyonların bir grafiğini oluşturmak için
1) VA'yı (kabul edilebilir değerler aralığı) bulun
2) bağımsız değişken için birkaç keyfi değer alın
3) Bağımlı değişkenin değerini bulun
4)İnşa koordinat uçağıüzerinde bu noktaları işaretleyin
5) Gerekirse çizgilerini bağlayın, ortaya çıkan grafiği inceleyin. Grafiklerin dönüşümü temel işlevler.
Grafikleri dönüştürme
Saf haliyle, temel temel işlevler ne yazık ki o kadar yaygın değildir. Sabitleri ve katsayıları ekleyerek temel temel fonksiyonlardan elde edilen temel fonksiyonlarla çok daha sık uğraşmanız gerekir. Bu tür fonksiyonların grafikleri, ilgili temel temel fonksiyonların grafiklerine geometrik dönüşümler uygulanarak (veya yeni bir koordinat sistemine geçilerek) oluşturulabilir. Örneğin, ikinci dereceden fonksiyon formül şu ikinci dereceden parabol ordinat eksenine göre üç kez sıkıştırılmış, apsis eksenine göre simetrik olarak görüntülenen, bu eksenin yönüne karşı 2/3 birim kaydırılan ve ordinat ekseni boyunca 2 birim kaydırılmış bir formül.
Bir fonksiyonun grafiğindeki bu geometrik dönüşümleri belirli örnekler kullanarak adım adım anlayalım.
f(x) fonksiyonunun grafiğinin geometrik dönüşümleri kullanılarak, aşağıdaki formüle ait herhangi bir fonksiyonun grafiği oluşturulabilir; burada formül, sırasıyla oy ve öküz eksenleri boyunca sıkıştırma veya germe katsayıları ve öndeki eksi işaretleridir. Formül ve formül katsayıları grafiğin koordinat eksenlerine göre simetrik bir görüntüsünü belirtir, a ve b sırasıyla apsis ve ordinat eksenlerine göre kaymayı belirler.
Dolayısıyla bir fonksiyonun grafiğinin üç tür geometrik dönüşümü vardır:
Birinci tip, apsis ve ordinat eksenleri boyunca ölçeklendirmedir (sıkıştırma veya uzatma).
Ölçeklendirme ihtiyacı birden farklı formül katsayılarıyla gösterilir; sayı 1'den küçükse grafik oy'a göre sıkıştırılır ve sayı 1'den büyükse ordinat ekseni boyunca uzatılır; ve apsis ekseni boyunca sıkıştırın.
İkinci tip, koordinat eksenlerine göre simetrik (ayna) bir ekrandır.
Bu dönüşümün gerekliliği formülün (bu durumda grafiği öküz eksenine göre simetrik olarak gösteriyoruz) ve formülün (bu durumda grafiği oy eksenine göre simetrik olarak gösteriyoruz) katsayılarının önündeki eksi işaretleri ile belirtilmektedir. eksen). Eksi işareti yoksa bu adım atlanır.








 İleri geri
İleri geri
Dikkat! Slayt önizlemeleri yalnızca bilgilendirme amaçlıdır ve sunumun tüm özelliklerini temsil etmeyebilir. Eğer ilgini çektiyse bu iş lütfen tam sürümünü indirin.
Dersin amacı: Fonksiyon grafiklerinin dönüşüm kalıplarını belirleyin.
Görevler:
Eğitici:
- Öğrencilere, belirli bir fonksiyonun grafiğini paralel çeviri, sıkıştırma (uzatma) kullanarak dönüştürerek fonksiyonların grafiklerini oluşturmayı öğretin. Farklı türde simetri.
Eğitici:
- Öğrencilerin kişisel niteliklerini (dinleme yeteneği), başkalarına karşı iyi niyeti, dikkatliliği, doğruluğu, disiplini ve grup halinde çalışma yeteneğini geliştirmek.
- Konuya olan ilgiyi ve bilgi edinme ihtiyacını geliştirin.
Gelişimsel:
- Mekansal hayal gücünü geliştirin ve mantıksal düşünmeöğrenciler, ortamda hızlı bir şekilde gezinme yeteneği; zekayı, becerikliliği geliştirin ve hafızayı eğitin.
Teçhizat:
- Multimedya kurulumu: bilgisayar, projektör.
Edebiyat:
- Bashmakov, M. I. Matematik [Metin]: başlayan kurumlar için ders kitabı. ve Çarşamba prof. eğitim / M.I. - 5. baskı, revize edildi. – M.: Yayın Merkezi “Akademi”, 2012. – 256 s.
- Bashmakov, M. I. Matematik. Sorun kitabı [Metin]: ders kitabı.
eğitim ödeneği kurumlar erken ve Çarşamba
- prof. eğitim / M. I. Bashmakov – M .: Yayın Merkezi “Akademi”, 2012. – 416 s.
- Ders planı:
- Organizasyon anı (3 dk).
- Bilgiyi güncelleme (7 dk).
- Yeni materyalin açıklanması (20 dk).
- Yeni malzemenin konsolidasyonu (10 dakika). Ders özeti (3 dk).
Ev ödevi
(2 dakika).
Dersler sırasında
1. Org. an (3 dakika).
Mevcut olanları kontrol ediyorum.
Dersin amacını anlatın.
Değişken büyüklükler arasındaki bağımlılıklar olarak fonksiyonların temel özellikleri, bu büyüklükleri ölçme yöntemini değiştirirken, yani ölçüm ölçeğini ve referans noktasını değiştirirken önemli ölçüde değişmemelidir. Bununla birlikte, değişken büyüklükleri ölçme yönteminin daha rasyonel bir şekilde seçilmesi nedeniyle, genellikle aralarındaki ilişkinin kaydedilmesini basitleştirmek ve bu kaydı standart bir forma getirmek mümkündür. Geometrik dilde, niceliklerin ölçülme biçimini değiştirmek, bugün üzerinde çalışacağımız bazı basit grafik dönüşümleri anlamına gelir.
2. Bilgiyi güncellemek (7 dk).
Grafik dönüşümlerinden bahsetmeden önce ele aldığımız materyali gözden geçirelim.
Sözlü çalışma. (Slayt 2). , , , .
Verilen işlevler:
3. Fonksiyonların grafiklerini açıklayın: 3. Yeni materyalin açıklanması (20 dk). Grafiklerin en basit dönüşümleri paralel aktarımı, sıkıştırılması (uzatılması) ve bazı simetri türleridir. Bazı dönüşümler tabloda sunulmaktadır
(Ek 1)
, (Slayt 3).
| Gruplarla çalışmak. | Her grup verilen fonksiyonların grafiklerini oluşturur ve sonucu tartışmaya sunar. | Fonksiyon örnekleri | Slayt |
| kuruluş birimi Açık A birimler yukarı eğer A>0 ve |A| eğer birimler aşağı A<0. | , | (Slayt 4)
|
|
| Eksen boyunca paralel transfer Ah Açık A sağa doğru ise birimler A>0 ve devamında - A birim sola eğer A<0. | , | (Slayt 5)
|
Fiziksel süreçlerin koşullarına bağlı olarak bazı büyüklükler sabit değerler alır ve sabit olarak adlandırılır, bazıları ise belirli koşullar altında değişir ve değişken olarak adlandırılır.
Çevrenin dikkatli bir şekilde incelenmesi, fiziksel niceliklerin birbirine bağlı olduğunu, yani bazı niceliklerdeki değişimin diğerlerinde de değişikliğe yol açtığını gösterir.
Matematiksel analiz, belirli fiziksel anlamdan soyutlanarak, karşılıklı olarak değişen nicelikler arasındaki niceliksel ilişkilerin incelenmesiyle ilgilenir. Matematiksel analizin temel kavramlarından biri fonksiyon kavramıdır.
Kümenin elemanlarını ve kümenin elemanlarını düşünün  (Şekil 3.1).
(Şekil 3.1).

Kümelerin elemanları arasında bir yazışma kurulursa  Ve
Ve  bir kural şeklinde
bir kural şeklinde  sonra fonksiyonun tanımlandığını not ederler
sonra fonksiyonun tanımlandığını not ederler  .
.
Tanım
3.1.
Yazışma  her bir öğeyle ilişkilendirilen
her bir öğeyle ilişkilendirilen  boş küme değil
boş küme değil  iyi tanımlanmış bazı unsurlar
iyi tanımlanmış bazı unsurlar  boş küme değil
boş küme değil  buna işlev veya eşleme adı verilir
buna işlev veya eşleme adı verilir  V
V  .
.
Sembolik olarak göster  V
V  şu şekilde yazılmıştır:
şu şekilde yazılmıştır:
 .
.
Aynı zamanda birçok  fonksiyonun tanım bölgesi denir ve gösterilir
fonksiyonun tanım bölgesi denir ve gösterilir  .
.
Buna karşılık birçok  fonksiyonun değer aralığı denir ve gösterilir
fonksiyonun değer aralığı denir ve gösterilir  .
.
Ayrıca şunu da belirtmek gerekir ki setin elemanları  bağımsız değişkenler olarak adlandırılır, kümenin elemanları
bağımsız değişkenler olarak adlandırılır, kümenin elemanları  bağımlı değişkenler denir.
bağımlı değişkenler denir.
Bir işlevi belirtme yöntemleri
Fonksiyon aşağıdaki ana yollarla belirtilebilir: tablo şeklinde, grafiksel, analitik.
Deneysel verilere dayanarak, işlevin değerlerini ve karşılık gelen bağımsız değişken değerlerini içeren tablolar derlenirse, işlevi belirtmenin bu yöntemine tablo şeklinde denir.
Aynı zamanda deney sonucunun bazı çalışmaları bir kayıt cihazında (osiloskop, kayıt cihazı vb.) görüntüleniyorsa, fonksiyonun grafiksel olarak belirtildiği not edilir.
En yaygın olanı, bir fonksiyonu belirlemenin analitik yoludur; bağımsız ve bağımlı değişkenlerin bir formül kullanılarak bağlandığı bir yöntem. Bu durumda fonksiyonun tanım alanı önemli bir rol oynar:
aynı analitik ilişkilerle verilmiş olmalarına rağmen farklıdırlar.
Yalnızca fonksiyon formülünü belirtirseniz  , o zaman bu fonksiyonun tanım alanının değişkenin bu değerlerinin kümesiyle örtüştüğünü düşünüyoruz.
, o zaman bu fonksiyonun tanım alanının değişkenin bu değerlerinin kümesiyle örtüştüğünü düşünüyoruz.  , bunun için ifade
, bunun için ifade  anlamı vardır. Bu bağlamda, bir fonksiyonun tanım kümesini bulma problemi özel bir rol oynamaktadır.
anlamı vardır. Bu bağlamda, bir fonksiyonun tanım kümesini bulma problemi özel bir rol oynamaktadır.
Görev 3.1. Bir fonksiyonun tanım kümesini bulun

Çözüm
İlk terim gerçek değerleri aldığında  ve ikincisi de. Dolayısıyla, belirli bir fonksiyonun tanım alanını bulmak için eşitsizlik sistemini çözmek gerekir:
ve ikincisi de. Dolayısıyla, belirli bir fonksiyonun tanım alanını bulmak için eşitsizlik sistemini çözmek gerekir:

Sonuç olarak böyle bir sistemin çözümü . Bu nedenle, fonksiyonun tanım alanı segmenttir.  .
.
Fonksiyon grafiklerinin en basit dönüşümleri
Temel temel fonksiyonların iyi bilinen grafiklerini kullanırsanız, fonksiyon grafiklerinin yapısı önemli ölçüde basitleştirilebilir. Aşağıdaki işlevlere ana temel işlevler adı verilir:
1) güç fonksiyonu  Nerede
Nerede  ;
;
2)üstel fonksiyon Nerede
Nerede 
 Ve
Ve  ;
;
3) logaritmik fonksiyon  , Nerede
, Nerede  - bir dışında herhangi bir pozitif sayı:
- bir dışında herhangi bir pozitif sayı:  Ve
Ve  ;
;
4) trigonometrik fonksiyonlar 



 ;
;
 .
.
5) ters trigonometrik fonksiyonlar  ;
; ;
;
 ;
;
 .
.
Temel fonksiyonlar, dört aritmetik işlem ve sonlu sayıda uygulanan süperpozisyonlar kullanılarak temel temel fonksiyonlardan elde edilen fonksiyonlardır.
Basit geometrik dönüşümler aynı zamanda bir fonksiyon grafiği oluşturma sürecini basitleştirmeyi de mümkün kılar. Bu dönüşümler aşağıdaki ifadelere dayanmaktadır:
y=f(x+a) fonksiyonunun grafiği, kaydırılmış (a >0 için sola, a için) y=f(x) grafiğidir.< 0 вправо) на |a| единиц параллельно осиOx.
y=f(x) +b fonksiyonunun grafiği, y=f(x)'in kaydırılmış grafiğidir (b>0'da yukarı, b'de)< 0 вниз) на |b| единиц параллельно осиOy.
y = mf(x) (m0) fonksiyonunun grafiği, y = f(x) m kez uzatılmış (m>1'de) veya sıkıştırılmış (0'da) grafiğidir. y = f(kx) fonksiyonunun grafiği, y = f(x) grafiğidir, k kez sıkıştırılmış (k >1 için) veya uzatılmış (0 için)< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx)
есть зеркальное отображение графика
y = f(–kx) от оси Oy.
Dönüşüm olmadan saf formdaki temel temel fonksiyonlar nadirdir, bu nedenle çoğu zaman ana fonksiyonlardan sabitler ve katsayılar eklenerek elde edilen temel fonksiyonlarla çalışmak zorunda kalırsınız. Bu tür grafikler, verilen temel fonksiyonların geometrik dönüşümleri kullanılarak oluşturulur.
Grafiği y = x 2 parabolü olan, Oy'ya göre üç kez sıkıştırılmış ve göre simetrik olan y = - 1 3 x + 2 3 2 + 2 formunda ikinci dereceden bir fonksiyon örneğini ele alalım. Ox'a doğru ve Ox boyunca 2 3 sağa, Oy boyunca 2 birim yukarı kaydırıldı. Koordinat çizgisi üzerinde şöyle görünür:
Yandex.RTB R-A-339285-1
Bir fonksiyonun grafiğinin geometrik dönüşümleri
Belirli bir grafiğin geometrik dönüşümlerini uygulayarak, k 1 > 0, k 2 > 0 olduğunda grafiğin ± k 1 · f (± k 2 · (x + a)) + b formundaki bir fonksiyonla tasvir edildiğini elde ederiz. 0'daki sıkıştırma katsayılarıdır< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1, O y ve O x boyunca. K 1 ve k 2 katsayılarının önündeki işaret, grafiğin eksenlere göre simetrik bir görüntüsünü gösterir, a ve b onu O x boyunca ve O y boyunca kaydırır.
Tanım 1
3 tip var grafiğin geometrik dönüşümleri:
- Ölçeklendirme O x ve O y boyunca. Bu, 0 olduğunda 1'e eşit olmadıkları sürece k 1 ve k 2 katsayılarından etkilenir.< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1 ise grafik O y boyunca uzatılır ve O x boyunca sıkıştırılır.
- Koordinat eksenlerine göre simetrik ekran. k 1'in önünde “-” işareti varsa simetri O x'e göre, k 2'nin önünde ise O y'ye göredir. “-” eksikse çözüm sırasında madde atlanır;
- Paralel aktarım (kaydırma) O x ve O y boyunca. Dönüşüm, a ve b katsayılarının 0'a eşit olmaması durumunda gerçekleştirilir. a pozitifse grafik | ile sola kaydırılır. bir | birimler, eğer a negatifse, o zaman aynı mesafede sağa doğru. B değeri, O y ekseni boyunca hareketi belirler; bu, b pozitif olduğunda fonksiyonun yukarı doğru hareket ettiği, b negatif olduğunda ise aşağı doğru hareket ettiği anlamına gelir.
Bir güç fonksiyonuyla başlayarak örnekler kullanarak çözümlere bakalım.
örnek 1
y = x 2 3'ü dönüştürün ve y = - 1 2 · 8 x - 4 2 3 + 3 fonksiyonunun grafiğini çizin.
Çözüm
Fonksiyonları şu şekilde temsil edelim:
y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3
k 1 = 2 olduğunda “-”, a = - 1 2, b = 3'ün varlığına dikkat etmekte fayda var. Buradan geometrik dönüşümlerin O y boyunca iki kez uzatılarak gerçekleştirildiğini, O x'e göre simetrik olarak gösterildiğini, sağa 1 2 ve yukarıya 3 birim kaydırıldığını anlıyoruz.
Orijinal güç fonksiyonunu tasvir edersek şunu elde ederiz:

boyunca iki kez gerildiğinde bunu elde ederiz

Ox'e göre simetrik olan haritalama şu şekildedir:

ve 1 2 sağa doğru ilerleyin

3 birim yukarıya doğru bir hareket şuna benziyor

Örnekleri kullanarak üstel fonksiyonların dönüşümlerine bakalım.
Örnek 2
y = - 1 2 1 2 (2 - x) + 8 üstel fonksiyonunun grafiğini oluşturun.
Çözüm.
Fonksiyonu bir kuvvet fonksiyonunun özelliklerine göre dönüştürelim. O zaman bunu anlıyoruz
y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8
Buradan y = 1 2 x dönüşüm zinciri elde ettiğimizi görebiliriz:
y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8
Orijinal üstel fonksiyonun şu forma sahip olduğunu bulduk:

Oy boyunca ikiye sıkıştırmak şunu verir

Ox boyunca uzanan
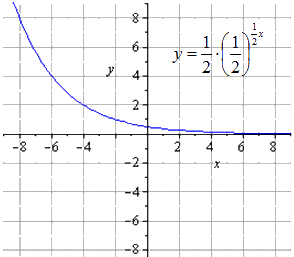
Ox'e göre simetrik haritalama

Eşleme O y'ye göre simetriktir

8 birim yukarı çık

Logaritmik fonksiyon y = ln (x) örneğini kullanarak çözümü ele alalım.
Örnek 3
y = ln e 2 · - 1 2 x 3 fonksiyonunu y = ln (x) dönüşümünü kullanarak oluşturun.
Çözüm
Çözmek için logaritmanın özelliklerini kullanmak gerekir, o zaman şunu elde ederiz:
y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2
Logaritmik bir fonksiyonun dönüşümleri şuna benzer:
y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2
Orijinal logaritmik fonksiyonun grafiğini çizelim

Sistemi O y'ye göre sıkıştırıyoruz

O x boyunca uzanıyoruz

O y'ye göre bir haritalama gerçekleştiriyoruz

2 birim yukarı kaydırıyoruz, şunu elde ediyoruz:

Grafikleri dönüştürmek için trigonometrik fonksiyon± k 1 · f (± k 2 · (x + a)) + b biçiminde bir çözüm şemasına uymak gerekir. k 2'nin T k 2'ye eşit olması gereklidir. Buradan şunu anlıyoruz: 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.
Y = sin x dönüşümüyle problem çözme örneklerine bakalım.
Örnek 4
y=sinx fonksiyonunun dönüşümlerini kullanarak y = - 3 sin 1 2 x - 3 2 - 2 grafiğini oluşturun.
Çözüm
Fonksiyonu ± k 1 · f ± k 2 · x + a + b biçimine indirmek gerekir. Bunun için:
y = - 3 günah 1 2 x - 3 2 - 2 = - 3 günah 1 2 (x - 3) - 2
k 1 = 3, k 2 = 1 2, a = - 3, b = - 2 olduğu görülmektedir. k 1'den önce bir "-" olduğu, ancak k 2'den önce olmadığı için, formun bir dönüşüm zincirini elde ederiz:
y = sin (x) → y = 3 günah (x) → y = 3 günah 1 2 x → y = - 3 günah 1 2 x → → y = - 3 günah 1 2 x - 3 → y = - 3 günah 1 2 (x - 3) - 2
Ayrıntılı sinüs dalgası dönüşümü. Orijinal sinüzoid y = sin (x) grafiğini çizerken, en küçük pozitif periyodun T = 2 π olarak kabul edildiğini görüyoruz. π 2 + 2 π · k noktalarında maksimumun bulunması; 1 ve minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

O y üç kat gerilir, bu da salınımların genliğindeki artışın 3 kat artacağı anlamına gelir. T = 2 π en küçük pozitif periyottur. Maksimumlar π 2 + 2 π · k'ye gider; 3, k ∈ Z, minimum - - π 2 + 2 π · k; - 3, k ∈ Z.
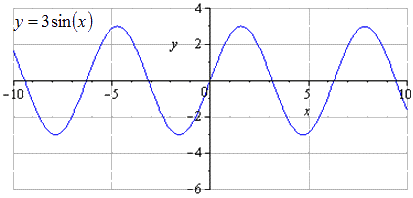
O x boyunca yarı yarıya gerildiğinde, en küçük pozitif periyodun 2 kat arttığını ve T = 2 π k 2 = 4 π'ye eşit olduğunu görüyoruz. Maksimumlar π + 4 π · k'ye gider; 3, k ∈ Z, minimumlar – in - π + 4 π · k; - 3, k ∈ Z.

Görüntü Ox'e göre simetrik olarak üretilir. En küçük pozitif dönem bu durumda değişmez ve T = 2 π k 2 = 4 π'ye eşittir. Maksimum geçiş şuna benzer: - π + 4 π · k; 3, k ∈ Z ve minimum π + 4 π · k'dir; - 3, k ∈ Z.
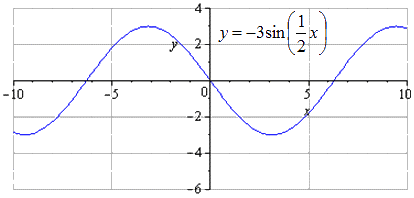
Grafik 2 birim aşağı kaydırılır. Asgari ortak süre değişmez. Noktalara geçişle maksimumları bulma - π + 3 + 4 π · k; 1, k ∈ Z, minimumlar - π + 3 + 4 π · k; - 5 , k ∈ Z .

Açık bu aşamada trigonometrik bir fonksiyonun grafiğinin dönüştürülmüş olduğu kabul edilir.
y = cos x fonksiyonunun ayrıntılı bir dönüşümünü ele alalım.
Örnek 5
y = cos x formundaki bir fonksiyon dönüşümünü kullanarak y = 3 2 cos 2 - 2 x + 1 fonksiyonunun bir grafiğini oluşturun.
Çözüm
Algoritmaya göre verilen fonksiyonun ± k 1 · f ± k 2 · x + a + b formuna indirgenmesi gerekmektedir. O zaman bunu anlıyoruz
y = 3 2 çünkü 2 - 2 x + 1 = 3 2 çünkü (- 2 (x - 1)) + 1
Koşuldan k 1 = 3 2, k 2 = 2, a = - 1, b = 1 olduğu, burada k 2'nin “-” olduğu ve k 1'den önce bulunmadığı açıktır.
Bundan, formun trigonometrik fonksiyonunun bir grafiğini elde ettiğimizi görüyoruz:
y = çünkü (x) → y = 3 2 çünkü (x) → y = 3 2 çünkü (2 x) → y = 3 2 çünkü (- 2 x) → → y = 3 2 çünkü (- 2 (x - 1) )) → y = 3 2 çünkü - 2 (x - 1) + 1
Grafiksel gösterimle adım adım kosinüs dönüşümü.
Y = cos (x) grafiği göz önüne alındığında, en kısa toplam periyodun T = 2 π olduğu açıktır. 2 π · k'de maksimumun bulunması; 1, k ∈ Z ve minimum π + 2 π · k; - 1, k ∈ Z.
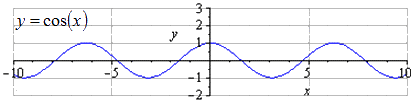
Oy boyunca 3 2 kat gerildiğinde salınımların genliği 3 2 kat artar. T = 2 π en küçük pozitif periyottur. 2 π · k'de maksimumun bulunması; 3 2, k ∈ Z, minimum π + 2 π · k; - 3 2 , k ∈ Z .

O x boyunca yarı yarıya sıkıştırıldığında, en küçük pozitif periyodun T = 2 π k 2 = π sayısı olduğunu buluruz. Maksimumlar π · k'ye aktarılır; 3 2 , k ∈ Z , minimumlar - π 2 + π · k ; - 3 2 , k ∈ Z .

Oy'a göre simetrik haritalama. Grafik tek olduğundan değişmeyecektir.

Grafik 1 kaydırıldığında. En küçük pozitif periyot T = π'de herhangi bir değişiklik yoktur. π · k + 1'de maksimumların bulunması; 3 2, k ∈ Z, minimumlar - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

1 kaydırıldığında en küçük pozitif periyot T = π'ye eşit olur ve değişmez. π · k + 1'de maksimumların bulunması; 5 2, k ∈ Z, minimum π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Kosinüs fonksiyonu dönüşümü tamamlandı.
y = t g x örneğini kullanarak dönüşümleri ele alalım.
Örnek 6
y = - 1 2 t g π 3 - 2 3 x + π 3 fonksiyonunun grafiğini, y = t g (x) fonksiyonunun dönüşümlerini kullanarak oluşturun.
Çözüm
Başlangıç olarak, verilen fonksiyonu ± k 1 · f ± k 2 · x + a + b biçimine indirgemek gerekir, bundan sonra şunu elde ederiz:
y = - 1 2 tg π 3 - 2 3 x + π 3 = - 1 2 tg - 2 3 x - π 2 + π 3
K 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3 olduğu ve k 1 ve k 2 katsayılarının önünde bir “-” olduğu açıkça görülmektedir. Bu, teğetsoitleri dönüştürdükten sonra elde ettiğimiz anlamına gelir.
y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3
Teğetlerin grafiksel gösterimle adım adım dönüştürülmesi.
Orijinal grafiğin y = t g(x) olduğunu biliyoruz. Pozitif dönemdeki değişim T = π'ye eşittir. Tanımın alanı - π 2 + π · k olarak kabul edilir; π 2 + π · k, k ∈ Z.
Oy boyunca 2 kez sıkıştırıyoruz. T = π, tanım alanının - π 2 + π · k biçiminde olduğu en küçük pozitif dönem olarak kabul edilir; π 2 + π · k, k ∈ Z.

O x 3 boyunca 2 kez gerin. En küçük pozitif periyodu hesaplayalım ve bu T = π k 2 = 3 2 π'ye eşitti. Ve fonksiyonun koordinatlarla tanım alanı 3 π 4 + 3 2 π · k'dir; 3 π 4 + 3 2 π · k, k ∈ Z, yalnızca tanımın alanı değişir.

Simetri Ox tarafındadır. Bu noktada dönem değişmeyecek.

Koordinat eksenlerini simetrik olarak görüntülemek gerekir. Bu durumda tanımın alanı değişmez. Program bir öncekiyle örtüşüyor. Bu, teğet fonksiyonunun tek olduğunu göstermektedir. Eğer Tek işlev O x ve O y'nin simetrik eşlemesini ayarlayın, ardından orijinal fonksiyona dönüştürün.

















