Ortalama seviye

Sağ üçgen. Tam Resimli Kılavuz (2019)

SAĞ ÜÇGEN. İLK SEVİYE.

Sorunlarda dik açı hiç gerekli değildir - sol alt, bu nedenle bu formdaki dik üçgeni tanımayı öğrenmeniz gerekir,

ve bunda

ve bunda

Dik üçgenin iyi yanı nedir? Şey... her şeyden önce, özel şeyler var güzel isimler onun tarafları için.

Çizime dikkat!

Unutmayın ve karıştırmayın: iki bacak var ve sadece bir hipotenüs var(bir ve tek, benzersiz ve en uzun)!

İsimleri tartıştık, şimdi en önemli şey: Pisagor Teoremi.

Pisagor teoremi.

Bu teorem dik üçgenle ilgili birçok problemin çözümünün anahtarıdır. Çok eski zamanlarda Pisagor tarafından kanıtlandı ve o zamandan beri bunu bilenlere pek çok fayda sağladı. Ve bunun en iyi yanı basit olmasıdır.

Bu yüzden, Pisagor teoremi:

Şakayı hatırlıyor musunuz: "Pisagor pantolonu her tarafta eşittir!"?

Aynı Pisagor pantolonunu çizelim ve onlara bakalım.

Bir çeşit şorta benzemiyor mu? Peki hangi taraflarda ve nerede eşitler? Şaka neden ve nereden geldi? Ve bu şaka tam olarak Pisagor teoremiyle veya daha kesin olarak Pisagor'un teoremini formüle etme şekliyle bağlantılıdır. Ve bunu şu şekilde formüle etti:

"Toplam karelerin alanları bacaklar üzerine inşa edilmiş, eşittir kare alan, hipotenüs üzerine inşa edilmiştir."

Gerçekten biraz farklı mı geliyor kulağa? Ve böylece Pisagor teoreminin ifadesini çizdiğinde ortaya çıkan resim tam olarak bu oldu.

Bu resimde küçük karelerin alanlarının toplamı büyük karenin alanına eşittir. Ve çocukların bacakların kareleri toplamının hipotenüsün karesine eşit olduğunu daha iyi hatırlaması için, esprili biri Pisagor pantolonuyla ilgili bu şakayı ortaya attı.

Neden şimdi Pisagor teoremini formüle ediyoruz?

Pisagor acı çekip karelerden mi bahsetti?

Görüyorsunuz, eski zamanlarda cebir diye bir şey yoktu! Herhangi bir işaret vs. yoktu. Hiçbir yazıt yoktu. Zavallı eski öğrencilerin her şeyi kelimelerle hatırlamasının ne kadar korkunç olduğunu hayal edebiliyor musunuz??! Ve Pisagor teoreminin basit bir formülasyonuna sahip olduğumuz için sevinebiliriz. Daha iyi hatırlamak için bir kez daha tekrarlayalım:

Artık kolay olmalı:

Hipotenüsün karesi bacakların karelerinin toplamına eşittir.

Dik üçgenlerle ilgili en önemli teorem tartışıldı. Bunun nasıl kanıtlandığıyla ilgileniyorsanız, aşağıdaki teori seviyelerini okuyun ve şimdi daha da ileri gidelim... trigonometrinin karanlık ormanına...! Korkunç kelimeler sinüs, kosinüs, teğet ve kotanjant.

Bir dik üçgende sinüs, kosinüs, teğet, kotanjant.

Aslında her şey o kadar da korkutucu değil. Elbette yazıda sinüs, kosinüs, tanjant ve kotanjantın “gerçek” tanımına da bakmak gerekir. Ama gerçekten istemiyorum, değil mi? Sevinebiliriz: Bir dik üçgenle ilgili problemleri çözmek için aşağıdaki basit şeyleri doldurmanız yeterlidir:

Neden her şey hemen köşede? Köşe nerede? Bunu anlayabilmek için 1'den 4'e kadar olan ifadelerin kelimelerle nasıl yazıldığını bilmeniz gerekir. Bakın, anlayın ve hatırlayın!

1.
Aslında kulağa şöyle geliyor:

Peki ya açı? Köşenin karşısında bir bacak var mı, yani karşıt (bir açı için) bacak var mı? Elbette var! Bu bir bacak!

Peki ya açı? Dikkatli bak. Hangi bacak köşeye bitişik? Tabii ki bacak. Bu, bacağın bitişik olduğu açı için ve

Şimdi dikkat edin! Bakın elimizde ne var:

Ne kadar havalı olduğunu görün:

Şimdi teğet ve kotanjanta geçelim.

Şimdi bunu kelimelerle nasıl yazabilirim? Açıya göre bacak nedir? Elbette karşısında - köşenin karşısında "yalan söylüyor". Peki ya bacak? Köşeye bitişik. Peki elimizde ne var?

Pay ve paydanın nasıl yer değiştirdiğini gördünüz mü?

Ve şimdi yine kornerler ve takas yapıldı:

Özet

Öğrendiğimiz her şeyi kısaca yazalım.

Pisagor teoremi:

Dik üçgenlerle ilgili ana teorem Pisagor teoremidir.

Pisagor teoremi

Bu arada, bacakların ve hipotenüsün ne olduğunu iyi hatırlıyor musun? Çok iyi değilse resme bakın - bilginizi tazeleyin

Pisagor teoremini birçok kez kullanmış olmanız oldukça olası, ancak böyle bir teoremin neden doğru olduğunu hiç merak ettiniz mi? Bunu nasıl kanıtlayabilirim? Antik Yunanlılar gibi yapalım. Kenarı olan bir kare çizelim.

Kenarlarını ne kadar akıllıca uzunluklara ayırdığımızı görün ve!

Şimdi işaretli noktaları birleştirelim

Ancak burada başka bir şeye dikkat çektik, ancak siz çizime bakıp bunun neden böyle olduğunu düşünüyorsunuz.

Büyük karenin alanı nedir? Sağ, . Daha küçük bir alana ne dersiniz? Kesinlikle, . Dört köşenin toplam alanı kalır. Bunları ikişer ikişer alıp hipotenüsleriyle birbirlerine yasladığımızı hayal edin. Ne oldu? İki dikdörtgen. Bu, "kesiklerin" alanının eşit olduğu anlamına gelir.

Şimdi hepsini bir araya getirelim.

Hadi dönüştürelim:

Böylece Pisagor'u ziyaret ettik; onun teoremini eski bir yöntemle kanıtladık.

Dik üçgen ve trigonometri

Bir dik üçgen için aşağıdaki ilişkiler geçerlidir:

Bir dar açının sinüsü, karşı kenarın hipotenüse oranına eşittir

Bir dar açının kosinüsü, komşu kenarın hipotenüse oranına eşittir.

Bir dar açının tanjantı karşı kenarın komşu kenara oranına eşittir.

Bir dar açının kotanjantı, komşu kenarın karşı kenara oranına eşittir.

Ve bir kez daha tüm bunlar bir tablet biçiminde:

Çok rahat!

Dik üçgenlerin eşitliğinin işaretleri

I. İki tarafta

II. Bacak ve hipotenüse göre

III. Hipotenüs ve dar açıya göre

IV. Bacak boyunca ve dar açı

A)

B)

Dikkat! Burada bacakların “uygun” olması çok önemlidir. Örneğin, eğer şu şekilde giderse:

O halde ÜÇGENLER EŞİT DEĞİLDİR aynı dar açıya sahip olmalarına rağmen.

Gerekiyor her iki üçgende de bacak bitişikti veya her ikisinde de zıttı.

Dik üçgenlerin eşitlik işaretlerinin, üçgenlerin eşitlik işaretlerinden ne kadar farklı olduğunu fark ettiniz mi? Konuya bir göz atın ve “sıradan” üçgenlerin eşitliği için elemanlarından üçünün eşit olması gerektiğine dikkat edin: iki kenar ve aralarındaki açı, iki açı ve aralarındaki kenar veya üç kenar. Ancak dik üçgenlerin eşitliği için yalnızca karşılık gelen iki öğe yeterlidir. Harika, değil mi?

Dik üçgenlerin benzerlik işaretleri ile durum yaklaşık olarak aynıdır.

Dik üçgenlerin benzerlik belirtileri

I. Dar bir açı boyunca

II. İki tarafta

III. Bacak ve hipotenüse göre

Dik üçgende medyan

Bu neden böyle?

Dik üçgen yerine tam bir dikdörtgen düşünün.

Bir köşegen çizelim ve bir nokta düşünelim; köşegenlerin kesişme noktası. Dikdörtgenin köşegenleri hakkında ne biliyorsunuz?

Peki bundan ne sonuç çıkıyor?

Böylece ortaya çıktı

1. - medyan:

Bu gerçeği unutmayın! Çok yardımcı oluyor!

Daha da şaşırtıcı olan ise bunun tam tersinin de geçerli olmasıdır.

Hipotenüse çizilen medyanın hipotenüsün yarısına eşit olmasından ne gibi bir fayda elde edilebilir? Hadi resme bakalım

Dikkatli bak. Elimizde: , yani noktadan üçgenin üç köşesine olan mesafelerin eşit olduğu ortaya çıktı. Ancak üçgende üçgenin üç köşesine de mesafeleri eşit olan tek bir nokta vardır ve bu da ÇEMBERİN MERKEZİdir. Peki ne oldu?

O halde şu "ayrıca..." ile başlayalım.

Şimdi ve'ye bakalım.

Ancak benzer üçgenlerin tüm açıları eşittir!

Aynı şey hakkında da söylenebilir ve

Şimdi birlikte çizelim:

Bu “üçlü” benzerlikten ne gibi faydalar elde edilebilir?

Mesela - Dik üçgenin yüksekliği için iki formül.

İlgili tarafların ilişkilerini yazalım:

Yüksekliği bulmak için orantıyı çözeriz ve şunu elde ederiz: ilk formül "Dik üçgende yükseklik":

O halde benzerliği uygulayalım: .

Ne olacak şimdi?

Yine orantıyı çözüyoruz ve ikinci formülü elde ediyoruz:

Bu formüllerin ikisini de çok iyi hatırlamanız ve size hangisi daha uygunsa onu kullanmanız gerekiyor. Tekrar yazalım

Pisagor teoremi:

Bir dik üçgende hipotenüsün karesi, dik kenarların karelerinin toplamına eşittir: .

Dik üçgenlerin eşitliğinin işaretleri:

• iki tarafta:
• bacak ve hipotenüse göre: veya
• bacak boyunca ve bitişik dar açı boyunca: veya
• bacak boyunca ve karşıt dar açıda: veya
• hipotenüs ve dar açıya göre: veya.

Dik üçgenlerin benzerlik işaretleri:

• bir akut köşe: veya
• iki bacağın orantılılığından:
• bacağın ve hipotenüsün orantılılığından: veya.

Bir dik üçgende sinüs, kosinüs, teğet, kotanjant

• Bir dik üçgenin dar açısının sinüsü, karşı tarafın hipotenüse oranıdır:
• Bir dik üçgenin dar açısının kosinüsü, bitişik kenarın hipotenüse oranıdır:
• Bir dik üçgenin dar açısının tanjantı, karşı tarafın bitişik kenara oranıdır:
• Bir dik üçgenin dar açısının kotanjantı, komşu kenarın karşı kenara oranıdır: .

Bir dik üçgenin yüksekliği: veya.

Bir dik üçgende tepe noktasından çizilen kenarortay dik açı, hipotenüsün yarısına eşittir: .

Dik üçgenin alanı:

• bacaklar yoluyla:

(Berlin Müzesi'nin 6619 numaralı papirüsüne göre). Cantor'a göre harpedonapteler veya "halat çekiciler" kenarları 3, 4 ve 5 olan dik üçgenleri kullanarak dik açılar inşa ettiler.

Yapım yöntemlerini çoğaltmak çok kolaydır. 12 m uzunluğunda bir ip alalım ve ona bir ucundan 3 m, diğer ucundan 4 metre uzaklıkta renkli bir şerit bağlayalım. Dik açı 3 ila 4 metre uzunluğunda kenarlar arasında olacaktır. Harpedonaptiyanlara, örneğin tüm marangozların kullandığı ahşap bir kare kullanıldığında, inşaat yöntemlerinin gereksiz hale geldiği yönünde itiraz edilebilir. Gerçekten de, böyle bir aletin bulunduğu Mısır çizimleri bilinmektedir, örneğin bir marangozluk atölyesini tasvir eden çizimler.

Babilliler arasında Pisagor teoremi hakkında biraz daha fazla şey biliniyor. Hammurabi dönemine, yani M.Ö. 2000 yılına kadar uzanan bir metinde. e. Bir dik üçgenin hipotenüsünün yaklaşık bir hesaplaması verilmiştir. Buradan Mezopotamya'da dik üçgenlerle hesaplamalar yapabildikleri sonucuna varabiliriz. en azından bazı durumlarda. Van der Waerden (Hollandalı bir matematikçi), bir yandan Mısır ve Babil matematiği hakkındaki mevcut bilgi düzeyine, diğer yandan da Yunan kaynaklarına ilişkin eleştirel bir çalışmaya dayanarak, yüksek bir olasılığın olduğu sonucuna vardı. Hipotenüsün karesi teoremi Hindistan'da M.Ö. 18. yüzyıldan beri biliniyordu. e.

MÖ 400 civarında. Proclus'a göre Platon, cebir ve geometriyi birleştirerek Pisagor üçlülerini bulmak için bir yöntem verdi. MÖ 300 civarında. e. Pisagor teoreminin en eski aksiyomatik kanıtı Öklid'in Elementlerinde ortaya çıktı.

Formülasyonlar

Geometrik formülasyon:

Teorem başlangıçta şu şekilde formüle edildi:

Cebirsel formülasyon:

Yani, üçgenin hipotenüsünün uzunluğunu , kenarlarının uzunluklarını ve ile gösteririz:

Teoremin her iki formülasyonu da eşdeğerdir, ancak ikinci formülasyon daha basittir; alan kavramını gerektirmez. Yani ikinci ifade, alan hakkında hiçbir şey bilmeden ve bir dik üçgenin yalnızca kenar uzunlukları ölçülerek doğrulanabilir.

Converse Pisagor teoremi:

Kanıt

Açık şu an Bu teoremin bilimsel literatürde 367 ispatı kaydedilmiştir. Muhtemelen Pisagor teoremi bu kadar etkileyici sayıda kanıta sahip olan tek teoremdir. Bu çeşitlilik ancak teoremin geometri açısından temel önemi ile açıklanabilir.

Elbette kavramsal olarak hepsi az sayıda sınıfa ayrılabilir. Bunlardan en ünlüsü: alan yöntemiyle ispatlar, aksiyomatik ve egzotik ispatlar (örneğin diferansiyel denklemler kullanılarak).

Benzer üçgenler sayesinde

Cebirsel formülasyonun aşağıdaki kanıtı, doğrudan aksiyomlardan oluşturulan kanıtların en basitidir. Özellikle şeklin alanı kavramını kullanmaz.

İzin vermek ABC dik açılı bir dik üçgen var C. Yüksekliği buradan çizelim C ve tabanını şu şekilde belirtin: H. Üçgen ACHüçgene benzer ABC iki köşede. Aynı şekilde üçgen CBH benzer ABC. Gösterimi tanıtarak

aldık

Eşdeğer nedir

Bunu topladığımızda şunu elde ederiz

kanıtlanması gereken şey buydu

Alan yöntemini kullanan ispatlar

Aşağıdaki ispatlar, görünürdeki basitliklerine rağmen, hiç de o kadar basit değil. Hepsi, ispatı Pisagor teoreminin ispatından daha karmaşık olan alan özelliklerini kullanır.

Eştamamlama yoluyla kanıt

1. Dört eşit sıralayalım dik üçgenŞekil 1'de gösterildiği gibi.
2. Kenarları olan dörtgen C ikisinin toplamı bir kare olduğundan keskin köşeler 90° ve açılma açısı 180°'dir.
3. Tüm şeklin alanı, bir yandan (a + b) kenarlı bir karenin alanına, diğer yandan dört üçgenin alanlarının toplamına eşittir. iç karenin alanı.

Q.E.D.

Öklid'in kanıtı

Öklid ispatının fikri şu şekildedir: Hipotenüs üzerine kurulan karenin alanının yarısının, bacaklar üzerine kurulan karelerin yarım alanlarının toplamına eşit olduğunu ve ardından hipotenüs üzerine inşa edilen karenin alanlarının toplamına eşit olduğunu kanıtlamaya çalışalım. büyük ve iki küçük kare eşittir.

Soldaki çizime bakalım. Üzerine bir dik üçgenin kenarlarına kareler inşa ettik ve C dik açısının tepesinden AB hipotenüsüne dik bir s ışını çizdik, hipotenüs üzerine inşa edilen ABIK karesini iki dikdörtgene böldü - BHJI ve HAKJ, sırasıyla. Bu dikdörtgenlerin alanlarının, karşılık gelen ayaklar üzerine inşa edilen karelerin alanlarına tam olarak eşit olduğu ortaya çıktı.

DECA karesinin alanının AHJK dikdörtgeninin alanına eşit olduğunu kanıtlamaya çalışalım.Bunu yapmak için yardımcı bir gözlem kullanacağız: Aynı yüksekliğe ve tabana sahip bir üçgenin alanı verilen dikdörtgen verilen dikdörtgenin alanının yarısına eşittir. Bu, bir üçgenin alanını taban ve yüksekliğin çarpımının yarısı olarak tanımlamanın bir sonucudur. Bu gözlemden, ACK üçgeninin alanının AHK üçgeninin alanına (şekilde gösterilmemiştir) eşit olduğu ve bunun da AHJK dikdörtgen alanının yarısına eşit olduğu anlaşılmaktadır.

Şimdi ACK üçgeninin alanının DECA karesinin alanının yarısına eşit olduğunu kanıtlayalım. Bunun için yapılması gereken tek şey ACK ve BDA üçgenlerinin eşitliğini ispatlamaktır (çünkü yukarıdaki özelliğe göre BDA üçgeninin alanı karenin alanının yarısına eşittir). Bu eşitlik açıktır: Üçgenlerin her iki tarafı ve aralarındaki açı eşittir. Yani - AB=AK, AD=AC - CAK ve BAD açılarının eşitliği hareket yöntemiyle kanıtlamak kolaydır: CAK üçgenini saat yönünün tersine 90° döndürürüz, o zaman iki üçgenin karşılık gelen kenarlarının soru çakışacaktır (karenin tepe noktasındaki açının 90° olması nedeniyle).

BCFG karesi ile BHJI dikdörtgeninin alanlarının eşitliğinin mantığı tamamen benzerdir.

Böylece hipotenüs üzerine kurulan bir karenin alanının, bacaklar üzerine kurulan karelerin alanlarından oluştuğunu kanıtladık. Bu kanıtın arkasındaki fikir yukarıdaki animasyonla daha da açıklanmaktadır.

Leonardo da Vinci'nin Kanıtı

İspatın ana unsurları simetri ve harekettir.

Çizimi ele alalım, simetriden görülebileceği gibi, parça kareyi iki özdeş parçaya böler (çünkü üçgenler yapı olarak eşittir).

Nokta etrafında saat yönünün tersine 90 derecelik bir dönüş kullanarak gölgeli şekillerin eşitliğini görüyoruz.

Artık gölgelendirdiğimiz şeklin alanının, küçük karelerin (bacaklar üzerine inşa edilmiş) alanlarının yarısı ile orijinal üçgenin alanının toplamına eşit olduğu açıktır. Öte yandan, hipotenüs üzerine inşa edilen büyük karenin alanının yarısı artı orijinal üçgenin alanına eşittir. Böylece küçük karelerin alanlarının toplamının yarısı büyük karenin alanının yarısına eşit olur ve dolayısıyla ayaklar üzerine kurulan karelerin alanlarının toplamı da üzerine kurulan karenin alanına eşit olur. hipotenüs.

Sonsuz küçük yöntemle kanıt

Diferansiyel denklemleri kullanan aşağıdaki ispat, genellikle 20. yüzyılın ilk yarısında yaşayan ünlü İngiliz matematikçi Hardy'ye atfedilir.

Şekilde gösterilen çizime bakıp taraftaki değişimi gözlemlemek A sonsuz küçük yan artışlar için aşağıdaki ilişkiyi yazabiliriz İle Ve A(üçgen benzerliğini kullanarak):

Değişkenlerin ayrılması yöntemini kullanarak şunu buluruz:

Her iki tarafta da artış olması durumunda hipotenüsteki değişimin daha genel bir ifadesi

Bu denklemin integralini alarak ve başlangıç ​​koşullarını kullanarak şunu elde ederiz:

Böylece istenilen cevaba ulaşıyoruz

Görülmesi kolay olduğu gibi, son formüldeki ikinci dereceden bağımlılık, üçgenin kenarları ve artışlar arasındaki doğrusal orantılılık nedeniyle ortaya çıkarken, toplam, farklı bacakların artışlarından gelen bağımsız katkılarla ilişkilendirilir.

Bacaklardan birinde (bu durumda bacak) bir artış yaşanmadığını varsayarsak daha basit bir kanıt elde edilebilir. Daha sonra entegrasyon sabiti için şunu elde ederiz:

Varyasyonlar ve genellemeler

Üç tarafta benzer geometrik şekiller

Benzer üçgenler için genelleme, yeşil şekillerin alanı A + B = mavi C'nin alanı

Benzer dik üçgenleri kullanan Pisagor teoremi

Öklid, Pisagor teoremini eserinde genelleştirdi Başlangıçlar, kenarlardaki karelerin alanlarını benzer geometrik şekillerin alanlarına genişleterek:

Bir dik üçgenin kenarlarına benzer geometrik şekiller (bkz. Öklid geometrisi) oluşturursak, iki küçük rakamın toplamı büyük rakamın alanına eşit olacaktır.

Bu genellemenin ana fikri, böyle bir geometrik şeklin alanının, herhangi bir doğrusal boyutunun karesiyle ve özellikle herhangi bir kenarın uzunluğunun karesiyle orantılı olmasıdır. Bu nedenle alanlarla benzer rakamlar için A, B Ve C uzunluklu kenarlar üzerine inşa edilmiştir A, B Ve C, sahibiz:

Ancak Pisagor teoremine göre, A 2 + B 2 = C 2 o zaman A + B = C.

Tam tersi, eğer bunu kanıtlayabilirsek A + B = C Pisagor teoremini kullanmadan benzer üç geometrik şekil için ters yönde hareket ederek teoremin kendisini kanıtlayabiliriz. Örneğin başlangıç ​​merkezi üçgeni üçgen olarak yeniden kullanılabilir. C hipotenüs ve iki benzer dik üçgen ( A Ve B), ortadaki üçgenin yüksekliğine bölünmesiyle oluşturulan diğer iki tarafa inşa edilmiştir. Bu durumda iki küçük üçgenin alanlarının toplamı açıkça üçüncünün alanına eşit olur, dolayısıyla A + B = C ve önceki ispatı yerine getirerek Ters sipariş Pisagor teoremini a 2 + b 2 = c 2 elde ederiz.

Kosinüs teoremi

Pisagor teoremi, keyfi bir üçgenin kenarlarının uzunluklarını ilişkilendiren daha genel kosinüs teoreminin özel bir durumudur:

burada θ kenarlar arasındaki açıdır A Ve B.

Eğer θ 90 derece ise o zaman çünkü θ = 0 ve formül olağan Pisagor teoremine göre basitleştirilir.

Serbest Üçgen

Kenarları olan keyfi bir üçgenin seçilen herhangi bir köşesine a, b, c bir ikizkenar üçgeni öyle yazın ki eşit açılar tabanındaki θ seçilen açıya eşitti. Seçilen θ açısının belirtilen tarafın karşısında bulunduğunu varsayalım. C. Sonuç olarak, kenarın karşısında bulunan θ açısına sahip ABD üçgeni elde ettik. A ve partiler R. İkinci üçgen, kenarın karşısında bulunan θ açısı tarafından oluşturulur. B ve partiler İle uzunluk S, resimde gösterildiği gibi. Sabit İbn Kurra bu üç üçgenin kenarlarının birbiriyle ilişkili olduğunu şu şekilde ileri sürmüştür:

θ açısı π/2'ye yaklaştıkça ikizkenar üçgenin tabanı küçülür ve r ve s kenarları giderek daha az örtüşür. θ = π/2 olduğunda ADB bir dik üçgen haline gelir, R + S = C ve başlangıç ​​Pisagor teoremini elde ederiz.

Argümanlardan birini ele alalım. ABC Üçgeni ABD üçgeniyle aynı açılara sahiptir ancak ters sıradadır. (İki üçgenin B köşesinde ortak bir açısı vardır, her ikisi de θ açısına sahiptir ve ayrıca üçgenin açılarının toplamına göre aynı üçüncü açıya sahiptir.) Buna göre ABC, DBA üçgeninin ABD yansımasına benzer, şu şekilde: alt şekilde gösterilmiştir. arasındaki ilişkiyi yazalım. zıt taraflar ve θ açısına bitişik,

Ayrıca başka bir üçgenin yansıması,

Kesirleri çarpalım ve şu iki oranı toplayalım:

Q.E.D.

Paralelkenarlar aracılığıyla keyfi üçgenler için genelleme

Keyfi üçgenler için genelleme,
yeşil alan arsa = alan mavi

Yukarıdaki şekildeki tezin kanıtı

Dik olmayan üçgenler için kare yerine üç kenarı paralelkenar kullanarak bir genelleme daha yapalım. (kareler özel bir durumdur.) Üstteki şekil, dar açılı bir üçgen için, uzun kenardaki paralelkenarın alanının, uzun kenardaki paralelkenarın diğer iki kenardaki paralelkenarların toplamına eşit olduğunu göstermektedir. kenar şekilde gösterildiği gibi yapılır (oklarla gösterilen boyutlar aynıdır ve alt paralelkenarın kenarlarını belirler). Karelerin paralelkenarlarla değiştirilmesi, MS 4'te İskenderiyeli Pappus tarafından formüle edildiği düşünülen ilk Pisagor teoremine açık bir benzerlik taşıyor. e.

Alttaki şekil ispatın ilerleyişini göstermektedir. Üçgenin sol tarafına bakalım. Soldaki yeşil paralelkenar mavi paralelkenarın sol tarafıyla aynı alana sahiptir çünkü tabanları aynıdır B ve yükseklik H. Ek olarak, sol yeşil paralelkenar üst resimdeki sol yeşil paralelkenarla aynı alana sahiptir çünkü ortak bir tabanı (üçgenin sol üst tarafı) ve üçgenin o tarafına dik ortak bir yüksekliği paylaşırlar. Üçgenin sağ tarafı için de benzer mantık yürüterek alttaki paralelkenarın iki yeşil paralelkenarla aynı alana sahip olduğunu kanıtlayacağız.

Karışık sayılar

Pisagor teoremi Kartezyen koordinat sisteminde iki nokta arasındaki mesafeyi bulmak için kullanılır ve bu teorem tüm gerçek koordinatlar için geçerlidir: mesafe S iki nokta arasında ( a, b) Ve ( CD) eşittir

Karmaşık sayılar gerçek bileşenli vektörler olarak ele alınırsa formülde herhangi bir sorun olmaz X + ben = (X, sen). . Örneğin mesafe S 0 + 1 arasında Ben ve 1 + 0 Ben vektörün modülü olarak hesaplanır (0, 1) − (1, 0) = (−1, 1), veya

Ancak karmaşık koordinatlara sahip vektörlerle yapılan işlemler için Pisagor formülünde bazı iyileştirmeler yapılması gerekmektedir. Karmaşık sayılarla noktalar arasındaki mesafe ( A, B) Ve ( C, D); A, B, C, Ve D tamamı karmaşık, mutlak değerleri kullanarak formüle ediyoruz. Mesafe S vektör farkına dayalı (A − C, B − D) aşağıdaki biçimde: fark olsun A − C = P+ben Q, Nerede P- farkın gerçek kısmı, Q sanal kısımdır ve i = √(−1). Aynı şekilde izin ver B − D = R+ben S. Daha sonra:

için karmaşık eşlenik sayı nerede? Örneğin noktalar arasındaki mesafe (A, B) = (0, 1) Ve (C, D) = (Ben, 0) farkı hesaplayalım (A − C, B − D) = (−Ben, 1) ve karmaşık eşlenikler kullanılmasaydı sonuç 0 olurdu. Bu nedenle, geliştirilmiş formülü kullanarak şunu elde ederiz:

Modül şu şekilde tanımlanır:

Stereometri

Üç boyutlu uzay için Pisagor teoreminin önemli bir genellemesi, adını J.-P.'den alan de Goy teoremidir. de Gois: Eğer bir tetrahedron dik açıya sahipse (bir küpte olduğu gibi), o zaman dik açının karşısındaki yüzün alanının karesi, diğer üç yüzün alanlarının karelerinin toplamına eşittir. Bu sonuç şu şekilde özetlenebilir: " N boyutlu Pisagor teoremi":

Üç boyutlu uzayda Pisagor teoremi AD köşegenini üç kenarla ilişkilendirir.

Başka bir genelleme: Pisagor teoremi stereometriye aşağıdaki biçimde uygulanabilir. Şekilde gösterildiği gibi dikdörtgen bir paralel yüzlü düşünün. Pisagor teoremini kullanarak BD köşegeninin uzunluğunu bulalım:

üç tarafın bir dik üçgen oluşturduğu yer. AD köşegeninin uzunluğunu bulmak için yatay BD köşegenini ve AB dikey kenarını kullanırız, bunun için yine Pisagor teoremini kullanırız:

veya her şeyi tek bir denklemde yazarsak:

Bu sonuç, vektörün büyüklüğünü belirlemek için kullanılan üç boyutlu bir ifadedir. v(çapraz AD), dik bileşenleri cinsinden ifade edilir ( v k ) (karşılıklı olarak üç dik kenar):

Bu denklem Pisagor teoreminin çok boyutlu uzay için bir genellemesi olarak düşünülebilir. Ancak sonuç aslında Pisagor teoreminin birbirini izleyen dik düzlemlerdeki dik üçgen dizisine tekrar tekrar uygulanmasından başka bir şey değildir.

Vektör Uzayı

Dik bir vektör sistemi durumunda, Pisagor teoremi olarak da adlandırılan bir eşitlik vardır:

Bunlar vektörün koordinat eksenlerine izdüşümü ise, o zaman bu formül Öklid mesafesiyle çakışır ve vektörün uzunluğunun, bileşenlerinin karelerinin toplamının kareköküne eşit olduğu anlamına gelir.

Bu eşitliğin sonsuz bir vektör sistemi durumundaki benzerine Parseval eşitliği denir.

Öklid dışı geometri

Pisagor teoremi Öklid geometrisinin aksiyomlarından türetilmiştir ve aslında yukarıda yazıldığı haliyle Öklid dışı geometri için geçerli değildir. (Yani Pisagor teoreminin, Öklid'in paralellik varsayımının bir nevi eşdeğeri olduğu ortaya çıkıyor.) Başka bir deyişle, Öklid dışı geometride bir üçgenin kenarları arasındaki ilişki zorunlu olarak Pisagor teoreminden farklı bir biçimde olacaktır. Örneğin, küresel geometride bir dik üçgenin her üç tarafı da (örneğin A, B Ve C Birim kürenin oktantını (sekizinci kısım) sınırlayan ), Pisagor teoremine aykırı olan π/2 uzunluğa sahiptir, çünkü A 2 + B 2 ≠ C 2 .

Burada Öklid dışı geometrinin iki durumunu ele alalım: küresel ve hiperbolik geometri; her iki durumda da, dik üçgenler için Öklid uzayına gelince, Pisagor teoreminin yerini alan sonuç kosinüs teoreminden çıkar.

Bununla birlikte, üçgenin dikdörtgen olması şartının yerine üçgenin iki açısının toplamının üçüncü açıya eşit olması koşulu getirilirse, Pisagor teoremi hiperbolik ve eliptik geometri için geçerliliğini korur. A+B = C. O zaman kenarlar arasındaki ilişki şuna benzer: çapları olan dairelerin alanlarının toplamı A Ve Bçapı olan bir dairenin alanına eşit C.

Küresel geometri

Yarıçaplı bir küre üzerindeki herhangi bir dik üçgen için R(örneğin, bir üçgendeki γ açısı dik ise) kenarlarla A, B, C Taraflar arasındaki ilişki şöyle görünecek:

Bu eşitlik, tüm küresel üçgenler için geçerli olan küresel kosinüs teoreminin özel bir durumu olarak türetilebilir:

burada cosh hiperbolik kosinüstür. Bu formül, tüm üçgenler için geçerli olan hiperbolik kosinüs teoreminin özel bir durumudur:

burada γ, tepe noktası kenara zıt olan açıdır C.

Nerede G ben metrik tensör denir. Konumun bir fonksiyonu olabilir. Bu tür eğrisel uzaylar Riemann geometrisini içerir: genel örnek. Bu formülasyon aynı zamanda eğrisel koordinatlar kullanıldığında Öklid uzayı için de uygundur. Örneğin kutupsal koordinatlar için:

Vektör çizimleri

Pisagor teoremi bir vektör çarpımının büyüklüğü için iki ifadeyi birbirine bağlar. Çapraz çarpımı tanımlamaya yönelik bir yaklaşım, bunun denklemi karşılamasını gerektirir:

Bu formül nokta çarpımını kullanır. Denklemin sağ tarafına Gram determinantı denir. A Ve B bu iki vektörün oluşturduğu paralelkenarın alanına eşittir. Bu gerekliliğin yanı sıra vektör çarpımının bileşenlerine dik olması şartına dayanarak A Ve B bundan, 0 ve 1 boyutlu uzaydaki önemsiz durumlar dışında, çapraz çarpımın yalnızca üç ve yedi boyutta tanımlandığı sonucu çıkar. Açının tanımını kullanıyoruz N boyutlu uzay:

Bir çapraz çarpımın bu özelliği, büyüklüğünü şu şekilde verir:

Pisagor'un temel trigonometrik özdeşliği sayesinde değerini yazmanın başka bir biçimini elde ederiz:

Çapraz çarpımı tanımlamaya alternatif bir yaklaşım, büyüklüğü için bir ifade kullanmaktır. Daha sonra ters sırayla akıl yürüterek skaler çarpımla bir bağlantı elde ederiz:

Ayrıca bakınız

Notlar

1. Tarih konusu: Babil matematiğinde Pisagor teoremi
2. ( , s. 351) s. 351
3. ( , Cilt I, s. 144)
4. Tartışma tarihsel gerçekler(, s. 351) s. 351'de verilmiştir
5. Kurt Von Fritz (Nisan 1945). " Keşif Metapontumlu Hippasus tarafından Ölçülmezlik". Matematik Yıllıkları, İkinci Seri(Matematik Yıllıkları) 46 (2): 242–264.
6. Lewis Carroll, “Düğümlü Hikaye”, M., Mir, 1985, s. 7
7. Asger Aaboe Matematiğin erken tarihinden bölümler. - Amerika Matematik Derneği, 1997. - S. 51. - ISBN 0883856131
8. Python Önerisi kaydeden Elisha Scott Loomis
9. Öklid'in Elementler: Kitap VI, Öneri VI 31: “Dik açılı üçgenlerde, dik açıyı gören taraftaki şekil, dik açıyı içeren kenarlardaki benzer ve benzer şekilde tanımlanan şekillere eşittir.”
10. Lawrence S. Leff alıntı yapılan çalışma. - Barron'un Eğitim Serisi - S. 326. - ISBN 0764128922
11. Howard Whitley Eves§4.8:...Pisagor teoreminin genelleştirilmesi // Matematikte büyük anlar (1650'den önce). - Amerika Matematik Derneği, 1983. - S. 41. - ISBN 0883853108
12. Tâbit ibn Qorra (tam adı Thābit ibn Kurra ibn Merwan Al-Ṣābiʾ al-Ḥarrānī) (MS 826-901), Öklid'in Elementleri ve diğer matematik konuları üzerine kapsamlı yazılar yazan, Bağdat'ta yaşayan bir doktordu.
13. Aydın Sayılı (Mart 1960). "Sâbit ibn Kurra'nın Pisagor Teoreminin Genelleştirilmesi." IŞİD 51 (1): 35–37. DOI:10.1086/348837.
14. Judith D.Sally, Paul Sally Alıştırma 2.10 (ii) // Atıf yapılan çalışma. - S. 62. - ISBN 0821844032
15. Böyle bir yapının ayrıntıları için bkz. George JenningsŞekil 1.32: Genelleştirilmiş Pisagor teoremi // Uygulamalı modern geometri: 150 rakamlı. - 3 üncü. - Springer, 1997. - S. 23. - ISBN 038794222X
16. Arlen Brown, Carl M. PearcyÖğe C: Keyfi norm N-tuple ... // Analize giriş. - Springer, 1995. - S. 124. - ISBN 0387943692 Ayrıca bkz. sayfa 47-50.
17. Alfred Gray, Elsa Abbena, Simon Salamon Mathematica ile eğrilerin ve yüzeylerin modern diferansiyel geometrisi. - 3 üncü. - CRC Press, 2006. - S. 194. - ISBN 1584884487
18. Rajendra Bhatia Matris analizi. - Springer, 1997. - S. 21. - ISBN 0387948465
19. Stephen W. Hawking alıntı yapılan çalışma. - 2005. - S. 4. - ISBN 0762419229
20. Eric W.Weisstein CRC kısa matematik ansiklopedisi. - 2.. - 2003. - S. 2147. - ISBN 1584883472
21. Alexander R.Pruss

GEOMETRİK ŞEKİLLERİN ALANININ ÖLÇÜLMESİ.

§ 58. Pisagor Teoremi 1.

__________
1 Pisagor, yaklaşık 2500 yıl önce (MÖ 564-473) yaşamış bir Yunan bilim adamıdır.
_________

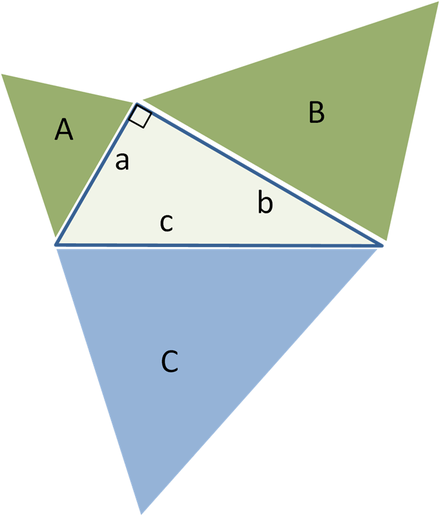
Bize kenarları eşit olan bir dik üçgen verilsin. A, B Ve İle(Çizim 267).

Yanlarına kareler oluşturalım. Bu karelerin alanları sırasıyla eşittir A 2 , B 2 ve İle 2. Hadi bunu kanıtlayalım İle 2 = bir 2 +b 2 .

İki kare MKOR ve M"K"O"R" (çizim 268, 269) oluşturalım, her birinin tarafı olarak ABC dik üçgeninin bacaklarının toplamına eşit bir parça alalım.

Bu karelerde 268 ve 269 numaralı çizimlerde gösterilen inşaatları tamamladıktan sonra MCOR meydanının alanları olan iki kareye bölündüğünü göreceğiz. A 2 ve B Her biri ABC dik üçgenine eşit olan 2 ve dört eşit dik üçgen. M"K"O"R" karesi bir dörtgene (çizim 269'da gölgelendirilmiştir) ve her biri ABC üçgenine eşit olan dört dik üçgene bölünmüştür. Gölgeli bir dörtgen, kenarları eşit olduğu için bir karedir (her biri ABC üçgeninin hipotenüsüne eşittir, yani. İle) ve açılar doğru / 1 + / 2 = 90°, buradan / 3 = 90°).

Böylece, bacaklar üzerine inşa edilen karelerin alanlarının toplamı (çizim 268'de bu kareler gölgelendirilmiştir), dört eşit üçgenin alanlarının toplamı olmadan MCOR karesinin alanına ve ​​hipotenüs üzerine inşa edilen kare (çizim 269'da bu kare de gölgelendirilmiştir) M"K"O"R" karesinin alanına eşittir, MCOR'un karesine eşittir, alanların toplamı olmadan dört benzer üçgen. Bu nedenle bir dik üçgenin hipotenüsü üzerine kurulan karenin alanı, bacaklar üzerine kurulan karelerin alanlarının toplamına eşittir.

Formülü alıyoruz İle 2 = bir 2 +b 2 nerede İle- hipotenüs, A Ve B- dik üçgenin bacakları.

Pisagor teoremi genellikle kısaca şu şekilde formüle edilir:

Bir dik üçgende hipotenüsün karesi dik kenarların karelerinin toplamına eşittir.

Formülden İle 2 = bir 2 +b 2 aşağıdaki formülleri alabilirsiniz:

A 2 = İle 2 - B 2 ;
B 2 = İle 2 - A 2 .

Bu formüller, bir dik üçgenin bilinmeyen kenarını verilen iki kenardan bulmak için kullanılabilir.
Örneğin:

a) eğer bacaklar verilirse A= 4cm, B=3 cm ise hipotenüsü bulabilirsiniz ( İle):
İle 2 = bir 2 +b 2, yani İle 2 = 4 2 + 3 2; 2 = 25 ile, dolayısıyla İle= √25 =5 (cm);

b) Hipotenüs verilirse İle= 17 cm ve bacak A= 8 cm, sonra başka bir bacak bulabilirsiniz ( B):

B 2 = İle 2 - A 2, yani B 2 = 17 2 - 8 2 ; B 2 = 225, buradan B= √225 = 15 (cm).

Sonuçlar: ABC ve A dik üçgenlerinin 1 B 1 C 1 hipotenüsü varsa İle Ve İle 1 eşittir ve bacak B ABC üçgeni bacaktan daha uzundur B 1 üçgen A 1 B 1 C 1,
sonra bacak A ABC üçgeni bacaktan daha küçüktür A 1 üçgen A 1 B 1 C 1. (Bu sonucu gösteren bir çizim yapın.)

Aslında Pisagor teoremine dayanarak şunu elde ederiz:

A 2 = İle 2 - B 2 ,
A 1 2 = İle 1 2 - B 1 2

Yazılı formüllerde eksilenler eşittir ve birinci formüldeki çıkan ikinci formüldeki çıkandan büyük olduğundan birinci fark ikinciden küçüktür,
yani. A 2 < A 12. Nerede A< A 1 .

Egzersizler.

1. Çizim 270'i kullanarak ikizkenar dik üçgen için Pisagor teoremini kanıtlayın.

2. Bir dik üçgenin bir kenarı 12 cm, diğeri 5 cm'dir Bu üçgenin hipotenüs uzunluğunu hesaplayınız.

3. Bir dik üçgenin hipotenüsü 10 cm, kenarlarından biri 8 cm'dir Bu üçgenin diğer kenarının uzunluğunu hesaplayınız.

4. Bir dik üçgenin hipotenüsü 37 cm, bir dik kenarı 35 cm'dir Bu üçgenin diğer bacağının uzunluğunu hesaplayınız.

5. Alanı verilen karenin iki katı büyüklüğünde bir kare oluşturun.

6. Alanı verilen karenin yarısı kadar olan bir kare oluşturun. Not. Bu kareye köşegenler çizin. Bu köşegenlerin yarısına kurulan kareler aradığımız kareler olacaktır.

7. Bir dik üçgenin kenarları sırasıyla 12 cm ve 15 cm'dir Bu üçgenin hipotenüs uzunluğunu 0,1 cm doğrulukla hesaplayın.

8. Bir dik üçgenin hipotenüsü 20 cm, bir kenarı 15 cm'dir, diğer kenarının uzunluğunu 0,1 cm'ye yakın hesaplayın.

9. Merdivenin alt ucunun binadan 2,5 m uzakta olması gerekiyorsa, 6 m yükseklikteki bir pencereye bağlanabilmesi için merdiven ne kadar uzun olmalıdır? (Grafik 271.)

1

Shapovalova L.A. (Egorlykskaya istasyonu, MBOU ESOSH No. 11)

1. Glazer G.I. Okul sınıflarında matematik tarihi VII - VIII, öğretmenler için el kitabı, - M: Prosveshchenie, 1982.

2. Dempan I.Ya., Vilenkin N.Ya. “Bir Matematik Ders Kitabının Sayfalarının Arkası” 5-6. sınıf öğrencileri için bir el kitabı. – M.: Eğitim, 1989.

3. Zenkevich I.G. "Matematik dersinin estetiği." – M.: Eğitim, 1981.

4. Litzman V. Pisagor Teoremi. – M., 1960.

5.Voloshinov A.V. "Pisagor". – M., 1993.

6. Pichurin L.F. "Bir cebir ders kitabının sayfalarının arkasında." – M., 1990.

7. Zemlyakov A.N. "10. sınıfta geometri." – M., 1986.

8. Gazete “Matematik” 17/1996.

9. Gazete “Matematik” 3/1997.

10. Antonov N.P., Vygodsky M.Ya., Nikitin V.V., Sankin A.I. "İlköğretim matematikte problemlerin toplanması." – M., 1963.

11. Dorofeev G.V., Potapov M.K., Rozov N.Kh. "Matematik El Kitabı". – M., 1973.

12. Shchetnikov A.I. "Pisagor'un sayı ve büyüklük doktrini." – Novosibirsk, 1997.

13. " Gerçek sayılar. İrrasyonel ifadeler" 8. sınıf. Tomsk Üniversitesi Yayınevi. – Tomsk, 1997.

14. Atanasyan M.S. "Geometri" notları 7-9. – M.: Eğitim, 1991.

15. URL: www.moypifagor.narod.ru/

16. URL: http://www.zaitseva-irina.ru/html/f1103454849.html.

Bu okul yılı, eski çağlardan beri bilinen ilginç bir teoremle tanıştım:

"Bir dik üçgenin hipotenüsü üzerine kurulan kare, dik kenarların üzerine inşa edilen karelerin toplamına eşittir."

Bu ifadenin keşfi genellikle antik Yunan filozofu ve matematikçi Pisagor'a (MÖ 6. yüzyıl) atfedilir. Ancak eski el yazmalarının incelenmesi, bu ifadenin Pisagor'un doğumundan çok önce bilindiğini gösterdi.

Bu durumda neden Pisagor adıyla ilişkilendirildiğini merak ettim.

Konunun alaka düzeyi: Pisagor teoremi büyük önem taşımaktadır: geometride kelimenin tam anlamıyla her adımda kullanılır. Pisagor'un eserlerinin bugün hala geçerli olduğuna inanıyorum, çünkü nereye bakarsak bakalım, onun büyük fikirlerinin meyvelerinin modern yaşamın çeşitli dallarında somutlaştığını görebiliriz.

Araştırmamın amacı Pisagor'un kim olduğunu ve bu teoremle ne ilgisi olduğunu bulmaktı.

Teoremin tarihini inceleyerek şunu bulmaya karar verdim:

Bu teoremin başka kanıtları var mı?

Bu teoremin insanların hayatındaki önemi nedir?

Pisagor matematiğin gelişiminde nasıl bir rol oynadı?

Pisagor'un biyografisinden

Samoslu Pisagor büyük bir Yunan bilim adamıdır. Şöhreti Pisagor teoreminin adıyla ilişkilidir. Artık bu teoremin bilindiğini bilmemize rağmen antik Babil Pisagor'dan 1200 yıl önce ve Mısır'da ondan 2000 yıl önce kenarları 3, 4, 5 olan bir dik üçgen biliniyordu, biz ona hâlâ bu kadim bilim adamının adını veriyoruz.

Pisagor'un hayatı hakkında neredeyse hiçbir şey güvenilir bir şekilde bilinmemektedir, ancak onun adı Pythagoras'la ilişkilidir. çok sayıda efsaneler.

Pisagor M.Ö. 570 yılında Samos adasında doğmuştur.

Pisagor güzel bir görünüme sahipti, uzun bir sakalı vardı ve başında altın bir taç vardı. Pisagor bir isim değil, filozofun bir Yunan kehaneti gibi her zaman doğru ve ikna edici konuşması nedeniyle aldığı bir lakaptır. (Pisagor - “konuşarak ikna edici”).

MÖ 550 yılında Pisagor bir karar verir ve Mısır'a gider. Böylece Pisagor'un karşısına bilinmeyen bir ülke, bilinmeyen bir kültür açılıyor. Pisagor bu ülkede çok şaşırdı ve şaşırdı ve Mısırlıların yaşamına ilişkin bazı gözlemlerden sonra Pisagor, rahipler sınıfı tarafından korunan bilgiye giden yolun dinden geçtiğini fark etti.

Pisagor, Mısır'da on bir yıl eğitim gördükten sonra memleketine gider ve bu yolda kendini Babil esaretinde bulur. Orada Mısır'dan daha gelişmiş olan Babil bilimiyle tanıştı. Babilliler doğrusal, ikinci dereceden ve bazı kübik denklem türlerini çözmeyi başardılar. Esaretten kaçtıktan sonra, orada hüküm süren şiddet ve zulüm atmosferi nedeniyle memleketinde uzun süre kalamadı. Croton'a (kuzey İtalya'daki bir Yunan kolonisi) taşınmaya karar verdi.

Pisagor'un hayatındaki en görkemli dönem Croton'da başladı. Orada dini-ahlaksal bir kardeşlik ya da gizli bir manastır tarikatı gibi bir şey kurdu; bu tarikatın üyeleri, sözde Pisagorcu yaşam tarzını sürdürmekle yükümlüydü.

Pisagor ve Pisagorcular

Pisagor, Apennine Yarımadası'nın güneyindeki Yunan kolonisinde, daha sonra Pisagor Birliği olarak adlandırılacak olan manastır tarikatı gibi dini ve ahlaki bir kardeşlik örgütledi. Birliğin üyelerinin belirli ilkelere bağlı kalması gerekiyordu: Birincisi, güzel ve görkemli olan için çabalamak, ikincisi faydalı olmak ve üçüncüsü yüksek zevk için çabalamak.

Pisagor'un öğrencilerine miras bıraktığı ahlaki ve etik kurallar sistemi, Antik Çağ, Orta Çağ ve Rönesans döneminde çok popüler olan Pisagorluların "Altın Ayetleri" nin kendine özgü ahlaki kurallarında derlendi.

Pisagor sınıf sistemi üç bölümden oluşuyordu:

Sayıların öğretilmesi - aritmetik,

Şekiller - geometri ile ilgili öğretiler,

Evrenin yapısıyla ilgili doktrinler - astronomi.

Pisagor'un kurduğu eğitim sistemi yüzyıllarca varlığını sürdürdü.

Pisagor okulu geometriye bir bilim niteliği kazandırmak için çok şey yaptı. Pisagor yönteminin temel özelliği geometri ile aritmetiğin birleşimiydi.

Pisagor oranlar ve ilerlemelerle ve muhtemelen rakamların benzerliğiyle çok uğraştı, çünkü problemi çözdüğüne inanılıyor: “Verilen iki rakamdan, verilerden birine eşit büyüklükte ve ikinciye benzer bir üçüncüyü oluşturun. ”

Pisagor ve öğrencileri çokgen, dost, mükemmel sayılar kavramını tanıttılar ve bunların özelliklerini incelediler. Pisagor, bir hesaplama pratiği olarak aritmetikle ilgilenmiyordu ve gururla "aritmetiği tüccarın çıkarlarının üstünde tuttuğunu" ilan etti.

Pisagor Birliğinin üyeleri Yunanistan'ın birçok şehrinin sakinleriydi.

Pisagorcular da kadınları toplumlarına kabul ettiler. Sendika yirmi yıldan fazla bir süre boyunca gelişti ve ardından üyelerine yönelik zulüm başladı, öğrencilerin çoğu öldürüldü.

Pisagor'un ölümüyle ilgili birçok farklı efsane vardı. Ancak Pisagor ve öğrencilerinin öğretileri yaşamaya devam etti.

Pisagor teoreminin yaratılış tarihinden

Bu teoremin Pisagor tarafından keşfedilmediği artık bilinmektedir. Ancak bazıları bunun tam kanıtını ilk verenin Pisagor olduğuna inanıyor, bazıları ise onun bu değerini inkar ediyor. Bazıları Öklid'in Elementler kitabının ilk kitabında verdiği kanıtları Pisagor'a atfeder. Proclus ise Elementler'deki kanıtın Öklid'e ait olduğunu iddia eder. Gördüğümüz gibi matematik tarihi, Pisagor'un hayatı ve onun matematiksel faaliyetleri hakkında neredeyse hiçbir güvenilir spesifik veriyi korumamıştır.

Pisagor teoreminin tarihsel incelemesine antik Çin ile başlayalım. Burada Özel dikkat Chu-Pei'nin matematik kitabı ilgimi çekti. Bu makale şunu anlatıyor Pisagor üçgeni 3, 4 ve 5. taraflarla:

“Bir dik açı kendisini oluşturan parçalara ayrıştırılırsa, kenarlarının uçlarını birleştiren çizgi 5, taban 3 ve yükseklik 4 olduğunda olacaktır.”

Yapım yöntemlerini çoğaltmak çok kolaydır. 12 m uzunluğunda bir ip alalım ve ona 3 m mesafede renkli bir şerit bağlayalım. bir uçtan ve diğer uçtan 4 metre. Dik açı, 3 ila 4 metre uzunluğundaki kenarlar arasında çevrelenecektir.

Hindular arasında geometri kültle yakından bağlantılıydı. Hipotenüs teoreminin karesi muhtemelen MÖ 8. yüzyılda Hindistan'da zaten biliniyordu. Tamamen ritüel reçetelerin yanı sıra geometrik teolojik nitelikte çalışmalar da var. M.Ö. 4. veya 5. yüzyıla tarihlenen bu yazılarda kenarları 15, 36, 39 olan bir üçgen kullanılarak dik açının inşasına rastlıyoruz.

Orta Çağ'da, Pisagor teoremi mümkün olan en büyük olmasa bile en azından iyi matematik bilgisinin sınırını tanımladı. Artık bazen okul çocukları tarafından örneğin bornoz giymiş bir profesöre veya silindir şapkalı bir adama dönüştürülen Pisagor teoreminin karakteristik çizimi, o günlerde matematiğin sembolü olarak sıklıkla kullanılıyordu.

Sonuç olarak, Pisagor teoreminin Yunanca, Latince ve Almanca'dan çevrilmiş çeşitli formülasyonlarını sunuyoruz.

Öklid teoremi şunu belirtir (literal çeviri):

“Bir dik üçgende, kenarın karesi dik açının üzerine uzanır karelere eşit dik açı içeren kenarlarda."

Gördüğümüz gibi, içinde Farklı ülkeler Ve farklı diller Tanıdık teoremin formülasyonunun farklı versiyonları vardır. Oluşturulma tarihi farklı zaman ve farklı dillerde, kanıtı da çeşitli seçeneklere sahip olan bir matematik yasasının özünü yansıtırlar.

Pisagor teoremini kanıtlamanın beş yolu

Antik Çin kanıtları

Eski Çin çiziminde, ayakları a, b ve hipotenüsü c olan dört eşit dik üçgen, dış konturları a + b kenarlı bir kare oluşturacak ve iç kontur hipotenüs üzerine inşa edilmiş c kenarlı bir kare oluşturacak şekilde düzenlenmiştir.

a2 + 2ab + b2 = c2 + 2ab

J. Hardfield'ın Kanıtı (1882)

İki eşit dik üçgeni birinin ayağı diğerinin devamı olacak şekilde yerleştirelim.

Söz konusu yamuğun alanı, tabanların ve yüksekliğin toplamının yarısının ürünü olarak bulunur.

Öte yandan yamuğun alanı, ortaya çıkan üçgenlerin alanlarının toplamına eşittir:

Bu ifadeleri eşitlersek şunu elde ederiz:

Kanıt basit

Bu kanıt, ikizkenar dik üçgenin en basit durumunda elde edilir.

Muhtemelen teoremin başladığı yer burasıdır.

Aslında teoremin geçerliliğine ikna olmak için ikizkenar dik üçgenler mozaiğine bakmak yeterlidir.

Örneğin ABC üçgeni için: AC hipotenüsü üzerine kurulan kare 4 orijinal üçgen içerir, yanlara kurulan kareler ise iki orijinal üçgen içerir. Teorem kanıtlandı.

Antik Hinduların kanıtı

Kenarı (a + b) olan bir kare, Şekil 2'deki gibi parçalara bölünebilir. 12.a veya Şekil 12.a'daki gibi. 12, b. Her iki resimde de 1, 2, 3, 4 numaralı parçaların aynı olduğu açıktır. Ve eğer eşitleri eşit alanlardan çıkarırsanız, o zaman eşit kalacaklar, yani. c2 = a2 + b2.

Öklid'in kanıtı

İki bin yıl boyunca Pisagor teoreminin en yaygın kullanılan kanıtı Öklid'inkiydi. Ünlü kitabı “İlkeler”de yer almaktadır.

Öklid, BN yüksekliğini dik açının tepesinden hipotenüse indirdi ve devamının, hipotenüs üzerinde tamamlanan kareyi, alanları yanlarda oluşturulan karşılık gelen karelerin alanlarına eşit olan iki dikdörtgene böldüğünü kanıtladı.

Bu teoremi kanıtlamak için kullanılan çizime şaka amaçlı "Pisagor pantolonu" adı veriliyor. Uzun süre matematik biliminin sembollerinden biri olarak kabul edildi.

Pisagor teoreminin uygulanması

Pisagor teoreminin önemi, geometri teoremlerinin çoğunun ondan veya onun yardımıyla türetilebilmesi ve birçok problemin çözülebilmesidir. Ek olarak, Pisagor teoreminin ve onun ters teoreminin pratik önemi, onların yardımıyla, parçaları ölçmeden parçaların uzunluklarını bulabileceğiniz gerçeğinde yatmaktadır. Bu, sanki düz bir çizgiden düzleme, düzlemden hacimsel uzaya ve ötesine giden yolu açar. Giderek daha fazla boyut açmaya ve bu boyutlarda teknolojiler yaratmaya çalışan insanlık için Pisagor teoremi bu nedenle bu kadar önemlidir.

Çözüm

Pisagor teoremi o kadar meşhurdur ki, onu duymamış birinin hayal etmesi zordur. Pisagor teoremini kanıtlamanın birkaç yolu olduğunu öğrendim. İnternetteki bilgiler de dahil olmak üzere bir dizi tarihi ve matematiksel kaynağı inceledim ve Pisagor teoreminin sadece tarihi açısından değil, aynı zamanda yaşamda ve bilimde önemli bir yer tutması nedeniyle de ilginç olduğunu fark ettim. Bu, bu çalışmada sunduğum verilerle kanıtlanmaktadır. çeşitli yorumlar Bu teoremin metni ve ispatının yolu.

Dolayısıyla Pisagor teoremi geometrinin ana ve en önemli teoremlerinden biridir. Önemi, geometri teoremlerinin çoğunun ondan veya onun yardımıyla çıkarılabileceği gerçeğinde yatmaktadır. Pisagor teoremi de dikkat çekicidir çünkü kendi içinde hiç de açık değildir. Örneğin ikizkenar üçgenin özellikleri doğrudan çizimde görülebilir. Ancak bir dik üçgene ne kadar bakarsanız bakın, kenarları arasında basit bir ilişki olduğunu asla göremezsiniz: c2 = a2 + b2. Bu nedenle, bunu kanıtlamak için sıklıkla görselleştirme kullanılır. Pisagor'un değeri, bu teoremin tam bir bilimsel kanıtını vermesiydi. Bu teoremin hafızasını tesadüfen korumadığı bilim insanının kişiliği de ilginçtir. Pisagor harika bir konuşmacı, öğretmen ve eğitimcidir, okulunun organizatörüdür, müzik ve sayıların, iyilik ve adaletin, bilginin ve sağlıklı bir yaşam tarzının uyumuna odaklanmıştır. Biz uzak torunlara örnek teşkil edebilir.

Bibliyografik bağlantı

Tumanova S.V. Pisagor Teoremini Kanıtlamanın Çeşitli Yolları // Bilimle Başlayın. – 2016. – Sayı 2. – S. 91-95;
URL: http://science-start.ru/ru/article/view?id=44 (erişim tarihi: 21.02.2019).

Ev

Pisagor teoremini kanıtlama yöntemleri.

G. Glaser,
Rusya Eğitim Akademisi Akademisyeni, Moskova

Pisagor teoremi ve bunu kanıtlama yöntemleri hakkında

Bir dik üçgenin hipotenüsü üzerine kurulan karenin alanı, dik üçgenin kenarları üzerine kurulan karelerin alanlarının toplamına eşittir...

Bu, Pisagor teoremi olarak adlandırılan antik çağın en ünlü geometrik teoremlerinden biridir. Planimetri eğitimi almış hemen hemen herkes bunu şimdi bile biliyor. Bana öyle geliyor ki, dünya dışı uygarlıkların Dünya'da akıllı yaşamın varlığını bilmesini istiyorsak, o zaman Pisagor figürünün bir görüntüsünü uzaya göndermeliyiz. Düşünen varlıklar bu bilgiyi kabul edebilirlerse, karmaşık sinyal çözme işlemlerine gerek kalmadan Dünya'da oldukça gelişmiş bir medeniyetin olduğunu anlayacaklarını düşünüyorum.

Ünlü Yunan filozofu Teoreme adını veren Samoslu matematikçi Pisagor ise yaklaşık 2,5 bin yıl önce yaşamıştır. Pisagor hakkında bize ulaşan biyografik bilgiler parçalı ve güvenilir olmaktan uzaktır. Birçok efsane onun adıyla ilişkilendirilir. Pisagor'un Doğu ülkelerinde çok seyahat ettiği, Mısır ve Babil'i ziyaret ettiği güvenilir bir şekilde biliniyor. Güney İtalya'daki Yunan kolonilerinden birinde, bilimsel ve siyasi hayatta önemli rol oynayan ünlü "Pisagor Okulu"nu kurdu. Antik Yunan. Ünlü geometrik teoremi kanıtlayan kişi Pisagor'dur. Ünlü matematikçiler (Proclus, Plutarch, vb.) Tarafından yayılan efsanelere dayanarak, uzun süre bu teoremin Pisagor'dan önce bilinmediğine, dolayısıyla Pisagor teoremi adının verildiğine inanılıyordu.

Ancak bu teoremin Pisagor'dan yıllar önce bilindiğine şüphe yoktur. Yani, Pisagor'dan 1500 yıl önce eski Mısırlılar, kenarları 3, 4 ve 5 olan bir üçgenin dik açılı olduğunu biliyorlardı ve planlama yaparken dik açıları oluşturmak için bu özelliği (yani Pisagor teoreminin tersi teoremi) kullandılar. arsalar ve bina yapıları. Bugün bile kırsal kesimdeki inşaatçılar ve marangozlar bir kulübenin temelini atarken ve parçalarını yaparken dik açı elde etmek için bu üçgeni çizerler. Aynı şey binlerce yıl önce Mısır'da, Babil'de, Çin'de ve muhtemelen Meksika'da muhteşem tapınakların inşasında da yapıldı. Pisagor'dan yaklaşık 600 yıl önce yazılmış, bize ulaşan en eski Çin matematik ve astronomi eseri Zhou Bi, dik üçgenle ilgili diğer önerilerin yanı sıra Pisagor teoremini de içerir. Bu teorem daha önce Hindular tarafından biliniyordu. Dolayısıyla Pisagor dik üçgenin bu özelliğini keşfetmedi; muhtemelen bunu genelleyen ve kanıtlayan ilk kişi oydu ve böylece onu uygulama alanından bilim alanına aktardı. Bunu nasıl yaptığını bilmiyoruz. Bazı matematik tarihçileri, Pisagor'un kanıtının temel olmadığını, yalnızca bir doğrulama olduğunu, bu özelliğin, Şekil 2'den açıkça anlaşıldığı ikizkenar dik üçgenle başlayan bir dizi belirli üçgen türü üzerinde bir test olduğunu varsayarlar. 1.

İLE Antik çağlardan beri matematikçiler Pisagor teoreminin giderek daha fazla yeni kanıtını ve onun kanıtı için giderek daha fazla yeni fikir buldular. Bu tür yüz elliden fazla kanıt - az ya da çok katı, az çok görsel - biliniyor, ancak sayılarını artırma arzusu devam ediyor. Pisagor teoreminin kanıtlarının bağımsız olarak "keşfedilmesinin" modern okul çocukları için faydalı olacağını düşünüyorum.

Bu tür aramaların yönünü önerebilecek bazı kanıt örneklerine bakalım.

Pisagor kanıtı

"Bir dik üçgenin hipotenüsü üzerine kurulan kare, dik kenarları üzerine kurulan karelerin toplamına eşittir." Teoremin en basit kanıtı ikizkenar dik üçgenin en basit durumunda elde edilir. Muhtemelen teoremin başladığı yer burasıdır. Aslında teoremin geçerliliğine ikna olmak için ikizkenar dik üçgenler mozaiğine bakmak yeterlidir. Örneğin, DABC için: hipotenüs üzerine kurulmuş bir kare AC, 4 orijinal üçgen ve iki ayak üzerine inşa edilmiş kareler içerir. Teorem kanıtlandı.

Şekillerin eşit büyüklükte olması kavramının kullanımına dayalı ispatlar.

Bu durumda, belirli bir dik üçgenin hipotenüsü üzerine inşa edilen bir karenin, yan taraflara inşa edilen karelerle aynı şekillerden "oluştuğunu" kanıtlayabiliriz. Ayrıca rakamların toplamlarının yeniden düzenlenmesini kullanan ve bir takım yeni fikirleri hesaba katan kanıtları da değerlendirebiliriz.

İncirde. Şekil 2 iki eşit kareyi göstermektedir. Her karenin kenar uzunluğu a + b'dir. Karelerin her biri kareler ve dik üçgenlerden oluşan parçalara bölünmüştür. Bacakları a, b olan bir dik üçgenin dörtlü alanı karenin alanından çıkarılırsa eşit alanların kalacağı açıktır, yani. c 2 = a 2 + b 2 . Ancak bu düşüncenin ait olduğu eski Hindular genellikle bunu yazmadılar ve çizime tek bir kelimeyle eşlik ettiler: "bak!" Pisagor'un da aynı kanıtı sunması oldukça olasıdır.

İlave kanıtlar.

Bu kanıtlar, bacaklar üzerine inşa edilmiş karelerin, hipotenüs üzerine inşa edilmiş bir karenin eklenebileceği rakamlara ayrıştırılmasına dayanmaktadır.

Burada: ABC, dik açısı C olan bir dik üçgendir; CMN; CKMN; PO||MN; EF||MN.

Bacaklar ve hipotenüs üzerine inşa edilen karelerin bölünmesiyle elde edilen üçgenlerin ikili eşitliğini bağımsız olarak kanıtlayın.

Bu bölümü kullanarak teoremi kanıtlayın.

 Neyriziye'nin ispatına dayanarak, karelerin ikili eşit rakamlara başka bir ayrıştırması gerçekleştirildi (Şekil 5, burada ABC, C dik açılı bir dik üçgendir).

 “Bıçaklı tekerlek” adı verilen kareleri eşit parçalara ayırma yönteminin bir başka kanıtı Şekil 2'de gösterilmektedir. 6. Burada: ABC, C dik açısına sahip bir dik üçgendir; O geniş bir kenar üzerine kurulu karenin merkezidir; O noktasından geçen noktalı çizgiler hipotenüse dik veya paraleldir.

 Karelerin bu şekilde ayrıştırılması ilginçtir çünkü ikili eşit dörtgenler paralel öteleme yoluyla birbirleri üzerine eşlenebilir. Pisagor teoreminin diğer birçok kanıtı, karelerin rakamlara ayrıştırılması kullanılarak sunulabilir.

Tamamlama yöntemiyle kanıt.

Bu yöntemin özü, bacaklar üzerine kurulan karelere ve hipotenüs üzerine kurulan kareye eşit rakamların eklenmesiyle eşit rakamlar elde edilmesidir.

Pisagor teoreminin geçerliliği, AEDFPB ve ACBNMQ altıgenlerinin eşit büyüklükte olmasından kaynaklanmaktadır. Burada CEP, EP doğrusu AEDFPB altıgenini iki eşit dörtgene böler, CM çizgisi ACBNMQ altıgenini iki eşit dörtgene böler; Düzlemin A merkezi etrafında 90° döndürülmesi, dörtgen AEPB'yi dörtgen ACMQ'ya eşler.

İncirde. 8 Pisagor figürü, kenarları, yanlarda oluşturulan karelerin karşılık gelen kenarlarına paralel olan bir dikdörtgen şeklinde tamamlanmıştır. Bu dikdörtgeni üçgenlere ve dikdörtgenlere bölelim. Ortaya çıkan dikdörtgenden ilk önce tüm 1, 2, 3, 4, 5, 6, 7, 8, 9 çokgenlerini çıkarıyoruz ve hipotenüs üzerinde kurulu bir kare bırakıyoruz. Daha sonra aynı dikdörtgenden 5, 6, 7 numaralı dikdörtgenleri ve gölgeli dikdörtgenleri çıkarıyoruz, bacaklar üzerine kurulmuş kareler elde ediyoruz.

Şimdi birinci durumda çıkarılan rakamların ikinci durumda çıkarılan rakamlara eşit büyüklükte olduğunu kanıtlayalım.

KLOA = ACPF = ACED = a 2;

LGBO = CBMP = CBNQ = b2;

AKGB = AKLO + LGBO = c2;

dolayısıyla c 2 = a 2 + b 2 .

OCLP = ACLF = ACED = b2;

CBML = CBNQ = a 2;

OBMP = ABMF = c2;

OBMP = OCLP + CBML;

c2 = a2 + b2 .

Cebirsel ispat yöntemi.

	Pirinç. Şekil 12, büyük Hintli matematikçi Bhaskari'nin (ünlü yazar Lilavati, X) kanıtını göstermektedir. II. yüzyıl). Çizime tek bir kelime eşlik ediyordu: BAKIN! Pisagor teoreminin cebirsel yöntemle ispatları arasında ilk sırayı (belki de en eskisi) benzerlik kullanan ispat alır.
	Bu kanıtlardan birini Pisagor'a dayanarak modern bir sunumla sunalım.

N ve incir. 13 ABC – dikdörtgen, C – dik açı, CMAB, b 1 – b bacağının hipotenüse izdüşümü, a 1 – a bacağının hipotenüse izdüşümü, h – üçgenin hipotenüse çizilen yüksekliği.

ABC'nin ACM'ye benzer olması gerçeğinden şu sonuç çıkar:

b2 = cb1; (1)

ABC'nin BCM'ye benzer olması gerçeğinden şu sonuç çıkar:

a 2 = yaklaşık 1. (2)

(1) ve (2) eşitliklerini terim terim toplayarak a 2 + b 2 = cb 1 + ca 1 = c(b 1 + a 1) = c 2 elde ederiz.

Eğer Pisagor böyle bir kanıt sunmuşsa, o aynı zamanda modern matematik tarihçilerinin genellikle Öklid'e atfettiği bir takım önemli geometrik teoremlere de aşinaydı.

Moehlmann'ın kanıtı (Şekil 14). Belirli bir dik üçgenin alanı, bir yandan diğerine eşittir; burada p, üçgenin yarı çevresidir, r, içine yazılan dairenin yarıçapıdır. Sahibiz:

buradan c 2 =a 2 +b 2 sonucu çıkar.

saniyede

Bu ifadeleri eşitleyerek Pisagor teoremini elde ederiz.

Kombine yöntem

Üçgenlerin eşitliği

c2 = a2 + b2 . (3)

(3) ve (4) ilişkilerini karşılaştırarak şunu elde ederiz:

c 1 2 = c 2 veya c 1 = c.

Böylece, verilen üçgen ve oluşturulan üçgenler eşittir, çünkü üç kenarları sırasıyla eşittir. C 1 açısı dik olduğundan bu üçgenin C açısı da diktir.

Eski Hint kanıtları.

Eski Hindistan matematikçileri, Pisagor teoremini kanıtlamak için eski bir Çin çiziminin iç kısmını kullanmanın yeterli olduğunu fark ettiler. 19. yüzyılın en büyük Hintli matematikçisinin palmiye yaprakları üzerine yazdığı “Siddhanta Shiromani” (“Bilginin Tacı”) adlı eserinde. Bha-skaralar bir çizime yerleştirilmiştir (Şekil 4)

Hint kanıtlarının özelliği "bak!" kelimesidir. Gördüğünüz gibi dik üçgenler buraya hipotenüs dışarı bakacak şekilde ve bir kare şeklinde döşeniyor. İle 2 “gelin sandalyesine” aktarıldı İle 2 -B 2 . Pisagor teoreminin özel durumlarına (örneğin, alanı iki kat daha büyük bir kare oluşturmak) dikkat edin. Şekil 4 belirli bir karenin alanı) eski Hint incelemesi "Sulva" da bulunur

Bir dik üçgeni ve onun ayakları üzerine kurulmuş kareleri, yani 16 adet eş ikizkenar dik üçgenden oluşan ve dolayısıyla kareye sığan şekilleri çözdük. Lily de böyle. Antik matematiğin incisi olan Pisagor teoreminde saklı zenginliğin küçük bir kısmı.

Eski Çin kanıtları.

Antik Çin'in matematik incelemeleri 2. yüzyılın baskısında bize geldi. M.Ö. Gerçek şu ki, MÖ 213'te. Önceki gelenekleri ortadan kaldırmaya çalışan Çin İmparatoru Shi Huang Di, tüm eski kitapların yakılmasını emretti. P yüzyılda M.Ö. Çin'de kağıt icat edildi ve aynı zamanda eski kitapların yeniden inşası başladı.Günümüze kalan astronomi eserlerinden en önemlisi, Pisagor teoremini kanıtlayan bir çizim (Şekil 2, a) içeren “Matematik” kitabıdır. Bu kanıtın anahtarını bulmak zor değil. Aslında eski Çin çiziminde kenarları a, b ve hipotenüsleri olan dört eşit dik açılı üçgen vardır. İle yığılmış G) böylece dış hatları Şekil 2'de kenarları olan bir kare oluşturacak şekilde a+b, içteki ise hipotenüs üzerine kurulmuş, kenarı c olan bir karedir (Şekil 2, b). Kenarı c olan bir kare kesilip kalan 4 gölgeli üçgen iki dikdörtgenin içine yerleştirilirse (Şekil 2, V), o zaman ortaya çıkan boşluğun bir yandan şuna eşit olduğu açıktır: İLE 2 , ve diğer tarafta - İle 2 +b 2 , onlar. c 2=  2 +b 2 . Teorem kanıtlandı. Bu ispatla, eski Çin çiziminde gördüğümüz (Şekil 2, a) hipotenüs üzerindeki karenin içindeki yapıların kullanılmadığına dikkat edin. Görünüşe göre eski Çinli matematikçilerin farklı bir kanıtı vardı. Kesinlikle kenarı olan bir kare ise İle iki gölgeli üçgen (Şekil 2, B) Hipotenüsleri kesin ve diğer iki hipotenüse ekleyin (Şekil 2, G), o zaman bunu keşfetmek kolaydır

Bazen "gelin sandalyesi" olarak da adlandırılan ortaya çıkan figür, kenarları olan iki kareden oluşur. A Ve B, onlar. C 2 == A 2 +b 2 .

N ve Şekil 3'te "Zhou-bi..." incelemesinden bir çizim gösterilmektedir. Burada Pisagor teoremi, bacakları 3, 4 olan ve hipotenüsü 5 birim olan Mısır üçgeni için ele alınmıştır. Hipotenüs üzerindeki kare 25 hücre içerir ve büyük kenardaki karede 16 hücre bulunur. Geriye kalan kısmın 9 hücreden oluştuğu açıktır. Bu küçük taraftaki kare olacak.