Összetett függvény grafikonjainak ábrázolása transzformációk segítségével. Grafikonok konvertálása
Hipotézis: Ha megvizsgálja a gráf mozgását a függvényegyenlet kialakítása során, észre fogja venni, hogy minden gráf engedelmeskedik általános minták ezért megfogalmazhatjuk általános törvények Függvényektől függetlenül, ami nemcsak megkönnyíti a különböző függvények grafikonjainak elkészítését, hanem a feladatok megoldásában is felhasználja azokat.
Cél: Függvénygráfok mozgásának tanulmányozása:
1) A feladat az irodalom tanulmányozása
2) Tanuljon meg különféle függvények grafikonjait összeállítani
3) Tanulja meg lineáris függvények grafikonjait átalakítani
4) Vegye figyelembe a grafikonok használatának kérdését a feladatok megoldása során
Vizsgálat tárgya: Függvénygráfok
Kutatás tárgya: Függvénygráfok mozgása
Relevancia: A függvénygráfok készítése általában sok időt vesz igénybe, és figyelmet igényel a hallgató részéről, de a függvénygráfok és az alapvető függvények grafikonjainak konvertálására vonatkozó szabályok ismeretében gyorsan és egyszerűen készíthet függvénygráfokat. , amely lehetővé teszi, hogy ne csak a függvények grafikonjainak elkészítéséhez szükséges feladatokat hajtsa végre, hanem az ezzel kapcsolatos problémákat is megoldja (a maximum megtalálása (minimális időmagasság és találkozási pont))
Ez a projekt az iskola minden tanulója számára hasznos.
Irodalmi áttekintés:
A szakirodalom tárgyalja a különféle függvények gráfjainak elkészítésének módszereit, valamint példákat e függvények gráfjainak transzformációjára. Szinte az összes alapvető függvény grafikonjait különféle esetekben használják technikai folyamatok, amely lehetővé teszi a folyamat tisztábban történő megjelenítését és az eredmény programozását
Állandó funkció. Ezt a függvényt az y = b képlet adja meg, ahol b egy bizonyos szám. Egy konstans függvény grafikonja egy az abszcisszával párhuzamos, az ordináta (0; b) pontján átmenő egyenes. Az y = 0 függvény grafikonja az x tengely.
A függvény típusai 1 Közvetlen arányosság. Ezt a függvényt az y = kx képlet adja meg, ahol az arányossági együttható k ≠ 0. Az egyenes arányosság grafikonja az origón áthaladó egyenes.
Lineáris függvény. Egy ilyen függvényt az y = kx + b képlet ad meg, ahol k és b valós számok. A lineáris függvény grafikonja egy egyenes.
A lineáris függvények grafikonjai metszhetik egymást vagy párhuzamosak lehetnek.
Így az y = k 1 x + b 1 és y = k 2 x + b 2 lineáris függvények grafikonjainak egyenesei metszik egymást, ha k 1 ≠ k 2 ; ha k 1 = k 2, akkor az egyenesek párhuzamosak.
2A fordított arányosság egy olyan függvény, amelyet az y = k/x képlet ad meg, ahol k ≠ 0. K-t együtthatónak nevezzük fordított arányosság. A fordított arányosság grafikonja egy hiperbola.
Az y = x 2 függvényt egy parabolának nevezett gráf ábrázolja: a [-~; 0] a függvény csökken, az intervallumon a függvény növekszik.
Az y = x 3 függvény a teljes számegyenesen növekszik, és grafikusan egy köbös parabolával ábrázoljuk.
Hatványfüggvény természetes kitevővel. Ezt a függvényt az y = x n képlet adja meg, ahol n értéke természetes szám. Diagramok teljesítmény funkció természetes kitevőjével n-től függ. Például, ha n = 1, akkor a gráf egy egyenes lesz (y = x), ha n = 2, akkor a gráf egy parabola stb.
A negatív egész kitevővel rendelkező hatványfüggvényt az y = x -n képlet ábrázolja, ahol n természetes szám. Ez a függvény minden x ≠ 0 esetén definiálva van. A függvény grafikonja az n kitevőtől is függ.
Hatványfüggvény pozitív tört kitevővel. Ezt a függvényt az y = x r képlet ábrázolja, ahol r egy pozitív irreducibilis tört. Ez a függvény sem páros, sem nem páratlan.
Egy vonaldiagram, amely a függő és független változók kapcsolatát jeleníti meg a koordinátasíkon. A grafikon ezen elemek vizuális megjelenítésére szolgál
A független változó olyan változó, amely tetszőleges értéket vehet fel a függvénydefiníció tartományában (ahol az adott függvénynek van jelentése (nem osztható nullával))
A szükséges függvények grafikonjának elkészítéséhez
1) Keresse meg a VA-t (az elfogadható értékek tartománya)
2) vegyen fel több tetszőleges értéket a független változóhoz
3) Határozza meg a függő változó értékét!
4) Építeni Koordináta sík jelölje meg rajta ezeket a pontokat
5) Szükség esetén kösse össze vonalaikat, vizsgálja meg a kapott gráfot Gráfok transzformációja elemi függvények.
Grafikonok konvertálása
Az alapvető elemi funkciók tiszta formában sajnos nem olyan gyakoriak. Sokkal gyakrabban kell az alapvető elemi függvényekből konstansok és együtthatók hozzáadásával nyert elemi függvényekkel foglalkozni. Az ilyen függvények grafikonjait a megfelelő alapvető elemi függvények grafikonjaira geometriai transzformációk alkalmazásával (vagy új koordináta-rendszerre váltással) lehet megszerkeszteni. Például, másodfokú függvény a képlet az másodfokú parabola az ordináta tengelyéhez képest háromszor tömörített, az abszcissza tengelyhez képest szimmetrikusan megjelenített képlet, ennek a tengelynek az irányával szemben 2/3 egységgel eltolva, és az ordináta tengelye mentén 2 egységgel eltolva.
Lépésről lépésre értelmezzük egy függvény grafikonjának ezeket a geometriai transzformációit konkrét példák segítségével.
Az f(x) függvény gráfjának geometriai transzformációival elkészíthető bármely formaképletű függvény gráfja, ahol a képlet az oy, illetve az ox tengely menti tömörítési vagy nyújtási együttható, az előtte lévő mínusz jelek. A képlet és a képlet együtthatók a grafikonnak a koordinátatengelyekhez viszonyított szimmetrikus megjelenítését jelzik, a és b határozza meg az abszcissza, illetve az ordináta tengelyekhez viszonyított eltolódást.
Így egy függvény grafikonjának háromféle geometriai transzformációja létezik:
Az első típus a méretezés (kompresszió vagy nyújtás) az abszcissza és az ordináta tengelyek mentén.
A méretezés szükségességét az egytől eltérő képletegyüttható jelzi; ha a szám kisebb, mint 1, akkor a grafikont oy-hoz képest tömörítjük és oxhoz képest megnyújtjuk; ha a szám nagyobb, mint 1, akkor az ordináta tengelye mentén nyújtjuk és az abszcissza tengelye mentén összenyomjuk.
A második típus a koordinátatengelyekhez képest szimmetrikus (tükrös) megjelenítés.
Ennek az átalakításnak a szükségességét jelzik a képlet együtthatói előtti mínusz jelek (ebben az esetben szimmetrikusan jelenítjük meg a grafikont az ökör tengelye körül) és a képlet (ebben az esetben szimmetrikusan jelenítjük meg a grafikont az oy körül tengely). Ha nincsenek mínuszjelek, akkor ez a lépés kimarad.








 Vissza előre
Vissza előre
Figyelem! A dia-előnézetek csak tájékoztató jellegűek, és nem feltétlenül képviselik a prezentáció összes jellemzőjét. Ha érdekel ez a munka, töltse le a teljes verziót.
Az óra célja: Határozza meg a függvénygráfok transzformációs mintáit!
Feladatok:
Nevelési:
- Tanítsa meg a tanulókat függvénygráfok készítésére egy adott függvény grafikonjának átalakításával, párhuzamos fordítással, tömörítéssel (nyújtással), különböző fajták szimmetria.
Nevelési:
- A tanulók személyes tulajdonságainak (a meghallgatás képességének), másokkal szembeni jóindulatnak, figyelmességnek, pontosságnak, fegyelmezettségnek, csoportmunkára való képességének ápolása.
- Fokozza a tárgy iránti érdeklődést és az ismeretek megszerzésének szükségességét.
Fejlődési:
- Fejleszti a térbeli képzelőerőt és logikus gondolkodás tanulók, a környezetben való gyors eligazodás képessége; fejleszti az intelligenciát, a találékonyságot és fejleszti a memóriát.
Felszerelés:
- Multimédia telepítés: számítógép, projektor.
Irodalom:
- Bashmakov, M. I. Matematika [Szöveg]: tankönyv kezdő intézmények számára. és szerda prof. oktatás / M.I. Bashmakov. - 5. kiadás, átdolgozott. – M.: „Akadémia” Kiadói Központ, 2012. – 256 p.
- Bashmakov, M. I. Matematika. Problémakönyv [Szöveg]: tankönyv. oktatási pótlék intézmények korán és szerda prof. oktatás / M. I. Bashmakov. – M.: Kiadói Központ „Akadémia”, 2012. – 416 p.
Tanterv:
- Szervezési pillanat (3 perc).
- Tudásfrissítés (7 perc).
- Új anyag magyarázata (20 perc).
- Új anyag tömörítése (10 perc).
- Óra összefoglalója (3 perc).
- Házi feladat(2 perc).
Az órák alatt
1. Org. pillanat (3 perc).
A jelenlévők ellenőrzése.
Közölje az óra célját.
A függvények alapvető tulajdonságai, mint a változó mennyiségek közötti függőségek, nem változhatnak jelentősen ezeknek a mennyiségeknek a mérési módjának megváltoztatásakor, azaz a mérési skála és a referenciapont megváltoztatásakor. A változó mennyiségek mérési módszerének ésszerűbb megválasztása miatt azonban általában lehetséges a köztük lévő kapcsolat rögzítése egyszerűsíteni, és ezt a rögzítést valamilyen szabványos formába hozni. Geometriai nyelven az értékek mérési módjának megváltoztatása a grafikonok néhány egyszerű transzformációját jelenti, amelyeket ma tanulmányozni fogunk.
2. Ismeretek felfrissítése (7 perc).
Mielőtt a gráftranszformációkról beszélnénk, tekintsük át az általunk tárgyalt anyagot.
Szóbeli munka. (2. dia).
Adott funkciók:
3. Ismertesse a függvények grafikonjait: , , , .
3. Új anyag magyarázata (20 perc).
A gráfok legegyszerűbb átalakítása a párhuzamos átvitel, a tömörítés (nyújtás) és a szimmetria egyes típusai. Néhány átalakítás a táblázatban látható (1. melléklet), (3. dia).
Csoportokban dolgoznak.
Minden csoport grafikont készít adott függvényekről, és bemutatja az eredményt megbeszélésre.
| Funkció | Egy függvény grafikonjának átalakítása | Funkciópéldák | Csúszik |
| OU tovább A egységekkel feljebb, ha A>0, és |A| egységekkel lefelé, ha A<0. | , | (4. dia)
|
|
| Párhuzamos átvitel a tengely mentén Ó tovább A egységekkel jobbra, ha A>0, és tovább - A egységgel balra, ha A<0. | , | (5. dia)
|
A fizikai folyamatok körülményeitől függően egyes mennyiségek állandó értéket vesznek fel, és konstansnak nevezik, mások bizonyos körülmények között változnak, és változóknak nevezik.
A környezet gondos tanulmányozása azt mutatja, hogy a fizikai mennyiségek függnek egymástól, vagyis bizonyos mennyiségek változása más mennyiségek változását vonja maga után.
A matematikai elemzés a kölcsönösen változó mennyiségek közötti kvantitatív összefüggések vizsgálatával foglalkozik, elvonatkoztatva a konkrét fizikai jelentéstől. A matematikai elemzés egyik alapfogalma a függvény fogalma.
Tekintsük a halmaz elemeit és a halmaz elemeit  (3.1. ábra).
(3.1. ábra).

Ha a halmazok elemei között valamilyen megfeleltetés jön létre  És
És  szabály formájában
szabály formájában  , akkor megjegyzik, hogy a függvény definiálva van
, akkor megjegyzik, hogy a függvény definiálva van  .
.
Meghatározás
3.1.
Levelezés  , amely az egyes elemekhez kapcsolódik
, amely az egyes elemekhez kapcsolódik  nem üres készlet
nem üres készlet  valami jól körülhatárolható elem
valami jól körülhatárolható elem  nem üres készlet
nem üres készlet  függvénynek vagy leképezésnek nevezik
függvénynek vagy leképezésnek nevezik  V
V  .
.
Szimbolikusan megjeleníteni  V
V  a következőképpen van írva:
a következőképpen van írva:
 .
.
Ugyanakkor sokan  a függvény definíciós tartományának nevezzük és jelöljük
a függvény definíciós tartományának nevezzük és jelöljük  .
.
Viszont sok  a függvény értéktartományának nevezzük, és jelöljük
a függvény értéktartományának nevezzük, és jelöljük  .
.
Ezen kívül meg kell jegyezni, hogy a készlet elemei  független változóknak, a halmaz elemeinek nevezzük
független változóknak, a halmaz elemeinek nevezzük  függő változóknak nevezzük.
függő változóknak nevezzük.
Funkció megadásának módszerei
A függvény a következő főbb módokon adható meg: táblázatos, grafikus, analitikus.
Ha kísérleti adatok alapján olyan táblázatokat állítanak össze, amelyek a függvény értékeit és a megfelelő argumentumértékeket tartalmazzák, akkor a függvény megadásának ezt a módszerét táblázatosnak nevezzük.
Ugyanakkor, ha a kísérleti eredmény egyes tanulmányait rögzítőn (oszcilloszkóp, felvevő stb.) jelenítik meg, akkor meg kell jegyezni, hogy a funkció grafikusan van megadva.
A legelterjedtebb a függvény megadásának analitikus módja, pl. olyan módszer, amelyben egy független és függő változót egy képlet segítségével kapcsolunk össze. Ebben az esetben a függvény definíciós tartománya jelentős szerepet játszik:
különbözőek, bár ugyanazok az elemzési viszonyok adják őket.
Ha csak a függvényképletet adja meg  , akkor úgy tekintjük, hogy ennek a függvénynek a definíciós tartománya egybeesik a változó értékeinek halmazával
, akkor úgy tekintjük, hogy ennek a függvénynek a definíciós tartománya egybeesik a változó értékeinek halmazával  , amelyre a kifejezés
, amelyre a kifejezés  jelentése van. Ebben a tekintetben különleges szerepet játszik a függvény definíciós tartományának megtalálásának problémája.
jelentése van. Ebben a tekintetben különleges szerepet játszik a függvény definíciós tartományának megtalálásának problémája.
Feladat 3.1. Keresse meg egy függvény tartományát

Megoldás
Az első tag valós értékeket vesz fel, amikor  , a második pedig at. Tehát egy adott függvény definíciós tartományának megtalálásához meg kell oldani az egyenlőtlenségek rendszerét:
, a második pedig at. Tehát egy adott függvény definíciós tartományának megtalálásához meg kell oldani az egyenlőtlenségek rendszerét:

Ennek eredményeként egy ilyen rendszer megoldása születik. Ezért a függvény definíciós tartománya a szegmens  .
.
A függvénygráfok legegyszerűbb transzformációi
A függvénygráfok felépítése jelentősen leegyszerűsíthető, ha az alapvető elemi függvények jól ismert gráfjait használjuk. A következő függvényeket fő elemi függvényeknek nevezzük:
1) teljesítmény funkció  Ahol
Ahol  ;
;
2)exponenciális függvény Ahol
Ahol 
 És
És  ;
;
3) logaritmikus függvény  , Ahol
, Ahol  - egytől eltérő bármely pozitív szám:
- egytől eltérő bármely pozitív szám:  És
És  ;
;
4) trigonometrikus függvények 



 ;
;
 .
.
5) inverz trigonometrikus függvények  ;
; ;
;
 ;
;
 .
.
Az elemi függvények olyan függvények, amelyeket az alapvető elemi függvényekből kapunk négy aritmetikai művelettel és véges számú szuperpozícióval.
Az egyszerű geometriai transzformációk lehetővé teszik a függvénygráfok készítésének folyamatának egyszerűsítését is. Ezek az átalakítások a következő állításokon alapulnak:
Az y=f(x+a) függvény grafikonja az y=f(x) grafikon, eltolva (>0 esetén balra,< 0 вправо) на |a| единиц параллельно осиOx.
Az y=f(x) +b függvény grafikonja az y=f(x) grafikonja, eltolva (b>0-nál felfelé, b-nél< 0 вниз) на |b| единиц параллельно осиOy.
Az y = mf(x) (m0) függvény grafikonja az y = f(x) grafikonja, m-szer kinyújtva (m>1) vagy tömörítve (0-nál). Az y = f(kx) függvény grafikonja az y = f(x) grafikonja, k-szer tömörítve (k >1 esetén) vagy kinyújtva (0 esetén< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx)
есть зеркальное отображение графика
y = f(–kx) от оси Oy.
Az alapvető elemi függvények tiszta formájukban, transzformáció nélkül ritkák, ezért leggyakrabban olyan elemi függvényekkel kell dolgozni, amelyeket a fő függvényekből kaptunk állandók és együtthatók hozzáadásával. Az ilyen gráfok adott elemi függvények geometriai transzformációival készülnek.
Tekintsünk egy példát egy y = - 1 3 x + 2 3 2 + 2 alakú másodfokú függvényre, melynek grafikonja az y = x 2 parabola, amely Oy-hoz képest háromszor van tömörítve, és szimmetrikus az Oy-hez képest. Ox-ra, és 2 3-mal eltolva az Ox mentén jobbra, 2 egységgel feljebb az Oy mentén. Egy koordináta egyenesen így néz ki:
Yandex.RTB R-A-339285-1
Egy függvény gráfjának geometriai transzformációi
Adott gráf geometriai transzformációit alkalmazva azt kapjuk, hogy a gráfot ± k 1 · f (± k 2 · (x + a)) + b alakú függvény ábrázolja, ha k 1 > 0, k 2 > 0 a kompressziós együtthatók 0-nál vannak< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 O y és O x mentén. A k 1 és k 2 együtthatók előtti jel a grafikon tengelyekhez viszonyított szimmetrikus megjelenítését jelzi, a és b eltolja O x és O y mentén.
1. definíció
3 típusa van a gráf geometriai transzformációi:
- Méretezés O x és O y mentén. Ezt befolyásolják a k 1 és k 2 együtthatók, feltéve, hogy nem egyenlők 1-gyel, ha 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, akkor a grafikont O y mentén megnyújtjuk és O x mentén összenyomjuk.
- Szimmetrikus kijelzés a koordinátatengelyekhez viszonyítva. Ha k 1 előtt „-” jel van, akkor a szimmetria O x-hez, k 2 előtt pedig O y-hoz viszonyított. Ha a „-” hiányzik, akkor az elem kihagyásra kerül a megoldás során;
- Párhuzamos átvitel (eltolás) O x és O y mentén. A transzformációt akkor hajtjuk végre, ha az a és b együttható nem egyenlő 0-val. Ha a pozitív, a grafikon balra tolódik | a | egységek, ha a negatív, akkor jobbra ugyanabban a távolságban. A b érték határozza meg az O y tengely mentén történő mozgást, ami azt jelenti, hogy ha b pozitív, akkor a függvény felfelé, ha b negatív, akkor lefelé mozog.
Nézzük meg a megoldásokat példákon keresztül, kezdve egy hatványfüggvénnyel.
1. példa
Alakítsa át y = x 2 3 és ábrázolja az y = - 1 2 · 8 x - 4 2 3 + 3 függvényt.
Megoldás
A függvényeket a következőképpen ábrázoljuk:
y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3
Ahol k 1 = 2, érdemes figyelni a „-”, a = - 1 2, b = 3 jelenlétére. Innen azt kapjuk, hogy a geometriai transzformációkat O y mentén kétszeri nyújtással hajtjuk végre, O x-hez képest szimmetrikusan megjelenítve, 1 2-vel jobbra és 3 egységgel felfelé tolva.
Ha az eredeti hatványfüggvényt ábrázoljuk, azt kapjuk

amikor kétszer megnyújtjuk O y mentén megvan az

Az O x-hez képest szimmetrikus leképezésnek megvan a formája

és haladjon jobbra 1 2-vel

3 egységnyi mozgás felfelé úgy néz ki

Nézzük meg az exponenciális függvények transzformációit példákon keresztül.
2. példa
Szerkesszük meg az y = - 1 2 1 2 (2 - x) + 8 exponenciális függvény grafikonját!
Megoldás.
Alakítsuk át a függvényt egy hatványfüggvény tulajdonságai alapján. Akkor azt kapjuk
y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8
Ebből láthatjuk, hogy y = 1 2 x transzformációs láncot kapunk:
y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8
Azt találjuk, hogy az eredeti exponenciális függvénynek van alakja

O y mentén kétszer összenyomva ad

O x mentén nyújtózva
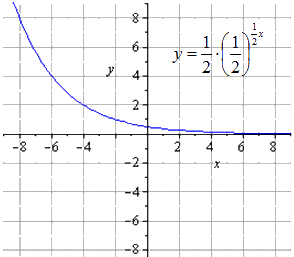
Szimmetrikus leképezés O x vonatkozásában

A leképezés szimmetrikus O y-hoz képest

Lépj feljebb 8 egységgel

Tekintsük a megoldást egy y = ln (x) logaritmikus függvény példáján.
3. példa
Szerkesszük meg az y = ln e 2 · - 1 2 x 3 függvényt az y = ln (x) transzformáció segítségével.
Megoldás
A megoldáshoz a logaritmus tulajdonságait kell használni, ekkor kapjuk:
y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2
A logaritmikus függvény transzformációi így néznek ki:
y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2
Ábrázoljuk az eredeti logaritmikus függvényt

O y szerint tömörítjük a rendszert

O x mentén nyújtózunk

Leképezést végzünk O y vonatkozásában

2 egységgel feljebb toljuk, megkapjuk

Grafikonok konvertálásához trigonometrikus függvény± k 1 · f (± k 2 · (x + a)) + b alakú megoldási sémát kell illeszteni. Szükséges, hogy k 2 egyenlő legyen T k 2 -vel. Innentől azt kapjuk, hogy 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.
Nézzünk példákat a problémák megoldására y = sin x transzformációkkal.
4. példa
Szerkesszük meg y = - 3 sin 1 2 x - 3 2 - 2 gráfját az y=sinx függvény transzformációival.
Megoldás
Szükséges a függvényt ± k 1 · f ± k 2 · x + a + b alakra redukálni. Ezért:
y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2
Látható, hogy k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Mivel k 1 előtt van „-”, de k 2 előtt nincs, így a következő alakzatú transzformációk láncát kapjuk:
y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2
Részletes szinuszos transzformáció. Az eredeti y = sin (x) szinusz ábrázolásakor azt találjuk, hogy a legkisebb pozitív periódusnak tekintjük T = 2 π. A maximum megkeresése a π 2 + 2 π · k pontokban; 1, és a minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

Az O y háromszorosára nyúlik, ami azt jelenti, hogy az oszcillációk amplitúdójának növekedése 3-szorosára nő. T = 2 π a legkisebb pozitív periódus. A maximumok π 2 + 2 π · k; 3, k ∈ Z, minimumok - - π 2 + 2 π · k; - 3, k ∈ Z.
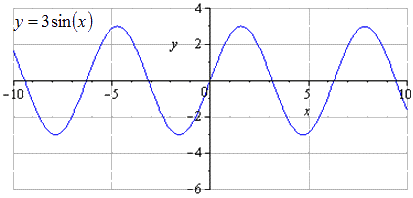
Ha az O x mentén felére nyújtunk, azt tapasztaljuk, hogy a legkisebb pozitív periódus kétszeresére nő, és egyenlő a T = 2 π k 2 = 4 π értékkel. A maximumok π + 4 π · k; 3, k ∈ Z, minimumok – in - π + 4 π · k; - 3, k ∈ Z.

A kép O x-hez képest szimmetrikusan jön létre. A legkisebb pozitív időszak ben ebben az esetben nem változik és egyenlő T = 2 π k 2 = 4 π . A maximális átmenet így néz ki: - π + 4 π · k; 3, k ∈ Z, és a minimum π + 4 π · k; - 3, k ∈ Z.
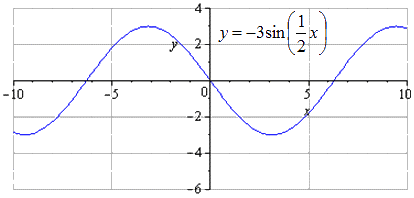
A grafikon 2 egységgel lefelé tolódik el. A minimális közös időszak nem változik. Maximum keresése pontokba való átmenettel - π + 3 + 4 π · k; 1, k ∈ Z, minimumok - π + 3 + 4 π · k; - 5 , k ∈ Z .

Tovább ezen a ponton egy trigonometrikus függvény grafikonját transzformáltnak tekintjük.
Tekintsük az y = cos x függvény részletes transzformációját.
5. példa
Szerkesszük meg az y = 3 2 cos 2 - 2 x + 1 függvény gráfját az y = cos x formájú függvénytranszformáció segítségével.
Megoldás
Az algoritmus szerint az adott függvényt ± k 1 · f ± k 2 · x + a + b alakra kell redukálni. Akkor azt kapjuk
y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1
A feltételből jól látható, hogy k 1 = 3 2, k 2 = 2, a = - 1, b = 1, ahol k 2-ben van „-”, de k 1 előtt hiányzik.
Ebből azt látjuk, hogy a következő alakú trigonometrikus függvény grafikonját kapjuk:
y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1
Lépésről lépésre koszinusz transzformáció grafikus illusztrációval.
Az y = cos(x) grafikon alapján világos, hogy a legrövidebb teljes periódus T = 2π. Maximum keresése 2 π · k-ben; 1, k ∈ Z, és van π + 2 π · k minimum; - 1, k ∈ Z.
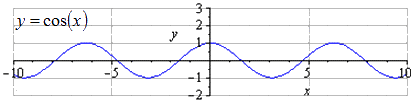
Ha Oy mentén 3 2-szeresre feszítjük, az oszcillációk amplitúdója 32-szeresére nő. T = 2 π a legkisebb pozitív periódus. Maximum keresése 2 π · k-ben; 3 2, k ∈ Z, minimumok π + 2 π · k-ben; - 3 2 , k ∈ Z .

Ha O x mentén felére tömörítjük, azt találjuk, hogy a legkisebb pozitív periódus a T = 2 π k 2 = π szám. Megtörténik a maximumok átmenete π · k-re; 3 2, k ∈ Z, minimumok - π 2 + π · k; - 3 2 , k ∈ Z .

Szimmetrikus leképezés Oy vonatkozásában. Mivel a grafikon páratlan, nem fog változni.

Ha a grafikont 1-gyel eltoljuk. A legkisebb pozitív periódusban T = π nincs változás. Maximum keresése π · k + 1-ben; 3 2, k ∈ Z, minimumok - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Ha 1-gyel eltoljuk, a legkisebb pozitív periódus egyenlő T = π és nem változik. Maximum keresése π · k + 1-ben; 5 2, k ∈ Z, minimumok π 2 + 1 + π · k-ben; - 1 2 , k ∈ Z .

A koszinuszfüggvény átalakítás befejeződött.
Tekintsük a transzformációkat az y = t g x példával.
6. példa
Szerkesszük meg az y = - 1 2 t g π 3 - 2 3 x + π 3 függvény gráfját az y = t g (x) függvény transzformációival.
Megoldás
Először is le kell redukálni az adott függvényt ± k 1 · f ± k 2 · x + a + b alakra, ami után megkapjuk, hogy
y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3
Jól látható, hogy k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, a k 1 és k 2 együtthatók előtt pedig egy „-”. Ez azt jelenti, hogy a tangenszoidok transzformációja után kapjuk
y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3
Érintők lépésről lépésre történő transzformációja grafikus ábrázolással.
Megvan, hogy az eredeti gráf y = t g (x) . A pozitív periódus változása egyenlő: T = π. A definíciós tartományt a következőnek tekintjük: - π 2 + π · k ; π 2 + π · k, k ∈ Z.
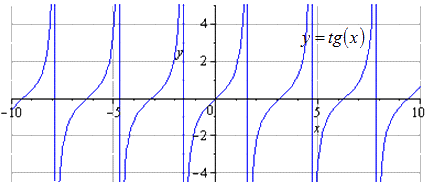
2-szer összenyomjuk az Oy mentén. T = π a legkisebb pozitív periódus, ahol a definíciós tartomány alakja - π 2 + π · k; π 2 + π · k, k ∈ Z.

Nyújtsa meg O x 3 mentén 2-szer. Számítsuk ki a legkisebb pozitív periódust, amely T = π k 2 = 3 2 π volt. A koordinátákkal rendelkező függvény definíciós tartománya pedig 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, csak a definíciós tartomány változik.

A szimmetria az O x oldalon megy. Az időszak ezen a ponton nem változik.

A koordinátatengelyeket szimmetrikusan kell megjeleníteni. A definíciós tartomány ebben az esetben változatlan. A menetrend egybeesik az előzővel. Ez arra utal, hogy az érintőfüggvény páratlan. Ha kell páratlan függvényállítsa be az O x és O y szimmetrikus leképezését, majd transzformálja az eredeti függvényre.

















