Szakaszok építése. Kutatómunka a "poliéderek metszeteinek felépítésének módszerei" témában

29.09.2019

Az előző feladatokban az elmélet ismerete elegendő volt a keresztmetszet elkészítéséhez. Nézzünk egy másik problémát. 1. feladat Szerkessze meg az M ponton átmenő tetraéder ABD síkkal párhuzamos szakaszát! M Egy pont nem segít rajtunk, de a problémának van egy további feltétele: a szakasznak párhuzamosnak kell lennie az ABD síkkal. Mit ad ez nekünk? 1. Az ADB és a DBC síkok a DB egyenes mentén metszik egymást, ezért az ADB-vel párhuzamos szakasz metszi a DBC-t mentén (Ha két párhuzamos egyenest a DB. síkkal párhuzamosan metsz egy harmadik, akkor a metszésvonalak párhuzamosak) M pont M pont tartozik hogy szembenézzen a DBC-vel. Rajzoljunk rajta N egy DB-vel párhuzamos MK egyenest. 2. Hasonlóan: (ADB) (ABC)=AB, K tehát a szakasz metszi (ABC) az AB-vel párhuzamos egyenesben. K(ABC). Az ABC síkban lévő K ponton keresztül húzz egy KN egyenest az AB-vel párhuzamosan. M N K N (ADC), M (ADC), ezért MN (ADC) (és vágási síkok). Végezzünk NM-et. Az MKN a kötelező szakasz. Tehát: M N 1. Konstrukció: 1. Síkban (DBC) MK // DB, MK BC = K. 2. Síkban (ABC) KN // AB, KN AC = N. 3. MN Bizonyítsuk be, hogy MKN a szükséges szakasz K 2. Bizonyítás. 1. A szakasz áthalad az M ponton 2. N (ADC), M (ADC) => NM (ADC) 3. MK // DB, NK // AB konstrukció szerint, ezért (NMK) // (ABD) tulajdonság. Ezért az MKN a b.t.c. kívánt szakasza. 2. feladat Szerkessze meg az ABCDA1B1C1D1 paralelepipedonnak a D1C1 él közepén és a D ponton átmenő, az a egyenessel párhuzamos szakaszát. B1 C1 Indoklás. M A1 D1 B A C D 1. Jelölje be a feltételben jelzett pontot (nevezzük tetszőlegesen). M – D1C1 közepe. 2. M és D pont B1 C1 M A1 A, ami azt jelenti, hogy összekapcsolhatók. D1 B C D ugyanabban a síkban DD1C1, Nincs több csatlakoztatnivaló. 3. Használjunk egy további feltételt: a vágási síknak párhuzamosnak kell lennie az a egyenessel. B1 C1 M A1 B C S A Ehhez az a vonallal párhuzamos egyenest kell tartalmaznia. A legegyszerűbb, ha az ABC síkban ilyen egyenest rajzolunk, mert szakaszhoz tartozó a egyenest és egy D pontot tartalmaz. D Az ABC síkban a D ponton keresztül húzzunk egy DS egyenest az a egyenessel párhuzamosan. DS AB = S. 4. Mivel (ABC) // (A1B1C1), rajzolja meg az (A1B1C1) síkot, az M ponton keresztül, az MP // SD egyenest. MP B1C1 = P 5. Mivel (DD1C1) // (AA1B1), akkor a P B C síkban (AA1B1) az S ponton keresztül DM-mel párhuzamos M N A D SN egyenest húzhatunk. SN BB1 = N 1 1 1 1 B C S A D 6. Az N és P pontok az (A1B1C1) síkban helyezkednek el. Kapcsoljuk össze őket. SNPMD - a szükséges szakasz. Tehát: 1. Építés. 1. MD B1 A1 N P C1 S A M 3. In (A1B1C1), az M ponton keresztül, MP // DS, MP B1C1 = P C 4. Az (AA1B1) síkban az S ponton át, SN // DM, SN BB1 = N 5. NP D1 B D 2. In (ABC), a D ponton át, DS // a, DS AB = S Bizonyítsuk be, hogy SNPMD a szükséges szakasz. 2. Bizonyítás. B1 A1 N 1. A metszet a D ponton és a D1C1 él közepén - M ponton halad át szerkesztéssel. P C1 M C S A 3. PM // SD, P B1C1 konstrukció szerint D1 B D 2. DS // a, (S AB) konstrukció szerint, ezért (KNP) // a attribútum szerint. 4. SN // DM, N BB1 konstrukció szerint 5. P (BB1C1), N (BB1C1) => PN (BB1C1). Ezért az SNPMD a kívánt keresztmetszet stb. 3. feladat Szerkesszünk meg egy párhuzamos, B1A-val párhuzamos, M és N pontokon áthaladó paralelepipedon szakaszt. Indoklás. 1. Kösse össze M és N (a (C1A1B1) síkban fekszenek). B1 N M A1 D1 B A C1 C D Nincs több kapcsolat. Használjunk egy további feltételt: a vágási síknak párhuzamosnak kell lennie a B1A 2 egyenessel. Ahhoz, hogy a vágási sík párhuzamos legyen az AB1-gyel, szükséges, hogy az AB1-gyel (vagy DC1-gyel, mivel DC // AB1-el párhuzamos egyenest tartalmazzon) a paralelepipedon tulajdonsága). A legkényelmesebb ilyen egyenes vonalat ábrázolni a DD1C1C arcban, mert (DD1C1) // (AA1B1) és AB1 (AA1B1). Rajzoljunk egy NK // AB1, NK DD1 = K egyenest a (DD1C1) síkban B1 N M A1 D1 B 3. Most az AA1D1 síkban van két pont, M és K, amelyek a szakaszhoz tartoznak. Kapcsoljuk össze őket. C K A C1 D MNK – a szükséges szakasz. Tehát: 1. Építés. 1. MN 2. Síkban (DD1C1) NK // AB1, NK DD1 = K. . B1 N A1 A M D1 C1 3. MK Bizonyítsuk be, hogy MNK a szükséges szakasz 2. Bizonyítás. B C 1. A szakasz áthalad az M és N pontokon. K 2. M (A1B1C1), N (A1B1C1) => D MN (A1B1C1). 3. M (ADD1), K (ADD1) => MK (ADD1). 4. Mert NK // AB1 szerkesztéssel, majd (MNK) // AB1 egyenes és sík párhuzamosságával. Ezért az MNK a kívánt szakasz a b.t.c. 3. feladat 1. A DABC tetraéderben alkossunk egy szakaszt a DC él közepén, a B csúcson átmenő és az AC egyenessel párhuzamos síkkal. 2. Szerkesszük meg a B1C1 él közepén és a CD élen fekvő K ponton átmenő síkkal a BD egyenessel párhuzamos paralelepipedon metszetét, ha DK: KC = 1: 3. M 3. Szerkesszünk egy tetraéder metszetet az M és C pontokon átmenő sík, amely párhuzamos a egyenessel (1. ábra). 1. ábra 4. Az ABCDA1B1C1D1 paralelepipedonban az E pont a CD élhez tartozik. Szerkesszük meg a paralelepipedon egy szakaszát ezen a ponton átmenő síkkal és párhuzamos a síkkal BC1D. 5. Szerkessze meg a paralelepipedonnak egy AA1-en átmenő, MN-nel párhuzamos síkot tartalmazó szakaszát, ahol M az AB felezőpontja, N a BC felezőpontja. 6. Szerkessze meg a paralelepipedon olyan metszetét, amelyik a B1C1 él közepén áthalad az AA1C1 síkkal párhuzamosan.

OKTATÁSI, TUDOMÁNYOS MINISZTÉRIUMÉS A KRÍMI KÖZTÁRSASÁG IFJÚSÁGA

KIS TUDOMÁNYOS AKADÉMIA "KERESŐ"

Tanszék: matematika

Szekció: matematika

MÓDSZEREK POLIÉDEK SZEKCIÓKÉPÍTÉSÉHEZ

Elvégeztem a munkát:

_______________

osztályos tanuló

Tudományos tanácsadó:

Absztraktok

Módszerek poliéderek metszete készítésére

Tanszék: matematika

Szekció: matematika

Tudományos tanácsadó:

A tanulmány célja az a poliéderek metszeteinek felépítésére szolgáló különféle módszerek tanulmányozása. Erre éselméleti anyagot tanulmányoztak ebben a témában, A szakaszok építési feladatainak megoldási módszereit rendszerezzük, példákat adunk az egyes módszerek alkalmazására vonatkozó problémákra, példákat adunk a szakaszok építése és elemeik kiszámítása egységes államvizsga problémáira.

BEVEZETÉS………………………………………………………………………………….3

1. SZAKASZ. A SZEREOMETRIA AXIÓMARENDSZER ALAPJÁN POLIÉDER METSZETEK KÉPÍTÉSE…………………………………………………………4

2. SZAKASZ. NYOMONDÁSI MÓDSZER POLIÉDEK SZAKCIÓK ÉPÍTÉSÉBEN…………………………………………………………………………………10

3. SZAKASZ. BELSŐ TERVEZÉSI MÓDSZER

POLIÉD SZEKCIÓK ÉPÍTÉSÉBEN………………………………………………

4. SZAKASZ. SZEKCIÓKÉPÍTÉSÉNEK KOMBINÁLT MÓDSZERE

POLYéder……………………………………………………………17

5. SZAKASZ. KOORDINÁCIÓS MÓDSZER POLYÉDEK SZEKCIÓKÉPÍTÉSÉHEZ………………………………………………………………………………….19

KÖVETKEZTETÉS………………………………………………………………25

IRODALOM………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

BEVEZETÉS

A végzősöknek matematikából kell vizsgát tenniük, valamint a sztereometrikus problémák megoldásának ismerete és képessége szükséges ahhoz, megírni ezt a vizsgátmaximális pontszámot. Relevancia Ez a munka magában foglalja a vizsgára való önálló felkészülés szükségességét, és a vizsgált téma az egyik legfontosabb.

A demó elemzése, diagnosztika és képzés Egységes államvizsga lehetőségek Val vel 2009-2014 megmutatta, hogy 70% A geometriai feladatok metszetkészítési és elemszámítási feladatokból állnak– szögek, területek.

BAN BEN tanterv poliéder szakaszok megalkotásával kapcsolatos feladatokat osztják ki 2 akadémiai órákat, ami nem elég a téma tanulmányozásához. Az iskolában a poliéderek síkmetszete csak a sztereometria axiómái és tételei alapján készül. Ugyanakkor vannak más módszerek is a poliéderek sík szakaszainak megalkotására. A leghatékonyabb a nyomkövetési módszer, a belső tervezési módszer és a kombinált módszer. Nagyon érdekes és ígéretes a megoldáshoz való alkalmazás szempontjából különféle feladatokat koordináta módszer. Ha a poliédert koordinátarendszerbe helyezzük, és a vágási síkot egy egyenlettel adjuk meg, akkor a metszet megalkotása a sík és a poliéder éleinek metszéspontjainak koordinátáinak megkeresésére redukálódik.

Tanulmányi tárgy: poliéderek metszete készítésének módszerei.

A tanulmány célja: tanulmány különféle módszerek poliéder szakaszok építése.

Kutatási célok:

1) Tanulmányozzon elméleti anyagot ebben a témában.

2) Rendszerezze a szakaszok építési problémáinak megoldási módszereit.

3) Mondjon példákat feladatokra az egyes módszerek használatához!

4) Tekintsen példákat az Egységes Államvizsga problémáira a szakaszok felépítésével és elemeinek kiszámításával kapcsolatban.

1. SZAKASZ

POLYÉDER SZEKCIÓKÉPÍTÉSE

A SZEREOMETRIA AXIÓMARENDSZERÉN ALAPJÁN

Meghatározás. A poliéder sík szerinti szakaszát ún geometriai alakzat, amely a tér összes olyan pontjának halmaza, amely egyidejűleg egy adott poliéderhez és síkhoz tartozik; a síkot vágósíknak nevezzük.

A poliéder felülete élekből - szegmensekből és lapokból - lapos sokszögekből áll. Mivel egy egyenes és egy sík egy pontban metszi egymást, két sík pedig egy egyenes mentén metszi egymást, ezért a poliéder síkmetszete sík sokszög; ennek a sokszögnek a csúcsai a vágási sík és a poliéder éleinek metszéspontjai, az oldalai pedig azok a szakaszok, amelyek mentén a vágósík metszi a lapjait. Ez azt jelenti, hogy egy adott poliéder kívánt szakaszát α síkkal kell megszerkeszteni elég megszerkeszteni a poliéder éleivel való metszéspontjait. Ezután kösse össze ezeket a pontokat egymás után szegmensekkel.

Az α vágási síkot a következőkkel adhatjuk meg: három pont, amelyek nem ugyanazon az egyenesen helyezkednek el; egy egyenes és egy nem hozzá tartozó pont; egyéb feltételek, amelyek meghatározzák a helyzetét egy adott poliéderhez képest. Például az 1. ábrán a PABCD négyszöggúla egy metszetét az M, K és H pontok által meghatározott α sík alkotja, amelyek a PC, PD és PB élekhez tartoznak;

1. ábra

Feladat. A paralelcső ABC-ben DA 1 B 1 C 1 D 1 szakaszt készíteni síkon, áthaladva a csúcsokon C és D 1, valamint a B 1 C 1 szakasz K pontja (2. ábra, a).

Megoldás. 1. T. Nak nek . VAL VEL ∈ DD 1 C 1, D 1 ∈ DD 1 C 1, majd az axióma szerint (két ponton keresztül, a repülőhöz tartozó, egyenes vonalon halad át, és csak egy) konstruáljuk meg a CD 1 nyomkövetést a DD 1 C 1 síkban (2. ábra, b).

2. Hasonlóan az A síkban 1 B 1 C 1 DK nyomvonalat, BB 1 C 1 síkban pedig CK nyomot szerkesztünk.

3. D 1 KC – a kívánt szakaszt (ábra..2, c)

a B C)

2. ábra

Feladat. Szerkesszük meg az RABC piramis α = (MKH) síkú metszetét, ahol M, K és H az RS, PB és AB élek belső pontjai (3. ábra, a).

Megoldás. 1. lépés. Az M és K pont a két α és RVS síkban található. Ezért a két sík metszésponti axiómája szerint az α sík az MK egyenes mentén metszi az RVS síkot. Következésképpen az MK szegmens a kívánt szakasz egyik oldala (3. ábra, b).

2. lépés. Hasonlóképpen a KN szegmens a kívánt szakasz másik oldala (3. ábra, c).

3. lépés. Az M és H pontok nem fekszenek egyszerre az RABC piramis egyik lapján sem, ezért az MH szakasz nem a gúla metszetének oldala. A KN és RA egyenesek az AVR lapjának síkjában fekszenek és metszik egymást. Szerkesszük meg a T= KH ∩AP pontot (3. ábra, d).

Mivel a KN egyenes az α síkban van, így a T pont az α síkban van. Most látjuk, hogy az α síkok és APC-nek közös pontja van M és T. Következésképpen két sík metszéspontjának axiómája szerint az α sík és az APC sík az MT egyenes mentén metszi egymást, ami viszont az R pontban metszi az AC élt (3. ábra, e). .

4. lépés. Most, az 1. lépéshez hasonlóan, megállapítjuk, hogy az α sík metszi az ACP és ABC lapokat az MR és HR szakaszok mentén. Következésképpen a szükséges szakasz az MKHR négyszög (3. ábra, f).

3. ábra

Nézzünk egy összetettebb problémát.

Feladat . Szerkesszük meg a PABCDE ötszögletű piramis metszetét síkon

α = (KQR), ahol K, Q az RA és RS élek belső pontjai, az R pont pedig a DPE felületen belül van (4. ábra, a).

Megoldás . A QK és AC egyenesek ugyanabban az ACP síkban fekszenek (egy egyenes és egy sík axiómája szerint), és egy T pontban metszik egymást. 1 , (4. ábra,b), míg a T 1 є α, mivel QК є α.

A PR egyenes egy F pontban metszi a DE-t (4. ábra, c), amely az ARR sík és a gúla alapjának DE oldala metszéspontja. Ekkor a KR és AF egyenesek ugyanabban az ARR síkban fekszenek, és egy T pontban metszik egymást 2 (4. ábra d), míg a T 2 є α , mint a KR є α egyenes pontja (az egyenes és a sík axiómája szerint).

Érkezett: egyenes T 1 T 2 az α szekáns síkban és a gúla alapjának síkjában fekszik (az egyenes és a sík axiómája szerint), míg az egyenes metszi a gúla ABCDE alapjának DE és AE oldalait, az M és N pontokban (4. ábra, e), amelyek az α sík metszéspontjai a gúla DE és AE éleivel, és a kívánt szakasz csúcsaiként szolgálnak.

Továbbá az MR egyenes a DPE homlok síkjában és az α vágási síkban fekszik (egy egyenes és egy sík axiómája szerint), miközben metszi a PD élt egy H pontban - a kívánt szakasz másik csúcsa. (4. ábra, f).

Ezután építsük fel a T pontot 3 - T 1 T 2 ∩ AB (4. ábra, g), amely a T egyenes pontjaként 1 T 2 є α, az a síkban fekszik (az egyenes és a sík axiómája szerint). Most a RAB arc síkja két T ponthoz tartozik 3 és Az α vágósíkra, ami a T egyenest jelenti 3 K e síkok metszésvonala. Egyenes T 3 K metszi a PB élt az L pontban (4. ábra, h), amely a kívánt szakasz következő csúcsaként szolgál.

Így a kívánt szakasz felépítéséhez szükséges sorozat „lánca” a következő:

1. T 1 = QK∩ AC ; 2. F = PR ∩ DE;

3. T 2 = KR ∩ AF; 4. M = T 1 T 2 ∩ DE;

5.N= T 1 T 2 ∩ AE ; 6. N = MR ∩ PD;

7. T 3 = T 1 T 2 ∩ AB ; 8.L=T 3 K ∩ PB.

Hatszög MNKLQH a szükséges szakasz.

4. ábra

A párhuzamos síkok tulajdonságait felhasználva megszerkeszthető egy poliéder párhuzamos lapjaival (prizma, paralelepipedon kocka) egy metszet.

Feladat . Az M, P és R pontok a paralelepipedon élein helyezkednek el. A párhuzamos egyenesek és síkok tulajdonságait felhasználva készítse el ennek a paralelepipedonnak az MPR sík általi metszetét.

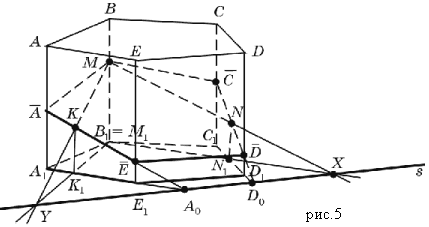
Megoldás. Legyenek M, P és R pontok rendre a DD élein 1, BB 1 és SS 1 paralelepipedon ABCBA 1 B 1 C 1 B 1 (5. ábra, a).

Jelöljük: (MPR) = α - vágási sík. Rajzolunk MR és PR szakaszokat (5. ábra, b), amelyek mentén az α sík metszi a CC lapokat, ill. 1 D 1 D és BB 1 C 1 Ebből a paralelepipedonból. Az MR és PR szegmensek a kívánt szakasz oldalai. Ezután két párhuzamos sík és egy harmadik metszéspontjára vonatkozó tételeket használunk.

Mivel az AA arc 1 B 1 B párhuzamos a CC felülettel 1 D 1 D, majd az α sík és az AA lap síkjának metszésvonala 1 az 1-ben B-nek párhuzamosnak kell lennie az MR egyenessel. Ezért megrajzoljuk a PQ || szakaszt MR, Q є AB (5. ábra, c); A PQ szegmens a kívánt szakasz következő oldala. Hasonlóképpen, mivel arc AA 1 D 1 D párhuzamos a CC felülettel 1 az 1-ben B, majd az α sík és az AA lap síkjának metszésvonala 1 D 1 D párhuzamosnak kell lennie a PR egyenessel. Ezért megrajzoljuk az MH || szakaszt PR, H = AD (5. ábra, c); Az MH szegmens a kívánt szakasz másik oldala. Az ABCD lap AB és AD éleire Q є AB és H є AD pontokat építettünk, amelyek a kívánt szakasz csúcsai. Megrajzoljuk a QH szakaszt, és megkapjuk az MRPQH ötszöget - a paralelepipedon kívánt szakaszát.

a B C)

Rizs. 5

2. SZAKASZ

NYOMONDÁSI MÓDSZER POLYÉDER SZEKCIÓK ÉPÍTÉSÉBEN

Meghatározás. Azt az egyenest, amely mentén az α vágósík metszi a poliéder alapsíkját, az α sík nyomvonalának nevezzük ezen alap síkjában.

A nyom definíciójából azt kapjuk, hogy minden pontjában egyenesek metszik egymást, amelyek közül az egyik a metsző, a másik az alap síkjában fekszik. A nyomkövetésnek ezt a tulajdonságát használjuk a poliéderek síkmetszete nyomkövetési módszerrel történő megalkotásakor. Ebben az esetben a vágási síkban célszerű egyenes vonalakat használni, amelyek metszik a poliéder széleit.

Először a hasítósíkot a prizma alapjának síkjában (gúla) és a prizma felületéhez tartozó ponttal (gúla) definiáljuk.

Feladat. Szerkessze meg az ABCVEA prizma keresztmetszetét 1 B 1 C 1 D 1 E 1 α sík, amelyet a következők adnak megl a prizma alapjának ABC síkjában és a DD élhez tartozó M pontban 1 (7. ábra, a).

Megoldás. Elemzés. Tegyük fel, hogy az MNPQR ötszög a kívánt szakasz (6. ábra). Ennek a lapos ötszögnek az elkészítéséhez elegendő megszerkeszteni az N, P, Q, R csúcsait (az M pont adott) - az α vágósík metszéspontjait az élekkel, ill. 1, BB 1, AA 1, EE 1 ebből a prizmából.

Rizs. 6

Az N = α ∩ СС pont megalkotásához 1 elég megszerkeszteni az α vágósík metszésvonalát a СDD lap síkjával 1 C 1 . Ehhez viszont elég ennek a lapnak a síkjában egy másik, az α vágási síkhoz tartozó pontot megszerkeszteni. Hogyan lehet egy ilyen pontot felépíteni?

Mivel egyenes l a prizma alapjának síkjában fekszik, akkor metszheti a CDD lap síkját 1 C 1 csak azon a ponton, amely a CD = (CDD 1 ) ∩ (ABC), azaz. X pont =l∩CD = l∩ (CDD 1 ) az α vágási síkhoz tartozik. Így az N = α ∩ СС pont megszerkesztéséhez 1 elég az X = pontot megszerkesztenil ∩CD. Hasonlóképpen P = α ∩ BB pontok megalkotásához 1, Q = α ∩ AA 1 és R = α ∩ EE 1 elég a pontokat ennek megfelelően megszerkeszteni: Y =l∩ BC, Z = l∩ AB és T = l∩ AE. Innen

Építkezés.

X = l∩ CD (7. ábra, b);

N = MX ∩ СС 1 (7. ábra, b);

Y = l∩ BC (7. ábra, c);

P = NY ∩ BB 1 (7. ábra, c);

Z= l∩ AB (7. ábra, c);

Q= PZ ∩ AA 1 (7. ábra, d);

T= l∩ AE (6. ábra);

R= QT ∩ EE 1 (6. ábra).

Pentagon MNPQR a szükséges szakasz (6. ábra).

Bizonyíték . Mivel egyenes l az α vágási sík nyoma, akkor az X = pontokl∩ СD, Y = l∩ BC, Z = l∩ AB és T= l ∩ AE ehhez a síkhoz tartozik.

Ezért rendelkezünk:

М є α , X є α => МХ є α, majd МХ ∩ СС 1 = N є α, ami azt jelenti, hogy N = α ∩ СС 1 ;

N є α, Y є α => NY є α, majd NY ∩ ВВ 1 = Р є α, ami azt jelenti, hogy Р = α ∩ ВВ 1 ;

Р є α, Z є α => РZ є α, majd PZ ∩ AA 1 = Q є α, ami azt jelenti, hogy Q = α ∩ AA 1 ;

Q є α, T є α => QТ є α, majd QТ ∩ EE 1 =R є α, ami azt jelenti, hogy R = α ∩ Е 1 .

Ezért az MNPQR a szükséges szakasz.

a) b)

c) d)

Rizs. 7

Tanulmány. Nyomon követni l α vágósík nem metszi a prizma alapját, és a vágási sík M pontja a DD oldalélhez tartozik 1 prizmák. Ezért az α vágási sík nem párhuzamos az oldalélekkel. Következésképpen az N, P, Q és R pontok, amelyek ennek a síknak a prizma oldaléleivel (illetve ezen élek kiterjesztésével) metszik, mindig léteznek. És mivel ráadásul az M pont nem tartozik a nyomhozl , akkor az általuk meghatározott α sík egyedi. Ez azt jelenti, hogy a problémának egyedi megoldása van.

Feladat. Szerkesszük meg a PABCDE ötszögletű piramis metszetét a következő sík segítségével!l és a PE él K belső pontja.

Megoldás. Sematikusan a kívánt szakasz felépítése a következőképpen ábrázolható (8. ábra): T 1 → Q → T 2 → R → T 3 → M → T 4 → N.

A Pentagon MNKQR a szükséges szakasz.

A szakasz csúcsainak felépítési sorrendjének „lánca” a következő:

1. T 1 = l∩ AE; 2. Q = T 1 K ∩ RA;

3. T 2 = l∩ AB; 4. R = T 2 Q ∩ РВ;

5. T 3 = l∩ BC; 6. M = T 3 R ∩ RS;

7. T 4 = l∩CD; 8. N = T 4 M ∩ РD.

Rizs. 8

A vágási síkot gyakran három, a poliéderhez tartozó pont határozza meg. Ebben az esetben a kívánt szakasz nyomkövetési módszerrel történő megszerkesztéséhez először az adott poliéder alapjának síkjában készítsük el a vágási sík nyomát.

3. SZAKASZ

BELSŐ TERVEZÉSI MÓDSZER

POLIÖÉDER METSZETEK ÉPÍTÉSÉBEN

A belső tervezési módszert korrespondencia módszernek, vagy átlós metszetek módszerének is nevezik.

A módszer alkalmazásakor minden adott pont az alapsíkra vetítésre kerül. Van két lehetséges típusok kialakítás: központi és párhuzamos. A központi vetítést általában piramisszakaszok készítésekor használják, ahol a piramis teteje a vetület középpontja. A párhuzamos tervezést a prizma szakaszainak építésénél alkalmazzák.

Feladat . Szerkesszük meg a PABCDE piramis α = (MFR) síkú metszetét, ha az M, F és R pontok az RA, RS és PE élek belső pontjai (9. ábra, a).

Megoldás . Jelöljük a piramis alapsíkját β-val. A kívánt szakasz megszerkesztéséhez megszerkesztjük az α vágósík metszéspontjait a gúla éleivel.

Szerkesszük meg a vágósík metszéspontját ennek a piramisnak a PD élével.

Az APD és CPE síkok metszik a β síkot az AD és CE egyenesek mentén, amelyek egy K pontban metszik egymást (9. ábra, c). A PK=(APD) ∩(CPE) egyenes metszi az FR є α egyenest egy K pontban 1-től 1-ig = RK ∩ FR (9. ábra, d), míg K 1 є α. Akkor: M є α, K 1 є α => egyenes MK є a. Ezért Q pont = MK 1 ∩ PD (9. ábra, e) a PD él és a vágási sík metszéspontja: Q = α ∩ PD. A Q pont a kívánt szakasz csúcsa. Hasonlóképpen megszerkesztjük az α sík és a PB él metszéspontját. A BPE és АD síkok metszik a β síkot a BE és AD egyenesek mentén, amelyek a H pontban metszik egymást (9. ábra, e). Egyenes PH = (BPE) ∩ (APD) metszi az MQ egyenest a H pontban 1 (9. ábra, g). Ezután az RN egyenes 1 metszi a PB élt az N = α ∩ PB pontban - a szakasz csúcsa (9. ábra, h).

1. K = AD ∩ EC; 2. K 1 = RK ∩ RF;

3.Q= MK 1 ∩ R D; 4. H = BE ∩ A D;

5. Н 1 = РН ∩ МQ; 6. N = RН 1 ∩ РВ.

Pentagon MNFQR a szükséges szakasz (9. ábra, i).

a B C)

Ahol)

g) h) i)

Rizs. 9

Feladat . Szerkesszük meg az ABCDEA prizma keresztmetszetét! 1 B 1 C 1 D 1 E 1 , α sík, az M є BB pontok által meghatározott 1, P DD 1, Q EE 1 (10. ábra).

Megoldás. Jelöljük: β - a prizma alsó bázisának síkja. A kívánt szakasz megszerkesztéséhez megszerkesztjük az α = (MPQ) sík és a prizma éleinek metszéspontjait.

Szerkesszük meg az α sík és az AA él metszéspontját 1 .

Síkok A 1 AD és BEE 1 metszi a β síkot az AD és BE egyenesek mentén, amelyek egy K pontban metszik egymást. Mivel az A síkok 1 AD és MÉH 1 átmennek az AA párhuzamos éleken 1 és BB 1 prizmák és van egy közös K pontjuk, majd a KK egyenes 1 metszéspontjuk átmegy a K ponton és párhuzamos a BB éllel 1 . Jelöljük ennek az egyenesnek a metszéspontját a QM egyenessel: K 1 = KK 1 ∩ QM, KK 1 ║ BB 1 . Mivel QM є α, akkor K 1 є α.

Rizs. 10

Érkezett: Р є α, K 1 є α => egyenes RK 1 є α, míg RK 1 ∩ AA 1 = R. Az R pont az α sík és az AA él metszéspontjaként szolgál 1 (R = α ∩ AA 1 ), ezért a kívánt szakasz csúcsa. Hasonlóképpen megszerkesztjük az N = α ∩ СС pontot 1 .

Így a kívánt szakasz felépítéséhez szükséges „lépések” sorrendje a következő:

K = AD ∩ BE; 2. K 1 = KK 1 ∩ MQ, KK 1 || BB 1;

R = RK 1 ∩ AA 1 ; 4. H = EC ∩AD;

H 1 – HH 1 ∩ РR, НН 1 || CC 1; 6.N = QН 1 ∩ СС 1.

A Pentagon MNPQR a szükséges szakasz.

Ebben a leckében megnézzük a tetraédert és elemeit (tetraéder éle, felülete, lapjai, csúcsai). És számos problémát megoldunk a tetraéder metszeteinek felépítésével kapcsolatban általános módszer szakaszok építéséhez.

Téma: Egyenesek és síkok párhuzamossága

Tanulság: Tetraéder. Problémák a tetraéder metszeteinek felépítésénél

Hogyan építsünk tetraédert? Vegyünk egy tetszőleges háromszöget ABC. Bármilyen pont D, amely nem ennek a háromszögnek a síkjában fekszik. 4 háromszöget kapunk. A négy háromszög által alkotott felületet tetraédernek nevezzük (1. ábra). Az e felület által határolt belső pontok is a tetraéder részét képezik.

Rizs. 1. ABCD tetraéder

A tetraéder elemei
A,B, C, D - tetraéder csúcsai.
AB, A.C., HIRDETÉS, IDŐSZÁMÍTÁSUNK ELŐTT., BD, CD - tetraéder élek.
ABC, ABD, BDC, ADC - tetraéderlapok.

Megjegyzés: laposra vihető ABC mögött tetraéder bázis, majd pont D van tetraéder csúcsa. A tetraéder minden éle két sík metszéspontja. Például borda AB- ez a síkok metszéspontja ABDÉs ABC. A tetraéder minden csúcsa három sík metszéspontja. Csúcs A síkokban fekszik ABC, ABD, ADVAL VEL. Pont A a három kijelölt sík metszéspontja. Ez a tény a következőképpen van leírva: A= ABC ∩ ABD ∩ ACD.

Tetraéder meghatározása

Így, tetraéder négy háromszög alkotta felület.

Tetraéder él- a tetraéder két síkjának metszésvonala.

6 gyufából készíts 4 egyenlő háromszöget! Repülőgépen lehetetlen megoldani a problémát. És ezt könnyű megtenni az űrben. Vegyünk egy tetraédert. 6 gyufa az élei, a tetraéder négy lapja, és négy egyenlő háromszög lesz. A probléma megoldódott.

Adott egy tetraéder ABCD. Pont M a tetraéder egyik széléhez tartozik AB, pont N a tetraéder egyik széléhez tartozik BAN BENDés időszak Réléhez tartozik DVAL VEL(2. ábra). Szerkesszük meg a tetraéder metszetét egy síkkal MNP.

Rizs. 2. Rajz a 2. feladathoz - Készítsen egy tetraéder metszetét síkkal

Megoldás:
Tekintsük egy tetraéder lapját DNap. A lényeg ezen az oldalán NÉs P az arcokhoz tartoznak DNap, és ezért a tetraéder. De a pont állapota szerint N, P a vágási síkhoz tartoznak. Eszközök, NP- ez két sík metszésvonala: az arc síkja DNapés vágósík. Tegyük fel, hogy egyenesek NPÉs Nap nem párhuzamos. Ugyanabban a síkban fekszenek DNap. Keressük meg az egyenesek metszéspontját NPÉs Nap. Jelöljük E(3. ábra).

Rizs. 3. Rajz a 2. feladathoz. E pont megkeresése

Pont E metszetsíkhoz tartozik MNP, mivel a vonalon fekszik NP, és az egyenes NP teljes egészében a metszetsíkban fekszik MNP.

Szintén pont E síkban fekszik ABC, mert egyenesen fekszik Nap repülőn kívül ABC.

Ezt értjük ESZIK- síkok metszésvonala ABCÉs MNP, pont óta EÉs M egyszerre két síkban feküdni - ABCÉs MNP. Kössük össze a pontokat MÉs E, és folytassa egyenesen ESZIK a vonal kereszteződéséig AC. A vonalak metszéspontja ESZIKÉs AC jelöljük K.

Tehát ebben az esetben NPQМ- a szükséges szakaszt.

Rizs. 4. Rajz a 2. feladathoz. A 2. feladat megoldása

Nézzük most azt az esetet, amikor NP párhuzamos IDŐSZÁMÍTÁSUNK ELŐTT.. Ha egyenes NP párhuzamos valamilyen egyenessel, például egy egyenessel Nap repülőn kívül ABC, majd egyenesen NP párhuzamos a teljes síkkal ABC.

A kívánt metszetsík átmegy az egyenesen NP, párhuzamos a síkkal ABC, és egyenes vonalban metszi a síkot MQ. Tehát a metszésvonal MQ párhuzamos a vonallal NP. Kapunk NPQМ- a szükséges szakaszt.

Pont M oldalán fekszik ADBAN BEN tetraéder ABCD. Szerkesszük meg a tetraéder egy szakaszát a ponton átmenő síkkal M párhuzamos az alappal ABC.

Rizs. 5. Rajz a 3. feladathoz Szerkesszen meg egy tetraéder metszetét síkkal!

Megoldás:
Vágó sík φ párhuzamos a síkkal ABC a feltétel szerint ez azt jelenti, hogy ez a sík φ párhuzamos vonalakkal AB, AC, Nap.
Repülőn ABD ponton keresztül M csináljunk közvetlen PQ párhuzamos AB(5. ábra). Egyenes PQ síkban fekszik ABD. Hasonlóan a síkban ACD ponton keresztül R csináljunk közvetlen PR párhuzamos AC. Van egy pont R. Két egymást metsző vonal PQÉs PR repülőgép PQR rendre párhuzamos két egymást metsző egyenessel ABÉs AC repülőgép ABC, ami repülőket jelent ABCÉs PQR párhuzamos. PQR- a szükséges szakaszt. A probléma megoldódott.

Adott egy tetraéder ABCD. Pont M- belső pont, pont a tetraéder lapján ABD. N- a szakasz belső pontja DVAL VEL(6. ábra). Szerkessze meg egy egyenes metszéspontját N.M.és repülőgépek ABC.

Rizs. 6. Rajz a 4. feladathoz

Megoldás:
Ennek megoldására készítünk egy segédsíkot DMN. Legyen egyenes DM pontban metszi az AB egyenest NAK NEK(7. ábra). Akkor, SKD- ez a sík egy része DMNés tetraéder. Repülőn DMN hazugság és egyenes N.M., és a kapott egyenes SK. Tehát, ha N.M. nem párhuzamos SK, akkor valamikor keresztezik egymást R. Pont Rés ott lesz a vonal kívánt metszéspontja N.M.és repülőgépek ABC.

Rizs. 7. Rajz a 4. feladathoz. A 4. feladat megoldása

Adott egy tetraéder ABCD. M- az arc belső pontja ABD. R- az arc belső pontja ABC. N- az él belső pontja DVAL VEL(8. ábra). Szerkesszünk meg egy tetraéder metszetét a pontokon átmenő síkkal! M, NÉs R.

Rizs. 8. Rajz az 5. feladathoz Szerkesszen meg egy tetraéder metszetét síkkal!

Megoldás:
Tekintsük az első esetet, amikor az egyenes MN nem párhuzamos a síkkal ABC. Az előző feladatban megtaláltuk az egyenes metszéspontját MNés repülőgépek ABC. Ez a lényeg NAK NEK, azt a segédsík segítségével kapjuk meg DMN, azaz mi igen DMés pontot kapunk F. végzünk CFés a kereszteződésben MN pontot kapunk NAK NEK.

Rizs. 9. Rajz az 5. feladathoz. A K pont megtalálása

Csináljunk direkt KR. Egyenes KR a metszetsíkban és a síkban egyaránt fekszik ABC. A pontok megszerzése P 1És R 2. Csatlakozás P 1És Més folytatásként megkapjuk a lényeget M 1. A pont összekapcsolása R 2És N. Ennek eredményeként megkapjuk a kívánt szakaszt Р 1 Р 2 NM 1. Az első esetben a probléma megoldódott.
Tekintsük a második esetet, amikor az egyenes MN párhuzamos a síkkal ABC. Repülőgép MNP egyenes vonalon halad át MN párhuzamos a síkkal ABCés metszi a síkot ABC valamilyen egyenes mentén R 1 R 2, majd egyenesen R 1 R 2 párhuzamos az adott egyenessel MN(10. ábra).

Rizs. 10. Rajz az 5. feladathoz. A szükséges szakasz

Most húzzunk egy egyenest R 1 Més pontot kapunk M 1.Р 1 Р 2 NM 1- a szükséges szakaszt.

Szóval, megnéztük a tetraédert, megoldottunk néhányat tipikus feladatok tetraéderhez. A következő leckében egy paralelepipedont nézünk meg.

1. I. M. Szmirnova, V. A. Szmirnov. - 5. kiadás, javítva és bővítve - M.: Mnemosyne, 2008. - 288 p. : ill. Geometria. 10-11. osztály: tankönyv tanulóknak oktatási intézmények(alap és profilszint)

2. Sharygin I.F. - M.: Túzok, 1999. - 208 p.: ill. Geometria. 10-11. évfolyam: Tankönyv általános oktatási intézmények számára

3. E. V. Potoskuev, L. I. Zvalich. - 6. kiadás, sztereotípia. - M.: Túzok, 008. - 233 p. :il. Geometria. 10. évfolyam: Tankönyv általános oktatási intézmények számára a matematika elmélyült és szakirányú tanulmányozásával

További webes források

2. Hogyan készítsünk egy tetraéder keresztmetszetét. Matematika ().

3. Fesztivál pedagógiai elképzelések ().

Otthoni feladatok megoldása a „Tetraéder” témában, hogyan találjuk meg a tetraéder élét, a tetraéder lapjait, a tetraéder csúcsait és felületét

1. Geometria. 10-11. évfolyam: tankönyv általános oktatási intézmények tanulói számára (alap- és szakirányú szint) I. M. Smirnova, V. A. Smirnov. - 5. kiadás, javítva és bővítve - M.: Mnemosyne, 2008. - 288 p.: ill. 18., 19., 20. feladatok 50. o

2. Pont E középső erezet MA tetraéder MAVS. Szerkesszük meg a tetraéder szakaszát a pontokon átmenő síkkal! IDŐSZÁMÍTÁSUNK ELŐTTÉs E.

3. A MABC tetraéderben az M pont az AMV laphoz, a P pont a BMC laphoz, a K pont az AC élhez tartozik. Szerkesszük meg a tetraéder szakaszát a pontokon átmenő síkkal! M, R, K.

4. Milyen alakzatokat kaphatunk a tetraéder és a sík metszéspontja eredményeként?

A munka célja:
Térfogalmak fejlesztése.
Feladatok:
1. Ismertesse meg a szakaszok kialakításának szabályait!
2. Fejleszteni kell a szakaszok építési készségeit
tetraéder és paralelepipedon különböző
vágási sík megadásának esetei.
3. Szabályalkalmazási képesség fejlesztése
szakaszok építése a problémák megoldása során
témák "Poliéderek".

Sok megoldására
geometriai
szükséges feladatokat
szakaszokat építeni
poliéder
különféle
repülőgépek.

A vágósík fogalma

Metsző
repülőgép
paralelepipedon
(tetraéder)
bármelyiknek hívják
síkban, mindkét oldalon
oldalairól
amely
adott pontok
paralelepipedon
(tetraéder).

A poliéder szakasz fogalma

Vágó sík
keresztezi az éleket
tetraéder
(párhuzamos) által
szegmensek.
Sokszög, oldalak
melyik adat
szegmenseket nevezzük
tetraéder keresztmetszete
(paralelepipedon).

Rajzokból való munka

Hány síkot lehet megrajzolni
kiválasztott elemeken keresztül?
Milyen axiómákat és tételeket alkalmazott?

Szakasz felépítéséhez
pontokat kell ábrázolnia
szekáns kereszteződés
síkok élekkel és
szegmensekkel köti össze őket.

A szakaszok kialakításának szabályai

1. Csak kettőt köthet össze
pontok síkjában egy
élek.
2. A vágási sík metszi egymást
párhuzamos lapok mentén
párhuzamos szegmensek.

A szakaszok kialakításának szabályai

3. Ha az arc síkja ki van jelölve
csak egy pont tartozik hozzá
metszetsík, akkor szükséges
építeni egy további pontot.
Ehhez meg kell találni a pontokat
már megépült kereszteződései
egyenes vonalak más egyenesekkel,
ugyanazokon a széleken hever.

10. Tetraéderszelvények felépítése

11.

A tetraédernek 4 lapja van
Szakaszokban kiderülhet
Háromszögek
Négyszögek

12.

Szerkesszük meg a tetraéder keresztmetszetét!
DABC sík elhalad
M,N,K pontokon keresztül
1. Rajzoljunk át egy egyenest
pont M és K, mert hazudnak
az egyik oldalon (ADC).
D
M
A.A.
N
K
BB
CC
2. Rajzoljunk át egy egyenest
pont K és N, mert Ők
ugyanazon az oldalon feküdni
(CDB).
3. Hasonlóan érvelve,
húzz egy egyenest MN.
4. Háromszög MNK –
a kívánt szakaszt.

13. áthaladva az M ponton az ABC-vel párhuzamosan.

D
1. Rajzoljunk át az M ponton
egyenes párhuzamos
AB él
2.
M
R
A
NAK NEK
VAL VEL
BAN BEN
Menjünk át az M ponton
egyenes párhuzamos
él AC
3. Rajzoljunk át egy egyenest
pont K és P, mert belefekszenek
egy arc (DBC)
4. Háromszög MPK –
a kívánt szakaszt.

14.

Egy tetraéder metszetének megszerkesztése síkkal,
áthaladva az E, F, K pontokon.
D
1. KF-et végzünk.
2. FE-t végzünk.
3. Folytassuk
EF, folytassuk az AC-t.
F
4.EF AC =M
5. Végrehajtjuk
MK.
E
M
AB=L
6.
MK
C
A
7. EL
L
EFKL – kötelező szakasz
K
B

15.

Egy tetraéder metszetének megszerkesztése síkkal,
áthaladva az E, F, K pontokon
Melyikek
amit egyenesen
pont,
fekve
Tud
Csatlakozás
a keletkező
Melyik
pontokat
Tud
azonnal
hogy
vagy
élek
Tud
folytatni,
nak nek
kap
pontok,
fekvő
V
egy
csatlakozni?
csatlakozni
kapott
további
pont?
élek,
név
szakasz.
plusz pont?
D
AC
ELFK
FSEC
és egy pont
K és E
és FK
F
L
C
M
A
E
K
B

16.

Építsen egy szakaszt
tetraéder sík,
pontokon áthaladva
E, F, K.
D
F
L
C
A
E
K
B
RÓL RŐL

17.

Következtetés: a módszertől függetlenül
építési szakaszok azonosak

18. Parallepipedon szakaszok építése

19.

A tetraédernek 6 lapja van
Háromszögek
Ötszögek
A szakaszaiban kiderülhet
Négyszögek
Hatszögek

20. Szerkessze meg a paralelepipedon metszetét, amelynek az X ponton átmenő síkja párhuzamos a síkkal (OSV)

AZ 1-BEN
A1
Y
x
D1
S
BAN BEN
A
D
Z
1. Végigvezetjük
C1
pont X egyenes
párhuzamos a szélével
D1C1
2. X ponton keresztül
közvetlen
párhuzamos a szélével
D1D
3. A Z ponton keresztül van egy egyenes
párhuzamos a szélével
VAL VEL
DC
4. Rajzoljunk át egy egyenest
pont S és Y, mert belefekszenek
egy arc (BB1C1)
XYSZ – kötelező szakasz

21.

Építsd meg a paralelepipedon metszetét
pontokon áthaladó sík
ŐRÜLT
AZ 1-BEN
D1
E
A1
C1
BAN BEN
A
1. Kr. u
2. MD
3. ÉN//HIRDETÉS, mert (ABC)//(A1B1C1)
4. A.E.
5. AEMD – kötelező szakasz
M
D
VAL VEL

22. Szerkessze meg a paralelepipedon M, K, T pontokon átmenő sík szakaszát!

N
M
NAK NEK
R
S
x
T

23. Végezze el a feladatokat saját maga

m
T
Nak nek
m
D
Nak nek
T
Szerkesszünk metszetet: a) paralelepipedonból;
b) tetraéder
M, T, K pontokon áthaladó sík.

24. Felhasznált források

Soboleva L. I. Szakaszok építése
Tkacheva V.V. Szakaszok építése
tetraéder és paralelepipedon
Gobozova L.V. Építési problémák
szakaszok
DVD. Geometria leckék Kirill és
Methodius. 10. évfolyam, 2005
Képzési és tesztelési feladatok.
Geometria. 10. osztály (Notebook)/Aleshina
T.N. – M.: Értelemközpont, 1998

A planimetria axiómái:

A különböző tankönyvekben az egyenesek és a síkok tulajdonságait különböző módon lehet bemutatni, axióma, ebből származó következmény, tétel, lemma stb. Tekintsük Pogorelov A.V. tankönyvét.

Egy egyenes egy síkot két félsíkra oszt.

Bármely félegyenesből berajzolható egy adott félsíkú szög egy adott félsíkba. fokmérő, kevesebb, mint 180 0 , és csak egy.

Bármilyen háromszög is legyen, egy adott helyen van egy egyenlő háromszög egy adott félegyeneshez képest.

Egy adott egyenesen nem fekvő ponton keresztül a síkon legfeljebb egy, az adott egyenessel párhuzamos egyenest lehet húzni.

A sztereometria axiómái:

Bármi legyen is a sík, vannak pontok, amelyek ehhez a síkhoz tartoznak, és olyan pontok, amelyek nem tartoznak ehhez a síkhoz, és olyan pontok, amelyek nem tartoznak hozzá.

Ha két különböző síknak van közös pontja, akkor ezen a ponton átmenő egyenes mentén metszik egymást.

Ha két különböző egyenesnek van közös pontja, akkor sík húzható rajtuk keresztül, és csak egy.

Bármi legyen is az egyenes, vannak pontok, amelyek ehhez az egyeneshez tartoznak, és olyan pontok, amelyek nem tartoznak hozzá.

Bármely két ponton keresztül húzhat egy egyenest, és csak egyet.

Az egyenes három pontja közül csak egy van a másik kettő között.

Minden szegmensnek egy bizonyos hossza nagyobb, mint nulla. Egy szakasz hossza megegyezik azon részek hosszának összegével, amelyekre bármelyik pontja osztja.

Egy síkhoz tartozó egyenes ezt a síkot két félsíkra osztja.

Minden szögnek van egy bizonyos mértéke, amely nagyobb, mint nulla. Az egyenes szög 180 0 . Egy szög fokmértéke megegyezik azon szögek mértékének összegével, amelyekbe az oldalai között áthaladó bármely sugár felosztja.

A kezdőponttól számítva bármely félegyenesre megrajzolhat egy adott hosszúságú szakaszt, és csak egyet.

Az azt tartalmazó síkon egy félegyenesből 180-nál kisebb, adott fokszámú szög rajzolható egy adott félsíkra 0 , és csak egy.

Bármi is legyen a háromszög, egy adott síkban egy egyenlő háromszög van egy adott helyen az adott sík adott félegyeneséhez képest.

Egy síkon egy adott ponton keresztül, amely nem egy adott egyenesen fekszik, legfeljebb egy, az adottval párhuzamos egyenest lehet húzni.

Szakasz

A térben két alakzat, esetünkben egy sík és egy poliéder a következő kölcsönös elrendeződéssel rendelkezhet: nem metszi egymást, egy pontban metszi egymást, egyenes vonalban metszi és a sík a poliédert a belseje mentén metszi (1. ábra) , és ezzel egyidejűleg a következő ábrákat alkotják:

a) üres alak (nem metszik)

b) pont

c) szegmens

d) sokszög

Ha van egy sokszög egy poliéder és egy sík metszéspontjában, akkor ez a sokszögpoliéder síkszelvényének nevezzük .

1. ábra

Meghatározás. Szakasz térbeli test (például poliéder) a test és a sík metszéspontjából származó alak.

Vágó sík poliéder nevezzünk olyan síkot, amelynek mindkét oldalán egy adott poliéder pontjai vannak.

Csak azt az esetet vesszük figyelembe, amikor a sík a poliédert a belsejében metszi. Ebben az esetben ennek a síknak a metszéspontja a poliéder minden lapjával egy bizonyos szakasz lesz.

Ha a síkok egy egyenesben metszik egymást, akkor az egyenest nevezzükkövetve az egyik síkot a másikra.

Általában egy poliéder vágási síkja metszi minden lapjának síkját (valamint ennek a poliédernek bármely más vágási síkját). Szintén metszi azokat az egyeneseket, amelyeken a poliéder élei fekszenek.

Azt az egyenest, amely mentén a vágási sík metszi a poliéder bármely lapjának síkját, nevezzüka vágási síkot követve ennek a lapnak a síkján, és azt a pontot, ahol a vágási sík metszi a poliéder bármely élét tartalmazó egyenest, ún.a vágási síkot követve továbbezt az egyenest. Ez a pont egyben egy vonal nyoma is a vágási síkon. Ha a vágási sík közvetlenül metszi a poliéder lapját, akkor beszélhetünk a vágási sík nyomvonaláról a lapon, és hasonlóképpen kb.a vágási sík nyoma a poliéder szélén, vagyis egy él nyomáról egy vágási síkon.

Mivel az egyenest két pont egyedileg határozza meg, a vágási sík nyomának megtalálásához bármely más síkon és különösen a poliéder bármely lapjának síkján elegendő a síkok két közös pontját megszerkeszteni.

Egy vágási sík nyomvonalának, valamint egy poliéder metszetének ezzel a síkkal való megszerkesztéséhez nemcsak a poliédert, hanem a vágási síkot is meg kell adni. A metszősík felépítése pedig ennek a síknak a specifikációjától függ. A sík, és különösen a vágási sík meghatározásának fő módjai a következők:

három pont nem esik egy egyenesen;

egy egyenes és egy pont, amely nem fekszik rajta;

két párhuzamos egyenes;

két egymást metsző vonal;

egy pont és két metsző egyenes;

A vágási sík megadásának más módjai is lehetségesek.

Ezért a poliéderek metszeteinek felépítésére szolgáló összes módszer módszerekre osztható.

Módszerek poliéderek metszete készítésére

A poliéderek metszeteinek módszerét a sztereometriában építési problémákban alkalmazzák. Ez azon a képességen alapul, hogy meg lehet építeni egy poliéder szakaszát és meghatározni a szakasz típusát.

Három fő módszer létezik a poliéderek szakaszainak felépítésére:

Axiomatikus módszer:

Nyomkövetési módszer.

Kombinált módszer.

Koordináta módszer.

jegyzet hogy a nyomkövetési módszer és a segédmetszeti módszer fajtákAxiomatikus módszer metszetek felépítésére.

A poliéderek metszeteinek megalkotására a következő módszereket is megkülönböztethetjük:

poliéder metszetének szerkesztése egy adott ponton átmenő síkkal párhuzamos síkkal;

egy adott egyenesen átmenő szakasz építése egy másik adott egyenessel párhuzamosan;

egy adott ponton átmenő szakasz szerkesztése két adott metsző egyenessel párhuzamosan;

poliéder metszetének megalkotása egy adott síkra merőleges adott egyenesen átmenő síkkal;

poliéder metszetének szerkesztése egy adott ponton átmenő síkkal, amely egy adott egyenesre merőleges.

A metszetkészítés módszereit alkotó főbb műveletek az egyenes és a sík metszéspontjának megkeresése, két sík metszésvonalának megalkotása, a síkkal párhuzamos, a síkra merőleges egyenes megalkotása. Két sík metszésvonalának megszerkesztéséhez általában meg kell találni annak két pontját, és rajtuk keresztül kell húzni egy egyenest. Egy egyenes és egy sík metszéspontjának megszerkesztéséhez keressünk egy egyenest a síkban, amely metszi az adott metszéspontot. Ezután megkapjuk a kívánt pontot a talált egyenes és az adott metszéspontjában.

Nézzük külön az általunk felsoroltakatpoliéderek metszeteinek elkészítésének módszerei:

Nyomkövetési módszer.

Nyomkövetési módszer a sztereometria axiómáira épül (alapszik), a módszer lényege egy segédegyenes felépítése, amely a vágási sík és az ábra bármely lapjának síkjával való metszésvonal képe. A legkényelmesebb a vágási sík és az alsó alap sík metszésvonalának képét megszerkeszteni. Ezt a sorta vágási sík fő nyomának nevezik . Nyomvonal segítségével könnyen készíthetünk képeket a vágási sík pontjairól, amelyek az ábra oldalsó élein vagy lapjain helyezkednek el. Ezeknek a pontoknak a képeit következetesen összekapcsolva megkapjuk a kívánt szakasz képét.

Vegye figyelembe, hogy hogy egy vágósík főnyomának megalkotásakor a következő állítást használjuk.

Ha a pontok a vágási síkhoz tartoznak és nem ugyanazon az egyenesen fekszenek, és (középső vagy párhuzamos) vetületük a főként választott síkra, a pontok ill. akkor a megfelelő egyenesek metszéspontjai, vagyis a pontok és ugyanazon az egyenesen fekszenek (1. ábra, a, b).

1.a ábra 1.b ábra

Ez az egyenes vonal a vágási sík fő nyomvonala. Mivel a pontok a főnyomon helyezkednek el, ennek megszerkesztéséhez elegendő ebből a háromból két pontot találni.

A segédszelvények módszere.

Ez a poliéder szakaszok felépítésének módja meglehetősen univerzális. Azokban az esetekben, amikor a vágási sík kívánt nyoma (vagy nyomai) a rajzon kívül esik, ennek a módszernek még bizonyos előnyei is vannak. Ugyanakkor szem előtt kell tartani, hogy az ezzel a módszerrel végzett építkezések gyakran „zsúfoltnak” bizonyulnak. Néhány esetben azonban a segédszelvények módszere bizonyul a legracionálisabbnak.

Kombinált módszer

A poliéderek metszeteinek felépítésére szolgáló kombinált módszer lényege az egyenesek és síkok térbeli párhuzamosságára vonatkozó tételek alkalmazása az axiomatikus módszerrel kombinálva.

A szakaszok felépítésének koordinátamódszere.

A koordináta módszer lényege, hogy kiszámítjuk az élek vagy poliéder metszéspontjainak koordinátáit a vágási síkkal, amit a sík egyenlete ad meg. A vágási sík egyenletét a problémakörülmények alapján számítjuk ki.

jegyzet , hogy a poliéder metszetének ez a módszere elfogadható számítógép számára, mivel nagy mennyiségű számítással jár, ezért ezt a módszert célszerű számítógéppel megvalósítani.

Fő feladatunk az lesz, hogy egy poliéder metszetét egy síkkal, i.e. e két halmaz metszéspontjának megalkotásában.

Poliéder szakaszok építése

Mindenekelőtt megjegyezzük, hogy a konvex poliéder szakasza egy konvex lapos sokszög, amelynek csúcsai általános esetben a vágási sík metszéspontjai a poliéder éleivel, oldalai pedig a poliéder éleivel. arcok.

Példák a szakaszok felépítésére:

A szakasz meghatározásának módszerei nagyon változatosak. Ezek közül a legelterjedtebb az a módszer, amikor három olyan ponttal határozunk meg egy vágási síkot, amelyek nem ugyanazon az egyenesen helyezkednek el.

1. példa A paralelepipedon ABCDA-hoz 1 B 1 C 1 D 1 . Szerkesszünk M, N, L pontokon átmenő szakaszt.

Megoldás:

Kösd össze az AA síkban fekvő M és L pontot 1 D 1 D.

Metszük a szakaszhoz tartozó ML egyenest az A éllel 1 D 1 1 D 1 D. Szerezz X pontot 1 .

Az X1 pont az A élen található 1 D 1 , és ezért az A sík 1 B 1 C 1 D 1 , ugyanabban a síkban fekvő N öltéssel összekötjük.

x 1 N metszi az A élt 1 B 1 a K pontban.

Kösd össze a K és M pontokat, amelyek ugyanabban az AA síkban helyezkednek el 1 B 1 B.

Keressük meg a metszetsík és a DD sík metszésvonalát 1 C 1 C:

Metszük a szakaszhoz tartozó ML egyenest a DD éllel 1 , ugyanabban a síkban fekszenek AA 1 D 1 D, megkapjuk az X pontot 2 .

A szakaszhoz tartozó KN egyenest metsszük a D éllel 1 C 1 , ugyanabban az A síkban fekszenek 1 B 1 C 1 D 1 , megkapjuk az X3 pontot;

Az X2 és X3 pont a DD síkban található 1 C 1 C. Rajzolj egy X egyenest 2 x 3 , amely metszi a C élt 1 C a T pontban, és DC él a P pontban. Kössük össze az ABCD síkban fekvő L és P pontokat.

Így a probléma akkor tekinthető megoldottnak, ha megtaláltuk mindazokat a szegmenseket, amelyek mentén a sík metszi a poliéder lapjait, amit meg is tettünk. MKNTPL - a szükséges szakasz.

Jegyzet. Ugyanez a metszetkészítési probléma megoldható a párhuzamos síkok tulajdonságával.

A fentiek alapján létrehozhat egy algoritmust (szabályt) az ilyen típusú problémák megoldására.

A poliéderek metszeteinek felépítésének szabályai:

2. példa DL, M

Oldjuk meg axiomatikus módszerrel:

Rajzoljunk egy segédsíkotDKM, amely az AB és BC éleket az E és pontokban metsziF(a megoldás előrehaladása a 2. ábrán). Rajzoljuk meg a metszetsík CM-jének „nyomát” ezen a segédsíkon, keressük meg a CM és E metszéspontját.F– pont P. P pont, mintL, az ABC síkban fekszik, és lehet húzni egy egyenest, amely mentén a metszetsík metszi az ABC síkot (a metszet „nyoma” az ABC síkban).

3. példa A MABCD piramis AB és AD élein definiáljuk a P és Q pontokat, ezeknek az éleknek a felezőpontját, az MC élen pedig egy R pontot. Szerkesszük meg a piramisnak egy olyan szakaszát, amelyen egy sík megy át. P, Q és R pontok.

A megoldást kombinált módszerrel hajtjuk végre:

1). Nyilvánvaló, hogy a PQR sík fő nyomvonala a PQ egyenes.

2). Keressük meg azt a K pontot, ahol a MAC sík metszi a PQ egyenest. A K és R pontok a PQR és a MAC síkhoz egyaránt tartoznak. Ezért a KR egyenes megrajzolásával megkapjuk e síkok metszésvonalát.

3). Keressük meg az N=AC BD pontot, húzzunk egy MN egyenest és keressük meg az F=KR MN pontot.

4). Az F pont a PQR és MDB síkok közös pontja, vagyis ezek a síkok metszik egymást az F ponton áthaladó egyenes mentén. Mivel azonban PQ - középső vonal ABD háromszög, akkor PQ párhuzamos BD-vel, vagyis a PQ egyenes párhuzamos az MDB síkkal. Ekkor a PQ egyenesen átmenő PQR sík metszi az MDB síkot a PQ egyenessel párhuzamos egyenes mentén, azaz párhuzamos és egyenes BD-vel. Ezért az F ponton átmenő MDB síkban a BD egyenessel párhuzamos egyenest húzunk.

5). A további konstrukciók az ábrán láthatók. Ennek eredményeként megkapjuk a PQD"RB" sokszöget - a kívánt szakaszt

Tekintsük a prizma keresztmetszeteit az egyszerűség, vagyis a logikus gondolkodás megkönnyítése érdekében vegyük figyelembe a kocka szakaszait (3.a ábra):

Rizs. 3.a

A prizma oldaléleivel párhuzamos síkok metszete paralelogrammák. Különösen az átlós metszetek paralelogrammák (4. ábra).

Def. Átlós szakasz A prizmát egy olyan sík vágja, amely átmegy két olyan oldalélen, amelyek nem tartoznak ugyanahhoz a laphoz.

A prizma átlós metszetéből kapott sokszög egy paralelogramma. Kérdés az átlós szakaszok számáróln-szögprizma nehezebb, mint az átlók számának kérdése. Annyi szakasz lesz, ahány átló van az alapnál. Tudjuk, hogy a konvex prizmának konvex sokszögei vannak az alapjain, és egy konvex prizmánakn-gon az átlók. És így azt mondhatjuk, hogy feleannyi átlós szakasz van, mint átló.

Jegyzet: Az ábrán a paralelepipedon metszeteinek megalkotásánál figyelembe kell venni, hogy ha egy vágási sík egyes szakaszok mentén két szemközti oldalt metsz, akkor ezek a szakaszok párhuzamosak „a paralelepipedon tulajdonsága alapján, pl. A paralelepipedon szemközti oldalai párhuzamosak és egyenlőek.

Választ adunk a gyakran ismételt kérdésekre:

Milyen sokszögeket kapunk, ha egy kockát sík vág?

"háromszög, négyszög, ötszög, hatszög."

Vágható-e egy kockát sík hétszögre? Mi van a nyolcszöggel?

"nem tud".

3) Felmerül a kérdés: hány oldala van egy sokszögnek, ha egy poliédert síkkal vágunk?

A poliéder síkbeli vágásával kapott sokszög oldalainak legnagyobb száma megegyezik a poliéder lapjainak számával .

3. példa Szerkesszük meg az A prizma keresztmetszetét 1 B 1 C 1 D 1 ABCD három M, N, K ponton átmenő síkkal.

Tekintsük az M, N, K pontok elhelyezkedésének esetét a prizma felületén (5. ábra).

Fontolja meg az esetet: B ebben az esetben nyilván M1 = B1.

Építkezés:

4. példa Szerkessze meg a paralelepipedon ABCDA metszetét 1 B 1 C 1 D 1 az M, N, P pontokon áthaladó sík (a pontok a rajzon vannak feltüntetve (6. ábra)).

Megoldás:

Rizs. 6

Az N és P pontok a paralelepipedon metszetsíkjában és alsó bázisának síkjában helyezkednek el. Építsünk ezeken a pontokon átmenő egyenest. Ez az egyenes a vágási sík nyomvonala a paralelepipedon alapsíkjára.

Folytassuk azt az egyenest, amelyiken a paralelepipedon AB oldala fekszik. Az AB és NP egyenesek egy S pontban metszik egymást. Ez a pont a metszetsíkhoz tartozik.

Mivel az M pont is a metszetsíkhoz tartozik és metszi az AA egyenest 1 valamikor X.

Az X és N pont az AA lap azonos síkjában található 1 D 1 D, kösse össze őket, és kapjon XN egyenest.

Mivel a paralelepipedon lapjainak síkjai párhuzamosak, ezért az M ponton keresztül egyenest húzhatunk az A lapra 1 B 1 C 1 D 1 , párhuzamos az NP egyenessel. Ez a vonal metszi a B oldalt 1 VAL VEL 1 az Y pontban.

Hasonlóképpen húzunk YZ egyenest, párhuzamosan az XN egyenessel. Összekapcsoljuk a Z-t P-vel, és megkapjuk a kívánt szakaszt - MYZPNX.

A piramis csúcsán áthaladó síkok metszetei háromszögek. A háromszögek különösen átlós szakaszok. Ezek a gúla két nem szomszédos oldalsó élén átmenő síkok metszetei.

4. példa Szerkesszük meg az ABC piramis egy szakaszátDK pontokon áthaladó sík,L, M.

Megoldás:

Oldjuk meg ugyanezt a példát másképp .

Tegyük fel, hogy a K pontokbanL, és M épített szakaszKLNM(7. ábra). Jelöljük azzalFnégyszög átlóinak metszéspontjaKLNM. Csináljunk direktDFés jelöljeF 1 metszéspontja az ABC éllel. PontF 1 egybeesik az AM és SC egyenesek metszéspontjával (F 1 egyidejűleg az AM síkokhoz tartozikDÉsDSK). PontF 1 könnyen építhető. Ezután építünk egy pontotFmetszéspontkéntDF 1 ÉsL.M.. Ezután megtaláljuk a lényegetN.

A figyelembe vett technikát únbelső tervezési módszer . (A mi esetünkben arról beszélünk a központi tervezésről. NégyszögKAz MSA egy négyszög vetületeKMNLpontbólD. Ebben az esetben az átlók metszéspontjaKMNL- pontF– a négyszög átlóinak metszéspontjához megyKMSA - pontF 1 .

Egy poliéder metszeti területe.

A poliéder keresztmetszeti területének kiszámításának problémáját általában több szakaszban oldják meg. Ha a feladat azt állítja, hogy egy metszet készült (vagy vágási síkot rajzoltak stb.), akkor a megoldás első szakaszában meghatározzák a metszetben kapott ábra típusát.

Ezt meg kell tenni a megfelelő képlet kiválasztásához a keresztmetszeti terület kiszámításához. Miután tisztáztuk a szakaszban kapott ábra típusát, és kiválasztottuk a képletet az ábra területének kiszámításához, közvetlenül a számítási munkához folytatjuk.

Egyes esetekben könnyebb lehet, ha anélkül, hogy kitalálná a szakaszban kapott ábra típusát, a tételből következő képlet segítségével egyenesen a terület kiszámításához megy.

Tétel egy sokszög ortogonális vetületének területéről: Egy sokszög síkra merőleges vetületének területe egyenlő a területének és a sokszög síkja és a vetítési sík közötti szög koszinuszának szorzatával: .

A metszetterület kiszámításának helyes képlete: ahol a metszetben kapott ábra merőleges vetületének területe, és ez a vágási sík és az ábra vetítési síkja közötti szög. Ezzel a megoldással a metszetben kapott ábra merőleges vetületét kell megszerkeszteni és kiszámítani

Ha a problémafelvetés kimondja, hogy egy szakaszt meg kell építeni, és meg kell találni a kapott szakasz területét, akkor az első lépésben indokoltan meg kell alkotni az adott szakaszt, majd természetesen meg kell határozni a kapott ábra típusát. a szakasz stb.

Vegyük észre a következő tényt: mivel konvex poliéderek metszetei épülnek fel, ezért a metszetsokszög is konvex lesz, így a területe háromszögekre osztással megkereshető, azaz a metszet területe egyenlő a sokszög területeinek összegével. a háromszögek, amelyekből áll.

1. feladat.

– szabályos háromszög alakú gúla, amelynek alapoldala egyenlő, magassága pedig egyenlő. Szerkesszük meg a gúla egy szakaszát, amelynek síkja átmegy azokon a pontokon, ahol az oldal közepe van, és keressük meg a területét (8. ábra).

Megoldás.

A piramis keresztmetszete háromszög. Keressük meg a területét.

Mivel a piramis alapja egy egyenlő oldalú háromszög, a pont pedig az oldal felezőpontja, ez a magasság, majd .

A háromszög területe megtalálható:

2. feladat.

A szabályos prizma oldaléle megegyezik az alap oldalával. Szerkesszünk egy prizma szakaszait egy ponton átmenő síkkalA, merőleges az egyenesre Ha megtaláljuk a prizma kapott keresztmetszetének területét.

Megoldás.

Szerkesszük meg az adott szakaszt. Tegyük ezt tisztán geometriai megfontolások alapján, például a következőképpen.

Egy adott egyenesen és adott ponton átmenő síkban húzzunk egy egyenest, amely merőleges az ezen a ponton átmenő egyenesre (9. ábra). Erre a célra használjuk fel azt a tényt, hogy a háromszögben vagyis a mediánja ennek a háromszögnek a magassága is. Tehát egyenes.

A ponton keresztül húzunk egy másik egyenest az egyenesre merőlegesen. Rajzoljuk meg például egy egyenesen átmenő síkban. Nyilvánvaló, hogy ez a vonal az egyenes

Tehát két egymást metsző egyenest szerkesztünk, merőlegesen az egyenesre. Ezek az egyenesek egy, az egyenesre merőleges ponton átmenő síkot határoznak meg, vagyis egy vágósíkot adunk meg.

Szerkesszük meg a prizma egy szakaszát ezzel a síkkal. Vegye figyelembe, hogy mivel az egyenes párhuzamos a síkkal. Ekkor az egyenesen áthaladó sík a síkot az egyenessel párhuzamos egyenes mentén, azaz egy egyenes mentén metszi. Rajzoljunk egy egyenest a ponton keresztül, és kössük össze a kapott pontot egy ponttal.

Négyszög adott szakasz. Határozzuk meg a területét.