Pembinaan bahagian. Kerja penyelidikan mengenai topik "kaedah untuk membina bahagian polyhedra"

29.09.2019

Dalam tugasan sebelumnya, pengetahuan tentang teori adalah mencukupi untuk kami membina keratan rentas. Mari kita pertimbangkan masalah lain. Tugasan 1. Bina bahagian tetrahedron yang melalui titik M, selari dengan satah ABD. M Satu perkara tidak akan membantu kita dalam apa jua cara, tetapi masalahnya mempunyai syarat tambahan: bahagian itu mesti selari dengan satah ABD. Apa yang diberikan ini kepada kita? 1. Satah ADB dan DBC bersilang di sepanjang garis lurus DB, oleh itu bahagian yang selari dengan ADB memotong DBC sepanjang (Jika dua garis lurus selari selari dengan DB. satah bersilang dengan satu pertiga, maka garis persilangan adalah selari) M Titik M tergolong untuk menghadapi DBC. Mari kita lukis melaluinya N garis lurus MK selari dengan DB. 2. Begitu juga: (ADB) (ABC)=AB, K oleh itu keratan akan bersilang (ABC) dalam garis lurus selari dengan AB. K(ABC). Melalui titik K dalam satah ABC lukis garis lurus KN selari dengan AB. M N K N (ADC), M (ADC), oleh itu MN (ADC) (dan satah pemotongan). Mari kita menjalankan NM. MKN adalah bahagian yang diperlukan. Jadi: M N 1. Pembinaan: 1. Dalam satah (DBC) MK // DB, MK BC = K. 2. Dalam satah (ABC) KN // AB, KN AC = N. 3. MN Mari kita buktikan bahawa MKN ialah bahagian K 2 yang diperlukan. Bukti. 1. Bahagian itu melalui titik M 2. N (ADC), M (ADC) => NM (ADC) 3. MK // DB, NK // AB secara binaan, oleh itu (NMK) // (ABD) oleh atribut. Oleh itu, MKN ialah bahagian yang dikehendaki bagi b.t.c. Masalah 2. Bina satu bahagian ABCDA1B1C1D1 berpaip selari melalui bahagian tengah tepi D1C1 dan titik D, selari dengan garis lurus a. B1 C1 Penaakulan. M A1 D1 B A C D 1. Tandakan titik yang ditunjukkan dalam keadaan (mari sebut sewenang-wenangnya). M – tengah D1C1. 2. Titik M dan D terletak B1 C1 M A1 A, bermakna ia boleh disambungkan. D1 B C D dalam satah yang sama DD1C1, Tiada apa-apa lagi untuk disambungkan. 3. Mari kita gunakan syarat tambahan: satah pemotongan mestilah selari dengan garis lurus a. B1 C1 M A1 B C S A Untuk melakukan ini, ia mesti mengandungi garis selari dengan garis a. Cara paling mudah ialah melukis garis lurus sedemikian dalam satah ABC, kerana ia mengandungi garis lurus a dan titik D kepunyaan bahagian itu. D Dalam satah ABC, melalui titik D, lukis garis lurus DS selari dengan lurus a. DS AB = S. 4. Kerana (ABC) // (A1B1C1), lukis dalam satah (A1B1C1), melalui titik M, baris MP // SD. MP B1C1 = P 5. Kerana (DD1C1) // (AA1B1), kemudian dalam satah P B C (AA1B1) melalui titik S kita boleh melukis garis lurus M N A D SN selari dengan DM. SN BB1 = N 1 1 1 1 B C S A D 6. Titik N dan P terletak dalam satah (A1B1C1). Mari sambungkan mereka. SNPMD - bahagian yang diperlukan. Jadi: 1. Pembinaan. 1. MD B1 A1 N P C1 S A M 3. Dalam (A1B1C1), melalui titik M, MP // DS, MP B1C1 = P C 4. Dalam satah (AA1B1), melalui titik S, SN // DM, SN BB1 = N 5. NP D1 B D 2. Dalam (ABC), melalui titik D, DS // a, DS AB = S Mari kita buktikan bahawa SNPMD adalah bahagian yang diperlukan. 2. Bukti. B1 A1 N 1. Bahagian melalui titik D dan bahagian tengah tepi D1C1 - titik M melalui pembinaan. P C1 M C S A 3. PM // SD, P B1C1 oleh pembinaan D1 B D 2. DS // a, (S AB) oleh pembinaan, oleh itu (KNP) // a oleh atribut. 4. SN // DM, N BB1 secara pembinaan 5. P (BB1C1), N (BB1C1) => PN (BB1C1). Oleh itu, SNPMD ialah keratan rentas yang dikehendaki, dsb. Masalah 3. Bina bahagian paip selari selari dengan B1A dan melalui titik M dan N. Penaakulan. 1. Sambungkan M dan N (mereka terletak dalam satah (C1A1B1)). B1 N M A1 D1 B A C1 C D Tiada apa lagi yang boleh disambungkan. Mari kita gunakan syarat tambahan: satah pemotongan mestilah selari dengan garisan B1A 2. Agar satah pemotongan selari dengan AB1, ia perlu mengandungi garisan selari dengan AB1 (atau DC1, kerana DC // AB1 oleh sifat parallelepiped). Ia adalah paling mudah untuk menggambarkan garis lurus sedemikian di muka DD1C1C, kerana (DD1C1) // (AA1B1), dan AB1 (AA1B1). Mari kita lukis garis NK // AB1, NK DD1 = K dalam satah (DD1C1). B1 N M A1 D1 B 3. Sekarang dalam satah AA1D1 terdapat dua titik, M dan K, kepunyaan bahagian itu. Mari sambungkan mereka. C K A C1 D MNK – bahagian yang diperlukan. Jadi: 1. Pembinaan. 1. MN 2. Dalam satah (DD1C1) NK // AB1, NK DD1 = K. . B1 N A1 A M D1 C1 3. MK Mari kita buktikan bahawa MNK adalah bahagian yang diperlukan 2. Bukti. B C 1. Bahagian itu melalui titik M dan N. K 2. M (A1B1C1), N (A1B1C1) => D MN (A1B1C1). 3. M (ADD1), K (ADD1) => MK (ADD1). 4. Kerana NK // AB1 secara binaan, kemudian (MNK) // AB1 dengan keselarian garis dan satah. Oleh itu, MNK ialah bahagian yang dikehendaki bagi b.t.c. Tugasan 3. 1. Dalam DABC tetrahedron, bina bahagian dengan satah melalui tengah tepi DC, bucu B dan selari dengan garisan AC. 2. Bina keratan paip selari dengan satah melalui tengah tepi B1C1 dan titik K terletak pada tepi CD, selari dengan garis BD, jika DK: KC = 1: 3. M 3. Bina bahagian tetrahedron dengan satah yang melalui titik M dan C, selari lurus a (Rajah 1). Rajah 1 4. Dalam ABCDA1B1C1D1 berpaip selari, titik E tergolong dalam CD tepi. Bina bahagian selari dengan satah yang melalui titik ini dan selari dengan kapal terbang BC1D. 5. Bina bahagian selari dengan satah yang melalui AA1, selari dengan MN, di mana M ialah titik tengah AB, N ialah titik tengah BC. 6. Bina bahagian selari dengan satah melalui bahagian tengah tepi B1C1 selari dengan satah AA1C1.

KEMENTERIAN PENDIDIKAN, SAINSDAN BELIA REPUBLIK KRIMEA

AKADEMI SAINS KECIL "PENCARI"

Jabatan: matematik

Bahagian: matematik

KAEDAH UNTUK MEMBINA BAHAGIAN POLIHEDRON

Saya telah melakukan kerja:

_______________

pelajar kelas

Penasihat saintifik:

Abstrak

Kaedah untuk membina bahagian polyhedra

Jabatan: matematik

Bahagian: matematik

Penasihat saintifik:

Tujuan kajian adalah kajian pelbagai kaedah untuk membina bahagian polyhedra. Untuk ini danbahan teori mengenai topik ini telah dikaji, kaedah untuk menyelesaikan masalah membina bahagian adalah sistematik, contoh masalah mengenai penggunaan setiap kaedah diberikan, contoh masalah dalam peperiksaan negeri bersatu untuk membina bahagian dan mengira elemennya dipertimbangkan.

PENGENALAN…………………………………………………………………………………….3

SEKSYEN 1. PEMBINAAN BAHAGIAN POLIHEDRON BERDASARKAN SISTEM AKSIOM SEREOMETRI……………………………………………………4

BAHAGIAN 2. KAEDAH SARINGAN DALAM MEMBINA BAHAGIAN POLIHEDRON…………………………………………………………………………………………10

BAHAGIAN 3. KAEDAH REKA BENTUK DALAM

DALAM PEMBINAAN BAHAGIAN POLIHEDE………………………………14

BAHAGIAN 4. KAEDAH GABUNGAN UNTUK MEMBINA BAHAGIAN

POLYhedra………………………………………………………………17

BAHAGIAN 5. KAEDAH KOORDINASI UNTUK MEMBINA BAHAGIAN POLIHEDE…………………………………………………………………………………….19

KESIMPULAN………………………………………………………………25

RUJUKAN……………………………………………………26

PENGENALAN

Graduan perlu mengambil peperiksaan dalam bidang matematik, dan pengetahuan serta kebolehan untuk menyelesaikan masalah stereometrik adalah perlu mengikut urutan, untuk menulis peperiksaan inimata maksimum. Perkaitan Kerja ini melibatkan keperluan untuk bersedia secara bebas untuk peperiksaan, dan topik yang sedang dipertimbangkan adalah salah satu yang paling penting.

A analisis demo, diagnostik dan latihan Pilihan Peperiksaan Negeri Bersatu Dengan 2009-2014 menunjukkan bahawa 70% tugas geometri terdiri daripada tugas membina bahagian dan mengira elemennya- sudut, kawasan.

DALAM kurikulum tugas untuk membina bahagian polyhedra diberikan 2 waktu akademik, yang tidak mencukupi untuk mengkaji topik ini. Di sekolah, bahagian satah polyhedra dibina hanya berdasarkan aksiom dan teorem stereometri. Pada masa yang sama, terdapat kaedah lain untuk membina bahagian rata polyhedra. Yang paling berkesan ialah kaedah surih, kaedah reka bentuk dalaman dan kaedah gabungan. Sangat menarik dan menjanjikan dari segi aplikasi kepada penyelesaiannya pelbagai tugas kaedah koordinat. Jika polihedron diletakkan dalam sistem koordinat, dan satah pemotongan ditentukan oleh persamaan, maka pembinaan bahagian itu akan dikurangkan untuk mencari koordinat titik persilangan satah dengan tepi polihedron.

Objek kajian: kaedah untuk membina bahagian polyhedra.

Tujuan kajian: belajar pelbagai kaedah membina bahagian polyhedra.

Objektif kajian:

1) Kaji bahan teori mengenai topik ini.

2) Sistematisasi kaedah untuk menyelesaikan masalah membina bahagian.

3) Berikan contoh tugasan untuk menggunakan setiap kaedah.

4) Pertimbangkan contoh masalah dalam Peperiksaan Negeri Bersepadu tentang membina bahagian dan mengira elemennya.

SEKSYEN 1

PEMBINAAN BAHAGIAN POLIHEDRON

BERDASARKAN SISTEM AXIOM SEREOMETRI

Definisi. Bahagian polihedron oleh satah dipanggil angka geometri, iaitu set semua titik dalam ruang yang pada masa yang sama tergolong dalam polihedron dan satah tertentu; satah itu dipanggil satah pemotongan.

Permukaan polihedron terdiri daripada tepi - ruas dan muka - poligon rata. Oleh kerana garis lurus dan satah bersilang pada satu titik, dan dua satah bersilang sepanjang garis lurus, maka keratan polihedron oleh satah ialah poligon satah; bucu poligon ini ialah titik-titik persilangan satah pemotongan dengan tepi polihedron, dan sisi-sisinya ialah segmen di sepanjang satah pemotongan bersilang mukanya. Ini bermakna untuk membina bahagian yang dikehendaki bagi polihedron yang diberikan dengan satah α ia cukup untuk membina titik persilangannya dengan tepi polihedron. Kemudian sambungkan titik-titik ini secara berurutan dengan segmen.

Satah pemotongan α boleh ditentukan oleh: tiga titik yang tidak terletak pada garis lurus yang sama; garis lurus dan titik yang bukan miliknya; syarat lain yang menentukan kedudukannya secara relatif kepada polihedron tertentu. Sebagai contoh, dalam Rajah 1 satu bahagian piramid segi empat PABCD dibina oleh satah α, ditakrifkan oleh titik M, K dan H, masing-masing kepunyaan tepi PC, PD dan PB;

Rajah 1

Tugasan. Dalam ABC berpaip selari DA 1 B 1 C 1 D 1 membina bahagian dengan satah, melalui puncak C dan D 1 dan titik K bagi segmen B 1 C 1 (Rajah 2, a).

Penyelesaian. 1. T. Kepada . DENGAN ∈ DD 1 C 1, D 1 ∈ DD 1 C 1, kemudian mengikut aksiom (melalui dua titik, kepunyaan kapal terbang, melalui garis lurus, dan hanya satu) mari kita bina jejak CD 1 dalam satah DD 1 C 1 (Rajah 2, b).

2. Begitu juga dalam pesawat A 1 B 1 C 1 kita akan membina surih DK, dalam satah BB 1 C 1 kita akan membina surih CK.

3. D 1 KC – bahagian yang dikehendaki (Gamb..2, c)

a B C)

Rajah.2

Tugasan. Bina satu bahagian piramid RABC dengan satah α = (MKH), di mana M, K dan H ialah titik dalaman bagi tepi RS, PB dan AB, masing-masing (Rajah 3, a).

Penyelesaian. langkah pertama. Titik M dan K terletak pada setiap dua satah α dan RVS. Oleh itu, mengikut aksiom persilangan dua satah, satah α bersilang dengan satah RVS di sepanjang garis lurus MK. Akibatnya, segmen MK ialah salah satu sisi bahagian yang dikehendaki (Rajah 3, b).

langkah ke-2. Begitu juga, segmen KN ialah bahagian lain bahagian yang dikehendaki (Rajah 3, c).

langkah ke-3. Titik M dan H tidak terletak serentak pada mana-mana muka piramid RABC, oleh itu segmen MH bukan sebelah bahagian piramid ini. Garis lurus KN dan RA terletak pada satah muka AVR dan bersilang. Mari kita bina titik T= KH ∩AP (Rajah 3, d).

Oleh kerana garis lurus KN terletak pada satah α, maka titik T terletak pada satah α. Sekarang kita lihat bahawa pesawat α dan APC mempunyai titik sepunya M dan T. Akibatnya, menurut aksiom persilangan dua satah, satah α dan satah APC bersilang di sepanjang garis lurus MT, yang, seterusnya, bersilang tepi AC pada titik R (Rajah 3, e) .

langkah ke-4. Sekarang, dengan cara yang sama seperti dalam langkah 1, kami menetapkan bahawa satah α bersilang muka ACP dan ABC di sepanjang segmen MR dan HR, masing-masing. Akibatnya, bahagian yang diperlukan ialah segi empat MKHR (Rajah 3, f).

Rajah.3

Mari kita pertimbangkan masalah yang lebih kompleks.

Tugasan . Bina satu bahagian piramid pentagonal PABCDE dengan satah

α = (KQR), di mana K, Q ialah titik dalaman bagi tepi RA dan RS, masing-masing, dan titik R terletak di dalam muka DPE (Rajah 4, a).

Penyelesaian . Garis QK dan AC terletak pada satah ACP yang sama (mengikut aksiom garis lurus dan satah) dan bersilang pada satu titik T 1 , (Rajah 4,b), manakala T 1 є α, sejak QК є α.

Garis lurus PR bersilang DE pada satu titik F (Rajah 4, c), iaitu titik persilangan satah ARR dan sisi DE tapak piramid. Kemudian garisan KR dan AF terletak pada satah ARR yang sama dan bersilang pada satu titik T 2 (Rajah 4, d), manakala T 2 є α , sebagai titik garis lurus KR є α (mengikut aksiom garis lurus dan satah).

Diterima: straight T 1 T 2 terletak pada satah pemotongan α dan pada satah asas piramid (mengikut aksiom garis lurus dan satah), manakala garis lurus bersilang dengan sisi DE dan AE tapak ABCDE piramid, masing-masing, pada titik M dan N (Rajah 4, e), yang merupakan titik persilangan satah α dengan tepi DE dan AE piramid dan berfungsi sebagai bucu bahagian yang dikehendaki.

Selanjutnya, garis lurus MR terletak pada satah muka DPE dan dalam satah pemotongan α (mengikut aksiom garis lurus dan satah), sambil bersilang tepi PD pada satu titik H - satu lagi puncak bahagian yang dikehendaki. (Rajah 4, f).

Seterusnya, mari kita bina titik T 3 - T 1 T 2 ∩ AB (Rajah 4, g), yang, sebagai titik garis lurus T 1 T 2 є α, terletak pada satah a (mengikut aksiom garis dan satah). Kini satah muka RAB tergolong dalam dua mata T 3 dan Kepada satah pemotongan α, yang bermaksud garis lurus T 3 K ialah garis lurus persilangan satah ini. Lurus T 3 K bersilang tepi PB pada titik L (Rajah 4, h), yang berfungsi sebagai bucu seterusnya bagi bahagian yang dikehendaki.

Oleh itu, "rantai" urutan untuk membina bahagian yang dikehendaki adalah seperti berikut:

1. T 1 = QK∩ AC ; 2. F = PR ∩ DE;

3. T 2 = KR ∩ AF; 4. M = T 1 T 2 ∩ DE;

5.N= T 1 T 2 ∩ AE ; 6. N = MR ∩ PD;

7. T 3 = T 1 T 2 ∩ AB ; 8.L=T 3 K ∩ PB.

Heksagon MNKLQH ialah bahagian yang diperlukan.

Rajah.4

Satu bahagian polihedron dengan muka selari (prisma, kubus selari) boleh dibina menggunakan sifat satah selari.

Tugasan . Titik M, P dan R terletak di tepi saluran selari. Dengan menggunakan sifat garis dan satah selari, bina satu keratan paip selari ini oleh satah MPR.

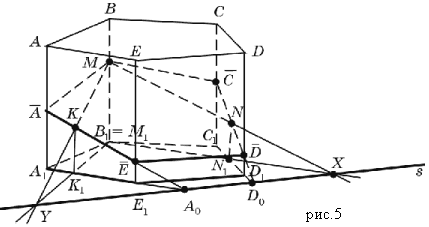
Penyelesaian. Biarkan titik M, P dan R terletak di tepi DD, masing-masing 1, BB 1 dan SS 1 selari ABCBA 1 B 1 C 1 B 1 (Rajah 5, a).

Mari kita nyatakan: (MPR) = α - satah pemotongan. Kami melukis segmen MR dan PR (Rajah 5, b), di mana satah α bersilang dengan muka CC, masing-masing 1 D 1 D dan BB 1 C 1 Daripada parallelepiped ini. Segmen MR dan PR adalah sisi bahagian yang dikehendaki. Seterusnya kita menggunakan teorem pada persilangan dua satah selari dengan satu pertiga.

Oleh kerana muka AA ialah 1 B 1 B adalah selari dengan menghadap CC 1 D 1 D, kemudian garis lurus persilangan satah α dengan satah muka AA 1 dalam 1 B mestilah selari dengan garisan MR. Oleh itu kita lukis segmen PQ || MR, Q є AB (Rajah 5, c); segmen PQ ialah sebelah sebelah bahagian yang dikehendaki. Begitu juga sejak menghadapi AA 1 D 1 D adalah selari dengan menghadap CC 1 dalam 1 B, kemudian garis lurus persilangan satah α dengan satah muka AA 1 D 1 D mesti selari dengan garis PR. Oleh itu, kami melukis segmen MH || PR, H = AD (Rajah 5, c); segmen MH ialah bahagian lain dari bahagian yang dikehendaki. Pada tepi AB dan AD muka ABCD, titik Q є AB dan H є AD telah dibina, yang merupakan bucu bahagian yang dikehendaki. Kami melukis segmen QH dan mendapatkan pentagon MRPQH - bahagian parallelepiped yang dikehendaki.

a B C)

nasi. 5

BAHAGIAN 2

KAEDAH SURUHAN DALAM MEMBINA BAHAGIAN POLIHEDRON

Definisi. Garis lurus sepanjang satah pemotongan α bersilang dengan satah tapak polihedron dipanggil jejak satah α dalam satah tapak ini.

Daripada takrifan surih yang kita perolehi: pada setiap titiknya garis lurus bersilang, satu daripadanya terletak pada satah sekan, satu lagi pada satah tapak. Sifat surih inilah yang digunakan semasa membina bahagian satah polyhedra menggunakan kaedah surih. Dalam kes ini, dalam satah pemotongan adalah mudah untuk menggunakan garis lurus yang bersilang dengan tepi polihedron.

Mula-mula, kita mentakrifkan satah sekan dengan jejaknya dalam satah tapak prisma (piramid) dan dengan titik kepunyaan permukaan prisma (piramid).

Tugasan. Bina keratan rentas prisma ABCVEA 1 B 1 C 1 D 1 E 1 satah α, yang diberikan oleh yang berikutl dalam satah ABC tapak prisma dan titik M kepunyaan tepi DD 1 (Gamb. 7, a).

Penyelesaian. Analisis. Mari kita andaikan bahawa pentagon MNPQR ialah bahagian yang dikehendaki (Rajah 6). Untuk membina pentagon rata ini, cukup untuk membina bucunya N, P, Q, R (titik M diberikan) - titik persilangan satah pemotong α dengan tepi, masing-masing CC 1, BB 1, AA 1, EE 1 prisma ini.

nasi. 6

Untuk membina titik N = α ∩ СС 1 ia cukup untuk membina garis lurus persilangan satah pemotong α dengan satah muka СDD 1 C 1 . Untuk melakukan ini, pada gilirannya, sudah cukup untuk membina satu lagi titik dalam satah muka ini, kepunyaan satah pemotongan α. Bagaimana untuk membina titik sedemikian?

Memandangkan ia lurus l terletak pada satah tapak prisma, maka ia boleh bersilang dengan satah muka CDD 1 C 1 hanya pada titik yang tergolong dalam baris CD = (CDD 1 ) ∩ (ABC), iaitu. titik X =l∩CD = l∩ (CDD 1 ) tergolong dalam satah pemotongan α. Oleh itu, untuk membina titik N = α ∩ СС 1 ia cukup untuk membina titik X =l ∩CD. Begitu juga, untuk membina titik P = α ∩ BB 1, Q = α ∩ AA 1 dan R = α ∩ EE 1 ia cukup untuk membina mata dengan sewajarnya: Y =l∩ BC, Z = l∩ AB dan T = l∩ AE. Dari sini

Pembinaan.

X = l∩ CD (Rajah 7, b);

N = MX ∩ СС 1 (Rajah 7, b);

Y = l∩ BC (Rajah 7, c);

P = NY ∩ BB 1 (Rajah 7, c);

Z= l∩ AB (Rajah 7, c);

Q= PZ ∩ AA 1 (Rajah 7, d);

T= l∩ AE (Rajah 6);

R= QT ∩ EE 1 (Rajah 6).

Pentagon MNPQR ialah bahagian yang diperlukan (Rajah 6).

Bukti . Memandangkan ia lurus l ialah jejak satah pemotongan α, maka titik X =l∩ СD, Y = l∩ BC, Z = l∩ AB dan T= l ∩ AE tergolong dalam pesawat ini.

Oleh itu kami mempunyai:

М є α , X є α => МХ є α, kemudian МХ ∩ СС 1 = N є α, yang bermaksud N = α ∩ СС 1 ;

N є α, Y є α => NY є α, kemudian NY ∩ ВВ 1 = Р є α, yang bermaksud Р = α ∩ ВВ 1 ;

Р є α, Z є α => РZ є α, kemudian PZ ∩ AA 1 = Q є α, yang bermaksud Q = α ∩ AA 1 ;

Q є α, T є α => QТ є α, kemudian QТ ∩ EE 1 =R є α, yang bermaksud R = α ∩ Е 1 .

Oleh itu, MNPQR adalah bahagian yang diperlukan.

a) b)

c) d)

nasi. 7

Belajar. Jejak l satah pemotong α tidak bersilang dengan tapak prisma, dan titik M satah pemotong tergolong dalam tepi sisi DD 1 prisma. Oleh itu, satah pemotongan α tidak selari dengan tepi sisi. Akibatnya, titik N, P, Q dan R persilangan satah ini dengan tepi sisi prisma (atau lanjutan tepi ini) sentiasa wujud. Dan kerana, sebagai tambahan, titik M tidak tergolong dalam jejakl , maka satah α yang ditakrifkan oleh mereka adalah unik. Ini bermakna bahawa masalah itu mempunyai penyelesaian yang unik.

Tugasan. Bina satu bahagian piramid pentagonal PABCDE dengan satah yang diberikan oleh yang berikutl dan titik dalaman K tepi PE.

Penyelesaian. Secara skematik, pembinaan bahagian yang dikehendaki boleh digambarkan seperti berikut (Rajah 8): T 1 → Q → T 2 → R → T 3 → M → T 4 → N.

Pentagon MNKQR ialah bahagian yang diperlukan.

"Rantai" urutan membina bucu bahagian adalah seperti berikut:

1. T 1 = l∩ AE; 2. Q = T 1 K ∩ RA;

3. T 2 = l∩ AB; 4. R = T 2 Q ∩ РВ;

5. T 3 = l∩ SM; 6. M = T 3 R ∩ RS;

7. T 4 = l∩CD; 8. N = T 4 M ∩ РD.

nasi. 8

Satah pemotongan sering ditakrifkan oleh tiga mata kepunyaan polihedron. Dalam kes ini, untuk membina bahagian yang dikehendaki menggunakan kaedah surih, mula-mula bina surih satah pemotongan dalam satah asas polihedron yang diberikan.

BAHAGIAN 3

KAEDAH REKA BENTUK DALAMAN

DALAM PEMBINAAN BAHAGIAN POLIHEDRON

Kaedah reka bentuk dalaman juga dipanggil kaedah surat-menyurat, atau kaedah bahagian pepenjuru.

Apabila menggunakan kaedah ini, setiap titik yang diberikan diunjurkan ke satah asas. Terdapat dua jenis yang mungkin reka bentuk: tengah dan selari. Unjuran pusat biasanya digunakan apabila membina bahagian piramid, dengan bahagian atas piramid menjadi pusat unjuran. Reka bentuk selari digunakan semasa membina keratan prisma.

Tugasan . Bina bahagian piramid PABCDE dengan satah α = (MFR), jika titik M, F dan R masing-masing ialah titik dalaman tepi RA, RS dan PE (Rajah 9, a).

Penyelesaian . Mari kita nyatakan satah tapak piramid itu sebagai β. Untuk membina bahagian yang dikehendaki, kami membina titik persilangan satah pemotong α dengan tepi piramid.

Mari kita bina titik persilangan satah pemotongan dengan tepi PD piramid ini.

Satah APD dan CPE bersilang satah β sepanjang garis lurus AD dan CE, masing-masing, yang bersilang pada satu titik K (Rajah 9, c). Garis lurus PK=(APD) ∩(CPE) memotong garis lurus FR є α pada satu titik K 1 HINGGA 1 = RK ∩ FR (Rajah 9, d), manakala K 1 є α. Kemudian: M є α, K 1 є α => garis lurus MK є a. Oleh itu titik Q = MK 1 ∩ PD (Rajah 9, e) ialah titik persilangan tepi PD dan satah pemotongan: Q = α ∩ PD. Titik Q ialah puncak bahagian yang dikehendaki. Begitu juga, kami membina titik persilangan satah α dan tepi PB. Satah BPE dan АD bersilang satah β sepanjang garis lurus BE dan AD, masing-masing, yang bersilang pada titik H (Rajah 9, e). Garis lurus PH = (BPE) ∩ (APD) bersilang garis lurus MQ pada titik H 1 (Gamb. 9, g). Kemudian garis lurus RN 1 bersilang tepi PB pada titik N = α ∩ PB - puncak bahagian (Rajah 9, h).

1. K = AD ∩ EC; 2. K 1 = RK ∩ RF;

3.Q= MK 1 ∩ R D; 4. H = BE ∩ A D;

5. Н 1 = РН ∩ МQ; 6. N = RН 1 ∩ РВ.

Pentagon MNFQR ialah bahagian yang diperlukan (Rajah 9, i).

a B C)

di mana)

g) h) i)

nasi. 9

Tugasan . Bina keratan rentas prisma ABCDEA 1 B 1 C 1 D 1 E 1 , satah α, ditakrifkan oleh titik M є BB 1, P DD 1, Q EE 1 (Gamb. 10).

Penyelesaian. Mari kita nyatakan: β - satah tapak bawah prisma itu. Untuk membina bahagian yang dikehendaki, kami membina titik persilangan satah α = (MPQ) dengan tepi prisma.

Mari kita bina titik persilangan satah α dengan tepi AA 1 .

Pesawat A 1 AD dan BEE 1 memotong satah β di sepanjang garis lurus AD dan BE, masing-masing, yang bersilang pada satu titik K. Oleh kerana satah A 1 AD dan BEE 1 melalui tepi selari AA 1 dan BB 1 prisma dan mempunyai titik sepunya K, kemudian garis lurus KK 1 persilangan mereka melalui titik K dan selari dengan tepi BB 1 . Mari kita nyatakan titik persilangan garis ini dengan garis QM: K 1 = KK 1 ∩ QM, KK 1 ║ BB 1 . Oleh kerana QM є α, maka K 1 є α.

nasi. 10

Diterima: Р є α, K 1 є α => lurus RK 1 є α, manakala RK 1 ∩ AA 1 = R. Titik R berfungsi sebagai titik persilangan satah α dan tepi AA 1 (R = α ∩ AA 1 ), oleh itu ialah puncak bahagian yang dikehendaki. Begitu juga, kita membina titik N = α ∩ СС 1 .

Oleh itu, urutan "langkah" untuk membina bahagian yang dikehendaki adalah seperti berikut:

K = AD ∩ BE; 2. K 1 = KK 1 ∩ MQ, KK 1 || BB 1;

R = RK 1 ∩ AA 1 ; 4. H = EC ∩AD;

H 1 – HH 1 ∩ РR, НН 1 || CC 1; 6.N = QН 1 ∩ СС 1.

Pentagon MNPQR ialah bahagian yang diperlukan.

Dalam pelajaran ini kita akan melihat tetrahedron dan unsur-unsurnya (tepi tetrahedron, permukaan, muka, bucu). Dan kami akan menyelesaikan beberapa masalah untuk membina bahagian dalam tetrahedron menggunakan kaedah umum untuk membina bahagian.

Topik: Keselarian garis dan satah

Pelajaran: Tetrahedron. Masalah membina bahagian dalam tetrahedron

Bagaimana untuk membina tetrahedron? Mari kita ambil segi tiga sewenang-wenangnya ABC. Apa-apa perkara D, tidak terletak pada satah segi tiga ini. Kami mendapat 4 segi tiga. Permukaan yang dibentuk oleh 4 segi tiga ini dipanggil tetrahedron (Rajah 1.). Titik dalaman yang dibatasi oleh permukaan ini juga merupakan sebahagian daripada tetrahedron.

nasi. 1. Tetrahedron ABCD

Unsur-unsur tetrahedron
A,B, C, D - bucu tetrahedron.
AB, A.C., AD, B.C., BD, CD - tepi tetrahedron.
ABC, ABD, BDC, ADC - muka tetrahedron.

Ulasan: boleh diambil rata ABC belakang asas tetrahedron, dan kemudian tunjuk D ialah puncak tetrahedron. Setiap tepi tetrahedron ialah persilangan dua satah. Contohnya, tulang rusuk AB- ini adalah persimpangan pesawat ABD Dan ABC. Setiap bucu tetrahedron ialah persilangan tiga satah. Puncak A terletak di dalam pesawat ABC, ABD, ADDENGAN. titik A ialah persilangan tiga satah yang ditetapkan. Fakta ini ditulis seperti berikut: A= ABC ∩ ABD ∩ ACD.

Definisi Tetrahedron

Jadi, tetrahedron ialah permukaan yang dibentuk oleh empat segi tiga.

Tepi Tetrahedron- garis persilangan dua satah tetrahedron.

Buat 4 segi tiga sama daripada 6 padanan. Tidak mustahil untuk menyelesaikan masalah di atas kapal terbang. Dan ini mudah dilakukan di angkasa. Mari kita ambil tetrahedron. 6 padanan ialah tepinya, empat muka tetrahedron dan akan menjadi empat segi tiga sama. Masalah selesai.

Diberi tetrahedron ABCD. titik M tergolong dalam pinggir tetrahedron AB, titik N tergolong dalam pinggir tetrahedron DALAMD dan tempoh R kepunyaan tepi DDENGAN(Gamb. 2.). Bina bahagian tetrahedron dengan satah MNP.

nasi. 2. Lukisan untuk masalah 2 - Bina bahagian tetrahedron dengan satah

Penyelesaian:
Pertimbangkan wajah tetrahedron Dmatahari. Pada muka ini N Dan P kepunyaan muka Dmatahari, dan oleh itu tetrahedron. Tetapi mengikut keadaan titik N, P tergolong dalam satah pemotongan. Bermaksud, NP- ini ialah garis persilangan dua satah: satah muka Dmatahari dan memotong satah. Mari kita anggap bahawa garis lurus NP Dan matahari tidak selari. Mereka berbaring dalam pesawat yang sama DMatahari. Mari kita cari titik persilangan garis NP Dan matahari. Mari kita nyatakan E(Gamb. 3.).

nasi. 3. Melukis untuk masalah 2. Mencari titik E

titik E tergolong dalam satah keratan MNP, kerana ia terletak pada talian NP, dan garis lurus NP terletak sepenuhnya pada satah keratan MNP.

Juga tunjuk E terletak di dalam kapal terbang ABC, kerana ia terletak pada garis lurus matahari keluar dari kapal terbang ABC.

Kami dapat itu MAKAN- garis persilangan pesawat ABC Dan MNP, sejak mata E Dan M berbaring serentak dalam dua satah - ABC Dan MNP. Mari kita sambungkan titik M Dan E, dan teruskan lurus MAKAN ke persimpangan dengan garisan AC. Titik persilangan garis MAKAN Dan AC mari kita nyatakan Q.

Jadi dalam kes ini NPQМ- bahagian yang diperlukan.

nasi. 4. Lukisan untuk masalah 2. Penyelesaian masalah 2

Sekarang mari kita pertimbangkan kes bila NP selari B.C.. Jika lurus NP selari dengan beberapa garis, contohnya, garis lurus matahari keluar dari kapal terbang ABC, kemudian lurus NP selari dengan keseluruhan satah ABC.

Satah bahagian yang dikehendaki melalui garis lurus NP, selari dengan kapal terbang ABC, dan memotong satah dalam garis lurus MQ. Jadi garis persimpangan MQ selari dengan garisan NP. Kita mendapatkan NPQМ- bahagian yang diperlukan.

titik M terletak di sebelah ADDALAM tetrahedron ABCD. Bina bahagian tetrahedron dengan satah yang melalui titik itu M selari dengan tapak ABC.

nasi. 5. Lukisan untuk masalah 3 Bina bahagian tetrahedron dengan satah

Penyelesaian:
Memotong kapal terbang φ selari dengan kapal terbang ABC mengikut syarat, ini bermakna bahawa pesawat ini φ selari dengan garisan AB, AC, matahari.
Dalam kapal terbang ABD melalui titik M jom buat direct PQ selari AB(Gamb. 5). Lurus PQ terletak di dalam kapal terbang ABD. Begitu juga dalam kapal terbang ACD melalui titik R jom buat direct PR selari AC. Dapat point R. Dua garis bersilang PQ Dan PR kapal terbang PQR masing-masing selari dengan dua garis bersilang AB Dan AC kapal terbang ABC, yang bermaksud kapal terbang ABC Dan PQR selari. PQR- bahagian yang diperlukan. Masalah selesai.

Diberi tetrahedron ABCD. titik M- titik dalaman, titik pada muka tetrahedron ABD. N- titik dalaman segmen DDENGAN(Gamb. 6.). Bina titik persilangan garis N.M. dan kapal terbang ABC.

nasi. 6. Lukisan untuk masalah 4

Penyelesaian:
Untuk menyelesaikannya, kami akan membina satah tambahan DMN. Biar lurus DM memotong garis AB pada titik KEPADA(Gamb. 7.). Kemudian, SKD- ini adalah bahagian pesawat DMN dan tetrahedron. Dalam kapal terbang DMN dusta dan lurus N.M., dan garis lurus yang terhasil SK. Jadi kalau N.M. tidak selari SK, maka mereka akan bersilang pada satu ketika R. titik R dan akan terdapat titik persilangan yang dikehendaki bagi garisan itu N.M. dan kapal terbang ABC.

nasi. 7. Lukisan untuk masalah 4. Penyelesaian masalah 4

Diberi tetrahedron ABCD. M- titik dalaman muka ABD. R- titik dalaman muka ABC. N- titik dalaman tepi DDENGAN(Gamb. 8.). Bina bahagian tetrahedron dengan satah yang melalui titik-titik itu M, N Dan R.

nasi. 8. Lukisan untuk masalah 5 Bina bahagian tetrahedron dengan satah

Penyelesaian:
Mari kita pertimbangkan kes pertama, apabila garis lurus MN tidak selari dengan kapal terbang ABC. Dalam masalah sebelum ini kami mendapati titik persilangan garis MN dan kapal terbang ABC. Inilah intinya KEPADA, ia diperoleh menggunakan satah tambahan DMN, iaitu kami buat DM dan kami mendapat satu mata F. Kami laksanakan CF dan di persimpangan MN kita dapat satu mata KEPADA.

nasi. 9. Melukis untuk masalah 5. Mencari titik K

Jom buat direct KR. Lurus KR terletak pada kedua-dua satah keratan dan dalam satah ABC. Mendapat mata P 1 Dan R 2. Menyambung P 1 Dan M dan sebagai kesinambungan kami mendapat maksudnya M 1. Menyambung titik R 2 Dan N. Hasilnya, kami memperoleh bahagian yang dikehendaki Р 1 Р 2 NM 1. Masalah dalam kes pertama diselesaikan.
Mari kita pertimbangkan kes kedua, apabila garis lurus MN selari dengan kapal terbang ABC. kapal terbang MNP melalui garis lurus MN selari dengan kapal terbang ABC dan bersilang dengan pesawat ABC sepanjang beberapa garis lurus R 1 R 2, kemudian lurus R 1 R 2 selari dengan garisan yang diberi MN(Gamb. 10.).

nasi. 10. Lukisan untuk masalah 5. Bahagian yang diperlukan

Sekarang mari kita lukis garis lurus R 1 M dan kami mendapat satu mata M 1.Р 1 Р 2 NM 1- bahagian yang diperlukan.

Jadi, kami melihat tetrahedron, menyelesaikan beberapa tugas biasa kepada tetrahedron. Dalam pelajaran seterusnya kita akan melihat parallelepiped.

1. I. M. Smirnova, V. A. Smirnov. - Edisi ke-5, diperbetulkan dan dikembangkan - M.: Mnemosyne, 2008. - 288 p. : sakit. Geometri. Darjah 10-11: buku teks untuk pelajar institusi pendidikan(peringkat asas dan profil)

2. Sharygin I.F. - M.: Bustard, 1999. - 208 p.: sakit. Geometri. Darjah 10-11: Buku teks untuk institusi pendidikan am

3. E. V. Potoskuev, L. I. Zvalich. - Edisi ke-6, stereotaip. - M.: Bustard, 008. - 233 p. :il. Geometri. Gred 10: Buku teks untuk institusi pendidikan am dengan kajian matematik yang mendalam dan khusus

Sumber web tambahan

2. Cara membina keratan rentas tetrahedron. Matematik ().

3. Perayaan idea pedagogi ().

Lakukan masalah di rumah mengenai topik "Tetrahedron", bagaimana untuk mencari tepi tetrahedron, muka tetrahedron, bucu dan permukaan tetrahedron

1. Geometri. Gred 10-11: buku teks untuk pelajar institusi pendidikan am (peringkat asas dan khusus) I. M. Smirnova, V. A. Smirnov. - Edisi ke-5, diperbetulkan dan dikembangkan - M.: Mnemosyne, 2008. - 288 ms: ill. Tugasan 18, 19, 20 ms 50

2. Titik E tengah rusuk MA tetrahedron MAVS. Bina bahagian tetrahedron dengan satah yang melalui titik-titik itu B, C Dan E.

3. Dalam tetrahedron MABC, titik M kepunyaan muka AMV, titik P kepunyaan muka BMC, titik K kepunyaan AC tepi. Bina bahagian tetrahedron dengan satah yang melalui titik-titik itu M, R, K.

4. Apakah bentuk yang boleh diperoleh hasil daripada persilangan tetrahedron dengan satah?

Matlamat kerja:
Pembangunan konsep spatial.
Tugasan:
1. Memperkenalkan peraturan untuk membina bahagian.
2. Membangunkan kemahiran dalam membina bahagian
tetrahedron dan parallelepiped pada berbeza
kes menentukan satah pemotongan.
3. Membangunkan keupayaan untuk menggunakan peraturan
membina bahagian semasa menyelesaikan masalah pada
topik "Polyhedra".

Untuk menyelesaikan banyak
geometri
tugasan yang diperlukan
membina bahagian
polyhedra
pelbagai
kapal terbang.

Konsep satah pemotongan

Sekan
kapal terbang
parallelepiped
(tetrahedron)
dipanggil mana-mana
kapal terbang, di kedua-dua belah pihak
sisi dari
yang mempunyai
mata yang diberikan
parallelepiped
(tetrahedron).

Konsep keratan polihedron

Memotong kapal terbang
melintasi tepi
tetrahedron
(parallelepiped) oleh
segmen.
Poligon, sisi
data yang manakah
segmen dipanggil
keratan rentas tetrahedron
(parallelepiped).

Bekerja daripada lukisan

Berapakah bilangan satah yang boleh dilukis
melalui elemen terpilih?
Apakah aksiom dan teorem yang anda gunakan?

Untuk membina bahagian
perlu merancang mata
persimpangan secant
satah dengan tepi dan
menghubungkan mereka dengan segmen.

Peraturan untuk membina bahagian

1. Anda hanya boleh menyambung dua
mata terletak pada satah satu
tepi.
2. Satah pemotong bersilang
muka selari sepanjang
segmen selari.

Peraturan untuk membina bahagian

3. Jika satah muka ditanda
hanya satu mata milik
satah keratan, maka ia adalah perlu
membina titik tambahan.
Untuk melakukan ini, anda perlu mencari mata
persimpangan yang telah dibina
garis lurus dengan garis lurus yang lain,
berbaring di tepi yang sama.

10. Pembinaan bahagian tetrahedron

11.

Tetrahedron mempunyai 4 muka
Dalam bahagian ia mungkin berubah
Segi tiga
segi empat

12.

Bina keratan rentas tetrahedron
Pesawat DABC melintas
melalui titik M,N,K
1. Mari kita lukis garis lurus melalui
mata M dan K, kerana mereka berbohong
dalam satu muka (ADC).
D
M
A.A.
N
K
BB
CC
2. Mari kita lukis garis lurus melalui
titik K dan N, kerana mereka
berbaring di sisi yang sama
(CDB).
3. Berhujah sama,
lukis garis lurus MN.
4. Segitiga MNK –
bahagian yang dikehendaki.

13. melalui titik M selari dengan ABC.

D
1. Mari kita lukis melalui titik M
selari lurus
tepi AB
2.
M
R
A
KEPADA
DENGAN
DALAM
Mari kita melalui titik M
selari lurus
tepi AC
3. Mari kita lukis garis lurus melalui
titik K dan P, kerana mereka berbaring
satu muka (DBC)
4. Segitiga MPK –
bahagian yang dikehendaki.

14.

Bina bahagian tetrahedron dengan satah,
melalui titik E, F, K.
D
1. Kami menjalankan KF.
2. Kami menjalankan FE.
3. Mari teruskan
EF, mari sambung AC.
F
4.EF AC =M
5. Kami laksanakan
MK.
E
M
AB=L
6.
MK
C
A
7. Menjalankan EL
L
EFKL – bahagian yang diperlukan
K
B

15.

Bina bahagian tetrahedron dengan satah,
melalui titik E, F, K
Yang mana satu
apa yang lurus
titik,
berbaring dalam
boleh
Sambung
yang terhasil
yang mana
mata
boleh
terus
itu
sama
tepi
boleh
teruskan,
kepada
dapatkan
mata,
berbohong
V
satu
sambung?
menyambung
menerima
tambahan
titik?
tepi,
nama
bahagian.
mata tambahan?
D
AC
ELFK
FSEC
dan satu titik
K, dan E
dan FK
F
L
C
M
A
E
K
B

16.

Bina bahagian
satah tetrahedron,
melepasi mata
E, F, K.
D
F
L
C
A
E
K
B
TENTANG

17.

Kesimpulan: tidak kira kaedah
bahagian pembinaan adalah sama

18. Pembinaan bahagian selari

19.

Tetrahedron mempunyai 6 muka
Segi tiga
Pentagon
Dalam bahagian-bahagiannya ia mungkin berubah
segi empat
Heksagon

20. Bina bahagian selari dengan satah melalui titik X selari dengan satah (OSV)

DALAM 1
A1
Y
X
D1
S
DALAM
A
D
Z
1. Mari jalani anda
C1
titik X garis lurus
selari dengan tepi
D1C1
2. Melalui titik X
langsung
selari dengan tepi
D1D
3. Melalui titik Z terdapat garis lurus
selari dengan tepi
DENGAN
DC
4. Mari kita lukis garis lurus melalui
mata S dan Y, kerana mereka berbaring
satu muka (BB1C1)
XYSZ – bahagian yang diperlukan

21.

Bina satu bahagian paip selari
satah yang melalui titik
M,A,D
DALAM 1
D1
E
A1
C1
DALAM
A
1. AD
2. MD
3. SAYA // AD, kerana (ABC)//(A1B1C1)
4. A.E.
5. AEMD - bahagian yang diperlukan
M
D
DENGAN

22. Bina keratan paip selari dengan satah melalui titik M, K, T

N
M
KEPADA
R
S
X
T

23. Selesaikan tugasan sendiri

m
T
Kepada
m
D
Kepada
T
Bina bahagian: a) saluran paip selari;
b) tetrahedron
satah yang melalui titik M, T, K.

24. Sumber yang digunakan

Soboleva L. I. Pembinaan bahagian
Tkacheva V.V. Pembinaan bahagian
tetrahedron dan parallelepiped
Gobozova L.V. Masalah pembinaan
bahagian
DVD. Pelajaran geometri daripada Kirill dan
Methodius. darjah 10, 2005
Tugas latihan dan ujian.
Geometri. Darjah 10 (Buku Nota)/Aleshina
T.N. – M.: Intellect-Center, 1998

Aksiom planimetri:

Dalam buku teks yang berbeza, sifat garis dan satah boleh dibentangkan dengan cara yang berbeza, dalam bentuk aksiom, akibat daripadanya, teorem, lemma, dll. Pertimbangkan buku teks oleh Pogorelov A.V.

Garis lurus membahagikan satah kepada dua satah separuh.

Dari mana-mana separuh garisan seseorang boleh memplot sudut dengan separuh satah tertentu ke dalam separuh satah tertentu. ukuran darjah, kurang daripada 180 0 , dan hanya satu.

Walau apa pun segi tiga, terdapat segi tiga sama di lokasi tertentu berbanding dengan setengah garisan tertentu.

Melalui titik yang tidak terletak pada garis tertentu, adalah mungkin untuk melukis pada satah paling banyak satu garis lurus selari dengan yang diberikan.

Aksiom stereometri:

Walau apa pun satah itu, ada mata yang tergolong dalam satah ini, dan mata yang bukan milik satah ini, dan mata yang bukan miliknya.

Jika dua satah berbeza mempunyai titik sepunya, maka ia bersilang di sepanjang garis lurus yang melalui titik ini.

Jika dua garis berbeza mempunyai titik sepunya, maka satah boleh dilukis melaluinya, dan hanya satu.

Walau apa pun garisan, ada titik yang tergolong dalam baris ini dan titik yang bukan miliknya.

Melalui mana-mana dua titik anda boleh melukis garis lurus, dan hanya satu.

Daripada tiga titik pada garisan, satu dan hanya satu terletak di antara dua yang lain.

Setiap segmen mempunyai panjang tertentu yang lebih besar daripada sifar. Panjang segmen adalah sama dengan jumlah panjang bahagian yang dibahagikan dengan mana-mana titiknya.

Garis lurus kepunyaan satah membahagikan satah ini kepada dua satah separuh.

Setiap sudut mempunyai ukuran darjah tertentu yang lebih besar daripada sifar. Sudut lurus ialah 180 0 . Ukuran darjah sudut adalah sama dengan jumlah ukuran darjah sudut yang mana ia dibahagikan dengan mana-mana sinar yang melalui antara sisinya.

Pada mana-mana separuh garisan dari titik permulaannya, anda boleh memplot segmen dengan panjang tertentu, dan hanya satu.

Daripada garis separuh pada satah yang mengandunginya, sudut dengan ukuran darjah tertentu kurang daripada 180 boleh diplot ke dalam satah separuh tertentu 0 , dan hanya satu.

Walau apa pun segi tiga itu, terdapat segi tiga sama dalam satah tertentu di lokasi tertentu berbanding dengan garis separuh tertentu dalam satah itu.

Pada satah, melalui titik tertentu yang tidak terletak pada garis tertentu, adalah mungkin untuk melukis paling banyak satu garis lurus selari dengan garis yang diberikan.

Bahagian

Di ruang angkasa, dua rajah, untuk kes kita satah dan polihedron, boleh mempunyai kedudukan relatif berikut: jangan bersilang, bersilang pada satu titik, bersilang dalam garis lurus dan satah bersilang polihedron di sepanjang bahagian dalamannya (Rajah 1) , dan pada masa yang sama membentuk angka berikut:

a) angka kosong (jangan bersilang)

b) titik

c) segmen

d) poligon

Jika terdapat poligon di persimpangan polihedron dan satah, maka poligon inidipanggil bahagian polihedron dengan satah .

Rajah 1

Definisi. Bahagian jasad spatial (contohnya, polihedron) ialah angka yang terhasil daripada persilangan badan dengan satah.

Memotong kapal terbang polihedron mari kita panggil mana-mana satah di kedua-dua belahnya yang terdapat titik polihedron yang diberikan.

Kami akan mempertimbangkan hanya kes apabila pesawat bersilang polihedron di sepanjang bahagian dalamannya. Dalam kes ini, persilangan satah ini dengan setiap muka polihedron akan menjadi segmen tertentu.

Jika satah bersilang dalam garis lurus, maka garis lurus itu dipanggilmengikuti salah satu pesawat ini ke yang lain.

Secara umum, satah pemotongan polihedron bersilang dengan satah setiap mukanya (serta mana-mana satah pemotongan polihedron ini). Ia juga bersilang setiap garisan di mana tepi polihedron terletak.

Garis lurus sepanjang satah pemotongan bersilang dengan satah mana-mana muka polihedron dipanggilmengikuti satah pemotongan pada satah muka ini, dan titik di mana satah pemotong memotong garisan yang mengandungi sebarang tepi polihedron dipanggilmengikuti satah pemotongan padagaris lurus ini. Titik ini juga merupakan kesan garisan pada satah pemotongan. Sekiranya satah pemotongan secara langsung bersilang dengan muka polihedron, maka kita boleh bercakap tentang jejak satah pemotongan pada muka, dan, begitu juga, tentangkesan satah pemotongan di pinggir polihedron, iaitu tentang kesan tepi pada satah pemotongan.

Oleh kerana garis lurus ditentukan secara unik oleh dua titik, untuk mencari kesan satah pemotongan pada mana-mana satah lain dan, khususnya, pada satah mana-mana muka polihedron, ia adalah mencukupi untuk membina dua titik sepunya satah.

Untuk membina jejak satah pemotongan, serta untuk membina bahagian polihedron dengan satah ini, bukan sahaja polihedron, tetapi juga satah pemotongan mesti dinyatakan. Dan pembinaan satah keratan bergantung kepada spesifikasi satah ini. Cara utama untuk menentukan satah, dan khususnya satah pemotongan, adalah seperti berikut:

tiga mata tidak terletak pada baris yang sama;

garis lurus dan titik tidak terletak di atasnya;

dua garis selari;

dua garis bersilang;

satu titik dan dua garis bersilang;

Cara lain untuk menentukan satah pemotongan juga boleh dilakukan.

Oleh itu, semua kaedah untuk membina bahagian polyhedra boleh dibahagikan kepada kaedah.

Kaedah untuk membina bahagian polyhedra

Kaedah bahagian polyhedra dalam stereometri digunakan dalam masalah pembinaan. Ia berdasarkan keupayaan untuk membina bahagian polihedron dan menentukan jenis bahagian.

Terdapat tiga kaedah utama untuk membina bahagian polyhedra:

Kaedah aksiomatik:

Kaedah jejak.

Kaedah gabungan.

Kaedah koordinat.

Catatan bahawa kaedah surih dan kaedah keratan tambahan adalah varietiKaedah aksiomatik untuk membina bahagian.

Kita juga boleh membezakan kaedah berikut untuk membina bahagian polyhedra:

membina bahagian polihedron dengan satah yang melalui titik tertentu selari dengan satah tertentu;

membina bahagian yang melalui garisan tertentu selari dengan garisan lain yang diberikan;

membina bahagian yang melalui titik tertentu selari dengan dua garis bersilang yang diberikan;

membina bahagian polihedron dengan satah yang melalui garisan tertentu berserenjang dengan satah tertentu;

membina keratan polihedron dengan satah yang melalui titik tertentu berserenjang dengan garis lurus tertentu.

Tindakan utama yang membentuk kaedah untuk membina bahagian ialah mencari titik persilangan garis dengan satah, membina garis persilangan dua satah, membina garis lurus selari dengan satah, berserenjang dengan satah. Untuk membina garis persilangan dua satah, dua titiknya biasanya ditemui dan garisan dilukis melaluinya. Untuk membina titik persilangan garis dan satah, cari garis dalam satah yang bersilang dengan yang diberi. Kemudian titik yang dikehendaki diperolehi di persimpangan garis yang dijumpai dengan yang diberikan.

Mari kita pertimbangkan secara berasingan yang telah kami senaraikankaedah untuk membina bahagian polyhedra:

Kaedah jejak.

Kaedah jejak adalah berdasarkan (berdasarkan) aksiom stereometri, intipati kaedah adalah untuk membina garis bantu, yang merupakan imej garis persilangan satah pemotongan dengan satah mana-mana muka rajah. Ia adalah paling mudah untuk membina imej garis persilangan satah pemotongan dengan satah tapak bawah. baris inidipanggil jejak utama satah pemotongan . Menggunakan surih, mudah untuk membina imej mata satah pemotongan yang terletak di tepi sisi atau muka rajah. Menghubungkan imej titik ini secara konsisten, kami memperoleh imej bahagian yang dikehendaki.

Perhatikan bahawa bahawa apabila membina surih utama satah pemotongan, pernyataan berikut digunakan.

Jika mata milik satah pemotongan dan tidak terletak pada garis lurus yang sama, dan unjuran mereka (tengah atau selari) ke atas satah dipilih sebagai satah utama, mata masing-masing maka titik persilangan garis yang sepadan, iaitu titik dan terletak pada garis yang sama (Rajah 1, a, b).

Rajah.1.a Rajah.1.b

Garis lurus ini adalah jejak utama satah pemotongan. Oleh kerana mata terletak pada jejak utama, untuk membinanya adalah cukup untuk mencari dua mata daripada ketiga-tiga ini.

Kaedah bahagian tambahan.

Kaedah membina bahagian polyhedra ini agak universal. Dalam kes di mana jejak (atau kesan) satah pemotongan yang dikehendaki berada di luar lukisan, kaedah ini malah mempunyai kelebihan tertentu. Pada masa yang sama, perlu diingat bahawa pembinaan yang dilakukan menggunakan kaedah ini sering menjadi "sesak". Walau bagaimanapun, dalam beberapa kes kaedah bahagian tambahan ternyata paling rasional.

Kaedah gabungan

Intipati kaedah gabungan untuk membina bahagian polyhedra ialah penggunaan teorem pada keselarian garis dan satah dalam ruang dalam kombinasi dengan kaedah aksiomatik.

Kaedah koordinat untuk membina bahagian.

Intipati kaedah koordinat adalah untuk mengira koordinat titik persilangan tepi atau polihedron dengan satah pemotongan, yang ditentukan oleh persamaan satah. Persamaan satah pemotongan dikira berdasarkan keadaan masalah.

Catatan , bahawa kaedah membina bahagian polihedron ini boleh diterima untuk komputer, kerana ia dikaitkan dengan sejumlah besar pengiraan dan oleh itu kaedah ini dinasihatkan untuk dilaksanakan menggunakan komputer.

Tugas utama kami adalah untuk membina bahagian polihedron dengan satah, i.e. dalam membina persilangan dua set ini.

Pembinaan bahagian polyhedra

Pertama sekali, kita perhatikan bahawa bahagian polihedron cembung ialah poligon rata cembung, bucunya, dalam kes umum, adalah titik persilangan satah pemotong dengan tepi polihedron, dan sisi dengannya. muka.

Contoh bahagian membina:

Kaedah untuk menentukan bahagian adalah sangat pelbagai. Yang paling biasa ialah kaedah menentukan satah pemotongan dengan tiga titik yang tidak terletak pada garis lurus yang sama.

Contoh 1. Untuk ABCDA saluran selari 1 B 1 C 1 D 1 . Bina bahagian yang melalui titik M, N, L.

Penyelesaian:

Sambungkan titik M dan L terletak pada satah AA 1 D 1 D.

Mari kita bersilang garis ML (kepunyaan bahagian) dengan tepi A 1 D 1 1 D 1 D. Dapatkan mata X 1 .

Titik X1 terletak di tepi A 1 D 1 , dan oleh itu pesawat A 1 B 1 C 1 D 1 , kami menyambungkannya dengan jahitan N yang terletak pada satah yang sama.

X 1 N bersilang tepi A 1 B 1 pada titik K.

Sambungkan titik K dan M terletak pada satah AA yang sama 1 B 1 B.

Mari kita cari garis lurus persilangan satah keratan dengan satah DD 1 C 1 C:

Mari kita bersilang garisan ML (kepunyaan bahagian) dengan tepi DD 1 , mereka terletak dalam satah AA yang sama 1 D 1 D, kita dapat titik X 2 .

Mari kita bersilang garis KN (kepunyaan bahagian) dengan tepi D 1 C 1 , mereka terletak pada satah A yang sama 1 B 1 C 1 D 1 , kita mendapat mata X3;

Titik X2 dan X3 terletak pada satah DD 1 C 1 C. Lukiskan garis lurus X 2 X 3 , yang bersilang tepi C 1 C pada titik T, dan tepi DC pada titik P. Dan sambungkan titik L dan P yang terletak dalam satah ABCD.

Oleh itu, masalah itu dianggap selesai jika semua segmen di mana satah bersilang dengan muka polihedron ditemui, itulah yang kami lakukan. MKNTPL - bahagian yang diperlukan.

Catatan. Masalah yang sama untuk membina bahagian ini boleh diselesaikan menggunakan sifat satah selari.

Daripada perkara di atas, anda boleh membuat algoritma (peraturan) untuk menyelesaikan masalah jenis ini.

Peraturan untuk membina bahagian polyhedra:

Contoh 2. DL, M

Mari kita selesaikan menggunakan kaedah aksiomatik:

Mari kita lukis satah bantuDKM, yang bersilang tepi AB dan BC pada titik E danF(kemajuan penyelesaian dalam Rajah 2.). Mari kita bina "jejak" CM bagi satah keratan pada satah tambahan ini, cari titik persilangan CM dan EF– titik P. Titik P, sepertiL, terletak pada satah ABC, dan adalah mungkin untuk melukis garis lurus sepanjang satah keratan bersilang dengan satah ABC ("jejak" bahagian dalam satah ABC).

Contoh 3. Pada tepi AB dan AD piramid MABCD, kita tentukan titik P dan Q, masing-masing, titik tengah tepi ini, dan pada tepi MC kita tentukan titik R. Mari kita bina bahagian piramid dengan satah yang melalui titik P, Q dan R.

Kami akan menjalankan penyelesaian menggunakan kaedah gabungan:

1). Jelaslah bahawa surih utama satah PQR ialah garis lurus PQ.

2). Mari kita cari titik K di mana satah MAC bersilang dengan garis lurus PQ. Titik K dan R tergolong dalam kedua-dua satah PQR dan satah MAC. Oleh itu, dengan melukis garis lurus KR, kita mendapat garis persilangan satah ini.

3). Mari cari titik N=AC BD, lukis garis lurus MN dan cari titik F=KR MN.

4). Titik F ialah titik sepunya bagi satah PQR dan MDB, iaitu satah-satah ini bersilang di sepanjang garis lurus yang melalui titik F. Walau bagaimanapun, sejak PQ - garis tengah segi tiga ABD, maka PQ adalah selari dengan BD, iaitu garis PQ adalah selari dengan satah MDB. Kemudian satah PQR yang melalui garis lurus PQ memotong satah MDB sepanjang garis lurus selari dengan garis lurus PQ, iaitu selari dengan dan lurus BD. Oleh itu, dalam satah MDB melalui titik F kita melukis garis selari dengan garis BD.

5). Pembinaan lanjut jelas daripada rajah. Akibatnya, kami memperoleh poligon PQD"RB" - bahagian yang dikehendaki

Mari kita pertimbangkan keratan rentas prisma itu untuk kesederhanaan, iaitu, kemudahan pemikiran logik, mari kita pertimbangkan bahagian kubus (Rajah 3.a):

nasi. 3.a

Bahagian prisma dengan satah selari dengan tepi sisi ialah segiempat selari. Khususnya, bahagian pepenjuru ialah segiempat selari (Rajah 4).

Def. Bahagian pepenjuru Sebuah prisma dipotong oleh satah yang melalui dua sisi sisi yang tidak mempunyai muka yang sama.

Poligon yang terhasil daripada keratan pepenjuru prisma ialah segiempat selari. Soalan tentang bilangan bahagian pepenjurun-prisma sudut adalah lebih sukar daripada soalan bilangan pepenjuru. Akan ada banyak bahagian kerana terdapat pepenjuru di pangkalan. Kita tahu bahawa prisma cembung mempunyai poligon cembung pada tapaknya, dan prisma cembungn-gon pepenjuru. Oleh itu, kita boleh mengatakan bahawa terdapat separuh daripada banyak bahagian pepenjuru sebagai pepenjuru.

Catatan: Apabila membina bahagian parallelepiped dalam rajah, seseorang harus mengambil kira hakikat bahawa jika satah pemotong memotong dua muka bertentangan di sepanjang beberapa segmen, maka segmen ini selari "oleh sifat parallelepiped, i.e. Muka bertentangan bagi parallelepiped adalah selari dan sama.”

Kami akan memberikan jawapan kepada soalan lazim:

Apakah poligon yang diperoleh apabila sebuah kubus dipotong oleh satah?

"segi tiga, segi empat, pentagon, heksagon."

Bolehkah kubus dipotong oleh satah menjadi heptagon? Bagaimana dengan oktagon?

"tak boleh".

3) Timbul persoalan: apakah bilangan sisi poligon terbesar yang diperoleh dengan memotong polihedron dengan satah?

Bilangan sisi poligon terbesar yang diperoleh dengan memotong polihedron dengan satah adalah sama dengan bilangan muka polihedron .

Contoh 3. Bina keratan rentas prisma A 1 B 1 C 1 D 1 ABCD oleh satah yang melalui tiga titik M, N, K.

Mari kita pertimbangkan kes lokasi titik M, N, K pada permukaan prisma (Rajah 5).

Pertimbangkan kes: B dalam kes ini jelas M1 = B1.

Pembinaan:

Contoh 4. Bina satu bahagian ABCDA berpaip selari 1 B 1 C 1 D 1 satah yang melalui titik M, N, P (titik ditunjukkan dalam lukisan (Rajah 6)).

Penyelesaian:

nasi. 6

Titik N dan P terletak pada satah keratan dan pada satah tapak bawah selari. Mari kita bina garis lurus yang melalui titik-titik ini. Garis lurus ini ialah kesan satah pemotongan ke atas satah tapak selari.

Mari kita teruskan garis lurus di sebelah mana AB bagi paip selari terletak. Garis AB dan NP bersilang pada satu titik S. Titik ini tergolong dalam satah keratan.

Oleh kerana titik M juga tergolong dalam satah keratan dan bersilang garis AA 1 pada satu ketika X.

Titik X dan N terletak pada satah muka AA yang sama 1 D 1 D, sambungkannya dan dapatkan garis lurus XN.

Oleh kerana satah muka selari adalah selari, maka melalui titik M kita boleh melukis garis lurus ke muka A 1 B 1 C 1 D 1 , selari dengan garis NP. Garis ini akan bersilang dengan sisi B 1 DENGAN 1 pada titik Y.

Begitu juga, kita melukis garis lurus YZ, selari dengan garis lurus XN. Kami menyambungkan Z dengan P dan dapatkan bahagian yang dikehendaki - MYZPNX.

Bahagian piramid oleh satah yang melalui puncaknya ialah segi tiga. Khususnya, segitiga adalah bahagian pepenjuru. Ini adalah bahagian oleh satah yang melalui dua tepi sisi piramid yang tidak bersebelahan.

Contoh 4. Bina satu bahagian piramid ABCDsatah melalui titik K,L, M.

Penyelesaian:

Mari kita selesaikan contoh yang sama ini secara berbeza .

Mari kita andaikan bahawa pada titik K,L, dan bahagian yang dibina MKLNM(Gamb. 7). Mari kita nyatakan denganFtitik persilangan pepenjuru segiempatKLNM. Jom buat directDFdan menandakan denganF 1 titik persilangannya dengan tepi ABC. titikF 1 bertepatan dengan titik persilangan garis lurus AM dan SC (F 1 pada masa yang sama kepunyaan pesawat AMDDanDSK). NoktahF 1 mudah dibina. Seterusnya kita membina satu titikFsebagai titik persimpanganDF 1 DanL.M.. Seterusnya kita temui maksudnyaN.

Teknik yang dipertimbangkan dipanggilkaedah reka bentuk dalaman . (Untuk kes kami kita bercakap tentang mengenai reka bentuk pusat. segi empatKMSA ialah unjuran segi empatKMNLdari titikD. Dalam kes ini, titik persilangan pepenjuruKMNL- titikF– pergi ke titik persilangan pepenjuru segi empatKMSA - titikF 1 .

Kawasan keratan polihedron.

Masalah pengiraan luas keratan rentas polihedron biasanya diselesaikan dalam beberapa peringkat. Jika masalah menyatakan bahawa bahagian telah dibina (atau satah pemotongan telah dilukis, dsb.), maka pada peringkat pertama penyelesaian jenis angka yang diperolehi dalam bahagian ditentukan.

Ini mesti dilakukan untuk memilih formula yang sesuai untuk mengira luas keratan rentas. Selepas jenis angka yang diperolehi dalam bahagian telah dijelaskan dan formula telah dipilih untuk mengira luas angka ini, kami meneruskan terus ke kerja pengiraan.

Dalam sesetengah kes, mungkin lebih mudah jika, tanpa memikirkan jenis angka yang diperolehi dalam bahagian itu, anda terus mengira luasnya menggunakan formula yang mengikuti daripada teorem.

Teorem mengenai luas unjuran ortogon poligon: Luas unjuran ortogon poligon pada satah adalah sama dengan hasil darab luasnya dan kosinus sudut antara satah poligon dan satah unjuran: .

Formula yang betul untuk mengira luas keratan ialah: di manakah luas unjuran ortogon rajah yang diperolehi dalam bahagian, dan ini adalah sudut antara satah pemotongan dan satah di mana rajah itu diunjurkan. Dengan penyelesaian ini, adalah perlu untuk membina unjuran ortogon bagi angka yang diperolehi dalam bahagian dan mengira

Jika penyataan masalah menyatakan bahawa bahagian perlu dibina dan luas bahagian yang terhasil mesti dijumpai, maka pada peringkat pertama seseorang harus secara wajar membina bahagian yang diberikan, dan kemudian, secara semula jadi, tentukan jenis angka yang diperolehi dalam bahagian, dsb.

Mari kita ambil perhatian fakta berikut: memandangkan bahagian polyhedra cembung dibina, poligon bahagian juga akan cembung, jadi luasnya boleh didapati dengan membahagikannya kepada segi tiga, iaitu, luas bahagian adalah sama dengan jumlah kawasan segi tiga dari mana ia tersusun.

Tugasan 1.

– piramid segi tiga sekata dengan sisi tapak sama dan ketinggian sama dengan Bina bahagian piramid dengan satah melalui titik di mana bahagian tengah sisi, dan cari luasnya (Rajah 8).

Penyelesaian.

Keratan rentas piramid ialah segi tiga. Jom cari kawasannya.

Oleh kerana tapak piramid ialah segi tiga sama sisi dan titiknya ialah titik tengah sisi, ia ialah ketinggian dan kemudian, .

Luas segi tiga boleh didapati:

Tugasan 2.

Tepi sisi prisma sekata adalah sama dengan sisi tapak. Bina bahagian prisma dengan satah melalui satu titikA, berserenjang dengan garis lurus Jika kita dapati luas keratan rentas prisma yang terhasil.

Penyelesaian.

Mari bina bahagian yang diberikan. Mari kita lakukan ini dari pertimbangan geometri semata-mata, sebagai contoh, seperti berikut.

Dalam satah yang melalui garis tertentu dan titik tertentu, lukiskan garis berserenjang dengan garis melalui titik ini (Rajah 9). Untuk tujuan ini, mari kita gunakan fakta bahawa dalam segi tiga iaitu mediannya juga ketinggian segi tiga ini. Jadi ia lurus.

Melalui titik itu kita melukis garis lain berserenjang dengan garis itu. Marilah kita melukisnya, sebagai contoh, dalam satah yang melalui garis lurus. Jelas bahawa garis ini adalah garis lurus

Jadi, dua garis bersilang dibina, berserenjang dengan garis. Garis-garis ini mentakrifkan satah yang melalui titik yang berserenjang dengan garis, iaitu, satah sekan ditentukan.

Mari kita bina bahagian prisma dengan satah ini. Perhatikan bahawa sejak, garis itu selari dengan satah. Kemudian satah yang melalui garis itu memotong satah sepanjang garis selari dengan garisan, iaitu garisan. Mari kita lukis garis lurus melalui titik dan sambungkan titik yang terhasil dengan titik.

Bahagian yang diberi segi empat. Mari tentukan kawasannya.