Med denne service kan du find den største og mindste værdi af en funktionén variabel f(x) med løsningen formateret i Word. Hvis funktionen f(x,y) er givet, er det derfor nødvendigt at finde yderpunktet for funktionen af ​​to variable. Du kan også finde intervallerne for stigende og faldende funktioner.

Find den største og mindste værdi af en funktion

y =

på segmentet [ ;]

Inkluder teori

Regler for indtastning af funktioner:

Nødvendig betingelse for ekstremum af en funktion af en variabel

Ligningen f" 0 (x *) = 0 er nødvendig betingelse ekstremum af en funktion af én variabel, dvs. ved punkt x * skal den første afledede af funktionen forsvinde. Det fremhæver stationære punkter x s, hvor funktionen ikke øges eller falder.

Tilstrækkelig betingelse for ekstremum af en funktion af én variabel

Lad f 0 (x) være to gange differentierbar med hensyn til x, der tilhører mængden D. Hvis betingelsen i punkt x * er opfyldt:

F" 0 (x *) = 0
f"" 0 (x *) > 0

Så er punkt x * det lokale (globale) minimumspunkt for funktionen.

Hvis betingelsen i punkt x * er opfyldt:

F" 0 (x *) = 0
f"" 0 (x *)< 0

Så er punkt x * et lokalt (globalt) maksimum.

Eksempel nr. 1. Find de største og mindste værdier af funktionen: på segmentet.
Løsning.

Det kritiske punkt er et x 1 = 2 (f'(x)=0). Dette punkt hører til segmentet. (Punkt x=0 er ikke kritisk, da 0∉).
Vi beregner værdierne af funktionen i enderne af segmentet og på det kritiske punkt.
f(1)=9, f(2)= 5/2, f(3)=3 8/81
Svar: f min = 5 / 2 ved x=2; fmax =9 ved x=1

Eksempel nr. 2. Brug højere ordens afledte, find ekstremum af funktionen y=x-2sin(x) .
Løsning.
Find den afledede af funktionen: y'=1-2cos(x) . Lad os finde de kritiske punkter: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Vi finder y’’=2sin(x), beregne , hvilket betyder x= π / 3 +2πk, k∈Z er minimumspunkterne for funktionen; , hvilket betyder x=- π / 3 +2πk, k∈Z er funktionens maksimumpunkter.

Eksempel nr. 3. Undersøg ekstremumfunktionen i nærheden af ​​punktet x=0.
Løsning. Her er det nødvendigt at finde yderpunkterne for funktionen. Hvis ekstremum x=0, så find ud af dens type (minimum eller maksimum). Hvis der blandt de fundne punkter ikke er x = 0, så beregn værdien af ​​funktionen f(x=0).
Det skal bemærkes, at når den afledede på hver side af et givet punkt ikke ændrer sit fortegn, er de mulige situationer ikke udtømte, selv for differentiable funktioner: det kan ske, at for et vilkårligt lille kvarter på den ene side af punktet x 0 eller på begge sider skifter den afledte fortegn. På disse punkter er det nødvendigt at bruge andre metoder til at studere funktioner på et ekstremum.

For at bestemme karakteren af ​​en funktion og tale om dens adfærd, er det nødvendigt at finde intervaller for stigning og fald. Denne proces kaldes funktionsforskning og graftegning. Ekstrempunktet bruges til at finde de største og mindste værdier af en funktion, da funktionen ved dem stiger eller falder fra intervallet.

Denne artikel afslører definitionerne, vi formulerer tilstrækkelig indikation stigning og fald på intervallet og betingelsen for eksistensen af ​​et ekstremum. Det gælder løsning af eksempler og problemer. Afsnittet om differentierende funktioner bør gentages, fordi løsningen skal bruge at finde den afledede.

Yandex.RTB R-A-339285-1 Definition 1

Funktionen y = f (x) vil stige i intervallet x, når uligheden f (x 2) > f (x 1) er opfyldt for enhver x 1 ∈ X og x 2 ∈ X, x 2 > x 1. Med andre ord svarer en større værdi af argumentet til en større værdi af funktionen.

Definition 2

Funktionen y = f (x) anses for at være aftagende på intervallet x, når, for enhver x 1 ∈ X, x 2 ∈ X, x 2 > x 1, ligheden f (x 2) > f (x 1) anses for sandt. Med andre ord svarer en større funktionsværdi til en mindre argumentværdi. Overvej figuren nedenfor.

Kommentar: Når funktionen er bestemt og kontinuert i enderne af intervallet med stigende og faldende, det vil sige (a; b), hvor x = a, x = b, indgår punkterne i intervallet for stigende og faldende. Dette er ikke i modstrid med definitionen; det betyder, at det foregår i intervallet x.

Grundlæggende egenskaber elementære funktioner type y = sin x - bestemthed og kontinuitet for reelle værdier af argumenterne. Herfra får vi, at sinus stiger over intervallet - π 2; π 2, så har stigningen på segmentet formen - π 2; π 2.

Definition 3

Punktet x 0 kaldes maksimum point for funktionen y = f (x), når for alle værdier af x er uligheden f (x 0) ≥ f (x) gyldig. Maksimal funktion er værdien af ​​funktionen i et punkt, og er angivet med y m a x .

Punktet x 0 kaldes minimumspunktet for funktionen y = f (x), når for alle værdier af x er uligheden f (x 0) ≤ f (x) gyldig. Minimum funktioner er værdien af ​​funktionen i et punkt, og har en betegnelse på formen y m i n .

Kvarter til punktet x 0 tages i betragtning ekstreme punkter, og værdien af ​​den funktion, der svarer til ekstremumpunkterne. Overvej figuren nedenfor.

Extrema af funktionen med den største og med laveste værdi funktioner. Overvej figuren nedenfor.

Den første figur siger, at det er nødvendigt at finde den største værdi af funktionen fra segmentet [a; b]. Det er fundet ved hjælp af maksimumpunkter og er lig med den maksimale værdi af funktionen, og det andet tal er mere som at finde maksimumpunktet ved x = b.

Tilstrækkelige betingelser for, at en funktion kan øges og falde

For at finde maksima og minima for en funktion er det nødvendigt at anvende tegn på ekstremum i det tilfælde, hvor funktionen opfylder disse betingelser. Det første tegn anses for at være det mest brugte.

Den første tilstrækkelige betingelse for et ekstremum

Definition 4

Lad en funktion y = f (x) være givet, som er differentierbar i et ε-kvarter til punktet x 0 og har kontinuitet i det givne punkt x 0. Det får vi herfra

• når f " (x) > 0 med x ∈ (x 0 - ε ; x 0) og f " (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• når f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 for x ∈ (x 0 ; x 0 + ε), så er x 0 minimumspunktet.

Med andre ord får vi deres betingelser for at sætte skiltet:

• når funktionen er kontinuert i punktet x 0, så har den en afledet med et skiftende fortegn, det vil sige fra + til -, hvilket betyder, at punktet kaldes et maksimum;
• når funktionen er kontinuert i punktet x 0, så har den en afledet med et skiftende fortegn fra - til +, hvilket betyder, at punktet kaldes et minimum.

For korrekt at bestemme maksimum- og minimumpunkterne for en funktion skal du følge algoritmen for at finde dem:

• find definitionsdomænet;
• find den afledede af funktionen på dette område;
• identificere nuller og punkter, hvor funktionen ikke eksisterer;
• bestemmelse af fortegn for den afledte på intervaller;
• vælg punkter, hvor funktionen skifter fortegn.

Lad os overveje algoritmen ved at løse flere eksempler på at finde ekstrema af en funktion.

Eksempel 1

Find maksimum- og minimumpunkterne for den givne funktion y = 2 (x + 1) 2 x - 2 .

Løsning

Omfanget af en given funktion er alt reelle tal undtagen x = 2. Lad os først finde den afledede af funktionen og få:

y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Herfra ser vi, at funktionens nuller er x = - 1, x = 5, x = 2, det vil sige, at hver parentes skal være lig med nul. Lad os markere det på talaksen og få:

Nu bestemmer vi fortegnene for den afledte fra hvert interval. Det er nødvendigt at vælge et punkt inkluderet i intervallet og erstatte det i udtrykket. For eksempel punkt x = - 2, x = 0, x = 3, x = 6.

Det forstår vi

y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, hvilket betyder, at intervallet - ∞ ; - 1 har en positiv afledet. Ligeledes finder vi, at

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Da det andet interval viste sig at være mindre end nul, betyder det, at den afledede på intervallet vil være negativ. Den tredje med minus, den fjerde med plus. For at bestemme kontinuitet skal du være opmærksom på den afledte fortegn; hvis det ændrer sig, er dette et ekstremumpunkt.

Vi finder, at i punktet x = - 1 vil funktionen være kontinuert, hvilket betyder, at den afledede vil skifte fortegn fra + til -. Ifølge det første tegn har vi, at x = - 1 er et maksimumpunkt, hvilket betyder, at vi får

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

Punktet x = 5 angiver, at funktionen er kontinuert, og den afledede vil skifte fortegn fra – til +. Dette betyder, at x = -1 er minimumspunktet, og dets bestemmelse har formen

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Grafisk billede

Svar: y m a x = y (- 1) = 0, y m i n = y (5) = 24.

Det er værd at være opmærksom på, at brugen af ​​det første tilstrækkelige kriterium for et ekstremum ikke kræver differentiabiliteten af ​​funktionen i punktet x 0, dette forenkler beregningen.

Eksempel 2

Find maksimum- og minimumpunkterne for funktionen y = 1 6 x 3 = 2 x 2 + 22 3 x - 8.

Løsning.

En funktions domæne er alle reelle tal. Dette kan skrives som et ligningssystem af formen:

1 6 x 3 - 2 x 2 - 22 3 x - 8, x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Så skal du finde den afledede:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 ", x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

Punktet x = 0 har ikke en afledt, fordi værdierne af de ensidige grænser er forskellige. Vi får det:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

Det følger, at funktionen er kontinuert i punktet x = 0, så regner vi

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 år (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

Det er nødvendigt at udføre beregninger for at finde værdien af ​​argumentet, når den afledede bliver nul:

1 2 x 2 - 4 x - 22 3, x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

Alle opnåede punkter skal markeres på en lige linje for at bestemme tegnet for hvert interval. Derfor er det nødvendigt at beregne den afledte ved vilkårlige punkter for hvert interval. For eksempel kan vi tage point med værdierne x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6. Det forstår vi

y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Billedet på den lige linje ser ud

Det betyder, at vi kommer til den konklusion, at det er nødvendigt at ty til det første tegn på et ekstremum. Lad os regne ud og finde det

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , herfra har de maksimale point værdierne x = - 4 + 2 3 3 , x = 4 - 2 3 3

Lad os gå videre til at beregne minimumsværdierne:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Lad os beregne funktionens maksima. Det forstår vi

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Grafisk billede

Svar:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 y a x 3 = y 4 - 2 3 3 = 8 27 3

Hvis en funktion f " (x 0) = 0 er givet, så hvis f "" (x 0) > 0, får vi, at x 0 er et minimumspunkt, hvis f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Eksempel 3

Find maksima og minima for funktionen y = 8 x x + 1.

Løsning

Først finder vi definitionsdomænet. Det forstår vi

D(y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Det er nødvendigt at differentiere funktionen, hvorefter vi får

y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

Ved x = 1 bliver den afledede nul, hvilket betyder, at punktet er et muligt ekstremum. For at afklare, er det nødvendigt at finde den anden afledede og beregne værdien ved x = 1. Vi får:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2 " x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0

Det betyder, at ved at bruge 2 tilstrækkelig betingelse for et ekstremum, opnår vi, at x = 1 er et maksimumspunkt. Ellers ser indtastningen ud som y m a x = y (1) = 8 1 1 + 1 = 4.

Grafisk billede

Svar: y m a x = y (1) = 4 ..

Definition 5

Funktionen y = f (x) har sin afledte op til n. orden i ε-kvarteret af et givet punkt x 0 og dens afledede op til n + 1. orden i punktet x 0 . Så f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Det følger heraf, at når n er et lige tal, så betragtes x 0 som et bøjningspunkt, når n er et ulige tal, så er x 0 et ekstremumpunkt, og f (n + 1) (x 0) > 0, så x 0 er et minimumspunkt, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.

Eksempel 4

Find maksimum- og minimumpunkterne for funktionen y y = 1 16 (x + 1) 3 (x - 3) 4.

Løsning

Den oprindelige funktion er en rationel hel funktion, hvilket betyder, at definitionsdomænet alle er reelle tal. Det er nødvendigt at differentiere funktionen. Det forstår vi

y " = 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Denne afledte vil gå til nul ved x 1 = - 1, x 2 = 5 7, x 3 = 3. Det vil sige, at punkterne kan være mulige ekstremumpunkter. Det er nødvendigt at anvende den tredje tilstrækkelige betingelse for ekstremum. At finde den anden afledede giver dig mulighed for nøjagtigt at bestemme tilstedeværelsen af ​​et maksimum og minimum af en funktion. Den anden afledede beregnes ved punkterne af dens mulige ekstremum. Det forstår vi

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

Det betyder, at x 2 = 5 7 er maksimumpunktet. Ved at anvende det 3. tilstrækkelige kriterium opnår vi, at for n = 1 og f (n + 1) 5 7< 0 .

Det er nødvendigt at bestemme karakteren af ​​punkterne x 1 = - 1, x 3 = 3. For at gøre dette skal du finde den tredje afledede og beregne værdierne på disse punkter. Det forstår vi

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Det betyder, at x 1 = - 1 er funktionens bøjningspunkt, da for n = 2 og f (n + 1) (- 1) ≠ 0. Det er nødvendigt at undersøge punktet x 3 = 3. For at gøre dette finder vi den 4. afledede og udfører beregninger på dette tidspunkt:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

Ud fra det, der blev besluttet ovenfor, konkluderer vi, at x 3 = 3 er minimumspunktet for funktionen.

Grafisk billede

Svar: x 2 = 5 7 er maksimumpunktet, x 3 = 3 er minimumspunktet for den givne funktion.

Hvis du bemærker en fejl i teksten, skal du markere den og trykke på Ctrl+Enter

>> Ekstrema

Funktionens ekstremum

Definition af ekstremum

Fungere y = f(x) kaldes stigende (faldende) i et bestemt interval, hvis for x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).

Hvis den differentiable funktion y = f (x) stiger (falder) på et interval, så er dens afledte på dette interval f " (x)> 0

(f"(x)< 0).

Prik x O hedder lokalt maksimumpunkt (minimum) funktion f (x), hvis der er et naboskab til punktet x o, for alle punkter, hvor uligheden f (x) er sand≤ f (x o) (f (x)≥ f (x o )).

Maksimum og minimum point kaldes ekstreme punkter, og værdierne af funktionen på disse punkter er dens ekstremer.

Ekstrempunkter

Nødvendige betingelser for et ekstremum . Hvis pointen x O er ekstremumpunktet for funktionen f (x), derefter enten f " (x o ) = 0 eller f(x o ) eksisterer ikke. Sådanne punkter kaldes kritisk, og selve funktionen er defineret på det kritiske punkt. En funktions yderpunkter bør søges blandt dens kritiske punkter.

Den første tilstrækkelige betingelse. Lade x O - kritisk punkt. hvis f" (x ) når du passerer gennem et punkt x O ændrer plustegnet til minus og derefter på punktet x o funktionen har et maksimum, ellers har den et minimum. Hvis den afledte, når den passerer gennem det kritiske punkt, ikke skifter fortegn, så ved punktet x O der er ingen ekstrem.

Anden tilstrækkelig betingelse. Lad funktionen f(x) have
f" (x ) i nærheden af ​​punktet x O og den anden afledede ved selve punktet x o. hvis f"(x o) = 0, >0 ( <0), то точка x o er det lokale minimum (maksimum) punkt for funktionen f (x). Hvis =0, så skal du enten bruge den første tilstrækkelige betingelse eller involvere højere.

På et segment kan funktionen y = f (x) nå sin minimums- eller maksimumværdi enten ved kritiske punkter eller i enderne af segmentet.

Eksempel 3.22.

Løsning. Fordi f " (

Problemer med at finde yderpunktet af en funktion

Eksempel 3.23. -en

Løsning. x Og y y
0 ≤ x≤
> 0, og hvornår x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение funktioner kv. enheder).

Eksempel 3.24. p ≈

Løsning. p s
S"
R = 2, H = 16/4 = 4.

Eksempel 3.22.Find yderpunkterne for funktionen f (x) = 2x 3 - 15x 2 + 36x - 14.

Løsning. Fordi f " (x ) = 6x 2 - 30x +36 = 6(x ​​​​-2)(x - 3), så de kritiske punkter for funktionen x 1 = 2 og x 2 = 3. Extrema kan kun være på disse punkter. Da den afledede, når den passerer gennem punktet x 1 = 2, skifter fortegn fra plus til minus, så har funktionen på dette tidspunkt et maksimum. Når man passerer gennem punktet x 2 = 3, ændrer den afledte fortegn fra minus til plus, så i punktet x 2 = 3 har funktionen et minimum. Efter at have beregnet funktionsværdierne ved punkterne
x 1 = 2 og x 2 = 3, finder vi yderpunkterne for funktionen: maksimum f (2) = 14 og minimum f (3) = 13.

Eksempel 3.23.Det er nødvendigt at bygge et rektangulært område nær stenmuren, så det er indhegnet på tre sider med trådnet, og den fjerde side støder op til muren. For dette er der -en lineære meter mesh. Ved hvilket billedformat vil webstedet have det største areal?

Løsning.Lad os betegne siderne af platformen med x Og y. Området på webstedet er S = xy. Lade y- dette er længden af ​​den side, der støder op til væggen. Så skal ligheden 2x + y = a efter betingelse være opfyldt. Derfor y = a - 2x og S = x (a - 2x), hvor
0 ≤ x≤ a /2 (områdets længde og bredde kan ikke være negativ). S " = a - 4x, a - 4x = 0 ved x = a/4, hvorfra
y = a - 2 x a/4 = a/2. Fordi x = a /4 er det eneste kritiske punkt; lad os kontrollere, om fortegnet for den afledte ændres, når vi passerer gennem dette punkt. Ved x a /4 S"> 0, og hvornår x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение funktioner S(a/4) = a/4(a - a/2) = a 2/8 (kv. enheder). Da S er kontinuerlig tændt, og dens værdier ved enderne S(0) og S(a /2) er lig med nul, vil den fundne værdi være højeste værdi funktioner. Således er det mest gunstige billedformat for webstedet under de givne betingelser for problemet y = 2x.

Eksempel 3.24.Det er nødvendigt at fremstille en lukket cylindrisk tank med en kapacitet på V=16 p ≈ 50 m 3. Hvad skal tankens dimensioner (radius R og højde H) være, så den mindste mængde materiale bruges til fremstillingen?

Løsning.Det samlede overfladeareal af cylinderen er S = 2 s R(R+H). Vi kender volumen af ​​cylinderen V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R2 = 16/R2. Så S(R) = 2 s (R2+16/R). Vi finder den afledede af denne funktion:
S"(R) = 2 p (2R-16/R2) = 4 p (R-8/R2). S" (R) = 0 ved R3 = 8, derfor,
R = 2, H = 16/4 = 4.

Stigende, faldende og ekstreme af en funktion

At finde intervallerne for stigning, fald og ekstrema for en funktion er både en selvstændig opgave og en væsentlig del af andre opgaver, især fuld funktionsstudie. Indledende information om stigning, fald og ekstrema af funktionen er givet i teoretisk kapitel om afledt, som jeg varmt anbefaler til forundersøgelse (eller gentagelse)– også af den grund, at følgende materiale er baseret på selve i det væsentlige afledt, være en harmonisk fortsættelse af denne artikel. Selvom tiden er knap, så er en rent formel praksis med eksempler fra dagens lektion også mulig.

Og i dag er der en sjælden enstemmighed i luften, og jeg kan direkte mærke, at alle tilstedeværende brænder af lyst lære at udforske en funktion ved hjælp af dens afledede. Derfor dukker der straks fornuftig, god, evig terminologi op på dine monitorskærme.

For hvad? En af grundene er den mest praktiske: så det er tydeligt, hvad der generelt kræves af dig i en bestemt opgave!

Monotonicitet af funktionen. Ekstrempunkter og yderpunkter for en funktion

Lad os overveje nogle funktioner. For at sige det enkelt antager vi, at hun sammenhængende på hele tallinjen:

For en sikkerheds skyld, lad os straks slippe af med mulige illusioner, især for de læsere, der for nylig har stiftet bekendtskab med intervaller af konstant fortegn for funktionen. Nu vi IKKE INTERESSERET, hvordan grafen for funktionen er placeret i forhold til aksen (over, under, hvor aksen skærer). For at være overbevisende skal du mentalt slette akserne og efterlade én graf. For det er der, interessen ligger.

Fungere stiger på et interval, hvis for to punkter i dette interval forbundet med relationen, er uligheden sand. Det er, større værdi argumentet svarer til en større værdi af funktionen, og dens graf går "fra bund til top". Demonstrationsfunktionen vokser over intervallet.

Ligeledes funktionen falder på et interval, hvis for enhver to punkter af et givet interval sådan, at uligheden er sand. Det vil sige, at en større værdi af argumentet svarer til en mindre værdi af funktionen, og dens graf går "fra top til bund." Vores funktion falder med intervaller .

Hvis en funktion øges eller falder over et interval, kaldes den strengt monotont i dette interval. Hvad er monotoni? Tag det bogstaveligt - monotoni.

Du kan også definere ikke faldende funktion (afslappet tilstand i den første definition) og ikke stigende funktion (blødgjort tilstand i 2. definition). En ikke-faldende eller ikke-stigende funktion på et interval kaldes monoton funktion i dette interval (streng monotoni er et specialtilfælde af "simpelthen" monotoni).

Teorien overvejer også andre tilgange til at bestemme stigningen/faldet af en funktion, herunder på halve intervaller, segmenter, men for ikke at hælde olie-olie-olie på dit hoved, vil vi aftale at operere med åbne intervaller med kategoriske definitioner - dette er tydeligere, og for at løse mange praktiske problemer ganske nok.

Dermed, i mine artikler vil formuleringen "en funktions monotonitet" næsten altid være skjult intervaller streng monotoni(strengt stigende eller strengt faldende funktion).

Et punkts naboskab. Ord, hvorefter eleverne stikker af, hvorhen de kan og gemmer sig forfærdet i krogene. ...Selvom efter indlægget Cauchy grænser De gemmer sig nok ikke længere, men gyser kun lidt =) Bare rolig, nu kommer der ingen beviser for matematisk analyses sætninger - jeg havde brug for omgivelserne til at formulere definitionerne mere stringent ekstreme punkter. Lad os huske:

Et punkts naboskab et interval, der indeholder et givet punkt, kaldes, og for nemheds skyld antages intervallet ofte at være symmetrisk. For eksempel et punkt og dets standardkvarter:

Faktisk er definitionerne:

Pointen hedder strenge maksimumspoint, hvis eksisterer hendes kvarter, for alle værdier, hvoraf, bortset fra selve punktet, uligheden. I vores konkret eksempel dette er pointen.

Pointen hedder strengt minimumspunkt, hvis eksisterer hendes kvarter, for alle værdier, hvoraf, bortset fra selve punktet, uligheden. På tegningen er der punkt "a".

Bemærk : kravet om nabolagssymmetri er slet ikke nødvendigt. Derudover er det vigtigt selve eksistensen kvarter (hvad enten det er lille eller mikroskopisk), der opfylder de angivne betingelser

Punkterne kaldes strengt ekstreme punkter eller simpelthen ekstreme punkter funktioner. Det vil sige, at det er en generaliseret betegnelse for maksimumpoint og minimumpoint.

Hvordan forstår vi ordet "ekstrem"? Ja, lige så direkte som monotoni. Ekstreme punkter i rutsjebaner.

Som i tilfældet med monotoni eksisterer løse postulater og er endnu mere almindelige i teorien (hvilket naturligvis de strenge sager, der overvejes, falder ind under!):

Pointen hedder maksimum point, hvis eksisterer dens omgivelser er sådan for alle
Pointen hedder minimumspunkt, hvis eksisterer dens omgivelser er sådan for alle værdierne i dette kvarter, holder uligheden.

Bemærk, at i henhold til de sidste to definitioner betragtes ethvert punkt i en konstant funktion (eller et "fladt udsnit" af en funktion) som både et maksimum og et minimumspunkt! Funktionen er i øvrigt både ikke-stigende og ikke-faldende, altså monoton. Disse overvejelser vil vi dog overlade til teoretikere, da vi i praksis næsten altid betragter traditionelle "bakker" og "huler" (se tegning) med en unik "bakkens konge" eller "sumpens prinsesse". Som en sort forekommer det tip, rettet op eller ned, for eksempel minimum af funktionen ved punktet.

Åh, og apropos royalty:
– betydningen hedder maksimum funktioner;
– betydningen hedder minimum funktioner.

Almindeligt navn - ekstremer funktioner.

Vær venligst forsigtig med dine ord!

Ekstrempunkter– disse er "X"-værdier.
Yderligheder– "spil" betydninger.

! Bemærk : nogle gange refererer de anførte termer til "X-Y"-punkterne, der ligger direkte på GRAFEN AF SELVE funktionen.

Hvor mange ekstrema kan en funktion have?

Ingen, 1, 2, 3, ... osv. til evighed. For eksempel har sinus uendeligt mange minima og maksima.

VIGTIG! Udtrykket "maksimal funktion" ikke identisk udtrykket "maksimal værdi af en funktion". Det er let at bemærke, at værdien kun er maksimal i et lokalt kvarter, og øverst til venstre er der "sejere kammerater". Ligeledes er "minimum af en funktion" ikke det samme som "minimumsværdi af en funktion", og på tegningen ser vi, at værdien kun er minimum i et bestemt område. I denne forbindelse kaldes ekstremumpunkter også lokale ekstreme punkter, og det ekstreme – lokale ekstremer. De går og vandrer i nærheden og global brødre. Så enhver parabel har i sit toppunkt globalt minimum eller globalt maksimum. Yderligere vil jeg ikke skelne mellem typer af ekstremer, og forklaringen er udtrykt mere til generelle pædagogiske formål - de yderligere adjektiver "lokal"/"global" bør ikke overraske dig.

Lad os opsummere vores lille udflugt ind i teorien med et testskud: hvad betyder opgaven "finde funktionens monotoniske intervaller og ekstremumpunkter"?

Ordlyden opfordrer dig til at finde:

– intervaller med stigende/faldende funktion (ikke-faldende, ikke-stigende forekommer meget sjældnere);

– maksimum- og/eller minimumspoint (hvis der findes). Nå, for at undgå fiasko, er det bedre at finde minimums/maksimum selv ;-)

Hvordan bestemmer man alt dette? Brug af afledte funktion!

Sådan finder du intervaller for stigende, faldende,
yderpunkter og yderpunkter for funktionen?

Mange regler er faktisk allerede kendt og forstået fra lektion om betydningen af ​​et derivat.

Tangent derivat bringer den glade nyhed, at funktionen er stigende hele vejen igennem definitionsdomæne.

Med cotangens og dets derivat situationen er stik modsat.

Arcsinen stiger over intervallet - den afledte her er positiv: .
Når funktionen er defineret, men ikke differentierbar. Men på det kritiske punkt er der en højrehåndet afledt og en højrehåndet tangent, og på den anden kant er der deres venstrehåndede modstykker.

Jeg tror, ​​det ikke vil være for svært for dig at udføre lignende ræsonnementer for arc cosinus og dens afledte.

Alle ovenstående sager, hvoraf mange er tabelformede derivater, jeg minder dig om, følg direkte fra afledte definitioner.

Hvorfor udforske en funktion ved hjælp af dens afledede?

For bedre at forstå, hvordan grafen for denne funktion ser ud: hvor den går "bottom up", hvor "top down", hvor den når minimum og maksimum (hvis den overhovedet når). Ikke alle funktioner er så simple – i de fleste tilfælde aner vi slet ikke om grafen for en bestemt funktion.

Det er tid til at gå videre til mere meningsfulde eksempler og overveje Algoritme til at finde intervaller for monotonitet og ekstrema for en funktion:

Eksempel 1

Find intervaller for stigning/fald og ekstrema for funktionen

Løsning:

1) Det første skridt er at finde domæne for en funktion, og noter også pausepunkterne (hvis de findes). I I dette tilfælde funktionen er kontinuerlig på hele tallinjen, og denne handling er til en vis grad formel. Men i en række tilfælde blusser alvorlige lidenskaber op her, så lad os behandle afsnittet uden foragt.

2) Det andet punkt i algoritmen skyldes

en nødvendig betingelse for et ekstremum:

Hvis der er et ekstremum på et punkt, eksisterer værdien enten ikke.

Forvirret over slutningen? Extremum af "modulus x"-funktionen .

Betingelsen er nødvendig, men ikke nok, og det modsatte er ikke altid sandt. Så det følger endnu ikke af ligheden, at funktionen når et maksimum eller minimum ved punkt . Klassisk eksempel allerede fremhævet ovenfor - dette er en kubisk parabel og dens kritiske punkt.

Men uanset hvad, så dikterer den nødvendige betingelse for et ekstremum behovet for at finde mistænkelige punkter. For at gøre dette skal du finde den afledede og løse ligningen:

I begyndelsen af ​​den første artikel om funktionsgrafer Jeg fortalte dig, hvordan du hurtigt bygger en parabel ved hjælp af et eksempel : "...vi tager den første afledede og sætter lig med nul: ...Altså løsningen på vores ligning: - det er på dette tidspunkt, at parablens toppunkt er placeret...". Nu tror jeg, alle forstår, hvorfor parablens toppunkt er placeret præcis på dette punkt =) Generelt burde vi starte med et lignende eksempel her, men det er for simpelt (selv for en tekande). Derudover er der en analog til allersidst i lektionen om afledet af en funktion. Lad os derfor øge graden:

Eksempel 2

Find intervaller for monotonitet og ekstrema af funktionen

Dette er et eksempel på selvstændig beslutning. Fuldstændig løsning og en omtrentlig endelig prøve af opgaven i slutningen af ​​lektionen.

Det længe ventede øjeblik for møde med fraktioneret-rationelle funktioner er ankommet:

Eksempel 3

Udforsk en funktion ved hjælp af den første afledede

Vær opmærksom på, hvor varierende en og samme opgave kan omformuleres.

Løsning:

1) Funktionen lider af uendelige diskontinuiteter på punkter.

2) Vi opdager kritiske punkter. Lad os finde den første afledede og sidestille den med nul:

Lad os løse ligningen. En brøk er nul, når dens tæller er nul:

Vi får således tre kritiske punkter:

3) Vi plotter ALLE detekterede punkter på tallinjen og interval metode vi definerer tegnene for DERIVATET:

Jeg minder dig om, at du skal tage et punkt i intervallet og beregne værdien af ​​den afledte ved det og bestemme dets tegn. Det er mere rentabelt ikke selv at tælle, men at "estimere" verbalt. Lad os for eksempel tage et punkt, der hører til intervallet, og udføre substitutionen: .

To "plus" og et "minus" giver derfor et "minus", hvilket betyder, at den afledede er negativ over hele intervallet.

Handlingen skal, som du forstår, udføres for hvert af de seks intervaller. Bemærk i øvrigt, at tællerfaktoren og nævneren er strengt positiv for ethvert punkt i ethvert interval, hvilket i høj grad forenkler opgaven.

Så den afledte fortalte os, at FUNKTIONEN SELV øges med og falder med. Det er praktisk at forbinde intervaller af samme type med join-ikonet.

På det tidspunkt når funktionen sit maksimum:
På det tidspunkt når funktionen et minimum:

Tænk over hvorfor du ikke skal genberegne den anden værdi ;-)

Når man passerer gennem et punkt, ændrer den afledede ikke fortegn, så funktionen har INTET EKSTREM der - den både faldt og forblev faldende.

! Lad os gentage vigtigt punkt : punkter betragtes ikke som kritiske - de indeholder en funktion ikke bestemt. Følgelig her I princippet kan der ikke være nogen ekstremer(selvom den afledede skifter fortegn).

Svar: funktionen øges med og falder med På det punkt, hvor maksimum af funktionen nås: , og på punktet – minimum: .

Kendskab til monotoniske intervaller og ekstrema, kombineret med etablerede asymptoter allerede giver en rigtig god idé om udseende funktionsgrafik. En person med gennemsnitlig træning er i stand til verbalt at bestemme, at grafen for en funktion har to lodrette asymptoter og en skrå asymptote. Her er vores helt:

Prøv igen at korrelere resultaterne af undersøgelsen med grafen for denne funktion.
Der er intet ekstremum på det kritiske punkt, men det er der grafbøjning(hvilket som regel sker i lignende tilfælde).

Eksempel 4

Find yderpunkterne af funktionen

Eksempel 5

Find monotoniske intervaller, maksima og minima for funktionen

…det er næsten som en slags "X i en terning"-ferie i dag....
Sååå, hvem i galleriet tilbød at drikke for dette? =)

Hver opgave har sine egne indholdsmæssige nuancer og tekniske finesser, som kommenteres i slutningen af ​​lektionen.

Overvej grafen for en kontinuerlig funktion y=f(x) vist på figuren.

Funktionsværdi i et punkt x 1 vil være større end funktionsværdierne ved alle nabopunkter både til venstre og til højre for x 1 . I dette tilfælde siger vi, at funktionen har på punktet x 1 maksimum. På punktet x Funktion 3 har åbenbart også et maksimum. Hvis vi overvejer pointen x 2, så er funktionsværdien i den mindre end alle naboværdier. I dette tilfælde siger vi, at funktionen har på punktet x 2 minimum. Ligeledes for sagen x 4 .

Fungere y=f(x) på punktet x 0 har maksimum, hvis værdien af ​​funktionen på dette tidspunkt er større end dens værdier på alle punkter i et interval, der indeholder punktet x 0, dvs. hvis der er en sådan naboskab af et punkt x 0, hvilket er for alle x≠x 0 , der hører til dette kvarter, holder uligheden f(x)<f(x 0 ) .

Fungere y=f(x) Det har minimum på punktet x 0 , hvis der er en sådan naboskab af et punkt x 0 , det er for alle x≠x 0, der hører til dette kvarter, holder uligheden f(x)>f(x 0.

De punkter, hvor funktionen når sit maksimum og minimum, kaldes ekstremumpunkter, og funktionens værdier i disse punkter kaldes ekstrema for funktionen.

Lad os være opmærksomme på, at en funktion defineret på et segment kun kan nå sit maksimum og minimum på punkter indeholdt i det betragtede segment.

Bemærk, at hvis en funktion har et maksimum på et punkt, betyder det ikke, at funktionen på det tidspunkt har den største værdi i hele definitionsdomænet. I figuren diskuteret ovenfor, funktionen ved punktet x 1 har et maksimum, selvom der er punkter, hvor funktionsværdierne er større end på punktet x 1 . I særdeleshed, f(x 1) < f(x 4) dvs. minimum af en funktion er større end maksimum. Af definitionen af ​​maksimum følger det kun, at dette er det mest stor betydning fungerer på punkter, der er tilstrækkelig tæt på maksimumpunktet.

Sætning 1. (Nødvendig betingelse for eksistensen af ​​et ekstremum.) Hvis den differentierbare funktion y=f(x) har på punktet x=x 0 ekstremum, så bliver dens afledte på dette tidspunkt nul.

Bevis. Lad, for en bestemthed, på punktet x 0-funktionen har et maksimum. Derefter, for tilstrækkeligt små trin Δ x vi har f(x 0 + Δ x) 0 ) , dvs. Men derefter

Indføring af disse uligheder til grænsen ved Δ x→ 0 og under hensyntagen til, at den afledte f "(x 0) eksisterer, og derfor afhænger grænsen til venstre ikke af, hvordan Δ x→ 0, får vi: ved Δ x → 0 – 0 f"(x 0) ≥ 0 a ved Δ x → 0 + 0 f"(x 0) ≤ 0. Siden f"(x 0) definerer et tal, så er disse to uligheder kun kompatible hvis f"(x 0) = 0.

Den gennemprøvede sætning siger, at maksimum- og minimumpunkterne kun kan være blandt de værdier af argumentet, hvor den afledede bliver nul.

Vi betragtede tilfældet, når en funktion har en afledt på alle punkter i et bestemt segment. Hvordan er situationen i tilfælde, hvor derivatet ikke eksisterer? Lad os se på eksempler.

Eksempler.

1. y=|x|.

   Funktionen har ingen afledet på punktet x=0 (på dette tidspunkt har grafen for funktionen ikke en defineret tangent), men på dette tidspunkt har funktionen et minimum, da y(0)=0, og for alle x≠ 0y > 0.



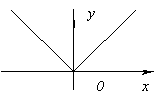
Funktionen har ingen afledt kl x=0, da det går til uendeligt kl x=0. Men på dette tidspunkt har funktionen et maksimum.



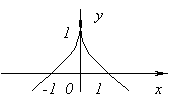
Funktionen har ingen afledt kl x=0, siden på x→0. På dette tidspunkt har funktionen hverken et maksimum eller et minimum. Virkelig, f(x)=0 og kl x<0f(x)<0, а при x>0f(x)>0.



Ud fra de givne eksempler og den formulerede sætning er det således klart, at en funktion kun kan have et ekstremum i to tilfælde: 1) på punkter, hvor den afledede eksisterer og er lig med nul; 2) på det punkt, hvor derivatet ikke eksisterer.

Dog hvis på et tidspunkt x 0 det ved vi f "(x 0 ) =0, så kan man ikke heraf slutte, at på punktet x 0 har funktionen et ekstremum.

For eksempel. .



Men punktum x=0 er ikke et ekstremumpunkt, da funktionsværdierne til venstre for dette punkt er placeret under aksen Okse, og til højre ovenfor.

Værdier af et argument fra domænet af en funktion, hvor den afledede af funktionen forsvinder eller ikke eksisterer, kaldes kritiske punkter.




Af alt ovenstående følger det, at funktionens ekstremumpunkter er blandt de kritiske punkter, og dog er ikke alle kritiske punkter et ekstremum. Derfor, for at finde yderpunktet for en funktion, skal du finde alle de kritiske punkter i funktionen og derefter undersøge hvert af disse punkter separat for maksimum og minimum. Følgende sætning tjener dette formål.

Sætning 2. (Tilstrækkelig betingelse for eksistensen af ​​et ekstremum.) Lad funktionen være kontinuerlig på et eller andet interval, der indeholder det kritiske punkt x 0, og er differentierbar på alle punkter i dette interval (undtagen måske selve punktet x 0). Hvis den afledte, når den bevæges fra venstre mod højre gennem dette punkt, skifter fortegn fra plus til minus, så i punktet x = x 0-funktionen har et maksimum. Hvis, når man passerer igennem x 0 fra venstre mod højre, den afledede skifter fortegn fra minus til plus, så har funktionen et minimum på dette tidspunkt.

Således, hvis

Bevis. Lad os først antage, at når vi passerer igennem x 0 skifter den afledte fortegn fra plus til minus, dvs. foran alle x, tæt på sagen x 0 f "(x)> 0 for x< x 0 , f "(x)< 0 for x>x 0 . Lad os anvende Lagranges sætning på forskellen f(x) - f(x 0 ) = f "(c)(x-x 0), hvor c ligger imellem x Og x 0 .

1. Lade x< x 0 . Derefter c< x 0 og f "(c)> 0. Derfor f "(c)(x-x 0)< 0 og derfor

   f(x) - f(x 0 )< 0, dvs. f(x)< f(x 0 ).

2. Lade x > x 0 . Derefter c>x 0 og f "(c)< 0. Midler f "(c)(x-x 0)< 0. Derfor f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Altså for alle værdier x tæt nok på x 0 f(x)< f(x 0 ) . Og det betyder, at på det tidspunkt x 0-funktionen har et maksimum.

Den anden del af minimumssætningen bevises på lignende måde.



Lad os illustrere betydningen af ​​denne sætning i figuren. Lade f "(x 1 ) =0 og for evt x, tæt nok på x 1, er ulighederne opfyldt

f "(x)< 0 kl x< x 1 , f "(x)> 0 kl x>x 1 .

Så til venstre for punktet x 1 funktionen øges og falder til højre, derfor når x = x 1 funktion går fra stigende til faldende, det vil sige, den har et maksimum.

På samme måde kan vi overveje punkter x 2 og x 3 .


Alt ovenstående kan skematisk afbildes på billedet:

Regel for at studere funktionen y=f(x) for ekstremum

1. Find domænet for en funktion f(x).
2. Find den første afledede af en funktion f "(x).
3. Bestem kritiske punkter for dette:
   1. find ligningens reelle rødder f "(x)=0;
   2. finde alle værdier x for hvilket derivatet f "(x) eksisterer ikke.
4. Bestem fortegnet for den afledede til venstre og højre for det kritiske punkt. Da fortegnet for den afledte forbliver konstant mellem to kritiske punkter, er det tilstrækkeligt at bestemme fortegnet for den afledte i et punkt til venstre og et punkt til højre for det kritiske punkt.
5. Beregn værdien af ​​funktionen ved ekstremumpunkterne.

Eksempler. Udforsk funktioner for minimum og maksimum.




MAKSIMUM OG MINDSTE VÆRDIER AF EN FUNKTION PÅ ET Segment

Den største værdien af ​​en funktion på et interval er den største af alle dens værdier på dette interval, og den mindste– den mindste af alle dens værdier.

Overvej funktionen y=f(x) kontinuerlig på segmentet [ a, b]. Som det er kendt, når en sådan funktion sine maksimum- og minimumværdier, enten ved segmentets grænse eller inde i det. Hvis den største eller mindste værdi af en funktion opnås ved et internt punkt i segmentet, så er denne værdi maksimum eller minimum af funktionen, det vil sige, den opnås på kritiske punkter.

Således får vi følgende regel for at finde de største og mindste værdier af en funktion på et segment[ a, b] :

1. Find alle kritiske punkter for funktionen i intervallet ( a, b) og beregn værdierne af funktionen på disse punkter.
2. Beregn værdierne af funktionen i enderne af segmentet hvornår x = a, x = b.
3. Fra alle de opnåede værdier skal du vælge den største og mindste.