Dengan perkhidmatan ini anda boleh cari nilai terbesar dan terkecil bagi sesuatu fungsi satu pembolehubah f(x) dengan penyelesaian diformatkan dalam Word. Jika fungsi f(x,y) diberikan, oleh itu, adalah perlu untuk mencari ekstrem bagi fungsi dua pembolehubah. Anda juga boleh mencari selang peningkatan dan penurunan fungsi.

Cari nilai terbesar dan terkecil bagi sesuatu fungsi

y =

pada segmen [ ;]

Sertakan teori

Peraturan untuk memasukkan fungsi:

Syarat yang diperlukan untuk ekstrem fungsi satu pembolehubah

Persamaan f" 0 (x *) = 0 ialah syarat yang perlu ekstrem bagi fungsi satu pembolehubah, i.e. pada titik x * terbitan pertama bagi fungsi mesti lenyap. Ia menyerlahkan titik pegun x s, di mana fungsi tidak bertambah atau berkurang.

Keadaan yang mencukupi untuk ekstrem fungsi satu pembolehubah

Biarkan f 0 (x) dua kali boleh dibezakan berkenaan dengan x kepunyaan set D. Jika pada titik x * syarat dipenuhi:

F" 0 (x *) = 0
f"" 0 (x *) > 0

Kemudian titik x * ialah titik minimum tempatan (global) bagi fungsi tersebut.

Jika pada titik x * syarat dipenuhi:

F" 0 (x *) = 0
f"" 0 (x *)< 0

Kemudian titik x * ialah maksimum tempatan (global).

Contoh No. 1. Cari nilai terbesar dan terkecil fungsi: pada segmen.
Penyelesaian.

Titik genting ialah satu x 1 = 2 (f’(x)=0). Titik ini tergolong dalam segmen. (Titik x=0 tidak kritikal, kerana 0∉).
Kami mengira nilai fungsi pada hujung segmen dan pada titik kritikal.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Jawapan: f min = 5 / 2 pada x=2; f maks =9 pada x=1

Contoh No. 2. Dengan menggunakan terbitan tertib tinggi, cari ekstrem bagi fungsi y=x-2sin(x) .
Penyelesaian.
Cari terbitan bagi fungsi: y’=1-2cos(x) . Mari cari titik genting: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Kami dapati y’’=2sin(x), hitung , yang bermaksud x= π / 3 +2πk, k∈Z ialah titik minimum bagi fungsi; , yang bermaksud x=- π / 3 +2πk, k∈Z ialah titik maksimum fungsi.

Contoh No. 3. Siasat fungsi ekstrem di sekitar titik x=0.
Penyelesaian. Di sini adalah perlu untuk mencari extrema fungsi. Jika extremum x=0, maka ketahui jenisnya (minimum atau maksimum). Jika antara titik yang ditemui tiada x = 0, maka hitung nilai fungsi f(x=0).
Perlu diingat bahawa apabila terbitan pada setiap sisi titik tertentu tidak mengubah tandanya, situasi yang mungkin tidak habis walaupun untuk fungsi yang boleh dibezakan: ia boleh berlaku bahawa untuk kejiranan kecil yang sewenang-wenangnya pada satu sisi titik x 0 atau pada kedua-dua belah tanda perubahan terbitan. Pada titik ini adalah perlu untuk menggunakan kaedah lain untuk mengkaji fungsi secara ekstrem.

Untuk menentukan sifat fungsi dan bercakap tentang kelakuannya, adalah perlu untuk mencari selang peningkatan dan penurunan. Proses ini dipanggil penyelidikan fungsi dan grafik. Titik ekstrem digunakan apabila mencari nilai terbesar dan terkecil fungsi, kerana pada mereka fungsi meningkat atau berkurangan daripada selang.

Artikel ini mendedahkan definisi, kami rumuskan petunjuk yang mencukupi peningkatan dan penurunan pada selang dan syarat untuk kewujudan ekstrem. Ini terpakai untuk menyelesaikan contoh dan masalah. Bahagian pada fungsi pembezaan harus diulang, kerana penyelesaiannya perlu menggunakan mencari derivatif.

Yandex.RTB R-A-339285-1 Definisi 1

Fungsi y = f (x) akan meningkat pada selang x apabila, bagi mana-mana x 1 ∈ X dan x 2 ∈ X, x 2 > x 1, ketaksamaan f (x 2) > f (x 1) dipenuhi. Dengan kata lain, nilai argumen yang lebih besar sepadan dengan nilai fungsi yang lebih besar.

Definisi 2

Fungsi y = f (x) dianggap berkurangan pada selang x apabila, untuk sebarang x 1 ∈ X, x 2 ∈ X, x 2 > x 1, kesamaan f (x 2) > f (x 1) dianggap benar. Dalam erti kata lain, nilai fungsi yang lebih besar sepadan dengan nilai hujah yang lebih kecil. Pertimbangkan rajah di bawah.

Ulasan: Apabila fungsi adalah pasti dan berterusan pada hujung selang peningkatan dan penurunan, iaitu (a; b), di mana x = a, x = b, titik-titik dimasukkan dalam selang peningkatan dan penurunan. Ini tidak bercanggah dengan definisi; ini bermakna ia berlaku pada selang x.

Sifat asas fungsi asas jenis y = sin x – kepastian dan kesinambungan untuk nilai sebenar hujah. Dari sini kita dapati bahawa sinus bertambah sepanjang selang - π 2; π 2, maka pertambahan pada segmen mempunyai bentuk - π 2; π 2.

Definisi 3

Titik x 0 dipanggil titik maksimum untuk fungsi y = f (x), apabila untuk semua nilai x ketaksamaan f (x 0) ≥ f (x) adalah sah. Fungsi maksimum ialah nilai fungsi pada satu titik, dan dilambangkan dengan y m a x .

Titik x 0 dipanggil titik minimum untuk fungsi y = f (x), apabila untuk semua nilai x ketaksamaan f (x 0) ≤ f (x) adalah sah. Fungsi minimum ialah nilai fungsi pada satu titik, dan mempunyai sebutan bentuk y m i n .

Kejiranan titik x 0 dipertimbangkan titik melampau, dan nilai fungsi yang sepadan dengan titik ekstrem. Pertimbangkan rajah di bawah.

Extrema fungsi dengan yang terbesar dan dengan nilai terendah fungsi. Pertimbangkan rajah di bawah.

Angka pertama mengatakan bahawa adalah perlu untuk mencari nilai terbesar fungsi daripada segmen [a; b] . Ia didapati menggunakan titik maksimum dan bersamaan dengan nilai maksimum fungsi, dan angka kedua lebih seperti mencari titik maksimum pada x = b.

Keadaan yang mencukupi untuk fungsi bertambah dan berkurang

Untuk mencari maksima dan minima fungsi, adalah perlu untuk menggunakan tanda ekstrem dalam kes apabila fungsi itu memenuhi syarat ini. Tanda pertama dianggap paling kerap digunakan.

Syarat pertama yang mencukupi untuk ekstrem

Definisi 4

Biarkan fungsi y = f (x) diberikan, yang boleh dibezakan dalam kejiranan ε titik x 0, dan mempunyai kesinambungan pada titik x 0 yang diberi. Dari sini kita dapat itu

• apabila f " (x) > 0 dengan x ∈ (x 0 - ε ; x 0) dan f " (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• apabila f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 untuk x ∈ (x 0 ; x 0 + ε), maka x 0 ialah titik minimum.

Dengan kata lain, kami memperoleh syarat mereka untuk menetapkan tanda:

• apabila fungsi itu selanjar pada titik x 0, maka ia mempunyai terbitan dengan tanda yang berubah, iaitu dari + ke -, yang bermaksud titik itu dipanggil maksimum;
• apabila fungsi selanjar pada titik x 0, maka ia mempunyai terbitan dengan tanda berubah dari - ke +, yang bermaksud titik itu dipanggil minimum.

Untuk menentukan titik maksimum dan minimum fungsi dengan betul, anda mesti mengikut algoritma untuk mencarinya:

• cari domain definisi;
• cari terbitan bagi fungsi pada kawasan ini;
• mengenal pasti sifar dan titik di mana fungsi tidak wujud;
• menentukan tanda terbitan pada selang waktu;
• pilih titik di mana fungsi bertukar tanda.

Mari kita pertimbangkan algoritma dengan menyelesaikan beberapa contoh mencari ekstrem fungsi.

Contoh 1

Cari titik maksimum dan minimum bagi fungsi yang diberi y = 2 (x + 1) 2 x - 2 .

Penyelesaian

Skop fungsi yang diberikan adalah segala-galanya nombor nyata kecuali x = 2. Mula-mula, mari cari derivatif fungsi dan dapatkan:

y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2 ) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Dari sini kita melihat bahawa sifar fungsi ialah x = - 1, x = 5, x = 2, iaitu setiap kurungan mesti disamakan dengan sifar. Mari tandakannya pada paksi nombor dan dapatkan:

Sekarang kita tentukan tanda-tanda derivatif dari setiap selang. Ia adalah perlu untuk memilih titik yang termasuk dalam selang dan menggantikannya ke dalam ungkapan. Contohnya, titik x = - 2, x = 0, x = 3, x = 6.

Kami dapat itu

y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, yang bermaksud selang - ∞ ; - 1 mempunyai terbitan positif. Begitu juga, kita dapati bahawa

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Memandangkan selang kedua ternyata kurang daripada sifar, ini bermakna derivatif pada selang itu akan menjadi negatif. Yang ketiga dengan tolak, yang keempat dengan tambah. Untuk menentukan kesinambungan, anda perlu memberi perhatian kepada tanda derivatif; jika ia berubah, maka ini adalah titik ekstrem.

Kami mendapati bahawa pada titik x = - 1 fungsi akan berterusan, yang bermaksud bahawa terbitan akan menukar tanda dari + kepada -. Menurut tanda pertama, kita mempunyai bahawa x = - 1 ialah titik maksimum, yang bermaksud kita mendapat

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

Titik x = 5 menunjukkan bahawa fungsi itu berterusan, dan terbitan akan menukar tanda dari – kepada +. Ini bermakna bahawa x = -1 ialah titik minimum, dan penentuannya mempunyai bentuk

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Imej grafik

Jawapan: y m a x = y (- 1) = 0, y m i n = y (5) = 24.

Perlu diberi perhatian kepada fakta bahawa penggunaan kriteria pertama yang mencukupi untuk ekstrem tidak memerlukan kebolehbezaan fungsi pada titik x 0, ini memudahkan pengiraan.

Contoh 2

Cari titik maksimum dan minimum bagi fungsi y = 1 6 x 3 = 2 x 2 + 22 3 x - 8.

Penyelesaian.

Domain fungsi ialah semua nombor nyata. Ini boleh ditulis sebagai sistem persamaan dalam bentuk:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Kemudian anda perlu mencari derivatif:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

Titik x = 0 tidak mempunyai derivatif, kerana nilai-nilai had satu sisi adalah berbeza. Kami mendapat bahawa:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

Ia berikutan bahawa fungsi adalah selanjar pada titik x = 0, maka kita mengira

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

Ia adalah perlu untuk melakukan pengiraan untuk mencari nilai hujah apabila terbitan menjadi sifar:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

Semua mata yang diperoleh mesti ditanda pada garis lurus untuk menentukan tanda setiap selang. Oleh itu, adalah perlu untuk mengira derivatif pada titik arbitrari untuk setiap selang. Sebagai contoh, kita boleh mengambil mata dengan nilai x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6. Kami dapat itu

y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Imej pada garis lurus kelihatan seperti

Ini bermakna kita sampai pada kesimpulan bahawa adalah perlu untuk menggunakan tanda pertama extremum. Marilah kita mengira dan mencarinya

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , maka dari sini titik maksimum mempunyai nilai x = - 4 + 2 3 3 , x = 4 - 2 3 3

Mari kita teruskan untuk mengira minimum:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Mari kita hitung maksima fungsi tersebut. Kami dapat itu

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Imej grafik

Jawapan:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 x 3 y m = y 4 - 2 3 3 = 8 27 3

Jika fungsi f " (x 0) = 0 diberikan, maka jika f "" (x 0) > 0, kita memperoleh bahawa x 0 ialah titik minimum jika f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Contoh 3

Cari maksima dan minima bagi fungsi y = 8 x x + 1.

Penyelesaian

Pertama, kita mencari domain definisi. Kami dapat itu

D(y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Ia adalah perlu untuk membezakan fungsi, selepas itu kita dapat

y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

Pada x = 1, derivatif menjadi sifar, yang bermaksud bahawa titik adalah ekstrem yang mungkin. Untuk menjelaskan, adalah perlu untuk mencari derivatif kedua dan mengira nilai pada x = 1. Kita mendapatkan:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0

Ini bermakna dengan menggunakan 2 keadaan yang mencukupi untuk ekstrem, kita memperoleh bahawa x = 1 ialah titik maksimum. Jika tidak, entri kelihatan seperti y m a x = y (1) = 8 1 1 + 1 = 4.

Imej grafik

Jawapan: y m a x = y (1) = 4 ..

Definisi 5

Fungsi y = f (x) mempunyai terbitannya sehingga tertib ke-n dalam kejiranan ε bagi titik x 0 tertentu dan terbitannya sehingga tertib n + 1 pada titik x 0 . Kemudian f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Ia berikutan bahawa apabila n ialah nombor genap, maka x 0 dianggap sebagai titik infleksi, apabila n ialah nombor ganjil, maka x 0 ialah titik ekstrem, dan f (n + 1) (x 0) > 0, maka x 0 ialah titik minimum, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.

Contoh 4

Cari titik maksimum dan minimum bagi fungsi y y = 1 16 (x + 1) 3 (x - 3) 4.

Penyelesaian

Fungsi asal ialah keseluruhan fungsi rasional, yang bermaksud bahawa domain definisi adalah semua nombor nyata. Ia adalah perlu untuk membezakan fungsi. Kami dapat itu

y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4" = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Derivatif ini akan pergi ke sifar pada x 1 = - 1, x 2 = 5 7, x 3 = 3. Iaitu, mata boleh menjadi titik ekstrem yang mungkin. Ia adalah perlu untuk memohon syarat ketiga yang mencukupi untuk ekstrem. Mencari derivatif kedua membolehkan anda menentukan dengan tepat kehadiran maksimum dan minimum fungsi. Derivatif kedua dikira pada titik ekstrem yang mungkin. Kami dapat itu

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

Ini bermakna x 2 = 5 7 ialah titik maksimum. Menggunakan kriteria mencukupi ke-3, kita memperoleh bahawa untuk n = 1 dan f (n + 1) 5 7< 0 .

Ia adalah perlu untuk menentukan sifat titik x 1 = - 1, x 3 = 3. Untuk melakukan ini, anda perlu mencari derivatif ketiga dan mengira nilai pada titik ini. Kami dapat itu

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Ini bermakna x 1 = - 1 ialah titik infleksi fungsi, kerana untuk n = 2 dan f (n + 1) (- 1) ≠ 0. Adalah perlu untuk menyiasat titik x 3 = 3. Untuk melakukan ini, kami mencari terbitan ke-4 dan melakukan pengiraan pada ketika ini:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

Daripada apa yang telah diputuskan di atas kita membuat kesimpulan bahawa x 3 = 3 ialah titik minimum fungsi.

Imej grafik

Jawapan: x 2 = 5 7 ialah titik maksimum, x 3 = 3 ialah titik minimum bagi fungsi yang diberikan.

Jika anda melihat ralat dalam teks, sila serlahkannya dan tekan Ctrl+Enter

>>Melampau

Ekstrem fungsi

Definisi extremum

Fungsi y = f(x) dipanggil semakin meningkat (semakin berkurangan) dalam selang waktu tertentu, jika untuk x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).

Jika fungsi boleh beza y = f (x) bertambah (berkurang) pada selang, maka terbitannya pada selang ini f " (x)> 0

(f"(x)< 0).

titik x O dipanggil titik maksimum tempatan (minimum) fungsi f (x) jika terdapat kejiranan titik x o, untuk semua titik yang ketaksamaan f (x) adalah benar≤ f (x o ) (f (x )≥ f (x o )).

Mata maksimum dan minimum dipanggil titik melampau, dan nilai fungsi pada titik ini adalah melampau.

Titik melampau

Syarat yang diperlukan untuk ekstrem . Jika titik x O ialah titik ekstrem bagi fungsi f (x), maka sama ada f " (x o ) = 0, atau f(x o ) tidak wujud. Titik sedemikian dipanggil kritikal, dan fungsi itu sendiri ditakrifkan pada titik kritikal. Ekstrema fungsi harus dicari di antara titik kritikalnya.

Syarat pertama yang mencukupi. biarlah x O - titik kritikal. jika f" (x ) apabila melalui suatu titik x O menukar tanda tambah kepada tolak, kemudian pada titik x o fungsi mempunyai maksimum, jika tidak, ia mempunyai minimum. Jika, apabila melalui titik kritikal, derivatif tidak berubah tanda, maka pada titik x O tidak ada yang melampau.

Syarat kedua yang mencukupi. Biarkan fungsi f(x) mempunyai
f" (x ) di sekitar titik itu x O dan terbitan kedua pada titik itu sendiri x o. jika f"(x o) = 0, >0 ( <0), то точка x o ialah titik minimum (maksimum) setempat bagi fungsi f (x). Jika =0, ​​maka anda perlu sama ada menggunakan syarat mencukupi pertama atau melibatkan yang lebih tinggi.

Pada segmen, fungsi y = f (x) boleh mencapai nilai minimum atau maksimumnya sama ada pada titik kritikal atau di hujung segmen.

Contoh 3.22.

Penyelesaian. Kerana f " (

Masalah mencari ekstrem fungsi

Contoh 3.23. a

Penyelesaian. x Dan y y
0 ≤ x≤
> 0, dan bila x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение fungsi kv. unit).

Contoh 3.24. p ≈

Penyelesaian. p p
S"
R = 2, H = 16/4 = 4.

Contoh 3.22.Cari ekstrem bagi fungsi f (x) = 2x 3 - 15x 2 + 36x - 14.

Penyelesaian. Kerana f " (x ) = 6x 2 - 30x +36 = 6(x ​​​​-2)(x - 3), maka titik genting bagi fungsi x 1 = 2 dan x 2 = 3. Extrema hanya boleh berada pada titik ini. Oleh kerana apabila melalui titik x 1 = 2 derivatif berubah tanda dari tambah kepada tolak, maka pada ketika ini fungsi mempunyai maksimum. Apabila melalui titik x 2 = 3, derivatif menukar tandanya daripada tolak kepada tambah, jadi pada titik x 2 = 3 fungsi mempunyai minimum. Setelah mengira nilai fungsi pada titik
x 1 = 2 dan x 2 = 3, kita dapati ekstrem fungsi: maksimum f (2) = 14 dan minimum f (3) = 13.

Contoh 3.23.Ia adalah perlu untuk membina kawasan segi empat tepat berhampiran dinding batu supaya ia dipagari pada tiga sisi dengan dawai, dan sisi keempat bersebelahan dengan dinding. Untuk ini ada a meter linear mesh. Pada nisbah aspek apakah tapak tersebut mempunyai keluasan terbesar?

Penyelesaian.Mari kita nyatakan sisi platform dengan x Dan y. Luas tapak ialah S = xy. biarlah y- ini ialah panjang sisi yang bersebelahan dengan dinding. Kemudian, dengan syarat, kesamaan 2x + y = a mesti dipenuhi. Oleh itu y = a - 2x dan S = x (a - 2x), di mana
0 ≤ x≤ a /2 (panjang dan lebar kawasan tidak boleh negatif). S " = a - 4x, a - 4x = 0 pada x = a/4, dari mana
y = a - 2 × a/4 =a/2. Kerana ia x = a /4 ialah satu-satunya titik kritikal; mari kita semak sama ada tanda derivatif berubah apabila melalui titik ini. Pada x a /4 S"> 0, dan bila x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение fungsi S(a/4) = a/4(a - a/2) = a 2/8 (kv. unit). Oleh kerana S berterusan dan nilainya di hujung S(0) dan S(a /2) adalah sama dengan sifar, maka nilai yang ditemui ialah nilai tertinggi fungsi. Oleh itu, nisbah aspek yang paling baik bagi tapak di bawah keadaan masalah yang diberikan ialah y = 2x.

Contoh 3.24.Ia dikehendaki mengeluarkan tangki silinder tertutup dengan kapasiti V=16 p ≈ 50 m 3. Apakah dimensi tangki yang sepatutnya (jejari R dan ketinggian H) supaya jumlah bahan yang paling sedikit digunakan untuk pembuatannya?

Penyelesaian.Jumlah luas permukaan silinder ialah S = 2 hlm R(R+H). Kita tahu isipadu silinder V = p R 2 Н Þ Н = V/ p R 2 =16 p / h R2 = 16/R2. Jadi S(R) = 2 hlm (R 2 +16/R). Kami mencari terbitan fungsi ini:
S"(R) = 2 p (2R- 16/R 2) = 4 p (R- 8/R 2). S" (R) = 0 pada R 3 = 8, oleh itu,
R = 2, H = 16/4 = 4.

Bertambah, menurun dan melampau sesuatu fungsi

Mencari selang peningkatan, penurunan dan keterlaluan fungsi ialah tugas bebas dan bahagian penting tugas lain, khususnya, kajian fungsi penuh. Maklumat awal tentang peningkatan, penurunan dan ekstrem fungsi diberikan dalam bab teori terbitan, yang saya sangat mengesyorkan untuk kajian awal (atau pengulangan)– juga atas sebab bahan berikut adalah berdasarkan sangat pada dasarnya derivatif, menjadi kesinambungan harmoni artikel ini. Walaupun, jika masa adalah singkat, maka amalan formal semata-mata contoh dari pelajaran hari ini juga mungkin.

Dan hari ini terdapat semangat bersatu yang jarang berlaku di udara, dan saya secara langsung dapat merasakan bahawa semua orang yang hadir membara dengan keinginan belajar untuk meneroka fungsi menggunakan terbitannya. Oleh itu, istilah yang munasabah, baik, kekal serta-merta muncul pada skrin monitor anda.

Untuk apa? Salah satu sebabnya adalah yang paling praktikal: supaya jelas apa yang secara amnya diperlukan daripada anda dalam tugas tertentu!

Kemonotonan fungsi. Titik ekstrem dan ekstrem fungsi

Mari kita pertimbangkan beberapa fungsi. Ringkasnya, kami menganggap bahawa dia berterusan pada keseluruhan garis nombor:

Untuk berjaga-jaga, mari kita segera singkirkan kemungkinan ilusi, terutamanya bagi pembaca yang baru mengenali selang tanda tetap fungsi. Sekarang kita TIDAK BERMINAT, bagaimana graf fungsi terletak relatif kepada paksi (di atas, di bawah, tempat paksi bersilang). Untuk meyakinkan, padamkan paksi secara mental dan tinggalkan satu graf. Kerana di situlah letak minat.

Fungsi bertambah pada selang jika bagi mana-mana dua titik selang ini disambungkan oleh hubungan , ketaksamaan adalah benar. Itu dia, nilai yang lebih besar hujah sepadan dengan nilai fungsi yang lebih besar, dan grafnya pergi "dari bawah ke atas". Fungsi demonstrasi berkembang sepanjang selang waktu.

Begitu juga, fungsi berkurangan pada selang jika bagi mana-mana dua titik selang tertentu supaya , ketaksamaan adalah benar. Iaitu, nilai argumen yang lebih besar sepadan dengan nilai fungsi yang lebih kecil, dan grafnya pergi "dari atas ke bawah." Fungsi kami berkurangan pada selang waktu .

Jika fungsi bertambah atau berkurang dalam selang waktu, maka ia dipanggil benar-benar monoton pada selang ini. Apakah monotoni? Ambil secara literal - monotoni.

Anda juga boleh menentukan tidak berkurangan fungsi (keadaan santai dalam definisi pertama) dan tidak meningkat fungsi (keadaan lembut dalam definisi ke-2). Fungsi tidak berkurang atau tidak bertambah pada selang waktu dipanggil fungsi monotonik pada selang ini (kemonotoni ketat ialah kes khas kemonotoni "semata-mata").

Teori ini juga mempertimbangkan pendekatan lain untuk menentukan peningkatan/penurunan fungsi, termasuk pada separuh selang, segmen, tetapi untuk tidak mencurahkan minyak-minyak-minyak pada kepala anda, kami akan bersetuju untuk beroperasi dengan selang terbuka dengan definisi kategorikal - ini lebih jelas, dan cukup untuk menyelesaikan banyak masalah praktikal.

Oleh itu, dalam artikel saya perkataan "kemonotonan fungsi" hampir selalu disembunyikan selang waktu monotoni yang ketat(fungsi meningkat atau menurun dengan ketat).

Kejiranan satu titik. Kata-kata selepas itu pelajar melarikan diri ke mana sahaja mereka boleh dan bersembunyi dengan ngeri di sudut. ...Walaupun selepas pos Had Cauchy Mereka mungkin tidak lagi bersembunyi, tetapi hanya menggigil sedikit =) Jangan risau, kini tidak akan ada bukti teorem analisis matematik - Saya memerlukan persekitaran untuk merumuskan definisi dengan lebih ketat titik melampau. Mari kita ingat:

Kejiranan satu titik selang yang mengandungi titik tertentu dipanggil, dan untuk kemudahan selang itu sering diandaikan sebagai simetri. Sebagai contoh, titik dan kejiranan standardnya:

Sebenarnya, definisi:

Intinya dipanggil titik maksimum yang ketat, Jika wujud kejiranan dia, untuk semua nilai yang, kecuali untuk titik itu sendiri, ketaksamaan . Dalam kami contoh khusus inilah intinya.

Intinya dipanggil titik minimum yang ketat, Jika wujud kejiranan dia, untuk semua nilai yang, kecuali untuk titik itu sendiri, ketaksamaan . Dalam lukisan terdapat titik "a".

Catatan : keperluan simetri kejiranan tidak diperlukan sama sekali. Di samping itu, ia adalah penting hakikat kewujudan kejiranan (sama ada kecil atau mikroskopik) yang memenuhi syarat yang ditetapkan

Titik dipanggil titik ekstrem yang ketat atau secara ringkas titik melampau fungsi. Iaitu, ia adalah istilah umum untuk mata maksimum dan mata minimum.

Bagaimanakah kita memahami perkataan "melampau"? Ya, sama langsung dengan monotoni. Titik melampau roller coaster.

Seperti dalam kes monotoni, postulat longgar wujud dan lebih biasa dalam teori (yang, sudah tentu, kes-kes ketat yang dianggap jatuh di bawah!):

Intinya dipanggil titik maksimum, Jika wujud persekitarannya begitu untuk semua
Intinya dipanggil titik minimum, Jika wujud persekitarannya begitu untuk semua nilai kejiranan ini, ketidaksamaan itu berlaku.

Ambil perhatian bahawa mengikut dua takrifan terakhir, mana-mana titik fungsi malar (atau "bahagian rata" fungsi) dianggap sebagai titik maksimum dan minimum! Fungsi, dengan cara, adalah kedua-dua tidak meningkat dan tidak berkurang, iaitu, monotonik. Walau bagaimanapun, kami akan menyerahkan pertimbangan ini kepada ahli teori, kerana dalam praktiknya kami hampir selalu merenungkan "bukit" dan "lubang" tradisional (lihat lukisan) dengan "raja bukit" atau "puteri paya" yang unik. Sebagai pelbagai, ia berlaku tip, diarahkan ke atas atau ke bawah, sebagai contoh, minimum fungsi pada titik.

Oh, dan bercakap tentang royalti:
– maksudnya dipanggil maksimum fungsi;
– maksudnya dipanggil minimum fungsi.

Nama yang selalu digunakan - melampau fungsi.

Sila berhati-hati dengan kata-kata anda!

Titik melampau– ini ialah nilai “X”.
Melampau– makna “permainan”.

! Catatan : kadangkala istilah yang disenaraikan merujuk kepada titik "X-Y" yang terletak terus pada GRAF fungsi itu SENDIRI.

Berapakah bilangan ekstrem yang boleh dimiliki oleh sesuatu fungsi?

Tiada, 1, 2, 3, ... dsb. ke Infiniti. Contohnya, sinus mempunyai banyak minima dan maksimum.

PENTING! Istilah "fungsi maksimum" tidak serupa istilah "nilai maksimum fungsi". Adalah mudah untuk melihat bahawa nilai maksimum hanya di kawasan kejiranan tempatan, dan di bahagian atas kiri terdapat "rakan seperjuangan yang lebih sejuk". Begitu juga, "minimum fungsi" tidak sama dengan "nilai minimum fungsi," dan dalam lukisan kita melihat bahawa nilai minimum hanya di kawasan tertentu. Dalam hal ini, titik ekstrem juga dipanggil titik ekstrem tempatan, dan yang melampau – ekstrem tempatan. Mereka berjalan dan merayau berhampiran dan global saudara. Jadi, mana-mana parabola mempunyai di puncaknya minimum global atau maksimum global. Selanjutnya, saya tidak akan membezakan antara jenis ekstrem, dan penjelasannya lebih banyak disuarakan untuk tujuan pendidikan umum - kata sifat tambahan "tempatan"/"global" seharusnya tidak mengejutkan anda.

Mari kita ringkaskan kami lawatan kecil ke dalam teori dengan pukulan ujian: apakah maksud tugas "mencari selang monotonicity dan titik ekstrem fungsi"?

Perkataan menggalakkan anda mencari:

– selang peningkatan/penurunan fungsi (tidak berkurang, tidak meningkat kelihatan lebih jarang);

– mata maksimum dan/atau minimum (jika ada). Nah, untuk mengelakkan kegagalan, lebih baik untuk mencari minimum/maksimum sendiri ;-)

Bagaimana untuk menentukan semua ini? Menggunakan fungsi terbitan!

Bagaimana untuk mencari selang peningkatan, penurunan,
titik ekstrem dan ekstrem fungsi?

Banyak peraturan, sebenarnya, sudah diketahui dan difahami dari pengajaran tentang maksud terbitan.

Terbitan tangen membawa berita gembira bahawa fungsi semakin meningkat sepanjang domain definisi.

Dengan kotangen dan terbitannya keadaannya adalah sebaliknya.

Arcsine meningkat sepanjang selang - terbitan di sini adalah positif: .
Apabila fungsi ditakrifkan, tetapi tidak boleh dibezakan. Walau bagaimanapun, pada titik kritikal terdapat terbitan tangan kanan dan tangen tangan kanan, dan di tepi yang satu lagi terdapat rakan kidal mereka.

Saya fikir ia tidak akan terlalu sukar untuk anda menjalankan penaakulan yang sama untuk kosinus arka dan terbitannya.

Semua kes di atas, kebanyakannya adalah derivatif jadual, saya ingatkan, ikuti terus dari definisi terbitan.

Mengapa meneroka fungsi menggunakan derivatifnya?

Untuk lebih memahami rupa graf fungsi ini: di mana ia pergi "bawah ke atas", di mana "atas ke bawah", di mana ia mencapai minimum dan maksimum (jika ia mencapai sama sekali). Tidak semua fungsi adalah begitu mudah - dalam kebanyakan kes kita tidak tahu sama sekali tentang graf fungsi tertentu.

Sudah tiba masanya untuk beralih kepada contoh yang lebih bermakna dan mempertimbangkan algoritma untuk mencari selang monotonicity dan extrema fungsi:

Contoh 1

Cari selang peningkatan/penurunan dan ekstrem fungsi

Penyelesaian:

1) Langkah pertama ialah mencari domain sesuatu fungsi, dan juga ambil perhatian tentang titik rehat (jika wujud). DALAM dalam kes ini fungsi itu berterusan pada keseluruhan garis nombor, dan tindakan ini pada tahap tertentu formal. Tetapi dalam beberapa kes, keghairahan yang serius berkobar di sini, jadi mari kita layan perenggan itu tanpa menghina.

2) Titik kedua algoritma adalah disebabkan oleh

syarat yang diperlukan untuk ekstrem:

Sekiranya terdapat ekstrem pada satu titik, maka sama ada nilai itu tidak wujud.

Bingung dengan pengakhirannya? Ekstrem bagi fungsi "modulus x". .

Syaratnya perlu, tetapi tidak cukup, dan sebaliknya tidak selalu benar. Jadi, ia belum lagi mengikuti dari kesamaan bahawa fungsi mencapai maksimum atau minimum pada titik . Contoh klasik sudah diserlahkan di atas - ini ialah parabola padu dan titik kritikalnya.

Tetapi walau bagaimanapun, syarat yang diperlukan untuk ekstrem menentukan keperluan untuk mencari perkara yang mencurigakan. Untuk melakukan ini, cari derivatif dan selesaikan persamaan:

Pada permulaan artikel pertama tentang graf fungsi Saya memberitahu anda cara membina parabola dengan cepat menggunakan contoh : “...kita ambil terbitan pertama dan samakannya dengan sifar: ...Jadi, penyelesaian kepada persamaan kita: - pada titik inilah puncak parabola itu terletak...”. Sekarang, saya fikir, semua orang memahami mengapa puncak parabola terletak tepat pada titik ini =) Secara umum, kita harus bermula dengan contoh yang sama di sini, tetapi ia terlalu mudah (walaupun untuk teko). Di samping itu, terdapat analog pada akhir pelajaran tentang terbitan bagi suatu fungsi. Oleh itu, mari kita tingkatkan ijazah:

Contoh 2

Cari selang kemonotonan dan keterlaluan fungsi

Ini adalah contoh untuk keputusan bebas. Penyelesaian lengkap dan anggaran sampel akhir tugasan pada akhir pelajaran.

Saat yang ditunggu-tunggu untuk bertemu dengan fungsi pecahan-rasional telah tiba:

Contoh 3

Teroka fungsi menggunakan terbitan pertama

Beri perhatian kepada bagaimana kepelbagaian satu dan tugas yang sama boleh dirumuskan semula.

Penyelesaian:

1) Fungsi mengalami ketakselanjaran tak terhingga pada titik.

2) Kami mengesan titik kritikal. Mari cari derivatif pertama dan samakannya dengan sifar:

Mari kita selesaikan persamaan. Pecahan adalah sifar apabila pengangkanya adalah sifar:

Oleh itu, kami mendapat tiga mata kritikal:

3) Kami memplot SEMUA titik yang dikesan pada garis nombor dan kaedah selang waktu kami mentakrifkan tanda-tanda DERIVATIF:

Saya mengingatkan anda bahawa anda perlu mengambil beberapa titik dalam selang dan mengira nilai derivatif padanya dan tentukan tandanya. Lebih menguntungkan untuk tidak mengira, tetapi untuk "menganggarkan" secara lisan. Mari kita ambil, sebagai contoh, titik kepunyaan selang dan lakukan penggantian: .

Dua "tambah" dan satu "tolak" memberikan "tolak", oleh itu, yang bermaksud bahawa terbitan adalah negatif sepanjang keseluruhan selang.

Tindakan itu, seperti yang anda faham, perlu dijalankan untuk setiap enam selang. Ngomong-ngomong, ambil perhatian bahawa faktor pengangka dan penyebut adalah positif untuk sebarang titik dalam mana-mana selang, yang sangat memudahkan tugas.

Jadi, derivatif memberitahu kami bahawa FUNGSI SENDIRI meningkat sebanyak dan berkurangan sebanyak . Ia adalah mudah untuk menyambungkan selang jenis yang sama dengan ikon gabungan.

Pada ketika fungsi mencapai maksimum:
Pada titik fungsi mencapai minimum:

Fikirkan mengapa anda tidak perlu mengira semula nilai kedua ;-)

Apabila melalui titik, terbitan tidak menukar tanda, jadi fungsi TIADA EXTREMUM di sana - kedua-duanya menurun dan kekal menurun.

! Jom ulang perkara penting : mata tidak dianggap kritikal - ia mengandungi fungsi tidak ditentukan. Sehubungan itu, di sini Pada dasarnya tidak boleh ada keterlaluan(walaupun derivatif bertukar tanda).

Jawab: fungsi meningkat sebanyak dan berkurang sebanyak Pada titik maksimum fungsi dicapai: , dan pada titik – minimum: .

Pengetahuan tentang selang monotonicity dan extrema, ditambah dengan yang telah ditetapkan asimtot sudah memberikan idea yang sangat baik tentang penampilan grafik fungsi. Seseorang yang mempunyai latihan sederhana dapat menentukan secara lisan bahawa graf fungsi mempunyai dua asimtot menegak dan asimtot serong. Inilah wira kami:

Cuba sekali lagi untuk mengaitkan hasil kajian dengan graf fungsi ini.
Tidak ada ekstrem pada titik kritikal, tetapi ada infleksi graf(yang, sebagai peraturan, berlaku dalam kes yang serupa).

Contoh 4

Cari ekstrem bagi fungsi tersebut

Contoh 5

Cari selang monotonicity, maksima dan minima bagi fungsi tersebut

…ia hampir seperti percutian "X dalam kiub" hari ini....
Soooo, siapa di galeri yang menawarkan untuk minum untuk ini? =)

Setiap tugas mempunyai nuansa substantif dan kehalusan teknikalnya sendiri, yang diulas pada akhir pelajaran.

Pertimbangkan graf bagi fungsi selanjar y=f(x) ditunjukkan dalam rajah.

Nilai fungsi pada satu titik x 1 akan lebih besar daripada nilai fungsi di semua titik jiran di sebelah kiri dan di sebelah kanan x 1 . Dalam kes ini kita mengatakan bahawa fungsi mempunyai pada titik x 1 maksimum. Pada titik itu x Fungsi 3 jelas juga mempunyai maksimum. Jika kita mempertimbangkan perkara itu x 2, maka nilai fungsi di dalamnya adalah kurang daripada semua nilai jiran. Dalam kes ini kita mengatakan bahawa fungsi mempunyai pada titik x 2 minimum. Begitu juga untuk perkara itu x 4 .

Fungsi y=f(x) pada titik x 0 telah maksimum, jika nilai fungsi pada titik ini lebih besar daripada nilainya pada semua titik selang tertentu yang mengandungi titik x 0, iaitu jika terdapat kejiranan seperti itu x 0, yang untuk semua orang x≠x 0 , kepunyaan kejiranan ini, ketidaksamaan berlaku f(x)<f(x 0 ) .

Fungsi y=f(x) Ia ada minimum pada titik x 0 , jika terdapat kejiranan seperti itu x 0 , itu untuk semua orang x≠x 0 kepunyaan kejiranan ini, ketidaksamaan berlaku f(x)>f(x 0.

Titik di mana fungsi mencapai maksimum dan minimum dipanggil titik ekstrem, dan nilai fungsi pada titik ini dipanggil ekstrem fungsi.

Mari kita perhatikan fakta bahawa fungsi yang ditakrifkan pada segmen boleh mencapai maksimum dan minimumnya hanya pada titik yang terkandung dalam segmen yang sedang dipertimbangkan.

Ambil perhatian bahawa jika fungsi mempunyai maksimum pada satu titik, ini tidak bermakna bahawa pada ketika itu fungsi mempunyai nilai terbesar dalam keseluruhan domain definisi. Dalam rajah yang dibincangkan di atas, fungsi pada titik x 1 mempunyai maksimum, walaupun terdapat titik di mana nilai fungsi lebih besar daripada pada titik x 1 . khususnya, f(x 1) < f(x 4) iaitu minimum sesuatu fungsi adalah lebih besar daripada maksimum. Daripada takrifan maksimum ia hanya mengikuti bahawa ini adalah yang paling sangat penting berfungsi pada titik yang cukup dekat dengan titik maksimum.

Teorem 1. (Syarat yang diperlukan untuk kewujudan ekstrem.) Jika fungsi boleh beza y=f(x) mempunyai pada titik x=x 0 extremum, maka terbitannya pada ketika ini menjadi sifar.

Bukti. Biarkan, untuk kepastian, pada titik itu x 0 mempunyai fungsi maksimum. Kemudian, untuk kenaikan yang cukup kecil Δ x kita ada f(x 0 + Δ x) 0 ) , iaitu Tetapi kemudian

Melepasi ketaksamaan ini kepada had pada Δ x→ 0 dan mengambil kira bahawa terbitan f "(x 0) wujud, dan oleh itu had di sebelah kiri tidak bergantung pada bagaimana Δ x→ 0, kita dapat: pada Δ x → 0 – 0 f"(x 0) ≥ 0 a pada Δ x → 0 + 0 f"(x 0) ≤ 0. Sejak f"(x 0) mentakrifkan nombor, maka kedua-dua ketaksamaan ini hanya serasi jika f"(x 0) = 0.

Teorem terbukti menyatakan bahawa titik maksimum dan minimum hanya boleh berada di antara nilai-nilai hujah di mana terbitan menjadi sifar.

Kami mempertimbangkan kes apabila fungsi mempunyai derivatif di semua titik segmen tertentu. Apakah keadaan dalam kes di mana derivatif tidak wujud? Mari lihat contoh.

Contoh.

1. y=|x|.

   Fungsi tersebut tidak mempunyai derivatif pada titik tersebut x=0 (pada ketika ini graf fungsi tidak mempunyai tangen yang ditentukan), tetapi pada ketika ini fungsi mempunyai minimum, kerana y(0)=0, dan untuk semua x≠ 0y > 0.



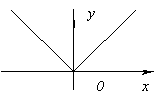
Fungsi ini tidak mempunyai derivatif pada x=0, kerana ia pergi ke infiniti di x=0. Tetapi pada ketika ini fungsi mempunyai maksimum.



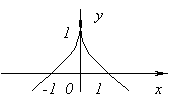
Fungsi ini tidak mempunyai derivatif pada x=0, sejak di x→0. Pada ketika ini fungsi tidak mempunyai maksimum atau minimum. sungguh, f(x)=0 dan pada x<0f(x)<0, а при x>0f(x)>0.



Oleh itu, daripada contoh yang diberikan dan teorem yang dirumuskan, adalah jelas bahawa fungsi boleh mempunyai ekstrem hanya dalam dua kes: 1) pada titik di mana terbitan wujud dan sama dengan sifar; 2) pada titik di mana derivatif tidak wujud.

Namun, jika pada satu ketika x 0 kita tahu itu f "(x 0 ) =0, maka seseorang tidak boleh membuat kesimpulan daripada ini bahawa pada titik itu x 0 fungsi mempunyai ekstrem.

Sebagai contoh. .



Tetapi tempoh x=0 bukan titik ekstrem, kerana di sebelah kiri titik ini nilai fungsi terletak di bawah paksi lembu, dan di sebelah kanan di atas.

Nilai hujah daripada domain fungsi di mana terbitan fungsi hilang atau tidak wujud dipanggil titik kritikal.




Daripada semua perkara di atas, ia menunjukkan bahawa titik ekstrem fungsi adalah antara titik kritikal, dan, bagaimanapun, tidak setiap titik kritikal adalah titik ekstrem. Oleh itu, untuk mencari ekstrem fungsi, anda perlu mencari semua titik kritikal fungsi, dan kemudian memeriksa setiap titik ini secara berasingan untuk maksimum dan minimum. Teorem berikut berfungsi untuk tujuan ini.

Teorem 2. (Syarat yang mencukupi untuk kewujudan ekstrem.) Biarkan fungsi itu berterusan pada beberapa selang yang mengandungi titik kritikal x 0, dan boleh dibezakan pada semua titik selang ini (kecuali, mungkin, titik itu sendiri x 0). Jika, apabila bergerak dari kiri ke kanan melalui titik ini, derivatif berubah tanda dari tambah kepada tolak, maka pada titik x = x 0 mempunyai fungsi maksimum. Jika, apabila melalui x 0 dari kiri ke kanan, derivatif bertukar tanda dari tolak ke tambah, maka fungsi mempunyai minimum pada ketika ini.

Justeru, jika

Bukti. Mari kita anggap bahawa apabila melalui x 0 tanda perubahan terbitan daripada tambah kepada tolak, i.e. di hadapan semua orang x, dekat dengan tujuan x 0 f "(x)> 0 untuk x< x 0 , f "(x)< 0 untuk x>x 0 . Mari gunakan teorem Lagrange kepada perbezaan f(x) - f(x 0 ) = f "(c)(x- x 0), di mana c terletak di antara x Dan x 0 .

1. biarlah x< x 0 . Kemudian c< x 0 dan f "(c)> 0. sebab tu f "(c)(x- x 0)< 0 dan oleh itu

   f(x) - f(x 0 )< 0, iaitu f(x)< f(x 0 ).

2. biarlah x > x 0 . Kemudian c>x 0 dan f "(c)< 0. Bermakna f "(c)(x- x 0)< 0. sebab tu f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Oleh itu, untuk semua nilai x cukup dekat dengan x 0 f(x)< f(x 0 ) . Dan ini bermakna bahawa pada titik itu x 0 mempunyai fungsi maksimum.

Bahagian kedua teorem minimum dibuktikan dengan cara yang sama.



Mari kita jelaskan maksud teorem ini dalam rajah. biarlah f "(x 1 ) =0 dan untuk mana-mana x, cukup dekat dengan x 1, ketidaksamaan dipenuhi

f "(x)< 0 pada x< x 1 , f "(x)> 0 pada x>x 1 .

Kemudian ke kiri titik x 1 fungsi bertambah dan berkurang di sebelah kanan, oleh itu, apabila x = x 1 fungsi pergi daripada meningkat kepada menurun, iaitu, ia mempunyai maksimum.

Begitu juga, kita boleh mempertimbangkan mata x 2 dan x 3 .


Semua perkara di atas boleh digambarkan secara skematik dalam gambar:

Peraturan untuk mengkaji fungsi y=f(x) untuk ekstrem

1. Cari domain bagi suatu fungsi f(x).
2. Cari terbitan pertama bagi suatu fungsi f "(x).
3. Tentukan titik kritikal untuk ini:
   1. cari punca sebenar persamaan f "(x)=0;
   2. cari semua nilai x yang mana derivatifnya f "(x) tidak wujud.
4. Tentukan tanda terbitan di sebelah kiri dan kanan titik genting. Oleh kerana tanda terbitan kekal malar antara dua titik genting, adalah memadai untuk menentukan tanda terbitan pada satu titik ke kiri dan satu titik di sebelah kanan titik genting.
5. Kira nilai fungsi pada titik ekstrem.

Contoh. Teroka fungsi untuk minimum dan maksimum.




NILAI MAKSIMUM DAN TERKECIL FUNGSI PADA Segmen

Terbesar nilai fungsi pada selang adalah yang terbesar daripada semua nilainya pada selang ini, dan yang paling kecil– yang terkecil daripada semua nilainya.

Pertimbangkan fungsinya y=f(x) berterusan pada segmen [ a, b]. Seperti yang diketahui, fungsi sedemikian mencapai nilai maksimum dan minimumnya, sama ada di sempadan segmen atau di dalamnya. Jika nilai terbesar atau terkecil fungsi dicapai pada titik dalaman segmen, maka nilai ini adalah maksimum atau minimum fungsi, iaitu, ia dicapai pada titik kritikal.

Oleh itu, kami mendapat yang berikut peraturan untuk mencari nilai terbesar dan terkecil fungsi pada segmen[ a, b] :

1. Cari semua titik genting bagi fungsi dalam selang ( a, b) dan hitung nilai fungsi pada titik ini.
2. Kira nilai fungsi pada hujung segmen apabila x = a, x = b.
3. Daripada semua nilai yang diperoleh, pilih yang terbesar dan terkecil.