Fungsi penukaran graf dan graf. Transformasi graf fungsi asas

Pemindahan selari.

TERJEMAHAN SEPANJANG Y-AXIS

f(x) => f(x) - b
Katakan anda ingin membina graf bagi fungsi y = f(x) - b. Adalah mudah untuk melihat bahawa ordinat graf ini untuk semua nilai x pada |b| unit kurang daripada koordinat sepadan graf fungsi y = f(x) untuk b>0 dan |b| unit lebih - pada b 0 atau ke atas pada b Untuk memplot graf bagi fungsi y + b = f(x), anda hendaklah membina graf bagi fungsi y = f(x) dan gerakkan paksi-x ke |b| unit naik pada b>0 atau oleh |b| unit turun pada b

PINDAHKAN SEPANJANG PAKSI ABSCISS

f(x) => f(x + a)
Katakan anda ingin memplot fungsi y = f(x + a). Pertimbangkan fungsi y = f(x), yang pada satu titik x = x1 mengambil nilai y1 = f(x1). Jelas sekali, fungsi y = f(x + a) akan mengambil nilai yang sama pada titik x2, koordinatnya ditentukan daripada kesamaan x2 + a = x1, i.e. x2 = x1 - a, dan kesamaan yang sedang dipertimbangkan adalah sah untuk keseluruhan semua nilai dari domain takrifan fungsi. Oleh itu, graf fungsi y = f(x + a) boleh diperolehi secara selari dengan menggerakkan graf fungsi y = f(x) di sepanjang paksi-x ke kiri dengan |a| unit untuk a > 0 atau ke kanan oleh |a| unit untuk a Untuk membina graf bagi fungsi y = f(x + a), anda hendaklah membina graf bagi fungsi y = f(x) dan gerakkan paksi ordinat ke |a| unit ke kanan apabila a>0 atau oleh |a| unit ke kiri di a

Contoh:

1.y=f(x+a)

2.y=f(x)+b

Refleksi.

PEMBINAAN GRAF FUNGSI BENTUK Y = F(-X)

f(x) => f(-x)
Jelaslah bahawa fungsi y = f(-x) dan y = f(x) mengambil nilai yang sama pada titik yang abscissasnya sama dalam nilai mutlak tetapi bertentangan dalam tanda. Dalam erti kata lain, ordinat graf fungsi y = f(-x) dalam kawasan nilai positif (negatif) x akan sama dengan ordinat graf fungsi y = f(x) untuk nilai negatif (positif) yang sepadan bagi x dalam nilai mutlak. Oleh itu, kita mendapat peraturan berikut.
Untuk memplot fungsi y = f(-x), anda hendaklah memplot fungsi y = f(x) dan mencerminkannya secara relatif kepada ordinat. Graf yang terhasil ialah graf bagi fungsi y = f(-x)

PEMBINAAN GRAF FUNGSI BENTUK Y = - F(X)

f(x) => - f(x)
Ordinasi graf fungsi y = - f(x) untuk semua nilai argumen adalah sama dalam nilai mutlak, tetapi bertentangan dalam tanda dengan ordinat graf fungsi y = f(x) untuk nilai hujah yang sama. Oleh itu, kita mendapat peraturan berikut.
Untuk memplot graf bagi fungsi y = - f(x), anda hendaklah memplot graf bagi fungsi y = f(x) dan mencerminkannya secara relatif kepada paksi-x.

Contoh:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Ubah bentuk.

DEFORMASI GRAF SEPANJANG PAksi Y

f(x) => k f(x)
Pertimbangkan fungsi dalam bentuk y = k f(x), dengan k > 0. Adalah mudah untuk melihat bahawa dengan nilai hujah yang sama, ordinat graf fungsi ini akan menjadi k kali lebih besar daripada ordinat bagi graf bagi fungsi y = f(x) untuk k > 1 atau 1/k kali kurang daripada ordinat graf bagi fungsi y = f(x) untuk k Untuk membina graf bagi fungsi y = k f(x) ), anda hendaklah membina graf bagi fungsi y = f(x) dan menambah ordinatnya sebanyak k kali untuk k > 1 (regangkan graf sepanjang paksi ordinat ) atau kurangkan ordinatnya sebanyak 1/k kali pada k
k > 1- regangan dari paksi Lembu
0 - mampatan ke paksi OX

DEFORMASI GRAF SEPANJANG PAKSI ABSCISS

f(x) => f(k x)
Biarkan perlu untuk membina graf bagi fungsi y = f(kx), dengan k>0. Pertimbangkan fungsi y = f(x), yang pada titik arbitrari x = x1 mengambil nilai y1 = f(x1). Adalah jelas bahawa fungsi y = f(kx) mengambil nilai yang sama pada titik x = x2, koordinatnya ditentukan oleh kesamaan x1 = kx2, dan kesamaan ini sah untuk keseluruhan semua nilai x daripada domain takrifan fungsi. Akibatnya, graf fungsi y = f(kx) ternyata dimampatkan (untuk k 1) di sepanjang paksi absis berbanding dengan graf fungsi y = f(x). Oleh itu, kita mendapat peraturan.
Untuk membina graf bagi fungsi y = f(kx), anda hendaklah membina graf bagi fungsi y = f(x) dan mengurangkan absisnya sebanyak k kali untuk k>1 (mampatkan graf sepanjang paksi absis) atau tambah abscissasnya sebanyak 1/k kali ganda untuk k
k > 1- mampatan ke paksi Oy
0 - regangan dari paksi OY

Kerja itu dijalankan oleh Alexander Chichkanov, Dmitry Leonov di bawah bimbingan T.V. Tkach, S.M. Vyazov, I.V. Ostroverkhova.
©2014

Teks kerja disiarkan tanpa imej dan formula.
Versi penuh kerja tersedia dalam tab "Fail Kerja" dalam format PDF

pengenalan

Mengubah graf fungsi adalah salah satu konsep asas matematik yang berkaitan secara langsung dengan aktiviti amali. Transformasi graf fungsi pertama kali ditemui dalam algebra gred 9 apabila mempelajari topik "Fungsi Kuadratik". Fungsi kuadratik diperkenalkan dan dikaji berhubung rapat dengan persamaan kuadratik dan ketidaksamaan. Banyak konsep matematik turut dibincangkan kaedah grafik, sebagai contoh, dalam gred 10-11, kajian fungsi memungkinkan untuk mencari domain definisi dan domain nilai fungsi, domain menurun atau meningkat, asimtot, selang tanda malar, dll. Ini penting. isu juga dibangkitkan di GIA. Ia berikutan bahawa membina dan mengubah graf fungsi adalah salah satu tugas utama mengajar matematik di sekolah.

Walau bagaimanapun, untuk memplot graf bagi banyak fungsi, anda boleh menggunakan beberapa kaedah yang memudahkan perancangan. Perkara di atas menentukan perkaitan topik kajian.

Objek kajian adalah untuk mengkaji transformasi graf dalam matematik sekolah.

Subjek kajian - proses membina dan mengubah graf fungsi di sekolah menengah.

Soalan bermasalah: Adakah mungkin untuk membina graf bagi fungsi yang tidak dikenali jika anda mempunyai kemahiran menukar graf? fungsi asas?

Sasaran: memplot fungsi dalam situasi yang tidak biasa.

Tugasan:

1. Menganalisis bahan pendidikan tentang masalah yang dikaji. 2. Mengenal pasti skema untuk mengubah graf fungsi dalam kursus matematik sekolah. 3. Pilih yang paling banyak kaedah yang berkesan dan alatan untuk membina dan mengubah graf fungsi. 4. Dapat mengaplikasikan teori ini dalam menyelesaikan masalah.

Pengetahuan awal, kemahiran dan kebolehan yang diperlukan:

Tentukan nilai fungsi dengan nilai hujahnya apabila dalam pelbagai cara tugasan fungsi;

Bina graf bagi fungsi yang dikaji;

Huraikan kelakuan dan sifat fungsi menggunakan graf dan, dalam kes termudah, menggunakan formula; cari nilai terbesar dan terkecil daripada graf fungsi;

Penerangan menggunakan fungsi pelbagai kebergantungan, mewakilinya secara grafik, mentafsir graf.

Bahagian utama

Bahagian teori

Sebagai graf awal bagi fungsi y = f(x), saya akan memilih fungsi kuadratik y = x 2 . Saya akan mempertimbangkan kes-kes transformasi graf ini yang dikaitkan dengan perubahan dalam formula yang mentakrifkan fungsi ini dan membuat kesimpulan untuk sebarang fungsi.

1. Fungsi y = f(x) + a

Dalam formula baharu, nilai fungsi (ordinat titik graf) berubah mengikut nombor a, berbanding dengan nilai fungsi "lama". Ini membawa kepada pemindahan selari graf fungsi sepanjang paksi OY:

naik jika a > 0; turun jika a< 0.

KESIMPULAN

Oleh itu, graf fungsi y=f(x)+a diperoleh daripada graf fungsi y=f(x) menggunakan terjemahan selari di sepanjang paksi ordinat oleh unit ke atas jika a > 0, dan oleh unit ke bawah sekiranya< 0.

2. Fungsi y = f(x-a),

Dalam formula baharu, nilai argumen (abscissas titik graf) berubah mengikut nombor a, berbanding dengan nilai argumen "lama". Ini membawa kepada pemindahan selari graf fungsi sepanjang paksi OX: ke kanan, jika a< 0, влево, если a >0.

KESIMPULAN

Ini bermakna graf fungsi y= f(x - a) diperoleh daripada graf fungsi y=f(x) melalui terjemahan selari di sepanjang paksi absis oleh unit ke kiri jika a > 0, dan dengan a unit ke kanan jika a< 0.

3. Fungsi y = k f(x), dengan k > 0 dan k ≠ 1

Dalam formula baharu, nilai fungsi (ordinat titik graf) berubah k kali berbanding dengan nilai fungsi "lama". Ini membawa kepada: 1) "regangan" dari titik (0; 0) di sepanjang paksi OY dengan faktor k, jika k > 1, 2) "mampatan" ke titik (0; 0) di sepanjang paksi OY dengan faktor, jika 0< k < 1.

KESIMPULAN

Akibatnya: untuk membina graf bagi fungsi y = kf(x), di mana k > 0 dan k ≠ 1, anda perlu mendarabkan ordinat bagi titik graf bagi fungsi y = f(x) yang diberikan dengan k. Penjelmaan sedemikian dipanggil regangan dari titik (0; 0) sepanjang paksi OY k kali jika k > 1; mampatan ke titik (0; 0) sepanjang masa paksi OY jika 0< k < 1.

4. Fungsi y = f(kx), dengan k > 0 dan k ≠ 1

Dalam formula baharu, nilai argumen (abscissas titik graf) berubah k kali berbanding dengan nilai argumen "lama". Ini membawa kepada: 1) "regangan" dari titik (0; 0) di sepanjang paksi OX sebanyak 1/k kali, jika 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

KESIMPULAN

Jadi: untuk membina graf fungsi y = f(kx), di mana k > 0 dan k ≠ 1, anda perlu mendarabkan absis titik-titik graf fungsi y=f(x) yang diberikan dengan k . Penjelmaan sedemikian dipanggil regangan dari titik (0; 0) di sepanjang paksi OX sebanyak 1/k kali, jika 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. Fungsi y = - f (x).

Dalam formula ini, nilai fungsi (ordinat titik graf) diterbalikkan. Perubahan ini membawa kepada paparan simetri graf asal fungsi berbanding paksi Lembu.

KESIMPULAN

Untuk memplot graf bagi fungsi y = - f (x), anda memerlukan graf bagi fungsi y= f(x)

mencerminkan secara simetri tentang paksi OX. Penjelmaan ini dipanggil penjelmaan simetri tentang paksi OX.

6. Fungsi y = f (-x).

Dalam formula ini, nilai hujah (abscissa titik graf) diterbalikkan. Perubahan ini membawa kepada paparan simetri graf asal fungsi berbanding paksi OY.

Contoh untuk fungsi y = - x² penjelmaan ini tidak ketara, kerana fungsi ini genap dan graf tidak berubah selepas penjelmaan. Penjelmaan ini boleh dilihat apabila fungsi itu ganjil dan apabila ia bukan genap atau ganjil.

7. Fungsi y = |f(x)|.

Dalam formula baharu, nilai fungsi (ordinat titik graf) berada di bawah tanda modulus. Ini membawa kepada kehilangan bahagian graf fungsi asal dengan ordinat negatif (iaitu, bahagian yang terletak di separuh satah bawah berbanding paksi Lembu) dan paparan simetri bahagian ini berbanding paksi Lembu.

8. Fungsi y= f (|x|).

Dalam formula baharu, nilai hujah (abscissas titik graf) berada di bawah tanda modulus. Ini membawa kepada kehilangan bahagian graf fungsi asal dengan absis negatif (iaitu, terletak di separuh satah kiri berbanding paksi OY) dan penggantiannya dengan bahagian graf asal yang simetri berbanding paksi OY .

Bahagian praktikal

Mari kita lihat beberapa contoh aplikasi teori di atas.

CONTOH 1.

Penyelesaian. Jom tukar formula ini:

1) Mari bina graf fungsi

CONTOH 2.

Graf fungsi yang diberikan oleh formula

Penyelesaian. Mari kita ubah formula ini dengan menyerlahkan dalam ini trinomial kuadratik kuasa dua binomial:

1) Mari bina graf fungsi

2) Lakukan pemindahan selari graf yang dibina kepada vektor

CONTOH 3.

TUGASAN DARI Peperiksaan Negeri Bersatu Mengraf Fungsi Piecewise

Graf fungsi Graf fungsi y=|2(x-3)2-2|; 1

Fungsi asas asas dalam bentuk tulennya tanpa transformasi jarang berlaku, jadi selalunya anda perlu bekerja dengan fungsi asas yang diperoleh daripada yang utama dengan menambah pemalar dan pekali. Graf sedemikian dibina menggunakan transformasi geometri bagi fungsi asas yang diberikan.

Mari kita lihat contoh fungsi kuadratik daripada bentuk y = - 1 3 x + 2 3 2 + 2, grafnya ialah parabola y = x 2, yang dimampatkan tiga kali relatif kepada O y dan relatif simetri kepada O x, dan dianjak oleh 2 3 sepanjang O x ke kanan, sebanyak 2 unit sepanjang O u ke atas. Pada garis koordinat ia kelihatan seperti ini:

Yandex.RTB R-A-339285-1

Penjelmaan geometri bagi graf fungsi

Menggunakan penjelmaan geometri graf yang diberikan, kita memperoleh bahawa graf itu digambarkan oleh fungsi bentuk ± k 1 · f (± k 2 · (x + a)) + b, apabila k 1 > 0, k 2 > 0 adalah pekali mampatan pada 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 sepanjang O y dan O x. Tanda di hadapan pekali k 1 dan k 2 menunjukkan paparan simetri graf berbanding paksi, a dan b menganjaknya sepanjang O x dan sepanjang O y.

Definisi 1

Ada 3 jenis transformasi geometri graf:

• Penskalaan sepanjang O x dan O y. Ini dipengaruhi oleh pekali k 1 dan k 2 dengan syarat ia tidak sama dengan 1 apabila 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, maka graf diregangkan di sepanjang O y dan dimampatkan di sepanjang O x.
• Paparan simetri relatif kepada paksi koordinat. Jika terdapat tanda “-” di hadapan k 1, simetri adalah relatif kepada O x, dan di hadapan k 2 ia adalah relatif kepada O y. Jika "-" tiada, maka item itu dilangkau semasa menyelesaikan;
• Pemindahan selari (anjakan) sepanjang O x dan O y. Penjelmaan dilakukan jika terdapat pekali a dan b tidak sama dengan 0. Jika a positif, graf dianjak ke kiri oleh | a | unit, jika a adalah negatif, maka ke kanan pada jarak yang sama. Nilai b menentukan pergerakan sepanjang paksi O y, yang bermaksud apabila b positif, fungsi bergerak ke atas, dan apabila b negatif, ia bergerak ke bawah.

Mari kita lihat penyelesaian menggunakan contoh, bermula dengan fungsi kuasa.

Contoh 1

Ubah y = x 2 3 dan plotkan fungsi y = - 1 2 · 8 x - 4 2 3 + 3 .

Penyelesaian

Mari kita wakili fungsi dengan cara ini:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Di mana k 1 = 2, adalah bernilai memberi perhatian kepada kehadiran "-", a = - 1 2, b = 3. Dari sini kita dapati bahawa penjelmaan geometri dilakukan dengan meregangkan sepanjang O y dua kali, dipaparkan secara simetri berbanding O x, beralih ke kanan sebanyak 1 2 dan ke atas sebanyak 3 unit.

Jika kita menggambarkan fungsi kuasa asal, kita mendapatnya

apabila diregangkan dua kali sepanjang O y kita mempunyai itu

Pemetaan, simetri berkenaan dengan O x, mempunyai bentuk

dan bergerak ke kanan sebanyak 1 2

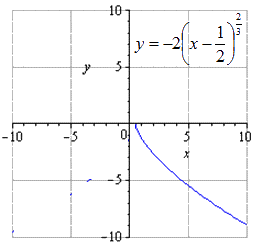
pergerakan 3 unit ke atas kelihatan seperti

Mari kita lihat transformasi fungsi eksponen menggunakan contoh.

Contoh 2

Bina graf bagi fungsi eksponen y = - 1 2 1 2 (2 - x) + 8.

Penyelesaian.

Mari kita ubah fungsi berdasarkan sifat fungsi kuasa. Kemudian kita dapat itu

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Daripada ini kita dapat melihat bahawa kita mendapat rantaian transformasi y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Kami mendapati bahawa yang asli fungsi eksponen kelihatan seperti

Memerah dua kali sepanjang O y memberi

Regangan sepanjang O x

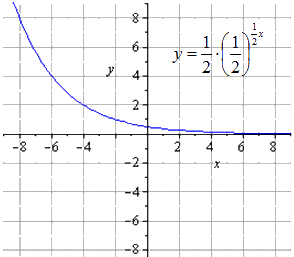
Pemetaan simetri berkenaan dengan O x

Pemetaan adalah simetri berkenaan dengan O y

Naik 8 unit

Mari kita lihat penyelesaian menggunakan contoh fungsi logaritma y = log(x) .

Contoh 3

Bina fungsi y = ln e 2 · - 1 2 x 3 menggunakan penjelmaan y = ln (x) .

Penyelesaian

Untuk menyelesaikannya perlu menggunakan sifat-sifat logaritma, maka kita dapat:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Penjelmaan fungsi logaritma kelihatan seperti ini:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Mari kita plot fungsi logaritma asal

Kami memampatkan sistem mengikut O y

Kami meregangkan sepanjang O x

Kami melakukan pemetaan berkenaan dengan O y

Kami beralih kepada 2 unit, kami dapat

Untuk menukar graf fungsi trigonometri adalah perlu untuk memuatkan skema penyelesaian dalam bentuk ± k 1 · f (± k 2 · (x + a)) + b. Adalah perlu bahawa k 2 sama dengan T k 2 . Dari sini kita dapat 0 itu< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Mari kita lihat contoh penyelesaian masalah dengan penjelmaan y = sin x.

Contoh 4

Bina graf y = - 3 sin 1 2 x - 3 2 - 2 menggunakan penjelmaan fungsi y=sinx.

Penyelesaian

Ia adalah perlu untuk mengurangkan fungsi kepada bentuk ± k 1 · f ± k 2 · x + a + b. Untuk ini:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Dapat dilihat bahawa k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Oleh kerana terdapat "-" sebelum k 1, tetapi tidak sebelum k 2, maka kita mendapat rantaian transformasi bentuk:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Transformasi gelombang sinus terperinci. Apabila memplot sinusoid asal y = sin (x), kita dapati bahawa tempoh positif terkecil dianggap sebagai T = 2 π. Mencari maksimum pada titik π 2 + 2 π · k; 1, dan minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

O y diregangkan tiga kali ganda, yang bermaksud peningkatan amplitud ayunan akan meningkat sebanyak 3 kali ganda. T = 2 π ialah tempoh positif terkecil. Maksimum pergi ke π 2 + 2 π · k; 3, k ∈ Z, minima - - π 2 + 2 π · k; - 3, k ∈ Z.

Apabila meregangkan sepanjang O x sebanyak separuh, kita dapati bahawa tempoh positif terkecil meningkat sebanyak 2 kali ganda dan bersamaan dengan T = 2 π k 2 = 4 π. Maksimum pergi ke π + 4 π · k; 3, k ∈ Z, minimum – dalam - π + 4 π · k; - 3, k ∈ Z.

Imej dihasilkan secara simetri berkenaan dengan O x. Tempoh positif terkecil dalam kes ini tidak berubah dan sama dengan T = 2 π k 2 = 4 π. Peralihan maksimum kelihatan seperti - π + 4 π · k; 3, k ∈ Z, dan minimum ialah π + 4 π · k; - 3, k ∈ Z.

Graf dianjak ke bawah sebanyak 2 unit. Tempoh biasa minimum tidak berubah. Mencari maksima dengan peralihan kepada titik - π + 3 + 4 π · k; 1, k ∈ Z, minimum - π + 3 + 4 π · k; - 5 , k ∈ Z .

hidup di fasa ini graf bagi fungsi trigonometri dianggap berubah.

Mari kita pertimbangkan penjelmaan terperinci bagi fungsi y = cos x.

Contoh 5

Bina graf bagi fungsi y = 3 2 cos 2 - 2 x + 1 menggunakan penjelmaan fungsi dalam bentuk y = cos x.

Penyelesaian

Mengikut algoritma, adalah perlu untuk mengurangkan fungsi yang diberikan kepada bentuk ± k 1 · f ± k 2 · x + a + b. Kemudian kita dapat itu

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Daripada keadaan itu jelas bahawa k 1 = 3 2, k 2 = 2, a = - 1, b = 1, di mana k 2 mempunyai "-", tetapi sebelum k 1 ia tidak hadir.

Daripada ini kita melihat bahawa kita mendapat graf fungsi trigonometri dalam bentuk:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1

Transformasi kosinus langkah demi langkah dengan ilustrasi grafik.

Memandangkan graf y = cos(x), adalah jelas bahawa jumlah tempoh terpendek ialah T = 2π. Mencari maksima dalam 2 π · k ; 1, k ∈ Z, dan terdapat π + 2 π · k minima; - 1, k ∈ Z.

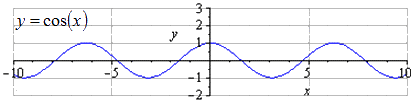
Apabila diregangkan sepanjang Oy sebanyak 3 2 kali, amplitud ayunan bertambah sebanyak 3 2 kali. T = 2 π ialah tempoh positif terkecil. Mencari maksima dalam 2 π · k ; 3 2, k ∈ Z, minima dalam π + 2 π · k; - 3 2 , k ∈ Z .

Apabila dimampatkan sepanjang O x separuh, kita dapati bahawa tempoh positif terkecil ialah nombor T = 2 π k 2 = π. Peralihan maksima kepada π · k berlaku; 3 2 , k ∈ Z , minimum - π 2 + π · k ; - 3 2 , k ∈ Z .

Pemetaan simetri berkenaan dengan Oy. Oleh kerana graf adalah ganjil, ia tidak akan berubah.

Apabila graf dianjak sebanyak 1 . Tiada perubahan dalam tempoh positif terkecil T = π. Mencari maksima dalam π · k + 1 ; 3 2, k ∈ Z, minimum - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Apabila dianjak sebanyak 1, tempoh positif terkecil adalah sama dengan T = π dan tidak diubah. Mencari maksima dalam π · k + 1 ; 5 2, k ∈ Z, minima dalam π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Penjelmaan fungsi kosinus selesai.

Mari kita pertimbangkan penjelmaan menggunakan contoh y = t g x.

Contoh 6

Bina graf bagi fungsi y = - 1 2 t g π 3 - 2 3 x + π 3 menggunakan penjelmaan fungsi y = t g (x) .

Penyelesaian

Sebagai permulaan, adalah perlu untuk mengurangkan fungsi yang diberikan kepada bentuk ± k 1 · f ± k 2 · x + a + b, selepas itu kita memperolehnya

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Jelas kelihatan bahawa k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, dan di hadapan pekali k 1 dan k 2 terdapat "-". Ini bermakna selepas mengubah tangentsoid yang kita dapat

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Transformasi langkah demi langkah bagi tangen dengan perwakilan grafik.

Kami mempunyai bahawa graf asal ialah y = t g (x) . Perubahan dalam tempoh positif adalah sama dengan T = π. Domain definisi dianggap sebagai - π 2 + π · k ; π 2 + π · k, k ∈ Z.

Kami memampatkannya 2 kali sepanjang Oy. T = π dianggap sebagai tempoh positif terkecil, di mana domain definisi mempunyai bentuk - π 2 + π · k; π 2 + π · k, k ∈ Z.

Regangkan sepanjang O x 3 2 kali. Mari kita hitung tempoh positif terkecil, dan ia adalah sama dengan T = π k 2 = 3 2 π . Dan domain takrifan fungsi dengan koordinat ialah 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, hanya domain definisi berubah.

Simetri berlaku pada sisi O x. Tempoh tidak akan berubah pada ketika ini.

Ia adalah perlu untuk memaparkan paksi koordinat secara simetri. Domain definisi dalam kes ini tidak berubah. Jadual bertepatan dengan yang sebelumnya. Ini menunjukkan bahawa fungsi tangen adalah ganjil. Jika hendak fungsi ganjil tetapkan pemetaan simetri O x dan O y, kemudian tukar kepada fungsi asal.

Bergantung pada keadaan proses fizikal, beberapa kuantiti mengambil nilai tetap dan dipanggil pemalar, yang lain berubah dalam keadaan tertentu dan dipanggil pembolehubah.

Kajian Teliti persekitaran menunjukkan bahawa kuantiti fizik bergantung antara satu sama lain, iaitu perubahan dalam beberapa kuantiti memerlukan perubahan pada kuantiti yang lain.

Analisis matematik memperkatakan kajian tentang hubungan kuantitatif antara kuantiti yang berbeza-beza, mengabstraksikan daripada makna fizikal tertentu. Salah satu konsep asas analisis matematik ialah konsep fungsi.

Pertimbangkan unsur set dan unsur set
(Gamb. 3.1).

Jika beberapa surat-menyurat diwujudkan antara unsur-unsur set
Dan dalam bentuk peraturan , maka mereka perhatikan bahawa fungsi itu ditakrifkan
.

Definisi 3.1. Surat-menyurat , yang dikaitkan dengan setiap elemen bukan set kosong
beberapa elemen yang jelas bukan set kosong , dipanggil fungsi atau pemetaan
V .

Paparan secara simbolik
V ditulis seperti berikut:

.

Pada masa yang sama, ramai
dipanggil domain takrifan fungsi dan dilambangkan
.

Sebaliknya, ramai dipanggil julat nilai fungsi dan dilambangkan
.

Di samping itu, perlu diperhatikan bahawa unsur-unsur set
dipanggil pembolehubah bebas, unsur-unsur set dipanggil pembolehubah bersandar.

Kaedah untuk menentukan fungsi

Fungsi ini boleh ditentukan dalam cara utama berikut: jadual, grafik, analitik.

Jika, berdasarkan data eksperimen, jadual disusun yang mengandungi nilai fungsi dan nilai hujah yang sepadan, maka kaedah menentukan fungsi ini dipanggil jadual.

Pada masa yang sama, jika beberapa kajian hasil eksperimen dipaparkan pada perakam (osiloskop, perakam, dll.), maka diperhatikan bahawa fungsi itu dinyatakan secara grafik.

Yang paling biasa ialah cara analitik untuk menentukan fungsi, i.e. kaedah di mana pembolehubah bebas dan bersandar dikaitkan menggunakan formula. Dalam kes ini, domain takrifan fungsi memainkan peranan penting:

berbeza, walaupun ia diberikan oleh hubungan analitikal yang sama.

Jika anda hanya menentukan formula fungsi
, maka kami menganggap bahawa domain definisi fungsi ini bertepatan dengan set nilai pembolehubah tersebut , yang mana ungkapan
mempunyai makna. Dalam hal ini, masalah mencari domain definisi fungsi memainkan peranan yang istimewa.

Tugasan 3.1. Cari domain bagi suatu fungsi

Penyelesaian

Istilah pertama mengambil nilai sebenar apabila
, dan yang kedua di. Oleh itu, untuk mencari domain takrifan fungsi tertentu, adalah perlu untuk menyelesaikan sistem ketaksamaan:

Akibatnya, penyelesaian kepada sistem sedemikian diperolehi. Oleh itu, domain takrifan fungsi ialah segmen
.

Transformasi termudah bagi graf fungsi

Pembinaan graf fungsi boleh dipermudahkan dengan ketara jika anda menggunakan graf terkenal bagi fungsi asas asas. Fungsi berikut dipanggil fungsi asas utama:

1) fungsi kuasa
di mana
;

2) fungsi eksponen
di mana
Dan
;

3)fungsi logaritma
, Di mana -mana-mana nombor positif, berbeza daripada perpaduan:
Dan
;

4) fungsi trigonometri




;
.

5) fungsi trigonometri songsang
;
;
;
.

Fungsi asas ialah fungsi yang diperoleh daripada fungsi asas asas menggunakan empat operasi aritmetik dan superposisi digunakan beberapa kali terhingga.

Transformasi geometri mudah juga memungkinkan untuk memudahkan proses membina graf fungsi. Transformasi ini adalah berdasarkan kenyataan berikut:

Graf fungsi y=f(x+a) ialah graf y=f(x), dianjak (untuk a >0 ke kiri, untuk a< 0 вправо) на |a| единиц параллельно осиOx.

Graf fungsi y=f(x) +b ialah graf y=f(x), dianjak (pada b>0 ke atas, pada b< 0 вниз) на |b| единиц параллельно осиOy.

Graf bagi fungsi y = mf(x) (m0) ialah graf y = f(x), diregangkan (pada m>1) m kali atau dimampatkan (pada 0

Graf fungsi y = f(kx) ialah graf y = f(x), dimampatkan (untuk k >1) k kali atau diregangkan (untuk 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.