ഈ സേവനം ഉപയോഗിച്ച് നിങ്ങൾക്ക് കഴിയും ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യം കണ്ടെത്തുകവേഡിൽ ഫോർമാറ്റ് ചെയ്ത സൊല്യൂഷനോടുകൂടിയ ഒരു വേരിയബിൾ f(x). f(x,y) ഫംഗ്‌ഷൻ നൽകിയിട്ടുണ്ടെങ്കിൽ, രണ്ട് വേരിയബിളുകളുടെ ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീം കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. ഫംഗ്‌ഷനുകൾ കൂടുന്നതിന്റെയും കുറയുന്നതിന്റെയും ഇടവേളകളും നിങ്ങൾക്ക് കണ്ടെത്താനാകും.

ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യം കണ്ടെത്തുക

y =

വിഭാഗത്തിൽ [ ;]

സിദ്ധാന്തം ഉൾപ്പെടുത്തുക

ഫംഗ്ഷനുകൾ നൽകുന്നതിനുള്ള നിയമങ്ങൾ:

ഒരു വേരിയബിളിന്റെ ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീമിന് ആവശ്യമായ അവസ്ഥ

സമവാക്യം f" 0 (x *) = 0 ആണ് ആവശ്യമായ അവസ്ഥഒരു വേരിയബിളിന്റെ ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീം, അതായത്. പോയിന്റിൽ x * ഫംഗ്‌ഷന്റെ ആദ്യ ഡെറിവേറ്റീവ് അപ്രത്യക്ഷമാകണം. അത് എടുത്തുകാണിക്കുന്നു നിശ്ചല പോയിന്റുകൾ x s, ഇതിൽ പ്രവർത്തനം കൂടുകയോ കുറയുകയോ ചെയ്യില്ല.

ഒരു വേരിയബിളിന്റെ ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീമിന് മതിയായ അവസ്ഥ

F 0 (x) സെറ്റ് D-യിൽ പെടുന്ന x-നെ അപേക്ഷിച്ച് രണ്ടുതവണ വ്യത്യാസപ്പെട്ടിരിക്കട്ടെ. പോയിന്റ് x * ൽ വ്യവസ്ഥ പാലിക്കുകയാണെങ്കിൽ:

F" 0 (x *) = 0
f"" 0 (x *) > 0

അപ്പോൾ പോയിന്റ് x * എന്നത് ഫംഗ്‌ഷന്റെ പ്രാദേശിക (ആഗോള) ഏറ്റവും കുറഞ്ഞ പോയിന്റാണ്.

പോയിന്റ് x * ൽ വ്യവസ്ഥ പാലിക്കുകയാണെങ്കിൽ:

F" 0 (x *) = 0
f"" 0 (x *)< 0

അപ്പോൾ പോയിന്റ് x * ഒരു പ്രാദേശിക (ആഗോള) പരമാവധി ആണ്.

ഉദാഹരണം നമ്പർ 1. ഫംഗ്‌ഷന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യങ്ങൾ കണ്ടെത്തുക: സെഗ്‌മെന്റിൽ.
പരിഹാരം.

നിർണായക പോയിന്റ് ഒന്ന് x 1 = 2 (f'(x)=0) ആണ്. ഈ പോയിന്റ് വിഭാഗത്തിന്റേതാണ്. (0∉ എന്നതിനാൽ x=0 എന്ന പോയിന്റ് നിർണായകമല്ല).
സെഗ്‌മെന്റിന്റെ അറ്റത്തും നിർണായക പോയിന്റിലും ഞങ്ങൾ ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ കണക്കാക്കുന്നു.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
ഉത്തരം: f min = 5 / 2 at x=2; f max =9, x=1

ഉദാഹരണം നമ്പർ 2. ഉയർന്ന ഓർഡർ ഡെറിവേറ്റീവുകൾ ഉപയോഗിച്ച്, y=x-2sin(x) ഫംഗ്ഷന്റെ എക്സ്ട്രീം കണ്ടെത്തുക.
പരിഹാരം.
ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക: y'=1-2cos(x) . നമുക്ക് നിർണായക പോയിന്റുകൾ കണ്ടെത്താം: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. ഞങ്ങൾ y''=2sin(x), കണക്കാക്കുക , അതായത് x= π / 3 +2πk, k∈Z എന്നത് ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റുകളാണ്; , അതായത് x=- π / 3 +2πk, kZ എന്നിവയാണ് ഫംഗ്‌ഷന്റെ പരമാവധി പോയിന്റുകൾ.

ഉദാഹരണം നമ്പർ 3. x=0 എന്ന ബിന്ദുവിന് സമീപമുള്ള എക്സ്ട്രീം ഫംഗ്ഷൻ അന്വേഷിക്കുക.
പരിഹാരം. ഇവിടെ ഫംഗ്ഷന്റെ തീവ്രത കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. എക്സ്ട്രീം x=0 ആണെങ്കിൽ, അതിന്റെ തരം (കുറഞ്ഞത് അല്ലെങ്കിൽ കൂടിയത്) കണ്ടെത്തുക. കണ്ടെത്തിയ പോയിന്റുകളിൽ x = 0 ഇല്ലെങ്കിൽ, f(x=0) ഫംഗ്‌ഷന്റെ മൂല്യം കണക്കാക്കുക.
തന്നിരിക്കുന്ന ബിന്ദുവിന്റെ ഓരോ വശത്തുമുള്ള ഡെറിവേറ്റീവ് അതിന്റെ അടയാളം മാറ്റാത്തപ്പോൾ, സാധ്യമായ സാഹചര്യങ്ങൾ വ്യത്യസ്തമായ പ്രവർത്തനങ്ങൾക്ക് പോലും തീർന്നില്ല എന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്: ഇത് സംഭവിക്കാം x 0 എന്ന പോയിന്റിന്റെ ഒരു വശത്ത് ഏകപക്ഷീയമായി ചെറിയ അയൽപക്കത്തിന് ഇരുവശത്തും ഡെറിവേറ്റീവ് മാറ്റങ്ങളുടെ അടയാളം. ഈ ഘട്ടങ്ങളിൽ, ഒരു എക്സ്ട്രീമിലെ പ്രവർത്തനങ്ങൾ പഠിക്കാൻ മറ്റ് രീതികൾ ഉപയോഗിക്കേണ്ടത് ആവശ്യമാണ്.

ഒരു പ്രവർത്തനത്തിന്റെ സ്വഭാവം നിർണ്ണയിക്കാനും അതിന്റെ സ്വഭാവത്തെക്കുറിച്ച് സംസാരിക്കാനും, വർദ്ധനവിന്റെയും കുറവിന്റെയും ഇടവേളകൾ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. ഈ പ്രക്രിയയെ ഫംഗ്ഷൻ റിസർച്ച് ആൻഡ് ഗ്രാഫിംഗ് എന്ന് വിളിക്കുന്നു. ഒരു ഫംഗ്ഷന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യങ്ങൾ കണ്ടെത്തുമ്പോൾ എക്സ്ട്രീം പോയിന്റ് ഉപയോഗിക്കുന്നു, കാരണം അവയിൽ ഫംഗ്ഷൻ ഇടവേളയിൽ നിന്ന് കൂടുകയോ കുറയുകയോ ചെയ്യുന്നു.

ഈ ലേഖനം നിർവചനങ്ങൾ വെളിപ്പെടുത്തുന്നു, ഞങ്ങൾ രൂപപ്പെടുത്തുന്നു മതിയായ സൂചനഇടവേളയിൽ വർദ്ധനവും കുറവും ഒരു എക്സ്ട്രീം നിലനിൽപ്പിനുള്ള വ്യവസ്ഥയും. ഉദാഹരണങ്ങളും പ്രശ്നങ്ങളും പരിഹരിക്കുന്നതിന് ഇത് ബാധകമാണ്. ഫംഗ്‌ഷനുകളെ വേർതിരിക്കുന്ന വിഭാഗം ആവർത്തിക്കണം, കാരണം ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നതിന് പരിഹാരം ഉപയോഗിക്കേണ്ടതുണ്ട്.

Yandex.RTB R-A-339285-1 നിർവ്വചനം 1

ഏത് x 1 ∈ X, x 2 ∈ X, x 2 > x 1 എന്നിവയ്‌ക്ക് അസമത്വം f (x 2) > f (x 1) തൃപ്തിപ്പെടുമ്പോൾ x എന്ന ഇടവേളയിൽ y = f (x) ഫംഗ്‌ഷൻ വർദ്ധിക്കും. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ആർഗ്യുമെന്റിന്റെ വലിയ മൂല്യം ഫംഗ്ഷന്റെ വലിയ മൂല്യവുമായി പൊരുത്തപ്പെടുന്നു.

നിർവ്വചനം 2

ഏത് x 1 ∈ X, x 2 ∈ X, x 2 > x 1, തുല്യത f (x 2) > f (x 1) എന്നതിന് x ഇടവേളയിൽ y = f (x) ഫംഗ്‌ഷൻ കുറയുന്നതായി കണക്കാക്കുന്നു. സത്യമായി കണക്കാക്കപ്പെടുന്നു. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ഒരു വലിയ ഫംഗ്ഷൻ മൂല്യം ഒരു ചെറിയ ആർഗ്യുമെന്റ് മൂല്യവുമായി പൊരുത്തപ്പെടുന്നു. ചുവടെയുള്ള ചിത്രം പരിഗണിക്കുക.

അഭിപ്രായം: കൂടുന്നതിന്റെയും കുറയുന്നതിന്റെയും ഇടവേളയുടെ അറ്റത്ത് ഫംഗ്ഷൻ നിർണ്ണായകവും നിരന്തരവുമാകുമ്പോൾ, അതായത് (a; b), x = a, x = b, കൂടുന്നതിന്റെയും കുറയുന്നതിന്റെയും ഇടവേളയിൽ പോയിന്റുകൾ ഉൾപ്പെടുന്നു. ഇത് നിർവചനത്തിന് വിരുദ്ധമല്ല; ഇത് x ഇടവേളയിൽ നടക്കുന്നു എന്നാണ് ഇതിനർത്ഥം.

അടിസ്ഥാന ഗുണങ്ങൾ പ്രാഥമിക പ്രവർത്തനങ്ങൾടൈപ്പ് y = sin x - ആർഗ്യുമെന്റുകളുടെ യഥാർത്ഥ മൂല്യങ്ങൾക്കുള്ള നിർവചനവും തുടർച്ചയും. ഇടവേളയിൽ സൈൻ വർദ്ധിക്കുന്നതായി ഇവിടെ നിന്ന് നമുക്ക് ലഭിക്കുന്നു - π 2; π 2, അപ്പോൾ സെഗ്മെന്റിലെ വർദ്ധനവിന് ഫോം ഉണ്ട് - π 2; π 2.

നിർവ്വചനം 3

പോയിന്റ് x 0 എന്ന് വിളിക്കുന്നു പരമാവധി പോയിന്റ് y = f (x) എന്ന ഫംഗ്‌ഷനായി, x ന്റെ എല്ലാ മൂല്യങ്ങൾക്കും അസമത്വം f (x 0) ≥ f (x) സാധുവായിരിക്കുമ്പോൾ. പരമാവധി പ്രവർത്തനംഒരു ബിന്ദുവിലെ ഫംഗ്‌ഷന്റെ മൂല്യമാണ്, ഇത് y m a x കൊണ്ട് സൂചിപ്പിക്കുന്നു.

x ന്റെ എല്ലാ മൂല്യങ്ങൾക്കും അസമത്വം f (x 0) ≤ f (x) സാധുതയുള്ളപ്പോൾ, x 0 എന്ന പോയിന്റിനെ y = f (x) ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റ് എന്ന് വിളിക്കുന്നു. ഏറ്റവും കുറഞ്ഞ പ്രവർത്തനങ്ങൾഒരു പോയിന്റിലെ ഫംഗ്‌ഷന്റെ മൂല്യമാണ്, കൂടാതെ y m i n എന്ന രൂപത്തിന്റെ ഒരു പദവിയും ഉണ്ട്.

പോയിന്റ് x 0 ന്റെ അയൽപക്കങ്ങൾ പരിഗണിക്കപ്പെടുന്നു തീവ്ര പോയിന്റുകൾ,എക്സ്ട്രീം പോയിന്റുകളുമായി പൊരുത്തപ്പെടുന്ന ഫംഗ്ഷന്റെ മൂല്യവും. ചുവടെയുള്ള ചിത്രം പരിഗണിക്കുക.

ഏറ്റവും വലുതും ഉള്ളതുമായ ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീമ ഏറ്റവും കുറഞ്ഞ മൂല്യംപ്രവർത്തനങ്ങൾ. ചുവടെയുള്ള ചിത്രം പരിഗണിക്കുക.

സെഗ്‌മെന്റിൽ നിന്ന് ഫംഗ്‌ഷന്റെ ഏറ്റവും വലിയ മൂല്യം കണ്ടെത്തേണ്ടത് ആവശ്യമാണെന്ന് ആദ്യ ചിത്രം പറയുന്നു [a; ബി ]. ഇത് പരമാവധി പോയിന്റുകൾ ഉപയോഗിച്ചാണ് കണ്ടെത്തുന്നത്, ഇത് ഫംഗ്ഷന്റെ പരമാവധി മൂല്യത്തിന് തുല്യമാണ്, രണ്ടാമത്തെ ചിത്രം x = b-ൽ പരമാവധി പോയിന്റ് കണ്ടെത്തുന്നത് പോലെയാണ്.

ഒരു ഫംഗ്‌ഷൻ കൂട്ടുന്നതിനും കുറയുന്നതിനും മതിയായ വ്യവസ്ഥകൾ

ഒരു ഫംഗ്‌ഷന്റെ മാക്‌സിമയും മിനിമയും കണ്ടെത്താൻ, ഫംഗ്‌ഷൻ ഈ വ്യവസ്ഥകൾ പാലിക്കുമ്പോൾ, അത്യന്തം അടയാളങ്ങൾ പ്രയോഗിക്കേണ്ടത് ആവശ്യമാണ്. ആദ്യത്തെ അടയാളം ഏറ്റവും കൂടുതൽ ഉപയോഗിക്കുന്നതായി കണക്കാക്കപ്പെടുന്നു.

ഒരു തീവ്രതയ്ക്ക് ആവശ്യമായ ആദ്യത്തെ വ്യവസ്ഥ

നിർവ്വചനം 4

ഒരു ഫംഗ്‌ഷൻ y = f (x) നൽകട്ടെ, അത് x 0 പോയിന്റിന്റെ ε അയൽപക്കത്തിൽ വേർതിരിക്കാവുന്നതും തന്നിരിക്കുന്ന പോയിന്റിൽ x 0 ന് തുടർച്ചയുള്ളതുമാണ്. ഇവിടെ നിന്ന് നമുക്ക് അത് ലഭിക്കും

• x ∈ (x 0 - ε ; x 0), f " (x) എന്നിവയ്‌ക്കൊപ്പം f "(x) > 0 ആയിരിക്കുമ്പോൾ< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• എപ്പോൾ f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >x ∈ (x 0 ; x 0 + ε) ന് 0, തുടർന്ന് x 0 ആണ് ഏറ്റവും കുറഞ്ഞ പോയിന്റ്.

മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, അടയാളം സജ്ജീകരിക്കുന്നതിന് ഞങ്ങൾ അവരുടെ വ്യവസ്ഥകൾ നേടുന്നു:

• x 0 എന്ന ബിന്ദുവിൽ ഫംഗ്‌ഷൻ തുടർച്ചയായിരിക്കുമ്പോൾ, അതിന് മാറുന്ന ചിഹ്നമുള്ള ഒരു ഡെറിവേറ്റീവ് ഉണ്ട്, അതായത് + മുതൽ - വരെ, അതായത് പോയിന്റിനെ പരമാവധി എന്ന് വിളിക്കുന്നു;
• x 0 എന്ന ബിന്ദുവിൽ ഫംഗ്‌ഷൻ തുടർച്ചയായി ആയിരിക്കുമ്പോൾ, അതിന് - മുതൽ + വരെ മാറുന്ന ചിഹ്നമുള്ള ഒരു ഡെറിവേറ്റീവ് ഉണ്ട്, അതായത് പോയിന്റിനെ മിനിമം എന്ന് വിളിക്കുന്നു.

ഒരു ഫംഗ്‌ഷന്റെ പരമാവധി, കുറഞ്ഞ പോയിന്റുകൾ ശരിയായി നിർണ്ണയിക്കാൻ, അവ കണ്ടെത്തുന്നതിന് നിങ്ങൾ അൽ‌ഗോരിതം പാലിക്കണം:

• നിർവചനത്തിന്റെ ഡൊമെയ്ൻ കണ്ടെത്തുക;
• ഈ മേഖലയിലെ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തുക;
• ഫംഗ്ഷൻ നിലവിലില്ലാത്ത പൂജ്യങ്ങളും പോയിന്റുകളും തിരിച്ചറിയുക;
• ഇടവേളകളിൽ ഡെറിവേറ്റീവിന്റെ അടയാളം നിർണ്ണയിക്കുന്നു;
• ഫംഗ്ഷൻ അടയാളം മാറ്റുന്ന പോയിന്റുകൾ തിരഞ്ഞെടുക്കുക.

ഒരു ഫംഗ്ഷന്റെ തീവ്രത കണ്ടെത്തുന്നതിനുള്ള നിരവധി ഉദാഹരണങ്ങൾ പരിഹരിച്ചുകൊണ്ട് അൽഗോരിതം പരിഗണിക്കാം.

ഉദാഹരണം 1

തന്നിരിക്കുന്ന ഫംഗ്‌ഷന്റെ പരമാവധി കുറഞ്ഞ പോയിന്റുകൾ കണ്ടെത്തുക y = 2 (x + 1) 2 x - 2 .

പരിഹാരം

തന്നിരിക്കുന്ന പ്രവർത്തനത്തിന്റെ വ്യാപ്തി എല്ലാമാണ് യഥാർത്ഥ സംഖ്യകൾ x = 2 ഒഴികെ. ആദ്യം, നമുക്ക് ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്തി നേടാം:

y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2 ) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

ഫംഗ്‌ഷന്റെ പൂജ്യങ്ങൾ x = - 1, x = 5, x = 2 ആണെന്ന് ഇവിടെ നിന്ന് നമുക്ക് കാണാം, അതായത്, ഓരോ ബ്രാക്കറ്റും പൂജ്യത്തിന് തുല്യമായിരിക്കണം. നമുക്ക് ഇത് നമ്പർ അക്ഷത്തിൽ അടയാളപ്പെടുത്തി നേടാം:

ഇപ്പോൾ നമ്മൾ ഓരോ ഇടവേളയിൽ നിന്നും ഡെറിവേറ്റീവിന്റെ അടയാളങ്ങൾ നിർണ്ണയിക്കുന്നു. ഇടവേളയിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന ഒരു പോയിന്റ് തിരഞ്ഞെടുത്ത് അത് എക്സ്പ്രഷനിലേക്ക് പകരം വയ്ക്കേണ്ടത് ആവശ്യമാണ്. ഉദാഹരണത്തിന്, പോയിന്റുകൾ x = - 2, x = 0, x = 3, x = 6.

ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, അതായത് ഇടവേള - ∞ ; - 1 ന് പോസിറ്റീവ് ഡെറിവേറ്റീവ് ഉണ്ട്. അതുപോലെ, ഞങ്ങൾ അത് കണ്ടെത്തുന്നു

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

രണ്ടാമത്തെ ഇടവേള പൂജ്യത്തേക്കാൾ കുറവായതിനാൽ, ഇടവേളയിലെ ഡെറിവേറ്റീവ് നെഗറ്റീവ് ആയിരിക്കുമെന്നാണ് ഇതിനർത്ഥം. മൂന്നാമത്തേത് മൈനസ്, നാലാമത്തേത് പ്ലസ്. തുടർച്ച നിർണ്ണയിക്കാൻ, ഡെറിവേറ്റീവിന്റെ അടയാളം നിങ്ങൾ ശ്രദ്ധിക്കേണ്ടതുണ്ട്; അത് മാറുകയാണെങ്കിൽ, ഇത് ഒരു എക്സ്ട്രീം പോയിന്റാണ്.

x = - 1 എന്ന പോയിന്റിൽ ഫംഗ്‌ഷൻ തുടർച്ചയായിരിക്കുമെന്ന് ഞങ്ങൾ കണ്ടെത്തുന്നു, അതായത് ഡെറിവേറ്റീവ് ചിഹ്നം + മുതൽ - വരെ മാറ്റും. ആദ്യത്തെ അടയാളം അനുസരിച്ച്, നമുക്ക് x = - 1 ഒരു പരമാവധി പോയിന്റാണ്, അതായത് നമുക്ക് ലഭിക്കുന്നു

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

x = 5 എന്ന പോയിന്റ് ഫംഗ്‌ഷൻ തുടർച്ചയാണെന്ന് സൂചിപ്പിക്കുന്നു, കൂടാതെ ഡെറിവേറ്റീവ് ചിഹ്നം – മുതൽ + വരെ മാറും. ഇതിനർത്ഥം x = -1 ആണ് ഏറ്റവും കുറഞ്ഞ പോയിന്റ്, അതിന്റെ നിർണ്ണയത്തിന് ഒരു രൂപമുണ്ട്

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

ഗ്രാഫിക് ചിത്രം

ഉത്തരം: y m a x = y (- 1) = 0, y m i n = y (5) = 24.

ഒരു എക്സ്ട്രീമിന് മതിയായ ആദ്യത്തെ മാനദണ്ഡം ഉപയോഗിക്കുന്നതിന് x 0 പോയിന്റിലെ ഫംഗ്ഷന്റെ വ്യത്യാസം ആവശ്യമില്ല എന്ന വസ്തുത ശ്രദ്ധിക്കേണ്ടതാണ്, ഇത് കണക്കുകൂട്ടൽ ലളിതമാക്കുന്നു.

ഉദാഹരണം 2

y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 എന്ന ഫംഗ്‌ഷന്റെ പരമാവധി, കുറഞ്ഞ പോയിന്റുകൾ കണ്ടെത്തുക.

പരിഹാരം.

ഒരു ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌ൻ എല്ലാം യഥാർത്ഥ സംഖ്യകളാണ്. ഫോമിന്റെ സമവാക്യങ്ങളുടെ ഒരു സിസ്റ്റമായി ഇത് എഴുതാം:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

തുടർന്ന് നിങ്ങൾ ഡെറിവേറ്റീവ് കണ്ടെത്തേണ്ടതുണ്ട്:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

പോയിന്റ് x = 0 ന് ഒരു ഡെറിവേറ്റീവ് ഇല്ല, കാരണം ഏകപക്ഷീയമായ പരിധികളുടെ മൂല്യങ്ങൾ വ്യത്യസ്തമാണ്. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 ലിം y "x → 0 + 0 = ലിം y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

x = 0 എന്ന പോയിന്റിൽ പ്രവർത്തനം തുടർച്ചയായി തുടരുന്നു, തുടർന്ന് ഞങ്ങൾ കണക്കാക്കുന്നു

lim y x → 0 - 0 = ലിം x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 ലിം y x → 0 + 0 = ലിം x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

ഡെറിവേറ്റീവ് പൂജ്യമാകുമ്പോൾ ആർഗ്യുമെന്റിന്റെ മൂല്യം കണ്ടെത്തുന്നതിന് കണക്കുകൂട്ടലുകൾ നടത്തേണ്ടത് ആവശ്യമാണ്:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

ഓരോ ഇടവേളയുടെയും അടയാളം നിർണ്ണയിക്കാൻ ലഭിച്ച എല്ലാ പോയിന്റുകളും ഒരു നേർരേഖയിൽ അടയാളപ്പെടുത്തിയിരിക്കണം. അതിനാൽ, ഓരോ ഇടവേളയ്ക്കും അനിയന്ത്രിതമായ പോയിന്റുകളിൽ ഡെറിവേറ്റീവ് കണക്കാക്കേണ്ടത് ആവശ്യമാണ്. ഉദാഹരണത്തിന്, നമുക്ക് x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6 മൂല്യങ്ങളുള്ള പോയിന്റുകൾ എടുക്കാം. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

നേർരേഖയിലെ ചിത്രം ഇതുപോലെ കാണപ്പെടുന്നു

ഇതിനർത്ഥം, ഒരു തീവ്രതയുടെ ആദ്യ അടയാളം അവലംബിക്കേണ്ടത് ആവശ്യമാണെന്ന നിഗമനത്തിൽ ഞങ്ങൾ എത്തിച്ചേരുന്നു എന്നാണ്. നമുക്ക് അത് കണക്കാക്കി കണ്ടെത്താം

x = - 4 - 2 3 3, x = 0, x = 4 + 2 3 3, തുടർന്ന് ഇവിടെ നിന്ന് പരമാവധി പോയിന്റുകൾക്ക് x = - 4 + 2 3 3, x = 4 - 2 3 3 മൂല്യങ്ങളുണ്ട്

മിനിമം കണക്കാക്കുന്നതിലേക്ക് പോകാം:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

ഫംഗ്ഷന്റെ മാക്സിമ കണക്കാക്കാം. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

ഗ്രാഫിക് ചിത്രം

ഉത്തരം:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 y 27 = y 4 - 2 3 3 = 8 27 3

f " (x 0) = 0 എന്ന ഫംഗ്‌ഷൻ നൽകിയിട്ടുണ്ടെങ്കിൽ, f "" (x 0) > 0 ആണെങ്കിൽ, f "" (x 0) ആണെങ്കിൽ x 0 ആണ് ഏറ്റവും കുറഞ്ഞ പോയിന്റ് എന്ന് നമുക്ക് ലഭിക്കും.< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

ഉദാഹരണം 3

y = 8 x x + 1 ഫംഗ്‌ഷന്റെ മാക്സിമയും മിനിമയും കണ്ടെത്തുക.

പരിഹാരം

ആദ്യം, ഞങ്ങൾ നിർവചനത്തിന്റെ ഡൊമെയ്ൻ കണ്ടെത്തുന്നു. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

D(y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

ഫംഗ്ഷൻ വേർതിരിക്കേണ്ടത് ആവശ്യമാണ്, അതിനുശേഷം നമുക്ക് ലഭിക്കുന്നു

y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

x = 1-ൽ, ഡെറിവേറ്റീവ് പൂജ്യമായി മാറുന്നു, അതായത് പോയിന്റ് സാധ്യമായ ഒരു തീവ്രതയാണ്. വ്യക്തമാക്കുന്നതിന്, രണ്ടാമത്തെ ഡെറിവേറ്റീവ് കണ്ടെത്തുകയും മൂല്യം x = 1-ൽ കണക്കാക്കുകയും ചെയ്യേണ്ടത് ആവശ്യമാണ്. നമുക്ക് ലഭിക്കുന്നത്:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2 "x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0

ഇതിനർത്ഥം, ഒരു എക്സ്ട്രീമിന് മതിയായ 2 വ്യവസ്ഥ ഉപയോഗിക്കുമ്പോൾ, x = 1 ഒരു പരമാവധി പോയിന്റാണെന്ന് നമുക്ക് ലഭിക്കും. അല്ലെങ്കിൽ, എൻട്രി y m a x = y (1) = 8 1 1 + 1 = 4 പോലെ കാണപ്പെടുന്നു.

ഗ്രാഫിക് ചിത്രം

ഉത്തരം: y m a x = y (1) = 4 ..

നിർവ്വചനം 5

y = f (x) എന്ന ഫംഗ്‌ഷന് തന്നിരിക്കുന്ന പോയിന്റ് x 0-ന്റെ ε അയൽപക്കത്തിൽ n-ആം ക്രമം വരെയും അതിന്റെ ഡെറിവേറ്റീവ് x 0 പോയിന്റിലെ n + 1st ഓർഡർ വരെയും ഉണ്ട്. അപ്പോൾ f " (x 0) = f "" (x 0) = f "" " (x 0) = . . . = f n (x 0) = 0 .

n ഒരു ഇരട്ട സംഖ്യയായിരിക്കുമ്പോൾ, x 0 ഒരു ഇൻഫ്‌ളക്ഷൻ പോയിന്റായി കണക്കാക്കപ്പെടുന്നു, n ഒരു ഒറ്റ സംഖ്യയാണെങ്കിൽ, x 0 ഒരു തീവ്ര ബിന്ദുവാണ്, f (n + 1) (x 0) > 0, തുടർന്ന് x 0 എന്നത് ഏറ്റവും കുറഞ്ഞ പോയിന്റാണ്, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.

ഉദാഹരണം 4

y y = 1 16 (x + 1) 3 (x - 3) 4 ഫംഗ്‌ഷന്റെ പരമാവധി, കുറഞ്ഞ പോയിന്റുകൾ കണ്ടെത്തുക.

പരിഹാരം

യഥാർത്ഥ ഫംഗ്‌ഷൻ ഒരു യുക്തിസഹമായ മുഴുവൻ ഫംഗ്‌ഷനാണ്, അതിനർത്ഥം നിർവചനത്തിന്റെ ഡൊമെയ്‌ൻ എല്ലാ യഥാർത്ഥ സംഖ്യകളാണെന്നാണ്. പ്രവർത്തനത്തെ വേർതിരിക്കേണ്ടത് ആവശ്യമാണ്. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

ഈ ഡെറിവേറ്റീവ് x 1 = - 1, x 2 = 5 7, x 3 = 3 എന്നതിൽ പൂജ്യത്തിലേക്ക് പോകും. അതായത്, പോയിന്റുകൾ സാധ്യമായ എക്സ്ട്രീം പോയിന്റുകളാകാം. തീവ്രതയ്ക്ക് മൂന്നാമത്തെ മതിയായ വ്യവസ്ഥ പ്രയോഗിക്കേണ്ടത് ആവശ്യമാണ്. രണ്ടാമത്തെ ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നത് ഒരു ഫംഗ്ഷന്റെ പരമാവധി, കുറഞ്ഞ സാന്നിധ്യം കൃത്യമായി നിർണ്ണയിക്കാൻ നിങ്ങളെ അനുവദിക്കുന്നു. രണ്ടാമത്തെ ഡെറിവേറ്റീവ് അതിന്റെ സാധ്യമായ തീവ്രതയുടെ പോയിന്റുകളിൽ കണക്കാക്കുന്നു. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

ഇതിനർത്ഥം x 2 = 5 7 ആണ് പരമാവധി പോയിന്റ്. മൂന്നാമത്തെ മതിയായ മാനദണ്ഡം പ്രയോഗിച്ചാൽ, n = 1, f (n + 1) 5 7 എന്നിവയ്‌ക്കായി ഞങ്ങൾ അത് നേടുന്നു.< 0 .

x 1 = - 1, x 3 = 3 പോയിന്റുകളുടെ സ്വഭാവം നിർണ്ണയിക്കേണ്ടത് ആവശ്യമാണ്. ഇത് ചെയ്യുന്നതിന്, നിങ്ങൾ മൂന്നാമത്തെ ഡെറിവേറ്റീവ് കണ്ടെത്തി ഈ പോയിന്റുകളിലെ മൂല്യങ്ങൾ കണക്കാക്കേണ്ടതുണ്ട്. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y "" " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y """ (- 1) = 96 ≠ 0 y "" " (3) = 0

ഇതിനർത്ഥം, n = 2, f (n + 1) (- 1) ≠ 0 എന്നിവയ്‌ക്ക് x 1 = - 1 എന്നത് ഫംഗ്‌ഷന്റെ ഇൻഫ്‌ളക്ഷൻ പോയിന്റാണ്. പോയിന്റ് x 3 = 3 അന്വേഷിക്കേണ്ടത് ആവശ്യമാണ്. ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ നാലാമത്തെ ഡെറിവേറ്റീവ് കണ്ടെത്തുകയും ഈ ഘട്ടത്തിൽ കണക്കുകൂട്ടലുകൾ നടത്തുകയും ചെയ്യുന്നു:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

മുകളിൽ തീരുമാനിച്ചതിൽ നിന്ന്, x 3 = 3 ഫംഗ്ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റാണെന്ന് ഞങ്ങൾ നിഗമനം ചെയ്യുന്നു.

ഗ്രാഫിക് ചിത്രം

ഉത്തരം: x 2 = 5 7 ആണ് പരമാവധി പോയിന്റ്, നൽകിയിരിക്കുന്ന ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ പോയിന്റ് x 3 = 3 ആണ്.

ടെക്‌സ്‌റ്റിൽ ഒരു പിശക് നിങ്ങൾ ശ്രദ്ധയിൽപ്പെട്ടാൽ, അത് ഹൈലൈറ്റ് ചെയ്‌ത് Ctrl+Enter അമർത്തുക

>> എക്സ്ട്രീമ

പ്രവർത്തനത്തിന്റെ അതിരുകടന്ന ഭാഗം

തീവ്രതയുടെ നിർവ്വചനം

ഫംഗ്ഷൻ y = f(x) എന്ന് വിളിക്കുന്നു വർദ്ധിച്ചുവരുന്ന (കുറയുന്നു) ഒരു നിശ്ചിത ഇടവേളയിൽ, x 1 ആണെങ്കിൽ< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).

ഒരു ഇടവേളയിൽ ഡിഫറൻഷ്യബിൾ ഫംഗ്‌ഷൻ y = f (x) വർദ്ധിക്കുകയാണെങ്കിൽ (കുറയുന്നു), ഈ ഇടവേളയിൽ അതിന്റെ ഡെറിവേറ്റീവ് f " (x)> 0

(f"(x)< 0).

ഡോട്ട് x ഒ വിളിച്ചു പ്രാദേശിക പരമാവധി പോയിന്റ് (ഏറ്റവും കുറഞ്ഞത്) ഫംഗ്‌ഷൻ f (x) പോയിന്റിന്റെ അയൽപക്കമുണ്ടെങ്കിൽ x ഒ, അസമത്വത്തിന്റെ എല്ലാ പോയിന്റുകൾക്കും f (x) ശരിയാണ്≤ f (x o) (f (x)≥ f (x o )).

പരമാവധി, കുറഞ്ഞ പോയിന്റുകൾ വിളിക്കുന്നു അങ്ങേയറ്റത്തെ പോയിന്റുകൾ, ഈ പോയിന്റുകളിലെ ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ അതിന്റെതാണ് അങ്ങേയറ്റം.

എക്സ്ട്രീം പോയിന്റുകൾ

ഒരു തീവ്രതയ്ക്ക് ആവശ്യമായ വ്യവസ്ഥകൾ . പോയിന്റ് ആണെങ്കിൽ x ഒ f (x) ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീം പോയിന്റാണ്, പിന്നെ ഒന്നുകിൽ f " (x o ) = 0, അല്ലെങ്കിൽ f(x o ) നിലവിലില്ല. അത്തരം പോയിന്റുകൾ വിളിക്കുന്നു വിമർശനാത്മകമായ,കൂടാതെ ഫംഗ്ഷൻ തന്നെ നിർണായക ഘട്ടത്തിൽ നിർവചിക്കപ്പെടുന്നു. ഒരു ഫംഗ്‌ഷന്റെ തീവ്രത അതിന്റെ നിർണായക പോയിന്റുകൾക്കിടയിൽ അന്വേഷിക്കണം.

ആദ്യത്തെ മതിയായ അവസ്ഥ. അനുവദിക്കുക x ഒ - നിര്ണ്ണായക ബിന്ദു. എങ്കിൽ f" (x) ഒരു പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ x ഒ പ്ലസ് ചിഹ്നം മൈനസിലേക്ക് മാറ്റുന്നു, തുടർന്ന് പോയിന്റിൽ x ഒഫംഗ്‌ഷന് പരമാവധി ഉണ്ട്, അല്ലെങ്കിൽ അതിന് മിനിമം ഉണ്ട്. നിർണായക പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ, ഡെറിവേറ്റീവ് ചിഹ്നം മാറ്റുന്നില്ലെങ്കിൽ, പോയിന്റിൽ x ഒ അങ്ങേയറ്റം ഇല്ല.

രണ്ടാമത്തെ മതിയായ അവസ്ഥ. f(x) ഫംഗ്‌ഷൻ ഉണ്ടായിരിക്കട്ടെ
f" (x ) പോയിന്റിന് സമീപം x ഒ പോയിന്റിൽ തന്നെയുള്ള രണ്ടാമത്തെ ഡെറിവേറ്റീവും x ഒ. എങ്കിൽ f"(x ഒ) = 0, >0 ( <0), то точка x ഒ f (x) ഫംഗ്‌ഷന്റെ പ്രാദേശിക മിനിമം (പരമാവധി) പോയിന്റാണ്. =0 ആണെങ്കിൽ, ഒന്നുകിൽ നിങ്ങൾ ആദ്യത്തെ മതിയായ അവസ്ഥ ഉപയോഗിക്കേണ്ടതുണ്ട് അല്ലെങ്കിൽ ഉയർന്നത് ഉൾപ്പെടുത്തണം.

ഒരു സെഗ്‌മെന്റിൽ, y = f (x) ഫംഗ്‌ഷന് അതിന്റെ ഏറ്റവും കുറഞ്ഞ അല്ലെങ്കിൽ കൂടിയ മൂല്യത്തിൽ നിർണായക പോയിന്റുകളിലോ സെഗ്‌മെന്റിന്റെ അറ്റത്തോ എത്താൻ കഴിയും.

ഉദാഹരണം 3.22.

പരിഹാരം.കാരണം എഫ് " (

ഒരു ഫംഗ്ഷന്റെ എക്സ്ട്രീം കണ്ടെത്തുന്നതിലെ പ്രശ്നങ്ങൾ

ഉദാഹരണം 3.23. എ

പരിഹാരം. xഒപ്പം വൈ വൈ
0 ≤ x≤
> 0, എപ്പോൾ x >a /4 എസ് " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение പ്രവർത്തനങ്ങൾ കെ.വി. യൂണിറ്റുകൾ).

ഉദാഹരണം 3.24. p ≈

പരിഹാരം.പി പി
എസ്"
R = 2, H = 16/4 = 4.

ഉദാഹരണം 3.22.f (x) = 2x 3 - 15x 2 + 36x - 14 ഫംഗ്‌ഷന്റെ തീവ്രത കണ്ടെത്തുക.

പരിഹാരം.കാരണം എഫ് " (x ) = 6x 2 - 30x +36 = 6(x ​​-2)(x - 3), തുടർന്ന് ഫംഗ്‌ഷന്റെ നിർണായക പോയിന്റുകൾ x 1 = 2, x 2 = 3. എക്സ്ട്രീമ ഈ പോയിന്റുകളിൽ മാത്രമേ ഉണ്ടാകൂ. x 1 = 2 എന്ന പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ ഡെറിവേറ്റീവ് ചിഹ്നം പ്ലസ് മുതൽ മൈനസിലേക്ക് മാറുന്നു, ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന് പരമാവധി ഉണ്ട്. x 2 = 3 എന്ന പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ, ഡെറിവേറ്റീവ് അതിന്റെ ചിഹ്നത്തെ മൈനസിൽ നിന്ന് പ്ലസിലേക്ക് മാറ്റുന്നു, അതിനാൽ x 2 = 3 പോയിന്റിൽ ഫംഗ്‌ഷന് മിനിമം ഉണ്ട്. പോയിന്റുകളിലെ പ്രവർത്തന മൂല്യങ്ങൾ കണക്കാക്കുന്നു
x 1 = 2 ഉം x 2 = 3 ഉം, ഫംഗ്‌ഷന്റെ തീവ്രത ഞങ്ങൾ കണ്ടെത്തുന്നു: പരമാവധി f (2) = 14, ഏറ്റവും കുറഞ്ഞ എഫ് (3) = 13.

ഉദാഹരണം 3.23.കൽഭിത്തിക്ക് സമീപം ചതുരാകൃതിയിലുള്ള ഒരു പ്രദേശം നിർമ്മിക്കേണ്ടത് ആവശ്യമാണ്, അങ്ങനെ അത് മൂന്ന് വശങ്ങളിൽ വയർ മെഷ് ഉപയോഗിച്ച് വേലി കെട്ടി, നാലാമത്തെ വശം മതിലിനോട് ചേർന്നാണ്. ഇതിനായി ഉണ്ട് എമെഷിന്റെ ലീനിയർ മീറ്റർ. ഏത് വീക്ഷണാനുപാതത്തിലാണ് സൈറ്റിന് ഏറ്റവും വലിയ വിസ്തീർണ്ണമുള്ളത്?

പരിഹാരം.നമുക്ക് പ്ലാറ്റ്‌ഫോമിന്റെ വശങ്ങൾ സൂചിപ്പിക്കാം xഒപ്പം വൈ. സൈറ്റിന്റെ വിസ്തീർണ്ണം S = xy ആണ്. അനുവദിക്കുക വൈ- ഇത് മതിലിനോട് ചേർന്നുള്ള വശത്തിന്റെ നീളമാണ്. തുടർന്ന്, വ്യവസ്ഥയനുസരിച്ച്, 2x + y = a എന്ന തുല്യത തൃപ്തിപ്പെടുത്തണം. അതിനാൽ y = a - 2x, S = x (a - 2x), എവിടെ
0 ≤ x≤ a /2 (ഏരിയയുടെ നീളവും വീതിയും നെഗറ്റീവ് ആയിരിക്കരുത്). S " = a - 4x, a - 4x = 0 at x = a/4, എവിടെ നിന്ന്
y = a - 2 × a/4 =a/2. എന്തുകൊണ്ടെന്നാല് x = a /4 മാത്രമാണ് നിർണായക പോയിന്റ്; ഈ പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ ഡെറിവേറ്റീവിന്റെ അടയാളം മാറുന്നുണ്ടോയെന്ന് പരിശോധിക്കാം. x a /4 S "> 0, എപ്പോൾ x >a /4 എസ് " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение പ്രവർത്തനങ്ങൾ S(a/4) = a/4(a - a/2) = a 2/8 (കെ.വി. യൂണിറ്റുകൾ). S തുടർച്ചയായി ഓണായിരിക്കുകയും അതിന്റെ അറ്റങ്ങളിൽ S(0), S(a /2) എന്നിവ പൂജ്യത്തിന് തുല്യമായതിനാൽ, കണ്ടെത്തുന്ന മൂല്യം ഇതായിരിക്കും ഏറ്റവും ഉയർന്ന മൂല്യംപ്രവർത്തനങ്ങൾ. അതിനാൽ, പ്രശ്നത്തിന്റെ നൽകിയിരിക്കുന്ന വ്യവസ്ഥകളിൽ സൈറ്റിന്റെ ഏറ്റവും അനുകൂലമായ വീക്ഷണ അനുപാതം y = 2x ആണ്.

ഉദാഹരണം 3.24.V=16 ശേഷിയുള്ള ഒരു അടച്ച സിലിണ്ടർ ടാങ്ക് നിർമ്മിക്കേണ്ടത് ആവശ്യമാണ് p ≈ 50 മീ 3. ടാങ്കിന്റെ അളവുകൾ എന്തായിരിക്കണം (ആരം R ഉം ഉയരവും H) അതിനാൽ അതിന്റെ നിർമ്മാണത്തിന് ഏറ്റവും കുറഞ്ഞ അളവിലുള്ള മെറ്റീരിയൽ ഉപയോഗിക്കണം?

പരിഹാരം.സിലിണ്ടറിന്റെ മൊത്തം ഉപരിതല വിസ്തീർണ്ണം S = 2 ആണ്പി R(R+H). സിലിണ്ടറിന്റെ അളവ് നമുക്ക് അറിയാം V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R2 = 16/R2. അതിനാൽ S(R) = 2പി (R 2 +16/R). ഈ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് ഞങ്ങൾ കണ്ടെത്തുന്നു:
എസ്"(R) = 2 p (2R- 16/R 2) = 4 p (R- 8/R 2). എസ്" (R) = 0, R 3 = 8, അതിനാൽ,
R = 2, H = 16/4 = 4.

ഒരു ഫംഗ്‌ഷന്റെ വർദ്ധനവ്, കുറയൽ, തീവ്രത

ഒരു ഫംഗ്‌ഷന്റെ വർദ്ധനവ്, കുറയ്‌ക്കൽ, തീവ്രത എന്നിവയുടെ ഇടവേളകൾ കണ്ടെത്തുന്നത് ഒരു സ്വതന്ത്ര ചുമതലയും മറ്റ് ജോലികളുടെ ഒരു പ്രധാന ഭാഗവുമാണ്, പ്രത്യേകിച്ചും, പൂർണ്ണ പ്രവർത്തന പഠനം. പ്രവർത്തനത്തിന്റെ വർദ്ധനവ്, കുറവ്, തീവ്രത എന്നിവയെക്കുറിച്ചുള്ള പ്രാഥമിക വിവരങ്ങൾ നൽകിയിരിക്കുന്നു ഡെറിവേറ്റീവിനെക്കുറിച്ചുള്ള സൈദ്ധാന്തിക അധ്യായം, പ്രാഥമിക പഠനത്തിനായി ഞാൻ വളരെ ശുപാർശ ചെയ്യുന്നു (അല്ലെങ്കിൽ ആവർത്തനം)- ഇനിപ്പറയുന്ന മെറ്റീരിയൽ വളരെ അടിസ്ഥാനമാക്കിയുള്ളതാണ് എന്ന കാരണത്താലും അടിസ്ഥാനപരമായി ഡെറിവേറ്റീവ്,ഈ ലേഖനത്തിന്റെ യോജിപ്പുള്ള തുടർച്ചയാണ്. സമയം കുറവാണെങ്കിലും, ഇന്നത്തെ പാഠത്തിൽ നിന്നുള്ള ഉദാഹരണങ്ങളുടെ ഔപചാരികമായ പരിശീലനവും സാധ്യമാണ്.

ഇന്ന് അന്തരീക്ഷത്തിൽ അപൂർവമായ ഏകാഭിപ്രായത്തിന്റെ ഒരു ആത്മാവുണ്ട്, അവിടെയുള്ള എല്ലാവരും ആഗ്രഹത്താൽ ജ്വലിക്കുന്നതായി എനിക്ക് നേരിട്ട് അനുഭവപ്പെടുന്നു. ഒരു ഫംഗ്‌ഷൻ അതിന്റെ ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് പര്യവേക്ഷണം ചെയ്യാൻ പഠിക്കുക. അതിനാൽ, ന്യായമായ, നല്ല, ശാശ്വതമായ പദാവലി ഉടൻ നിങ്ങളുടെ മോണിറ്റർ സ്ക്രീനുകളിൽ ദൃശ്യമാകും.

എന്തിനുവേണ്ടി? ഒരു കാരണം ഏറ്റവും പ്രായോഗികമാണ്: ഒരു പ്രത്യേക ജോലിയിൽ പൊതുവെ എന്താണ് നിങ്ങളോട് ആവശ്യപ്പെടുന്നതെന്ന് വ്യക്തമാകും!

പ്രവർത്തനത്തിന്റെ ഏകതാനത. ഒരു ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകളും എക്‌സ്ട്രീമയും

നമുക്ക് ചില പ്രവർത്തനങ്ങൾ പരിഗണിക്കാം. ലളിതമായി പറഞ്ഞാൽ, അവൾ എന്ന് ഞങ്ങൾ അനുമാനിക്കുന്നു തുടർച്ചയായമുഴുവൻ നമ്പർ ലൈനിൽ:

അങ്ങനെയെങ്കിൽ, സാധ്യമായ മിഥ്യാധാരണകളിൽ നിന്ന് ഉടനടി രക്ഷപ്പെടാം, പ്രത്യേകിച്ചും അടുത്തിടെ പരിചയപ്പെട്ട വായനക്കാർക്ക് പ്രവർത്തനത്തിന്റെ സ്ഥിരമായ ചിഹ്നത്തിന്റെ ഇടവേളകൾ. ഇപ്പോൾ ഞങ്ങൾ താൽപ്പര്യമില്ല, ഫംഗ്‌ഷന്റെ ഗ്രാഫ് അച്ചുതണ്ടുമായി ബന്ധപ്പെട്ടിരിക്കുന്നതെങ്ങനെ (മുകളിൽ, താഴെ, അച്ചുതണ്ട് വിഭജിക്കുന്നിടത്ത്). ബോധ്യപ്പെടുത്താൻ, അച്ചുതണ്ടുകൾ മാനസികമായി മായ്ച്ച് ഒരു ഗ്രാഫ് വിടുക. കാരണം അവിടെയാണ് താൽപര്യം.

ഫംഗ്ഷൻ വർദ്ധിക്കുന്നുഒരു ഇടവേളയിൽ, ഈ ഇടവേളയിലെ ഏതെങ്കിലും രണ്ട് പോയിന്റുകൾക്ക് ബന്ധവുമായി ബന്ധിപ്പിച്ചാൽ, അസമത്വം ശരിയാണ്. അതാണ്, വലിയ മൂല്യംആർഗ്യുമെന്റ് ഫംഗ്ഷന്റെ ഒരു വലിയ മൂല്യവുമായി പൊരുത്തപ്പെടുന്നു, അതിന്റെ ഗ്രാഫ് "താഴെ നിന്ന് മുകളിലേക്ക്" പോകുന്നു. പ്രദർശന പ്രവർത്തനം ഇടവേളയിൽ വളരുന്നു.

അതുപോലെ, പ്രവർത്തനം കുറയുന്നുഒരു ഇടവേളയിൽ, ഒരു നിശ്ചിത ഇടവേളയിലെ ഏതെങ്കിലും രണ്ട് പോയിന്റുകൾക്ക്, അസമത്വം ശരിയാണ്. അതായത്, ആർഗ്യുമെന്റിന്റെ ഒരു വലിയ മൂല്യം ഫംഗ്ഷന്റെ ഒരു ചെറിയ മൂല്യവുമായി പൊരുത്തപ്പെടുന്നു, അതിന്റെ ഗ്രാഫ് "മുകളിൽ നിന്ന് താഴേക്ക്" പോകുന്നു. ഇടവേളകളിൽ നമ്മുടെ പ്രവർത്തനം കുറയുന്നു .

ഒരു ഇടവേളയിൽ ഒരു ഫംഗ്‌ഷൻ കൂടുകയോ കുറയുകയോ ചെയ്‌താൽ, അതിനെ വിളിക്കുന്നു കർശനമായി ഏകതാനമായഈ ഇടവേളയിൽ. എന്താണ് ഏകതാനത? അക്ഷരാർത്ഥത്തിൽ എടുക്കുക - ഏകതാനത.

നിങ്ങൾക്ക് നിർവ്വചിക്കാനും കഴിയും കുറയാത്തത്ഫംഗ്ഷൻ (ആദ്യ നിർവചനത്തിൽ വിശ്രമിച്ച അവസ്ഥ) കൂടാതെ വർദ്ധിക്കാത്തത്ഫംഗ്ഷൻ (രണ്ടാമത്തെ നിർവചനത്തിൽ മൃദുവായ അവസ്ഥ). ഒരു ഇടവേളയിൽ കുറയുകയോ കൂടുകയോ ചെയ്യാത്ത പ്രവർത്തനത്തെ വിളിക്കുന്നു ഏകതാനമായ പ്രവർത്തനംഈ ഇടവേളയിൽ (കണിശമായ ഏകതാനത എന്നത് "ലളിതമായി" ഏകതാനതയുടെ ഒരു പ്രത്യേക സാഹചര്യമാണ്).

പകുതി-ഇടവേളകളിലും സെഗ്‌മെന്റുകളിലും ഉൾപ്പെടെ, ഒരു ഫംഗ്‌ഷന്റെ വർദ്ധനവ്/കുറവ് നിർണ്ണയിക്കുന്നതിനുള്ള മറ്റ് സമീപനങ്ങളും സിദ്ധാന്തം പരിഗണിക്കുന്നു, എന്നാൽ നിങ്ങളുടെ തലയിൽ എണ്ണ-എണ്ണ-എണ്ണ ഒഴിക്കാതിരിക്കാൻ, വർഗ്ഗീയ നിർവചനങ്ങളോടെ തുറന്ന ഇടവേളകളിൽ പ്രവർത്തിക്കാൻ ഞങ്ങൾ സമ്മതിക്കും. - ഇത് കൂടുതൽ വ്യക്തമാണ്, കൂടാതെ നിരവധി പ്രായോഗിക പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിന് ഇത് മതിയാകും.

അങ്ങനെ, എന്റെ ലേഖനങ്ങളിൽ "ഒരു ഫംഗ്‌ഷന്റെ ഏകതാനത" എന്ന വാക്ക് മിക്കവാറും എപ്പോഴും മറഞ്ഞിരിക്കും ഇടവേളകൾകർശനമായ ഏകതാനത(കർശനമായി വർദ്ധിക്കുന്നതോ കർശനമായി കുറയ്ക്കുന്നതോ ആയ പ്രവർത്തനം).

ഒരു പോയിന്റിന്റെ അയൽപക്കം. വിദ്യാർത്ഥികൾ കഴിയുന്നിടത്തെല്ലാം ഓടിപ്പോകുകയും മൂലകളിൽ ഭീതിയോടെ ഒളിക്കുകയും ചെയ്യുന്ന വാക്കുകൾ. ...പോസ്റ്റ് കഴിഞ്ഞാലും Cauchy പരിധികൾഅവർ ഇനി മറഞ്ഞിരിക്കില്ല, പക്ഷേ ചെറുതായി വിറയ്ക്കുന്നു =) വിഷമിക്കേണ്ട, ഇപ്പോൾ ഗണിതശാസ്ത്ര വിശകലനത്തിന്റെ സിദ്ധാന്തങ്ങളുടെ തെളിവുകളൊന്നും ഉണ്ടാകില്ല - നിർവചനങ്ങൾ കൂടുതൽ കർശനമായി രൂപപ്പെടുത്താൻ എനിക്ക് ചുറ്റുപാടുകൾ ആവശ്യമാണ് അങ്ങേയറ്റത്തെ പോയിന്റുകൾ. നമുക്ക് ഓർക്കാം:

ഒരു പോയിന്റിന്റെ അയൽപക്കംഒരു നിശ്ചിത പോയിന്റ് ഉൾക്കൊള്ളുന്ന ഒരു ഇടവേളയെ വിളിക്കുന്നു, സൗകര്യാർത്ഥം ഇടവേള പലപ്പോഴും സമമിതിയാണെന്ന് അനുമാനിക്കപ്പെടുന്നു. ഉദാഹരണത്തിന്, ഒരു പോയിന്റും അതിന്റെ സാധാരണ അയൽപക്കവും:

യഥാർത്ഥത്തിൽ, നിർവചനങ്ങൾ:

പോയിന്റ് വിളിക്കുന്നു കർശനമായ പരമാവധി പോയിന്റ്, എങ്കിൽ നിലവിലുണ്ട്അവളുടെ അയൽപക്കം, എല്ലാവർക്കുംഅതിന്റെ മൂല്യങ്ങൾ, പോയിന്റ് ഒഴികെ, അസമത്വം . ഞങ്ങളുടെ നിർദ്ദിഷ്ട ഉദാഹരണംഇതാണ് കാര്യം.

പോയിന്റ് വിളിക്കുന്നു കർശനമായ മിനിമം പോയിന്റ്, എങ്കിൽ നിലവിലുണ്ട്അവളുടെ അയൽപക്കം, എല്ലാവർക്കുംഅതിന്റെ മൂല്യങ്ങൾ, പോയിന്റ് ഒഴികെ, അസമത്വം . ഡ്രോയിംഗിൽ പോയിന്റ് "a" ഉണ്ട്.

കുറിപ്പ് : അയൽപക്ക സമമിതിയുടെ ആവശ്യകത ഒട്ടും ആവശ്യമില്ല. കൂടാതെ, അത് പ്രധാനമാണ് അസ്തിത്വത്തിന്റെ വസ്തുതനിർദ്ദിഷ്‌ട വ്യവസ്ഥകൾ പാലിക്കുന്ന അയൽപക്കം (ചെറിയതോ സൂക്ഷ്മമായതോ ആകട്ടെ).

പോയിന്റുകൾ വിളിക്കുന്നു കർശനമായി അങ്ങേയറ്റത്തെ പോയിന്റുകൾഅല്ലെങ്കിൽ ലളിതമായി അങ്ങേയറ്റത്തെ പോയിന്റുകൾപ്രവർത്തനങ്ങൾ. അതായത്, പരമാവധി പോയിന്റുകൾക്കും കുറഞ്ഞ പോയിന്റുകൾക്കുമുള്ള സാമാന്യവൽക്കരിച്ച പദമാണിത്.

"തീവ്രം" എന്ന വാക്ക് എങ്ങനെ മനസ്സിലാക്കാം? അതെ, ഏകതാനത പോലെ നേരിട്ട്. റോളർ കോസ്റ്ററുകളുടെ അങ്ങേയറ്റം പോയിന്റുകൾ.

ഏകതാനതയുടെ കാര്യത്തിലെന്നപോലെ, അയഞ്ഞ പോസ്റ്റുലേറ്റുകൾ നിലവിലുണ്ട്, അവ സിദ്ധാന്തത്തിൽ കൂടുതൽ സാധാരണമാണ് (തീർച്ചയായും, പരിഗണിക്കപ്പെടുന്ന കർശനമായ കേസുകൾ ഇതിൽ ഉൾപ്പെടുന്നു!):

പോയിന്റ് വിളിക്കുന്നു പരമാവധി പോയിന്റ്, എങ്കിൽ നിലവിലുണ്ട്അതിന്റെ ചുറ്റുപാടുകൾ അങ്ങനെയാണ് എല്ലാവർക്കും
പോയിന്റ് വിളിക്കുന്നു മിനിമം പോയിന്റ്, എങ്കിൽ നിലവിലുണ്ട്അതിന്റെ ചുറ്റുപാടുകൾ അങ്ങനെയാണ് എല്ലാവർക്കുംഈ അയൽപക്കത്തിന്റെ മൂല്യങ്ങൾ, അസമത്വം നിലനിർത്തുന്നു.

അവസാന രണ്ട് നിർവചനങ്ങൾ അനുസരിച്ച്, ഒരു സ്ഥിരമായ ഫംഗ്‌ഷന്റെ (അല്ലെങ്കിൽ ഒരു ഫംഗ്‌ഷന്റെ “ഫ്ലാറ്റ് സെക്ഷൻ”) ഏതെങ്കിലും പോയിന്റ് പരമാവധി, മിനിമം പോയിന്റായി കണക്കാക്കുന്നു. പ്രവർത്തനം, വഴിയിൽ, വർദ്ധിക്കാത്തതും കുറയാത്തതുമാണ്, അതായത്, ഏകതാനമാണ്. എന്നിരുന്നാലും, ഞങ്ങൾ ഈ പരിഗണനകൾ സൈദ്ധാന്തികർക്ക് വിട്ടുകൊടുക്കും, കാരണം പ്രായോഗികമായി ഞങ്ങൾ എല്ലായ്പ്പോഴും പരമ്പരാഗത "കുന്നുകൾ", "പൊള്ളകൾ" (ഡ്രോയിംഗ് കാണുക) ഒരു അതുല്യമായ "കുന്നിലെ രാജാവ്" അല്ലെങ്കിൽ "ചതുപ്പിന്റെ രാജകുമാരി" എന്നിവയെക്കുറിച്ച് ചിന്തിക്കുന്നു. ഒരു വൈവിധ്യമെന്ന നിലയിൽ, അത് സംഭവിക്കുന്നു നുറുങ്ങ്, മുകളിലേക്കോ താഴേയ്‌ക്കോ നയിക്കപ്പെടുന്നു, ഉദാഹരണത്തിന്, പോയിന്റിലെ ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞത്.

ഓ, റോയൽറ്റിയെക്കുറിച്ച് സംസാരിക്കുന്നു:
- അർത്ഥം വിളിക്കുന്നു പരമാവധിപ്രവർത്തനങ്ങൾ;
- അർത്ഥം വിളിക്കുന്നു ഏറ്റവും കുറഞ്ഞത്പ്രവർത്തനങ്ങൾ.

പൊതുവായ പേര് - അങ്ങേയറ്റംപ്രവർത്തനങ്ങൾ.

ദയവായി നിങ്ങളുടെ വാക്കുകൾ ശ്രദ്ധിക്കുക!

എക്സ്ട്രീം പോയിന്റുകൾ- ഇവ "എക്സ്" മൂല്യങ്ങളാണ്.
അതിരുകൾ- "ഗെയിം" അർത്ഥങ്ങൾ.

! കുറിപ്പ് : ചിലപ്പോൾ ലിസ്‌റ്റ് ചെയ്‌ത പദങ്ങൾ ഫംഗ്‌ഷന്റെ ഗ്രാഫിൽ നേരിട്ട് കിടക്കുന്ന "X-Y" പോയിന്റുകളെ സൂചിപ്പിക്കുന്നു.

ഒരു ഫംഗ്‌ഷന് എത്ര എക്സ്ട്രീമകൾ ഉണ്ടായിരിക്കും?

ഒന്നുമില്ല, 1, 2, 3, ... തുടങ്ങിയവ. അനന്തതയിലേയ്ക്ക്. ഉദാഹരണത്തിന്, സൈനിന് അനന്തമായ മിനിമയും മാക്സിമയും ഉണ്ട്.

പ്രധാനം!"പരമാവധി പ്രവർത്തനക്ഷമത" എന്ന പദം സമാനമല്ല"ഒരു ഫംഗ്ഷന്റെ പരമാവധി മൂല്യം" എന്ന പദം. ഒരു പ്രാദേശിക അയൽപക്കത്തിൽ മാത്രമേ മൂല്യം പരമാവധി ആണെന്ന് ശ്രദ്ധിക്കുന്നത് എളുപ്പമാണ്, മുകളിൽ ഇടതുവശത്ത് "തണുത്ത സഖാക്കൾ" ഉണ്ട്. അതുപോലെ, "ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ മൂല്യം" എന്നത് "ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ മൂല്യം" എന്നതിന് തുല്യമല്ല, കൂടാതെ ഡ്രോയിംഗിൽ ഒരു നിശ്ചിത പ്രദേശത്ത് മാത്രമേ മൂല്യം ഏറ്റവും കുറവാണെന്ന് നമ്മൾ കാണുന്നത്. ഇക്കാര്യത്തിൽ, എക്സ്ട്രീം പോയിന്റുകൾ എന്നും വിളിക്കപ്പെടുന്നു പ്രാദേശിക എക്സ്ട്രീം പോയിന്റുകൾ, തീവ്രവും - പ്രാദേശിക അതിരുകൾ. അവർ സമീപത്ത് നടക്കുകയും അലഞ്ഞുതിരിയുകയും ചെയ്യുന്നു ആഗോളസഹോദരങ്ങളെ. അതിനാൽ, ഏത് പരവലയവും അതിന്റെ ശിഖരത്തിലാണ് ആഗോള മിനിമംഅഥവാ ആഗോള പരമാവധി. കൂടാതെ, ഞാൻ അതിരുകടന്ന തരങ്ങൾ തമ്മിൽ വേർതിരിക്കില്ല, കൂടാതെ വിശദീകരണം പൊതുവായ വിദ്യാഭ്യാസ ആവശ്യങ്ങൾക്കായി കൂടുതൽ ശബ്ദമുയർത്തുന്നു - "ലോക്കൽ" / "ഗ്ലോബൽ" എന്ന അധിക നാമവിശേഷണങ്ങൾ നിങ്ങളെ ആശ്ചര്യപ്പെടുത്തരുത്.

നമുക്ക് നമ്മുടെ സംഗ്രഹിക്കാം ചെറിയ ഉല്ലാസയാത്രഒരു ടെസ്റ്റ് ഷോട്ട് ഉപയോഗിച്ച് സിദ്ധാന്തത്തിലേക്ക്: "ഫംഗ്ഷന്റെ മോണോടോണിസിറ്റി ഇടവേളകളും എക്സ്ട്രീം പോയിന്റുകളും കണ്ടെത്തുക" എന്ന ടാസ്ക് എന്താണ് അർത്ഥമാക്കുന്നത്?

പദാവലി നിങ്ങളെ കണ്ടെത്താൻ പ്രോത്സാഹിപ്പിക്കുന്നു:

- വർദ്ധിച്ചുവരുന്ന / കുറയുന്ന പ്രവർത്തനത്തിന്റെ ഇടവേളകൾ (കുറയാത്തതും വർദ്ധിക്കാത്തതും വളരെ കുറച്ച് തവണ പ്രത്യക്ഷപ്പെടുന്നു);

- പരമാവധി കൂടാതെ/അല്ലെങ്കിൽ ഏറ്റവും കുറഞ്ഞ പോയിന്റുകൾ (എന്തെങ്കിലും ഉണ്ടെങ്കിൽ). ശരി, പരാജയം ഒഴിവാക്കാൻ, മിനിമം / മാക്സിമങ്ങൾ സ്വയം കണ്ടെത്തുന്നതാണ് നല്ലത് ;-)

ഇതെല്ലാം എങ്ങനെ നിർണ്ണയിക്കും?ഡെറിവേറ്റീവ് ഫംഗ്ഷൻ ഉപയോഗിക്കുന്നു!

കൂടുന്നതിന്റെയും കുറയുന്നതിന്റെയും ഇടവേളകൾ എങ്ങനെ കണ്ടെത്താം
ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീം പോയിന്റുകളും എക്‌സ്ട്രീമയും?

പല നിയമങ്ങളും, വാസ്തവത്തിൽ, ഇതിനകം അറിയുകയും മനസ്സിലാക്കുകയും ചെയ്തിട്ടുണ്ട് ഒരു ഡെറിവേറ്റീവിന്റെ അർത്ഥത്തെക്കുറിച്ചുള്ള പാഠം.

ടാൻജന്റ് ഡെറിവേറ്റീവ് പ്രവർത്തനം ഉടനീളം വർദ്ധിച്ചുകൊണ്ടിരിക്കുന്നു എന്ന സന്തോഷകരമായ വാർത്ത കൊണ്ടുവരുന്നു നിർവചനത്തിന്റെ ഡൊമെയ്ൻ.

കോട്ടാൻജെന്റും അതിന്റെ ഡെറിവേറ്റീവും ഉപയോഗിച്ച് സ്ഥിതി നേരെ വിപരീതമാണ്.

ഇടവേളയിൽ ആർക്സൈൻ വർദ്ധിക്കുന്നു - ഇവിടെയുള്ള ഡെറിവേറ്റീവ് പോസിറ്റീവ് ആണ്: .
ഫംഗ്ഷൻ നിർവചിക്കുമ്പോൾ, എന്നാൽ വ്യത്യാസമില്ല. എന്നിരുന്നാലും, നിർണായക ഘട്ടത്തിൽ ഒരു വലംകൈയ്യൻ ഡെറിവേറ്റീവും വലംകൈയൻ ടാൻജെന്റും ഉണ്ട്, മറ്റേ അറ്റത്ത് അവരുടെ ഇടതുകൈയ്യൻ എതിരാളികളുമുണ്ട്.

ആർക്ക് കോസൈനിനും അതിന്റെ ഡെറിവേറ്റീവിനും സമാനമായ ന്യായവാദം നടത്തുന്നത് നിങ്ങൾക്ക് ബുദ്ധിമുട്ടുള്ള കാര്യമല്ലെന്ന് ഞാൻ കരുതുന്നു.

മുകളിലുള്ള എല്ലാ കേസുകളും, അവയിൽ പലതും പട്ടിക ഡെറിവേറ്റീവുകൾ, ഞാൻ നിങ്ങളെ ഓർമ്മിപ്പിക്കുന്നു, നേരിട്ട് പിന്തുടരുക ഡെറിവേറ്റീവ് നിർവചനങ്ങൾ.

ഒരു ഫംഗ്‌ഷൻ അതിന്റെ ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് പര്യവേക്ഷണം ചെയ്യുന്നത് എന്തുകൊണ്ട്?

ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫ് എങ്ങനെയുണ്ടെന്ന് നന്നായി മനസ്സിലാക്കാൻ: അത് "താഴെ മുകളിലേക്ക്" പോകുന്നിടത്ത്, "മുകളിൽ നിന്ന് താഴേക്ക്", എവിടെയാണ് അത് മിനിമം, മാക്സിമം (എല്ലാം എത്തിയാൽ). എല്ലാ ഫംഗ്‌ഷനുകളും അത്ര ലളിതമല്ല - മിക്ക കേസുകളിലും ഒരു പ്രത്യേക ഫംഗ്‌ഷന്റെ ഗ്രാഫിനെക്കുറിച്ച് ഞങ്ങൾക്ക് യാതൊരു ധാരണയുമില്ല.

കൂടുതൽ അർത്ഥവത്തായ ഉദാഹരണങ്ങളിലേക്ക് നീങ്ങാനും പരിഗണിക്കാനുമുള്ള സമയമാണിത് ഒരു ഫംഗ്‌ഷന്റെ ഏകതാനതയുടെയും തീവ്രതയുടെയും ഇടവേളകൾ കണ്ടെത്തുന്നതിനുള്ള അൽഗോരിതം:

ഉദാഹരണം 1

പ്രവർത്തനത്തിന്റെ വർദ്ധനവ്/കുറവ്, തീവ്രത എന്നിവയുടെ ഇടവേളകൾ കണ്ടെത്തുക

പരിഹാരം:

1) കണ്ടെത്തുക എന്നതാണ് ആദ്യപടി ഒരു ഫംഗ്ഷന്റെ ഡൊമെയ്ൻ, കൂടാതെ ബ്രേക്ക് പോയിന്റുകളും (അവ നിലവിലുണ്ടെങ്കിൽ) ശ്രദ്ധിക്കുക. IN ഈ സാഹചര്യത്തിൽഫംഗ്ഷൻ മുഴുവൻ നമ്പർ ലൈനിലും തുടർച്ചയായി നടക്കുന്നു, ഈ പ്രവർത്തനം ഒരു പരിധി വരെ ഔപചാരികമാണ്. എന്നാൽ പല കേസുകളിലും, ഗുരുതരമായ വികാരങ്ങൾ ഇവിടെ ജ്വലിക്കുന്നു, അതിനാൽ നമുക്ക് ഖണ്ഡികയെ അവഗണന കൂടാതെ പരിഗണിക്കാം.

2) അൽഗോരിതത്തിന്റെ രണ്ടാമത്തെ പോയിന്റ് കാരണം

ഒരു തീവ്രതയ്ക്ക് ആവശ്യമായ വ്യവസ്ഥ:

ഒരു ബിന്ദുവിൽ ഒരു എക്സ്ട്രീം ഉണ്ടെങ്കിൽ, ഒന്നുകിൽ മൂല്യം നിലവിലില്ല.

അവസാനം ആശയക്കുഴപ്പത്തിലാണോ? "മോഡുലസ് x" ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം .

വ്യവസ്ഥ ആവശ്യമാണ്, പക്ഷേ പോരാ, സംഭാഷണം എല്ലായ്പ്പോഴും ശരിയല്ല. അതിനാൽ, പോയിന്റിൽ ഫംഗ്‌ഷൻ പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞതിലെത്തുന്നത് തുല്യതയിൽ നിന്ന് ഇതുവരെ പിന്തുടരുന്നില്ല. ക്ലാസിക് ഉദാഹരണംമുകളിൽ ഇതിനകം ഹൈലൈറ്റ് ചെയ്തിട്ടുണ്ട് - ഇതൊരു ക്യൂബിക് പരവലയവും അതിന്റെ നിർണായക പോയിന്റുമാണ്.

അത് എന്തായാലും, ഒരു തീവ്രതയ്ക്ക് ആവശ്യമായ വ്യവസ്ഥ സംശയാസ്പദമായ പോയിന്റുകൾ കണ്ടെത്തേണ്ടതിന്റെ ആവശ്യകതയെ സൂചിപ്പിക്കുന്നു. ഇത് ചെയ്യുന്നതിന്, ഡെറിവേറ്റീവ് കണ്ടെത്തി സമവാക്യം പരിഹരിക്കുക:

ആദ്യ ലേഖനത്തിന്റെ തുടക്കത്തിൽ ഫംഗ്ഷൻ ഗ്രാഫുകളെ കുറിച്ച്ഒരു ഉദാഹരണം ഉപയോഗിച്ച് ഒരു പരവലയം എങ്ങനെ വേഗത്തിൽ നിർമ്മിക്കാമെന്ന് ഞാൻ നിങ്ങളോട് പറഞ്ഞു : “...ഞങ്ങൾ ആദ്യത്തെ ഡെറിവേറ്റീവ് എടുത്ത് അതിനെ പൂജ്യത്തിന് തുല്യമാക്കുന്നു: ...അതിനാൽ, ഞങ്ങളുടെ സമവാക്യത്തിനുള്ള പരിഹാരം: - ഈ ഘട്ടത്തിലാണ് പരവലയത്തിന്റെ ശീർഷകം സ്ഥിതിചെയ്യുന്നത് ...”. ഇപ്പോൾ, ഞാൻ കരുതുന്നു, പരവലയത്തിന്റെ ശീർഷകം കൃത്യമായി ഈ ഘട്ടത്തിൽ സ്ഥിതിചെയ്യുന്നത് എന്തുകൊണ്ടാണെന്ന് എല്ലാവർക്കും മനസ്സിലാകും =) പൊതുവേ, നമ്മൾ ഇവിടെ സമാനമായ ഒരു ഉദാഹരണം ഉപയോഗിച്ച് ആരംഭിക്കണം, പക്ഷേ ഇത് വളരെ ലളിതമാണ് (ഒരു ചായകുടിക്ക് പോലും). കൂടാതെ, പാഠത്തിന്റെ അവസാനത്തിൽ ഒരു അനലോഗ് ഉണ്ട് ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ്. അതിനാൽ, നമുക്ക് ബിരുദം വർദ്ധിപ്പിക്കാം:

ഉദാഹരണം 2

ഫംഗ്‌ഷന്റെ ഏകതാനതയുടെയും തീവ്രതയുടെയും ഇടവേളകൾ കണ്ടെത്തുക

ഇത് ഒരു ഉദാഹരണമാണ് സ്വതന്ത്ര തീരുമാനം. സമ്പൂർണ്ണ പരിഹാരംപാഠത്തിന്റെ അവസാനത്തിൽ ടാസ്ക്കിന്റെ ഏകദേശ അന്തിമ മാതൃകയും.

ഫ്രാക്ഷണൽ-റേഷണൽ ഫംഗ്ഷനുകളുമായുള്ള കൂടിക്കാഴ്ചയുടെ ദീർഘകാലമായി കാത്തിരുന്ന നിമിഷം വന്നിരിക്കുന്നു:

ഉദാഹരണം 3

ആദ്യത്തെ ഡെറിവേറ്റീവ് ഉപയോഗിച്ച് ഒരു ഫംഗ്ഷൻ പര്യവേക്ഷണം ചെയ്യുക

ഒരേ ടാസ്‌ക് എത്രമാത്രം വേരിയബിളായി പരിഷ്‌കരിക്കാനാകുമെന്ന് ശ്രദ്ധിക്കുക.

പരിഹാരം:

1) ഫംഗ്‌ഷൻ പോയിന്റുകളിൽ അനന്തമായ തടസ്സങ്ങൾ നേരിടുന്നു.

2) നിർണായക പോയിന്റുകൾ ഞങ്ങൾ കണ്ടെത്തുന്നു. നമുക്ക് ആദ്യത്തെ ഡെറിവേറ്റീവ് കണ്ടെത്തി അതിനെ പൂജ്യത്തിന് തുല്യമാക്കാം:

നമുക്ക് സമവാക്യം പരിഹരിക്കാം. ഒരു അംശം പൂജ്യമാകുമ്പോൾ അത് പൂജ്യമാണ്:

അങ്ങനെ, നമുക്ക് മൂന്ന് നിർണായക പോയിന്റുകൾ ലഭിക്കും:

3) നമ്പർ ലൈനിൽ കണ്ടെത്തിയ എല്ലാ പോയിന്റുകളും ഞങ്ങൾ പ്ലോട്ട് ചെയ്യുന്നു ഇടവേള രീതിഡെറിവേറ്റീവിന്റെ അടയാളങ്ങൾ ഞങ്ങൾ നിർവ്വചിക്കുന്നു:

നിങ്ങൾ ഇടവേളയിൽ കുറച്ച് പോയിന്റ് എടുത്ത് അതിൽ ഡെറിവേറ്റീവിന്റെ മൂല്യം കണക്കാക്കേണ്ടതുണ്ടെന്ന് ഞാൻ നിങ്ങളെ ഓർമ്മിപ്പിക്കുന്നു അതിന്റെ അടയാളം നിർണ്ണയിക്കുക. കണക്കാക്കാൻ പോലും ഇത് കൂടുതൽ ലാഭകരമാണ്, പക്ഷേ വാക്കാലുള്ള "കണക്കിന്". ഉദാഹരണത്തിന്, ഇടവേളയിൽ ഉൾപ്പെടുന്ന ഒരു പോയിന്റ് എടുത്ത് പകരം വയ്ക്കൽ നടത്താം: .

രണ്ട് “പ്ലസുകളും” ഒരു “മൈനസും” ഒരു “മൈനസ്” നൽകുന്നു, അതിനാൽ, ഡെറിവേറ്റീവ് മുഴുവൻ ഇടവേളയിലും നെഗറ്റീവ് ആണെന്നാണ് അർത്ഥമാക്കുന്നത്.

നിങ്ങൾ മനസ്സിലാക്കുന്നതുപോലെ, ഓരോ ആറ് ഇടവേളകളിലും പ്രവർത്തനം നടത്തേണ്ടതുണ്ട്. വഴിയിൽ, ന്യൂമറേറ്റർ ഘടകവും ഡിനോമിനേറ്ററും ഏത് ഇടവേളയിലെയും ഏത് പോയിന്റിനും കർശനമായി പോസിറ്റീവ് ആണെന്ന് ശ്രദ്ധിക്കുക, ഇത് ചുമതലയെ വളരെയധികം ലളിതമാക്കുന്നു.

അതിനാൽ, ഡെറിവേറ്റീവ് ഞങ്ങളോട് പറഞ്ഞു, ഫംഗ്ഷൻ സ്വയം വർദ്ധിക്കുന്നു കൂടാതെ കുറയുന്നു. ജോയിൻ ഐക്കൺ ഉപയോഗിച്ച് ഒരേ തരത്തിലുള്ള ഇടവേളകൾ ബന്ധിപ്പിക്കുന്നത് സൗകര്യപ്രദമാണ്.

ഈ ഘട്ടത്തിൽ, പ്രവർത്തനം അതിന്റെ പരമാവധിയിലെത്തുന്നു:
ഈ ഘട്ടത്തിൽ ഫംഗ്ഷൻ ഏറ്റവും കുറഞ്ഞത് എത്തുന്നു:

എന്തുകൊണ്ടാണ് നിങ്ങൾ രണ്ടാമത്തെ മൂല്യം വീണ്ടും കണക്കാക്കേണ്ടതില്ലെന്ന് ചിന്തിക്കുക ;-)

ഒരു പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ, ഡെറിവേറ്റീവ് ചിഹ്നം മാറില്ല, അതിനാൽ ഫംഗ്‌ഷനിൽ എക്‌സ്‌ട്രീമമില്ല - അത് കുറയുകയും കുറയുകയും ചെയ്തു.

! നമുക്ക് ആവർത്തിക്കാം പ്രധാനപ്പെട്ട പോയിന്റ് : പോയിന്റുകൾ നിർണായകമായി കണക്കാക്കില്ല - അവയിൽ ഒരു ഫംഗ്ഷൻ അടങ്ങിയിരിക്കുന്നു നിർണയിക്കപ്പെട്ടിട്ടില്ല. അതനുസരിച്ച്, ഇവിടെ തത്വത്തിൽ അങ്ങേയറ്റം ഉണ്ടാകാൻ പാടില്ല(ഡെറിവേറ്റീവ് ചിഹ്നം മാറിയാലും).

ഉത്തരം: പ്രവർത്തനം വർദ്ധിപ്പിക്കുന്നു ഫംഗ്‌ഷന്റെ പരമാവധി എത്തിയ ഘട്ടത്തിൽ കുറയുന്നു: , ഒപ്പം പോയിന്റിൽ - ഏറ്റവും കുറഞ്ഞത്: .

മോണോടോണിസിറ്റി ഇടവേളകളെക്കുറിച്ചും തീവ്രതയെക്കുറിച്ചും ഉള്ള അറിവ്, ഒപ്പം സ്ഥാപിതമായി രോഗലക്ഷണങ്ങൾഇതിനകം വളരെ നല്ല ആശയം നൽകുന്നു രൂപംഫംഗ്ഷൻ ഗ്രാഫിക്സ്. ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫിന് രണ്ട് ലംബമായ അസിംപ്റ്റോട്ടുകളും ഒരു ചരിഞ്ഞ അസിംപ്റ്റോട്ടും ഉണ്ടെന്ന് ശരാശരി പരിശീലനമുള്ള ഒരു വ്യക്തിക്ക് വാക്കാലുള്ള നിർണ്ണയിക്കാൻ കഴിയും. ഇതാ നമ്മുടെ നായകൻ:

പഠനത്തിന്റെ ഫലങ്ങൾ ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫുമായി ബന്ധപ്പെടുത്താൻ ഒരിക്കൽ കൂടി ശ്രമിക്കുക.
നിർണായക ഘട്ടത്തിൽ തീവ്രതയില്ല, പക്ഷേ ഉണ്ട് ഗ്രാഫ് ഇൻഫ്ലക്ഷൻ(ചട്ടം പോലെ, സമാനമായ കേസുകളിൽ ഇത് സംഭവിക്കുന്നു).

ഉദാഹരണം 4

പ്രവർത്തനത്തിന്റെ തീവ്രത കണ്ടെത്തുക

ഉദാഹരണം 5

പ്രവർത്തനത്തിന്റെ ഏകതാനത ഇടവേളകൾ, മാക്സിമ, മിനിമ എന്നിവ കണ്ടെത്തുക

…ഇന്ന് ഏതാണ്ട് ഒരുതരം "എക്സ് ഇൻ എ ക്യൂബ്" അവധി പോലെയാണ്....
സോ, ഗാലറിയിൽ ആരാണ് ഇതിന് കുടിക്കാൻ വാഗ്ദാനം ചെയ്തത്? =)

ഓരോ ടാസ്ക്കിനും അതിന്റേതായ കാര്യമായ സൂക്ഷ്മതകളും സാങ്കേതിക സൂക്ഷ്മതകളും ഉണ്ട്, അവ പാഠത്തിന്റെ അവസാനം അഭിപ്രായപ്പെടുന്നു.

തുടർച്ചയായ പ്രവർത്തനത്തിന്റെ ഗ്രാഫ് പരിഗണിക്കുക y=f(x)ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്നു.

ഒരു പോയിന്റിലെ പ്രവർത്തന മൂല്യം x 1 ഇടത്തോട്ടും വലത്തോട്ടും ഉള്ള എല്ലാ അയൽ പോയിന്റുകളിലെയും ഫംഗ്‌ഷൻ മൂല്യങ്ങളേക്കാൾ വലുതായിരിക്കും x 1 . ഈ സാഹചര്യത്തിൽ, പ്രവർത്തനത്തിന് പോയിന്റ് ഉണ്ടെന്ന് ഞങ്ങൾ പറയുന്നു xപരമാവധി 1. പോയിന്റിൽ xഫംഗ്ഷൻ 3 വ്യക്തമായും പരമാവധി ഉണ്ട്. ഞങ്ങൾ പോയിന്റ് പരിഗണിക്കുകയാണെങ്കിൽ x 2, അപ്പോൾ അതിലെ ഫംഗ്ഷൻ മൂല്യം എല്ലാ അയൽ മൂല്യങ്ങളേക്കാളും കുറവാണ്. ഈ സാഹചര്യത്തിൽ, പ്രവർത്തനത്തിന് പോയിന്റ് ഉണ്ടെന്ന് ഞങ്ങൾ പറയുന്നു x 2 കുറഞ്ഞത്. അതുപോലെ പോയിന്റിനും x 4 .

ഫംഗ്ഷൻ y=f(x)പോയിന്റിൽ x 0 ഉണ്ട് പരമാവധി, ഈ പോയിന്റിലെ ഫംഗ്‌ഷന്റെ മൂല്യം പോയിന്റ് അടങ്ങിയിരിക്കുന്ന ചില ഇടവേളകളിലെ എല്ലാ പോയിന്റുകളിലും അതിന്റെ മൂല്യങ്ങളേക്കാൾ കൂടുതലാണെങ്കിൽ x 0, അതായത്. ഒരു പോയിന്റിന്റെ അത്തരമൊരു സമീപസ്ഥലം ഉണ്ടെങ്കിൽ x 0, ഇത് എല്ലാവർക്കും വേണ്ടിയുള്ളതാണ് x≠x 0 , ഈ അയൽപക്കത്തിൽ പെടുന്നു, അസമത്വം നിലനിൽക്കുന്നു f(x)<f(x 0 ) .

ഫംഗ്ഷൻ y=f(x)അതിനുണ്ട് ഏറ്റവും കുറഞ്ഞത്പോയിന്റിൽ x 0 , ഒരു പോയിന്റിന്റെ അത്തരമൊരു സമീപസ്ഥലം ഉണ്ടെങ്കിൽ x 0 , അത് എല്ലാവർക്കും വേണ്ടിയുള്ളതാണ് x≠x 0 ഈ അയൽപക്കത്തിൽ പെട്ടതാണ്, അസമത്വം നിലനിർത്തുന്നു f(x)>f(x 0.

ഫംഗ്‌ഷൻ അതിന്റെ പരമാവധിയിലും കുറഞ്ഞതിലും എത്തുന്ന പോയിന്റുകളെ എക്‌സ്‌ട്രീം പോയിന്റുകൾ എന്നും ഈ പോയിന്റുകളിലെ ഫംഗ്‌ഷന്റെ മൂല്യങ്ങളെ ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീമ എന്നും വിളിക്കുന്നു.

ഒരു സെഗ്‌മെന്റിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്‌ഷന് പരിഗണനയിലുള്ള സെഗ്‌മെന്റിനുള്ളിൽ അടങ്ങിയിരിക്കുന്ന പോയിന്റുകളിൽ മാത്രമേ അതിന്റെ പരമാവധിയിലും കുറഞ്ഞതിലും എത്താൻ കഴിയൂ എന്ന വസ്തുത നമുക്ക് ശ്രദ്ധിക്കാം.

ഒരു ഫംഗ്‌ഷന് ഒരു പോയിന്റിൽ പരമാവധി ഉണ്ടെങ്കിൽ, ആ ഘട്ടത്തിൽ ഫംഗ്‌ഷന് നിർവചനത്തിന്റെ മുഴുവൻ ഡൊമെയ്‌നിലും ഏറ്റവും വലിയ മൂല്യമുണ്ടെന്ന് ഇതിനർത്ഥമില്ല. മുകളിൽ ചർച്ച ചെയ്ത ചിത്രത്തിൽ, പോയിന്റിലെ പ്രവർത്തനം xഫംഗ്‌ഷൻ മൂല്യങ്ങൾ പോയിന്റിനേക്കാൾ വലുതായ പോയിന്റുകൾ ഉണ്ടെങ്കിലും 1 ന് പരമാവധി ഉണ്ട് x 1 . പ്രത്യേകിച്ച്, എഫ്(x 1) < എഫ്(x 4) അതായത് ഒരു ഫംഗ്‌ഷന്റെ മിനിമം പരമാവധി എന്നതിനേക്കാൾ കൂടുതലാണ്. മാക്സിമം എന്നതിന്റെ നിർവചനത്തിൽ നിന്ന് ഇത് ഏറ്റവും കൂടുതൽ ആണെന്ന് മാത്രം വലിയ പ്രാധാന്യംപരമാവധി പോയിന്റിനോട് അടുത്ത് നിൽക്കുന്ന പോയിന്റുകളിൽ പ്രവർത്തിക്കുന്നു.

സിദ്ധാന്തം 1. (ഒരു തീവ്രതയുടെ നിലനിൽപ്പിന് ആവശ്യമായ വ്യവസ്ഥ.)വ്യതിരിക്തമായ പ്രവർത്തനമാണെങ്കിൽ y=f(x)പോയിന്റിൽ ഉണ്ട് x= x 0 എക്സ്ട്രീം, ഈ ഘട്ടത്തിൽ അതിന്റെ ഡെറിവേറ്റീവ് പൂജ്യമായി മാറുന്നു.

തെളിവ്. വ്യക്തതയ്ക്കായി, പോയിന്റിൽ വരട്ടെ x 0 ഫംഗ്‌ഷന് പരമാവധി ഉണ്ട്. തുടർന്ന്, മതിയായ ചെറിയ വർദ്ധനവിന് Δ xനമുക്ക് ഉണ്ട് f(x 0 + Δ x) 0 ) , അതായത്. പക്ഷേ എന്നിട്ട്

ഈ അസമത്വങ്ങളിൽ Δ എന്ന പരിധി വരെ കടന്നുപോകുന്നു x→ 0 കൂടാതെ ഡെറിവേറ്റീവ് എന്നത് കണക്കിലെടുക്കുന്നു എഫ് "(x 0) നിലവിലുണ്ട്, അതിനാൽ ഇടതുവശത്തെ പരിധി എങ്ങനെ Δ എന്നതിനെ ആശ്രയിക്കുന്നില്ല x→ 0, നമുക്ക് ലഭിക്കുന്നത്: Δ-ൽ x → 0 – 0 f"(x 0) Δ-ൽ ≥ 0 a x → 0 + 0 f"(x 0) ≤ 0. മുതൽ f"(x 0) ഒരു സംഖ്യയെ നിർവചിക്കുന്നു, ഈ രണ്ട് അസമത്വങ്ങളും പൊരുത്തപ്പെടുന്നെങ്കിൽ മാത്രം f"(x 0) = 0.

ഡെറിവേറ്റീവ് പൂജ്യമാകുന്ന ആർഗ്യുമെന്റിന്റെ മൂല്യങ്ങളിൽ മാത്രമേ പരമാവധി, കുറഞ്ഞ പോയിന്റുകൾ ഉണ്ടാകൂ എന്ന് തെളിയിക്കപ്പെട്ട സിദ്ധാന്തം പറയുന്നു.

ഒരു ഫംഗ്‌ഷന് ഒരു നിശ്ചിത സെഗ്‌മെന്റിന്റെ എല്ലാ പോയിന്റുകളിലും ഒരു ഡെറിവേറ്റീവ് ഉള്ളപ്പോൾ ഞങ്ങൾ കേസ് പരിഗണിച്ചു. ഡെറിവേറ്റീവ് നിലവിലില്ലാത്ത സന്ദർഭങ്ങളിൽ എന്താണ് സ്ഥിതി? ഉദാഹരണങ്ങൾ നോക്കാം.

ഉദാഹരണങ്ങൾ.

1. വൈ=|x|.

   പ്രവർത്തനത്തിന് പോയിന്റിൽ ഡെറിവേറ്റീവ് ഇല്ല x=0 (ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന്റെ ഗ്രാഫിന് നിർവചിക്കപ്പെട്ട ഒരു ടാൻജെന്റ് ഇല്ല), എന്നാൽ ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന് ഒരു മിനിമം ഉണ്ട്, കാരണം വൈ(0)=0, കൂടാതെ എല്ലാവർക്കും x≠ 0വൈ > 0.



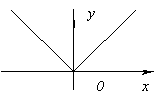
ഫംഗ്‌ഷനിൽ ഡെറിവേറ്റീവ് ഇല്ല x=0, അത് അനന്തതയിലേക്ക് പോകുന്നതിനാൽ x=0. എന്നാൽ ഈ ഘട്ടത്തിൽ പ്രവർത്തനത്തിന് പരമാവധി ഉണ്ട്.



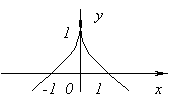
ഫംഗ്‌ഷനിൽ ഡെറിവേറ്റീവ് ഇല്ല x=0, മുതൽ ചെയ്തത് x→0. ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന് പരമാവധി അല്ലെങ്കിൽ മിനിമം ഇല്ല. ശരിക്കും, f(x)=0 ഒപ്പം x<0f(x)<0, а при x>0f(x)>0.



അങ്ങനെ, നൽകിയിരിക്കുന്ന ഉദാഹരണങ്ങളിൽ നിന്നും രൂപപ്പെടുത്തിയ സിദ്ധാന്തത്തിൽ നിന്നും, ഒരു ഫംഗ്ഷന് രണ്ട് സന്ദർഭങ്ങളിൽ മാത്രമേ ഒരു എക്സ്ട്രീം ഉണ്ടാകൂ എന്ന് വ്യക്തമാണ്: 1) ഡെറിവേറ്റീവ് നിലനിൽക്കുന്നതും പൂജ്യത്തിന് തുല്യവുമായ പോയിന്റുകളിൽ; 2) ഡെറിവേറ്റീവ് നിലവിലില്ലാത്ത സ്ഥലത്ത്.

എന്നിരുന്നാലും, ചില ഘട്ടങ്ങളിൽ എങ്കിൽ x 0 അത് ഞങ്ങൾക്കറിയാം f "(x 0 ) =0, അപ്പോൾ ആ പോയിന്റിൽ നിന്ന് ഒരാൾക്ക് നിഗമനം ചെയ്യാൻ കഴിയില്ല x 0 ഫങ്ഷന് ഒരു എക്സ്ട്രീം ഉണ്ട്.

ഉദാഹരണത്തിന്. .



എന്നാൽ കാലഘട്ടം x=0 ഒരു എക്സ്ട്രീം പോയിന്റല്ല, കാരണം ഈ പോയിന്റിന്റെ ഇടതുവശത്ത് ഫംഗ്ഷൻ മൂല്യങ്ങൾ അക്ഷത്തിന് താഴെയാണ് സ്ഥിതി ചെയ്യുന്നത് കാള, മുകളിൽ വലതുവശത്ത്.

ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് അപ്രത്യക്ഷമാകുന്നതോ നിലവിലില്ലാത്തതോ ആയ ഒരു ഫംഗ്‌ഷന്റെ ഡൊമെയ്‌നിൽ നിന്നുള്ള ഒരു ആർഗ്യുമെന്റിന്റെ മൂല്യങ്ങളെ വിളിക്കുന്നു നിർണായക പോയിന്റുകൾ.




മേൽപ്പറഞ്ഞവയിൽ നിന്ന്, ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം പോയിന്റുകൾ നിർണ്ണായക പോയിന്റുകളിൽ ഉൾപ്പെടുന്നു, എന്നിരുന്നാലും, എല്ലാ നിർണായക പോയിന്റുകളും ഒരു എക്‌സ്‌ട്രീം പോയിന്റല്ല. അതിനാൽ, ഒരു ഫംഗ്‌ഷന്റെ എക്‌സ്‌ട്രീം കണ്ടെത്തുന്നതിന്, നിങ്ങൾ ഫംഗ്‌ഷന്റെ എല്ലാ നിർണായക പോയിന്റുകളും കണ്ടെത്തേണ്ടതുണ്ട്, തുടർന്ന് ഈ പോയിന്റുകൾ ഓരോന്നും പരമാവധി, മിനിമം എന്നിവയ്ക്കായി പ്രത്യേകം പരിശോധിക്കുക. ഇനിപ്പറയുന്ന സിദ്ധാന്തം ഈ ലക്ഷ്യം നിറവേറ്റുന്നു.

സിദ്ധാന്തം 2. (ഒരു തീവ്രതയുടെ നിലനിൽപ്പിന് മതിയായ അവസ്ഥ.)നിർണ്ണായക പോയിന്റ് അടങ്ങുന്ന ചില ഇടവേളകളിൽ പ്രവർത്തനം തുടർച്ചയായിരിക്കട്ടെ x 0, ഈ ഇടവേളയുടെ എല്ലാ പോയിന്റുകളിലും (ഒരുപക്ഷേ, പോയിന്റ് ഒഴികെ) വ്യത്യാസപ്പെട്ടിരിക്കുന്നു x 0). ഈ പോയിന്റിലൂടെ ഇടത്തുനിന്ന് വലത്തോട്ട് നീങ്ങുമ്പോൾ, ഡെറിവേറ്റീവ് ചിഹ്നത്തെ പ്ലസ് മുതൽ മൈനസിലേക്ക് മാറ്റുകയാണെങ്കിൽ, പോയിന്റിൽ x = x 0 ഫംഗ്‌ഷന് പരമാവധി ഉണ്ട്. എങ്കിൽ, കടന്നുപോകുമ്പോൾ x 0 ഇടത്തുനിന്ന് വലത്തോട്ട്, ഡെറിവേറ്റീവ് സൈൻ മൈനസിൽ നിന്ന് പ്ലസിലേക്ക് മാറ്റുന്നു, തുടർന്ന് ഫംഗ്‌ഷന് ഈ ഘട്ടത്തിൽ മിനിമം ഉണ്ട്.

അങ്ങനെ, എങ്കിൽ

തെളിവ്. കടന്നുപോകുമ്പോൾ നമുക്ക് ആദ്യം ഊഹിക്കാം x 0 ഡെറിവേറ്റീവ് മാറ്റങ്ങളുടെ ചിഹ്നം പ്ലസ് മുതൽ മൈനസ് വരെ, അതായത്. എല്ലാവരുടെയും മുന്നിൽ x, പോയിന്റിനോട് അടുത്ത് x 0 f "(x)> 0 വേണ്ടി x< x 0 , f "(x)< 0 വേണ്ടി x>x 0 . വ്യത്യാസത്തിന് ലഗ്രാഞ്ചിന്റെ സിദ്ധാന്തം പ്രയോഗിക്കാം f(x) - f(x 0 ) = f "(c)(x- x 0), എവിടെ സിഇടയിൽ കിടക്കുന്നു xഒപ്പം x 0 .

1. അനുവദിക്കുക x< x 0 . പിന്നെ സി< x 0 ഒപ്പം f "(സി)> 0. അതുകൊണ്ടാണ് f "(c)(x- x 0)< 0 അതിനാൽ

   f(x) - f(x 0 )< 0, അതായത്. f(x)< f(x 0 ).

2. അനുവദിക്കുക x > x 0 . പിന്നെ c>x 0 ഒപ്പം f "(സി)< 0. അർത്ഥമാക്കുന്നത് f "(c)(x- x 0)< 0. അതുകൊണ്ടാണ് f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

അങ്ങനെ, എല്ലാ മൂല്യങ്ങൾക്കും xവേണ്ടത്ര അടുത്ത് x 0 f(x)< f(x 0 ) . ഈ പോയിന്റിൽ എന്നാണ് x 0 ഫംഗ്‌ഷന് പരമാവധി ഉണ്ട്.

മിനിമം സിദ്ധാന്തത്തിന്റെ രണ്ടാം ഭാഗം സമാനമായ രീതിയിൽ തെളിയിക്കപ്പെട്ടിരിക്കുന്നു.



ചിത്രത്തിൽ ഈ സിദ്ധാന്തത്തിന്റെ അർത്ഥം നമുക്ക് ചിത്രീകരിക്കാം. അനുവദിക്കുക f "(x 1 ) =0 കൂടാതെ ഏതിനും x,വേണ്ടത്ര അടുത്ത് x 1, അസമത്വങ്ങൾ തൃപ്തികരമാണ്

f "(x)< 0-ന് x< x 1 , f "(x)> 0-ന് x>x 1 .

തുടർന്ന് പോയിന്റിന്റെ ഇടതുവശത്തേക്ക് x 1 ഫംഗ്ഷൻ വലതുവശത്ത് കൂടുകയും കുറയുകയും ചെയ്യുന്നു, അതിനാൽ, എപ്പോൾ x = x 1 ഫംഗ്‌ഷൻ കൂടുന്നതിൽ നിന്ന് കുറയുന്നതിലേക്ക് പോകുന്നു, അതായത്, ഇതിന് പരമാവധി ഉണ്ട്.

അതുപോലെ, നമുക്ക് പോയിന്റുകൾ പരിഗണിക്കാം x 2 ഒപ്പം x 3 .


മുകളിൽ പറഞ്ഞവയെല്ലാം ചിത്രത്തിൽ സ്കീമാറ്റിക് ആയി ചിത്രീകരിക്കാം:

എക്സ്ട്രീം എന്ന ഫംഗ്‌ഷൻ y=f(x) പഠിക്കുന്നതിനുള്ള നിയമം

1. ഒരു ഫംഗ്ഷന്റെ ഡൊമെയ്ൻ കണ്ടെത്തുക f(x).
2. ഒരു ഫംഗ്‌ഷന്റെ ആദ്യ ഡെറിവേറ്റീവ് കണ്ടെത്തുക f "(x).
3. ഇതിനായി നിർണായക പോയിന്റുകൾ നിർണ്ണയിക്കുക:
   1. സമവാക്യത്തിന്റെ യഥാർത്ഥ വേരുകൾ കണ്ടെത്തുക f "(x)=0;
   2. എല്ലാ മൂല്യങ്ങളും കണ്ടെത്തുക xഅതിനായി ഡെറിവേറ്റീവ് f "(x)നിലവിലില്ല.
4. നിർണായക പോയിന്റിന്റെ ഇടത്തോട്ടും വലത്തോട്ടും ഡെറിവേറ്റീവിന്റെ അടയാളം നിർണ്ണയിക്കുക. രണ്ട് നിർണായക പോയിന്റുകൾക്കിടയിൽ ഡെറിവേറ്റീവിന്റെ ചിഹ്നം സ്ഥിരമായി നിലനിൽക്കുന്നതിനാൽ, നിർണ്ണായക പോയിന്റിന്റെ ഇടതുവശത്ത് ഒരു പോയിന്റിലും വലതുവശത്ത് ഒരു പോയിന്റിലും ഡെറിവേറ്റീവിന്റെ അടയാളം നിർണ്ണയിക്കാൻ മതിയാകും.
5. എക്സ്ട്രീം പോയിന്റുകളിൽ ഫംഗ്ഷന്റെ മൂല്യം കണക്കാക്കുക.

ഉദാഹരണങ്ങൾ. ഏറ്റവും കുറഞ്ഞതും കൂടിയതുമായ പ്രവർത്തനങ്ങൾ പര്യവേക്ഷണം ചെയ്യുക.




ഒരു സെഗ്‌മെന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ പരമാവധി, ചെറിയ മൂല്യങ്ങൾ

ഏറ്റവും വലിയഒരു ഇടവേളയിലെ ഒരു ഫംഗ്‌ഷന്റെ മൂല്യം ഈ ഇടവേളയിലെ അതിന്റെ എല്ലാ മൂല്യങ്ങളിലും ഏറ്റവും വലുതാണ്, കൂടാതെ ഏറ്റവും ചെറിയ- അതിന്റെ എല്ലാ മൂല്യങ്ങളിലും ഏറ്റവും ചെറുത്.

പ്രവർത്തനം പരിഗണിക്കുക y=f(x)വിഭാഗത്തിൽ തുടർച്ചയായി [ എ, ബി]. അറിയപ്പെടുന്നതുപോലെ, അത്തരം ഒരു ഫംഗ്ഷൻ അതിന്റെ പരമാവധി, കുറഞ്ഞ മൂല്യങ്ങളിൽ എത്തുന്നു, സെഗ്മെന്റിന്റെ അതിർത്തിയിലോ അതിനുള്ളിലോ. ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും വലുതോ ചെറുതോ ആയ മൂല്യം സെഗ്‌മെന്റിന്റെ ഒരു ആന്തരിക പോയിന്റിൽ നേടിയാൽ, ഈ മൂല്യം ഫംഗ്‌ഷന്റെ പരമാവധി അല്ലെങ്കിൽ കുറഞ്ഞതാണ്, അതായത്, ഇത് നിർണായക പോയിന്റുകളിൽ നേടുന്നു.

അങ്ങനെ, നമുക്ക് ഇനിപ്പറയുന്നവ ലഭിക്കും ഒരു സെഗ്‌മെന്റിൽ ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും വലുതും ചെറുതുമായ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിനുള്ള നിയമം[ എ, ബി] :

1. ഇടവേളയിൽ ഫംഗ്‌ഷന്റെ എല്ലാ നിർണായക പോയിന്റുകളും കണ്ടെത്തുക ( എ, ബി) കൂടാതെ ഈ പോയിന്റുകളിലെ ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ കണക്കാക്കുക.
2. എപ്പോൾ സെഗ്‌മെന്റിന്റെ അറ്റത്തുള്ള ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ കണക്കാക്കുക x = a, x = b.
3. ലഭിച്ച എല്ലാ മൂല്യങ്ങളിൽ നിന്നും, ഏറ്റവും വലുതും ചെറുതും തിരഞ്ഞെടുക്കുക.