Birkaç tür var mantıksızlık kesirler paydada. Bir veya daha fazla cebirsel kökün varlığı ile ilişkilidir. farklı dereceler. Kurtulmak için mantıksızlık duruma göre bazı matematiksel işlemlerin yapılması gerekmektedir.

Talimatlar

1. Kurtulmadan önce mantıksızlık kesirler paydada türünü belirlemeli ve buna bağlı olarak çözüme devam etmelisiniz. Gerçekten de, herhangi bir mantıksızlık, köklerin basit varlığından kaynaklanır; bunların farklı kombinasyonları ve dereceleri, farklı algoritmalar tarafından varsayılır.

2. Paydanın karekökü, a/?b formunun ifadesi?b'ye eşit bir ek faktör girin. Kesrin değişmemesi için hem payı hem de paydayı çarpmak gerekir: a/?b ? (a ?b)/b.Örnek 1: 10/?3 ? (10?3)/3.

3. Çizginin altındaki mevcudiyet kesirler kök kesirli güç m/n ve n>m biçimindedir. Bu ifade şuna benzer: a/?(b^m/n).

4. Benzerlerinden kurtulun mantıksızlık ayrıca bir çarpan girerek bu sefer daha zor: b^(n-m)/n, yani. kökün üssünden, ifadenin derecesini işaretinin altında çıkarmak gerekir. O zaman paydada yalnızca birinci kuvvet kalacak: a/(b^m/n) ? a ?(b^(n-m)/n)/b. Örnek 2: 5/(4^3/5) ? 5 ?(4^2/5)/4 = 5 ?(16^1/5)/4.

5. Toplam Karekök Her iki bileşeni de çarpın kesirler benzer bir farkla. Daha sonra köklerin irrasyonel olarak toplanmasından payda, kök işareti altındaki ifadelerin/sayıların farkına dönüştürülür: a/(?b + ?c) ? a (?b - ?c)/(b - c).Örnek 3: 9/(?13 + ?23) ? 9 (?13 - ?23)/(13 - 23) = 9 (?23 - ?13)/10.

6. Küp köklerin toplamı/farkı Payda bir toplam içeriyorsa farkın tamamlanmamış karesini ek faktör olarak seçin ve buna göre köklerin farkı için toplamın tamamlanmamış karesini seçin: a/(?b ± ?c) ? a (?b? ? ?(b c) + ?c?)/ ((?b ± ?c) ?b? ? ?(b c) + ?c?) ?a (?b? ? ?(b c) + ? c?)/(b ± c).Örnek 4: 7/(?5 + ?4) ? 7 (?25-?20 +?16)/9.

7. Sorun hem kare hem de küp kök içeriyorsa çözümü iki aşamaya bölün: paydadan adım adım türetin Kare kök ve ondan sonra kübik. Bu, zaten bildiğiniz yöntemlere göre yapılır: ilk eylemde köklerin farkının/toplamının çarpanını, ikincisinde ise toplamın/farkın tamamlanmamış karesini seçmeniz gerekir.

İpucu 2: Paydadaki mantıksızlıktan nasıl kurtuluruz

Doğru giriş kesirli sayı içermiyor mantıksızlık V payda. Böyle bir gösterimin görünüşte anlaşılması daha kolaydır, bu nedenle mantıksızlık V payda Ondan kurtulmak akıllıcadır. Bu durumda irrasyonellik pay haline gelebilir.

Talimatlar

1. Başlangıç ​​olarak ilkel bir örneğe bakalım: 1/sqrt(2). 2'nin karekökü irrasyonel bir sayıdır payda.Bu durumda kesrin payını ve paydasını paydasıyla çarpmanız gerekir. Bu makul bir sayı sağlayacaktır. payda. Aslında, sqrt(2)*sqrt(2) = sqrt(4) = 2. 2 özdeş karekökün birbiriyle çarpılması, tüm köklerin altında ne olduğuna yol açacaktır: bu durumda- iki Sonuç olarak: 1/sqrt(2) = (1*sqrt(2))/(sqrt(2)*sqrt(2)) = sqrt(2)/2. Bu algoritma kesirler için de uygundur. payda kök makul bir sayı ile çarpılır. Bu durumda pay ve payda, içinde bulunan kök ile çarpılmalıdır. payda.Örnek: 1/(2*sqrt(3)) = (1*sqrt(3))/(2*sqrt(3)*sqrt(3)) = sqrt(3)/(2*3) = sqrt( 3)/6.

2. Tabii eğer böyle bir şey yapılmalıysa payda Bulunan karekök değil, diyelim kübik kök veya başka bir derecedir. Köklenme payda aynı kökle çarpmak gerekir ve pay da aynı kökle çarpılır. Daha sonra kök paya girecektir.

3. Daha zor bir durumda payda bir irrasyonel ve makul bir sayının veya 2 irrasyonel sayının toplamı veya farkı var. 2 karekök veya bir karekök ve makul bir sayının toplamı (farkı) durumunda, ünlü formülü (x+y) kullanabilirsiniz. )(x-y) = (x^2 )-(y^2). kurtulmanıza yardımcı olacaktır mantıksızlık V payda. Eğer içindeyse payda fark, o zaman pay ve paydayı aynı sayıların toplamı ile, eğer toplam ise farkla çarpmanız gerekir. Bu çarpılan toplam veya fark, aşağıdaki ifadeye eşlenik olarak adlandırılacaktır. payda.Bu şemanın sonucu örnekte açıkça görülmektedir: 1/(sqrt(2)+1) = (sqrt(2)-1)/(sqrt(2)+1)(sqrt(2)-1) = (sqrt(2 )-1)/((sqrt(2)^2)-(1^2)) = (sqrt(2)-1)/(2-1) = sqrt(2)-1.

4. Eğer içindeyse payda kökün bulunduğu bir toplam (fark) var daha büyük ölçüde, o zaman durum önemsiz hale gelir ve kurtuluş mantıksızlık V payda her zaman kabul edilemez

İpucu 3: Bir kesrin paydasındaki mantıksızlıktan kendinizi nasıl kurtarabilirsiniz?

Bir kesir, çizginin üst kısmında yer alan pay ve altta yer alan böldüğü paydadan oluşur. İrrasyonel sayı, formda temsil edilemeyen bir sayıdır kesirler payda bir tam sayı ve bir doğal sayı ile payda. Bu tür sayılar, örneğin 2'nin veya pi'nin kareköküdür. Geleneksel olarak mantıksızlıktan bahsederken payda, kök ima edilir.

Talimatlar

1. Paydayla çarparak irrasyonelliği ortadan kaldırın. Bu şekilde irrasyonellik paya aktarılacaktır. Pay ve payda aynı sayı ile çarpıldığında değer kesirler değişmez. Her payda bir kök ise bu seçeneği kullanın.

2. Köküne bağlı olarak pay ve paydayı paydayla gerekli sayıda çarpın. Kök kare ise, o zaman bir kez.

3. Karekök örneğini düşünün. (56-y)/√(x+2) kesrini alın. Bir payı (56-y) ve karekök olan irrasyonel bir paydası √(x+2) vardır.

4. Pay ve paydayı çarpın kesirler paydaya, yani √(x+2)'ye. Orijinal örnek (56-y)/√(x+2), ((56-y)*√(x+2))/(√(x+2)*√(x+2)) olacaktır. Sonuç ((56-y)*√(x+2))/(x+2) olacaktır. Şimdi kök payda ve payda mantıksızlık yoktur.

5. Her zaman payda değil kesirler her biri kökün altındadır. (x+y)*(x-y)=x²-y² formülünü kullanarak mantıksızlıktan kurtulun.

6. (56-y)/(√(x+2)-√y) kesirli örneği düşünün. İrrasyonel paydası 2 karekök farkını içerir. (x+y)*(x-y) oluşturmak için paydayı tamamlayın.

7. Paydayı köklerin toplamı ile çarpın. Değeri elde etmek için payı aynı ile çarpın kesirler değişmedi. Kesir şu şekilde olacaktır: ((56-y)*(√(x+2)+√y))/((√(x+2)-√y)*(√(x+2)+√y) ).

8. Yukarıdaki (x+y)*(x-y)=x²-y² özelliğinden yararlanın ve paydayı irrasyonellikten kurtarın. Sonuç ((56-y)*(√(x+2)+√y))/(x+2-y) olacaktır. Artık kök paydadır ve payda irrasyonellikten kurtulmuştur.

9. İÇİNDE zor vakalar gerektiği şekilde uygulayarak bu seçeneklerin her ikisini de tekrarlayın. Mantıksızlıktan kurtulmanın her zaman mümkün olmadığını unutmayın. payda .

Cebirsel kesir, A/B formundaki bir ifadedir; burada A ve B harfleri herhangi bir sayısal veya sayıyı temsil eder. gerçek ifadeler. Cebirsel kesirlerdeki pay ve payda genellikle büyük bir biçime sahiptir, ancak bu tür kesirlerle yapılan işlemler, pay ve paydanın pozitif tamsayılar olduğu sıradan işlemlerle aynı kurallara göre yapılmalıdır.

Talimatlar

1. Karışık verilirse kesirler, bunları düzensiz kesirlere dönüştürün (payın paydadan büyük olduğu kesir): paydayı tam kısımla çarpın ve payı ekleyin. Yani 2 1/3 sayısı 7/3'e dönüşecek. Bunu yapmak için 3'ü 2 ile çarpın ve bir ekleyin.

2. Bir ondalık sayıyı uygunsuz bir kesire dönüştürmeniz gerekiyorsa, bunu, ondalık noktası olmayan bir sayıyı, virgülden sonraki sayılar kadar sıfır içeren bir sayıya bölmek olarak düşünün. Diyelim ki 2,5 sayısını 25/10 (kısaltırsanız 5/2 elde edersiniz), 3,61 sayısını da 361/100 olarak düşünün. Uygunsuz kesirlerle işlem yapmak genellikle karışık veya ondalık kesirlerle işlem yapmaktan daha kolaydır.

3. Kesirlerin paydaları aynıysa ve bunları toplamanız gerekiyorsa payları eklemeniz yeterlidir; paydalar değişmeden kalır.

4. Paydaları aynı olan kesirleri çıkarmanız gerekiyorsa, 2. kesrin payını birinci kesrin payından çıkarın. Paydalar da değişmez.

5. Kesirleri eklemeniz veya bir kesri diğerinden çıkarmanız gerekiyorsa ve bunların paydaları farklıysa, kesirleri ortak bir paydaya düşürün. Bunu yapmak için, her iki paydanın en küçük evrensel katı (LCM) veya kesirler 2'den büyükse birkaçı olacak bir sayı bulun. LCM, verilen tüm kesirlerin paydalarına bölünecek bir sayıdır. Örneğin 2 ve 5 için bu sayı 10'dur.

6. Eşittir işaretinden sonra yatay bir çizgi çizin ve bu sayıyı (NOC) paydaya yazın. Terimin tamamına ek faktörler ekleyin - LCM'yi elde etmek için hem payı hem de paydayı çarpmanız gereken sayı. Toplama veya çıkarma işaretini koruyarak payları adım adım ek faktörlerle çarpın.

7. Toplamı hesaplayın, gerekirse azaltın veya parçanın tamamını seçin. Örneğin katlamanız mı gerekiyor? Ve?. Her iki fraksiyon için LCM 12'dir. Bu durumda, ilk fraksiyon için ek faktör 4, 2. fraksiyon için ise - 3'tür. Toplam: ?+?=(1·4+1·3)/12=7/12.

8. Çarpma işlemine örnek verilirse payları (toplamın payı olacak) ve paydaları (toplamın paydası olacak) birlikte çarpın. Bu durumda bunları ortak bir paydaya indirgemeye gerek yoktur.

9. Bir kesri bir kesire bölmek için ikinci kesri ters çevirip kesirleri çarpmanız gerekir. Yani, a/b: c/d = a/b · d/c.

10. Pay ve paydayı gerektiği gibi çarpanlara ayırın. Örneğin, evrensel faktörü parantezden çıkarın veya kısaltılmış çarpma formüllerine göre genişletin, böylece gerekirse pay ve paydayı minimum evrensel bölen olan GCD'ye göre azaltabilirsiniz.

Not!
Sayıları sayılarla, aynı türdeki harfleri aynı türdeki harflerle toplayın. Diyelim ki 3a ve 4b'yi toplamak imkansız, bu da toplamlarının veya farklarının payda - 3a±4b kalacağı anlamına geliyor.

Günlük yaşamda sahte sayılar daha yaygındır: 1, 2, 3, 4 vb. (5 kg patates) ve kesirli, tam sayı olmayan sayılar (5,4 kg soğan). Birçoğu şu şekilde sunulmaktadır: biçim ondalık sayılar. Ancak ondalık kesri temsil edin biçim kesirlerçok kolay.

Talimatlar

1. Diyelim ki "0,12" sayısı verildi. Bu ondalık kesri azaltmaz ve olduğu gibi sunmazsanız, şu şekilde görünecektir: 12/100 (“on iki yüzde biri”). Paydadaki yüzden kurtulmak için hem payı hem de paydayı tam sayılara bölen bir sayıya bölmeniz gerekir. Bu sayı 4'tür. Daha sonra pay ve paydayı bölerek sayıyı elde ederiz: 3/25.

2. Günlük hayata daha fazla baktığımızda, çoğu zaman ürünlerin fiyat etiketlerinde ağırlığının örneğin 0,478 kg veya benzeri olduğunu görebiliriz.Bu rakamı hayal etmek de kolaydır. biçim kesirler:478/1000 = 239/500. Bu kesir oldukça çirkindir ve eğer bir olasılık olsaydı, bu ondalık kesrin daha da azaltılmasına izin verilirdi. Ve hepsi aynı şekilde: Hem payı hem de paydayı bölen bir sayı seçmek. Bu sayıya en büyük evrensel faktör denir. Faktöre "en büyük" adı verilmesinin nedeni, hem pay hem de paydayı (ilk örnekte olduğu gibi) hemen 4'e bölmenin, iki kere 2'ye bölmekten çok daha uygun olmasıdır.

Konuyla ilgili video

Ondalık kesir- çeşitlilik kesirler Paydasında "yuvarlak" bir sayı bulunan: 10, 100, 1000 vb., Diyelim ki, kesir 5/10'un ondalık gösterimi 0,5'tir. Bu teze dayanarak, kesir ondalık sayı olarak temsil edilebilir kesirler .

Talimatlar

1. Mümkün, ondalık sayı olarak gösterilmesi gerekiyor kesir 18/25 Öncelikle paydada “yuvarlak” sayılardan birinin göründüğünden emin olmanız gerekir: 100, 1000, vb. Bunu yapmak için paydayı 4 ile çarpmanız gerekir. Ancak hem payı hem de paydayı 4 ile çarpmanız gerekir.

2. Pay ve paydanın çarpılması kesirler 18/25'e 4, 72/100 çıkıyor. Bu kaydedildi kesir ondalık biçimde: 0,72.

Elinde hesap makinesi olmadığında 2 ondalık kesirleri bölme işleminde birçok kişi bazı zorluklarla karşılaşıyor. Burada gerçekten zor olan hiçbir şey yok. Ondalık kesirler paydası 10'un katı olan bir sayıya sahipse böyle denir. Her zamanki gibi bu sayılar tek satıra yazılır ve kesirli kısmı bütünden ayıran virgül bulunur. Görünüşe göre, ondalık noktadan sonraki basamak sayısında da farklılık gösteren kesirli bir parçanın varlığı nedeniyle, bu tür sayılarla matematiksel işlemlerin hesap makinesi olmadan nasıl gerçekleştirileceği pek çok kişi için açık değil.

İhtiyacın olacak

• kağıt parçası, kalem

Talimatlar

1. Bir ondalık kesri diğerine bölmek için, her iki sayıya da bakmanız ve hangisinin virgülden sonra daha fazla rakama sahip olduğunu belirlemeniz gerektiği ortaya çıktı. Her iki sayıyı da 10'un katı olan bir sayıyla çarpıyoruz, yani. 10, 1000 veya 100000, içindeki sıfırların sayısı eşittir Daha ilk 2 sayımızdan birinin ondalık noktasından sonraki basamaklar. Şimdi ikisi de ondalık kesirler sıradan tamsayılara dönüştü. Kalemle bir kağıt alın ve elde edilen iki sayıyı bir "köşe" ile ayırın. Sonucu alıyoruz.

2. Diyelim ki 7,456 sayısını 0,43'e bölmemiz gerekiyor. İlk sayının ondalık basamağı daha fazla (3 ondalık basamak), bu nedenle her iki sayıyı da 1000 ile çarpmıyoruz ve iki ilkel tam sayı elde ediyoruz: 7456 ve 430. Şimdi 7456'yı 430'a bir “köşe” ile bölüyoruz ve 7.456 bölünürse bunu elde ediyoruz 0,43'e gelindiğinde yaklaşık 17,3 çıkacaktır.

3. Başka bir bölme yöntemi daha var. Ondalık sayıların yazılması kesirler pay ve paydası olan ilkel kesirler şeklinde, bizim durumumuz için bunlar 7456/1000 ve 43/100'dür. Daha sonra 2 ilkel kesri bölmek için gereken ifadeyi yazıyoruz: 7456*100/1000*43, onlukları indirdikten sonra şunu elde ediyoruz: 7456/10*43 = 7456/430 Son çıktıda yine bölme işlemini elde ediyoruz. Bir “köşe” ile yapılabilecek 2 ilkel sayı 7456 ve 430.

Konuyla ilgili video

Yararlı tavsiye
Dolayısıyla ondalık kesirleri bölmenin yolu, her birinin aynı sayıyla çarpılması desteğiyle tam sayılara indirgemektir. Tamsayılarla işlem yapmak her zamanki gibi kimseye zorluk çıkarmaz.

Konuyla ilgili video

Paydası irrasyonel bir ifade içeren kesirli cebirsel bir ifadeyi dönüştürürken, genellikle kesir, paydası rasyonel olacak şekilde temsil edilmeye çalışılır. Eğer A,B,C,D,... bazısı ise cebirsel ifadeler, daha sonra formun ifadelerinin paydasındaki radikal işaretlerden kurtulabileceğiniz kuralları belirleyebilirsiniz.

Tüm bu durumlarda, irrasyonellikten kurtuluş, kesrin pay ve paydasının, kesrin paydasıyla çarpımı rasyonel olacak şekilde seçilen bir faktörle çarpılmasıyla sağlanır.

1) Kesirli formun paydasındaki irrasyonellikten kurtulmak. Pay ve paydayı şununla çarpın:

Örnek 1. .

2) Formun kesirli olması durumunda. Pay ve paydayı irrasyonel bir faktörle çarpın

sırasıyla, yani eşlenik irrasyonel ifadeye.

Son eylemin anlamı, paydada toplamın ve farkın çarpımının kareler farkına dönüştürülmesidir ki bu zaten rasyonel bir ifade olacaktır.

Örnek 2. İfadenin paydasındaki mantıksızlıktan kendinizi kurtarın:

Çözüm, a) Kesrin pay ve paydasını ifadeyle çarpın. Alırız (bu şartıyla)

3) Aşağıdaki gibi ifadeler olması durumunda

payda bir toplam (fark) olarak kabul edilir ve küplerin ((20.11), (20.12) toplamını (farkını) elde etmek için farkın (toplam) kısmi karesi ile çarpılır. Pay da aynı faktörle çarpılır.

Örnek 3. İfadelerin paydasındaki mantıksızlıktan kendinizi kurtarın:

Çözüm, a) Bu kesrin paydasını sayılar ve 1'in toplamı olarak kabul edersek pay ve paydayı bu sayıların farkının kısmi karesi ile çarpın:

veya son olarak:

Bazı durumlarda, zıt nitelikte bir dönüşüm gerçekleştirmek gerekir: kesri paydaki irrasyonellikten kurtarmak. Tamamen aynı şekilde gerçekleştirilir.

Örnek 4. Bir kesrin payı konusunda kendinizi mantıksızlıktan kurtarın.

Ders No. 1 Ders konusu: “Kesrin paydasındaki irrasyonellikten kurtuluş”

Hedefler:

Eğitici:

Gelişimsel:

Eğitici: Eylemlerinizde tutarlılığı teşvik etmek.

Ders türü: yeni şeyler öğrenmek

Ders standardı:

mantıksızlıktan kurtulmanın bir yolunu bulabilmek

“Eşlenik ifadenin” anlamını anlamak

paydadaki irrasyonellikten kurtulabilecektir.

Teçhizat: bağımsız çalışma için kartlar.

Dersler sırasında

Köklerin nasıl çıkarılacağını biliyor musun? - öğretmene sorar

Evet elbette. Bitkinin sapını daha sert çekmeniz gerekir, kökü topraktan çıkarılacaktır.

Hayır, başka bir kökü kastettim, örneğin dokuzdan.

“th” bir son ek olduğu için “dokuz” olacaktır.

Karekökten bahsediyorum.

Karekök yoktur. Lifli ve çubuk şeklindedirler.

Dokuzun aritmetik karekökü.

Bunu söylerlerdi! Dokuzun karekökü = 3!

Köklerin nasıl çıkarılacağını biliyor musun?

2. “Tekrar öğrenmenin anasıdır.”

(8 dakika)

2. Evi/evi kontrol etmek№ 168 1)4; 2)10; 3)4;4) 8

3.Isın. Adımları izleyin (Slayt 1). Saat yönünün tersine bir daire çizin.

1. Bilinmeyen bir faktör seçin (Slayt2)

Gruplara ayırma: seçilen şekillere göre.

Yedek kompozisyon çiftlerini kontrol edin.

Bireysel olarak çalışırlar ve kontrol ederek puanları değerlendirirler.

(Ek 1)

3. “Kitap kitaptır ama aklınızı kullanın” (5 dakika)

(Slayt 3) İki arkadaş bir denklemi çözdü
ve farklı yanıtlar aldım. Bunlardan biri x ='i seçti , bir kontrol yaptım. İkincisi, ürünü şuna bölerek bilinmeyen faktörü buldu: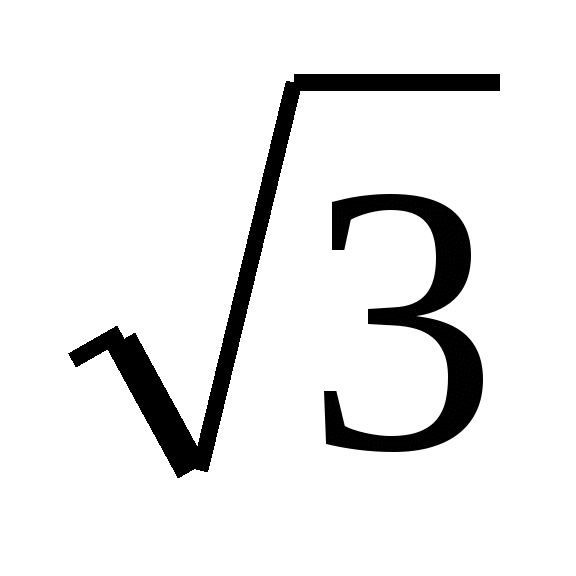
ve x = elde ettim 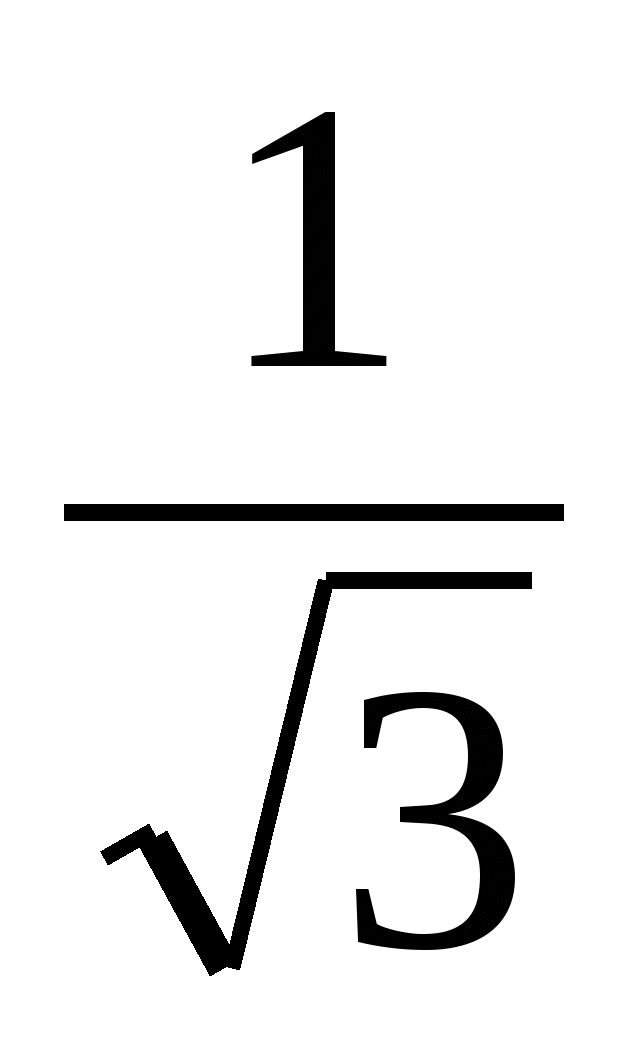. Hangisi doğrudur? Olabilmek Doğrusal Denklem iki kökü var mı? Hesaplamalar için en uygun ifade, paydada irrasyonellik içermeyen ifadedir.

Ders konusu(Slayt 4) : Bir kesrin paydasındaki irrasyonellikten kurtuluş

Hedefler(Slayt 5) : Bir kesrin paydalarındaki irrasyonellikten kurtulmanın yollarını öğrenin. Paydayı mantıksızlıktan kurtarma yeteneğini geliştirmek;

Vardiya çiftlerini çözün ve kontrol edin.

Durumu tartışırlar ve bir sonuca varırlar.

Konuyu yazın

Formüle et hedefler: Bir kesrin paydalarındaki irrasyonellikten kurtulmanın yollarını öğrenin.

kendinizi mantıksızlıktan kurtarmanın yolunu belirleme yeteneğini geliştirmek;

4. Yeni materyal üzerinde çalışın.

(10 dk)

Paydadaki irrasyonellikten nasıl kurtuluruz? Bilmek istiyor musun?

Gruplar halinde yeni materyaller üzerinde çalışmak

Grup performansı

Sabitleme (Slayt 6)

Destekleyici bir taslakla çalışırlar. (Ek 2)

Örnekleri çözün.

(Ek 3)

Bilgi alışverişi.

5. Şarj Etme (3 dakika)

Egzersiz yapmak

6. Bağımsız iş

(10 dk)

Çok seviyeli kartlara göre

1 inç:

2 inç:

3 inç:

Bireysel olarak gerçekleştirin, not defterlerini başka bir grupla değiştirerek kontrol edin.

Puanlar grubun puan kartına girilir.

(Ek 1)

7.Yaratıcı görev

(2 dakika)

Maymun - turuncu pazarlamacı (Slayt 7)

Bir kez benim kulübeme vardığımda,

Orada radikallerle ilgili bir sorun buldum.

Bunları her yere atmaya başladı.

Size soruyoruz kızlar ve erkekler,

Maymunun kuyruğundaki problemi çözün.

Bu konuyu incelemeyi bitirdiğimizi mi düşünüyorsunuz? Bir sonraki derste devam edelim.

Bir sonraki derste bununla ilgili neler öğreneceklerini konuşurlar.

8. Ödev: (2 dakika)

S.19 (Slayt 7)

Seviye 1: Sayı 170 (1-6)

Seviye 2: Sayı 170 (1-6 ve 9.12)

Yaratıcı görev: Martyshkin'in görevi.

Yaz

9. Ders özeti. Refleks

(3 dakika)

Seçilen ifadeye iki yıldız ve bir dilek etiketi eklenmiştir (Slayt 7)

Puanlar nota dönüştürülür ve öğretmene grup puan kartı verilir.

EK 1

Grup Puan Kartı.

0-8 puan

Bir çarpan seçin

0-8 puan

Bir grupta yeni materyal üzerinde çalışmak

0-5 puan

Kendim. İş

0-5 puan

Ders etkinliği

0-5 puan

EK 2

Destekleyici notlar

Payda ise cebirsel kesir karekök işareti içeriyorsa, paydanın irrasyonellik içerdiği söylenir. Bir ifadeyi, kesrin paydasında karekök işareti kalmayacak şekilde dönüştürmeye ne denir? paydadaki irrasyonellikten kurtuluş

Bu başlıkta yukarıda sıralanan irrasyonellik içeren üç limit grubunu da ele alacağız. $\frac(0)(0)$ formunda belirsizlik içeren limitlerle başlayalım.

Belirsizlik açıklaması $\frac(0)(0)$.

Çözüm diyagramı standart örnekler Bu tür genellikle iki adımdan oluşur:

• “Eşlenik” tabiriyle çarparak belirsizliğe yol açan mantıksızlıktan kurtuluyoruz;
• Gerekirse pay veya paydadaki (veya her ikisindeki) ifadeyi çarpanlarına ayırın;
• Belirsizliğe yol açan faktörleri azaltıp limitin istenilen değerini hesaplıyoruz.

Yukarıda kullanılan "eşlenik ifade" terimi örneklerde ayrıntılı olarak açıklanacaktır. Şimdilik bunun üzerinde ayrıntılı olarak durmanın bir anlamı yok. Genel olarak eşlenik ifadesini kullanmadan diğer yöne gidebilirsiniz. Bazen iyi seçilmiş bir değişim mantıksızlığı ortadan kaldırabilir. Bu tür örnekler standartlarda nadirdir testler bu nedenle, değiştirme kullanımı için yalnızca 6 numaralı örneği ele alacağız (bu konunun ikinci bölümüne bakın).

Aşağıda yazacağım birkaç formüle ihtiyacımız olacak:

\begin(equation) a^2-b^2=(a-b)\cdot(a+b) \end(equation) \begin(equation) a^3-b^3=(a-b)\cdot(a^2) +ab+b^2) \end(equation) \begin(equation) a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end(equation) \begin (denklem) a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end(denklem)

Ayrıca okuyucunun ikinci dereceden denklemlerin çözümüne ilişkin formülleri bildiğini varsayıyoruz. $x_1$ ve $x_2$ kök ise ikinci dereceden üç terimli$ax^2+bx+c$ ise aşağıdaki formül kullanılarak çarpanlara ayrılabilir:

\begin(equation) ax^2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end(denklem)

Şimdi geçeceğimiz standart problemleri çözmek için formüller (1)-(5) oldukça yeterlidir.

Örnek No.1

$\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)$'ı bulun.

Çünkü $\lim_(x\to 3)(\sqrt(7-x)-2)=\sqrt(7-3)-2=\sqrt(4)-2=0$ ve $\lim_(x\ to 3) (x-3)=3-3=0$ ise, verilen limitte $\frac(0)(0)$ formunda bir belirsizliğimiz var. $\sqrt(7-x)-2$ farkı bu belirsizliği ortaya çıkarmamızı engelliyor. Bu tür mantıksızlıklardan kurtulmak için “eşlenik ifade” olarak adlandırılan çarpma işlemine başvurulur. Şimdi bu çarpmanın nasıl çalıştığına bakacağız. $\sqrt(7-x)-2$ ile $\sqrt(7-x)+2$ ile çarpın:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)$$

Parantezleri açmak için, belirtilen formülün sağ tarafına $a=\sqrt(7-x)$, $b=2$ yazarak uygulayın:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)=(\sqrt(7-x))^2-2^2=7-x-4=3-x .$$

Gördüğünüz gibi payı $\sqrt(7-x)+2$ ile çarparsanız paydaki kök (yani irrasyonellik) ortadan kalkacaktır. Bu ifade $\sqrt(7-x)+2$ olacaktır birleşik$\sqrt(7-x)-2$ ifadesine. Ancak payı $\sqrt(7-x)+2$ ile çarpamayız, çünkü bu $\frac(\sqrt(7-x)-2)(x-3)$ kesirini değiştirecektir; sınırın altında. Hem pay hem de paydayı aynı anda çarpmanız gerekir:

$$ \lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)= \left|\frac(0)(0)\right|=\lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt(7-x)+2)) $$

Şimdi şunu hatırlayın $(\sqrt(7-x)-2)(\sqrt(7-x)+2)=3-x$ ve parantezleri açın. Parantezleri açtıktan ve $3-x=-(x-3)$ küçük bir dönüşümden sonra, kesri $x-3$ kadar azaltırız:

$$ \lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt( 7-x)+2))= \lim_(x\to 3)\frac(3-x)((x-3)\cdot(\sqrt(7-x)+2))=\\ =\lim_ (x\to 3)\frac(-(x-3))((x-3)\cdot(\sqrt(7-x)+2))= \lim_(x\to 3)\frac(-1 )(\sqrt(7-x)+2) $$

$\frac(0)(0)$ belirsizliği ortadan kalktı. Artık bu örneğin cevabını kolayca alabilirsiniz:

$$ \lim_(x\to 3)\frac(-1)(\sqrt(7-x)+2)=\frac(-1)(\sqrt(7-3)+2)=-\frac( 1)(\sqrt(4)+2)=-\frac(1)(4).$$

Eşlenik ifadenin, ne tür bir mantıksızlığı ortadan kaldırması gerektiğine bağlı olarak yapısını değiştirebileceğini belirtmek isterim. 4 ve 5 numaralı örneklerde (bu konunun ikinci kısmına bakınız) farklı türde bir eşlenik ifade kullanılacaktır.

Cevap: $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)=-\frac(1)(4)$.

Örnek No.2

$\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$'ı bulun.

Çünkü $\lim_(x\to 2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\sqrt(2^2+5)-\sqrt(7\cdot 2 ^) 2-19)=3-3=0$ ve $\lim_(x\to 2)(3x^2-5x-2)=3\cdot2^2-5\cdot 2-2=0$, o zaman şunu yaparız: $\frac(0)(0)$ biçimindeki belirsizlikle uğraşıyoruz. Bu kesrin paydasındaki irrasyonellikten kurtulalım. Bunu yapmak için $\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$ kesirinin hem payını hem de paydasını ekleriz. paydaya eşlenik $\sqrt(x^ 2+5)+\sqrt(7x^2-19)$ ifadesi:

$$ \lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\left|\frac(0 )(0)\right|= \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))) ((\sqrt(x^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))) $$

Yine 1 numaralı örnekte olduğu gibi genişletmek için parantez kullanmanız gerekiyor. Söz konusu formülün sağ tarafına $a=\sqrt(x^2+5)$, $b=\sqrt(7x^2-19)$ yazarsak payda için aşağıdaki ifadeyi elde ederiz:

$$ \left(\sqrt(x^2+5)-\sqrt(7x^2-19)\right)\left(\sqrt(x^2+5)+\sqrt(7x^2-19)\ sağ)=\\ =\left(\sqrt(x^2+5)\right)^2-\left(\sqrt(7x^2-19)\right)^2=x^2+5-(7x ^2-19)=-6x^2+24=-6\cdot(x^2-4) $$

Sınırımıza dönelim:

$$ \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))))((\sqrt(x) ^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))))= \lim_(x\to 2)\frac( (3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))(-6\cdot(x^2-4))=\\ =-\ frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x^2-4) $$

Örnek No. 1'de, eşlenik ifadeyle çarpmanın hemen ardından kesir azaltıldı. Burada, indirgemeden önce, $3x^2-5x-2$ ve $x^2-4$ ifadelerini çarpanlara ayırmanız ve ancak bundan sonra indirgemeye devam etmeniz gerekecektir. $3x^2-5x-2$ ifadesini çarpanlara ayırmak için kullanmanız gerekir. Önce karar verelim ikinci dereceden denklem$3x^2-5x-2=0$:

$$ 3x^2-5x-2=0\\ \begin(aligned) & D=(-5)^2-4\cdot3\cdot(-2)=25+24=49;\\ & x_1=\ frac(-(-5)-\sqrt(49))(2\cdot3)=\frac(5-7)(6)=-\frac(2)(6)=-\frac(1)(3) ;\\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot3)=\frac(5+7)(6)=\frac(12)(6)=2. \end(hizalanmış) $$

$x_1=-\frac(1)(3)$, $x_2=2$ yerine koyarsak, şunu elde ederiz:

$$ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)(x-2)=3\cdot\left(x+\ frac(1)(3)\right)(x-2)=\left(3\cdot x+3\cdot\frac(1)(3)\right)(x-2) =(3x+1)( x-2). $$

Şimdi $x^2-4$ ifadesini çarpanlara ayırmanın zamanı geldi. Bunun içine $a=x$, $b=2$ koyarak onu kullanalım:

$$ x^2-4=x^2-2^2=(x-2)(x+2) $$

Elde edilen sonuçları kullanalım. $x^2-4=(x-2)(x+2)$ ve $3x^2-5x-2=(3x+1)(x-2)$ olduğundan, o zaman:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2) -19))))(x^2-4) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x) ^2+5)+\sqrt(7x^2-19)))((x-2)(x+2)) $$

$x-2$ parantezini azaltarak şunu elde ederiz:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x^2+5)+\sqrt(7x^) 2-19))))((x-2)(x+2)) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt( x^2+5)+\sqrt(7x^2-19)))(x+2). $$

Tüm! Belirsizlik ortadan kalktı. Bir adım daha atıp cevaba geliyoruz:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x+2)=\\ =-\frac(1)(6)\cdot\frac((3\cdot 2+1)(\sqrt(2^2+5)+\sqrt(7\cdot 2) ^2-19))))(2+2)= -\frac(1)(6)\cdot\frac(7(3+3))(4)=-\frac(7)(4). $$

Cevap: $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=-\frac(7)( 4)$.

Aşağıdaki örnekte kesrin hem payında hem de paydasında irrasyonelliklerin mevcut olacağı durumu düşünün.

Örnek No.3

$\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9)'ı bulun ))$.

$\lim_(x\to 5)(\sqrt(x+4)-\sqrt(x^2-16))=\sqrt(9)-\sqrt(9)=0$ ve $\lim_( x olduğundan \to 5)(\sqrt(x^2-3x+6)-\sqrt(5x-9))=\sqrt(16)-\sqrt(16)=0$, o zaman $ formunda bir belirsizliğimiz var \frac (0)(0)$. Bu durumda kökler hem paydada hem de payda mevcut olduğundan belirsizlikten kurtulmak için aynı anda iki parantezle çarpmanız gerekecektir. Öncelikle $\sqrt(x+4)+\sqrt(x^2-16)$ ifadesine pay eşleniktir. Ve ikinci olarak, $\sqrt(x^2-3x+6)-\sqrt(5x-9)$ ifadesinin paydaya eşlenik olması.

$$ \lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9) ))=\left|\frac(0)(0)\right|=\\ =\lim_(x\to 5)\frac((\sqrt(x+4)-\sqrt(x^2-16) )(\sqrt(x+4)+\sqrt(x^2-16))(\sqrt(x^2-3x+6)+\sqrt(5x-9))))((\sqrt(x^2) -3x+6)-\sqrt(5x-9))(\sqrt(x^2-3x+6)+\sqrt(5x-9))(\sqrt(x+4)+\sqrt(x^2) -16))) $$ $$ -x^2+x+20=0;\\ \begin(aligned) & D=1^2-4\cdot(-1)\cdot 20=81;\\ & x_1=\frac(-1-\sqrt(81))(-2)=\frac(-10)(-2)=5;\\ & x_2=\frac(-1+\sqrt(81))( -2)=\frac(8)(-2)=-4. \end(aligned) \\ -x^2+x+20=-1\cdot(x-5)(x-(-4))=-(x-5)(x+4). $$

$x^2-8x+15$ ifadesi için şunu elde ederiz:

$$ x^2-8x+15=0;\\ \begin(aligned) & D=(-8)^2-4\cdot 1\cdot 15=4;\\ & x_1=\frac(-(-) 8)-\sqrt(4))(2)=\frac(6)(2)=3;\\ & x_2=\frac(-(-8)+\sqrt(4))(2)=\frac (10)(2)=5. \end(aligned)\\ x^2+8x+15=1\cdot(x-3)(x-5)=(x-3)(x-5). $$

Sonuçta ortaya çıkan $-x^2+x+20=-(x-5)(x+4)$ ve $x^2+8x+15=(x-3)(x-5)$ genişletmelerini limitte yerine koymak göz önünde bulundurularak aşağıdakilere sahip olacaktır:

$$ \lim_(x\to 5)\frac((-x^2+x+20)(\sqrt(x^2-3x+6)+\sqrt(5x-9))))((x^2 -8x+15)(\sqrt(x+4)+\sqrt(x^2-16))))= \lim_(x\to 5)\frac(-(x-5)(x+4)(\ sqrt(x^2-3x+6)+\sqrt(5x-9))))((x-3)(x-5)(\sqrt(x+4)+\sqrt(x^2-16)) )=\\ =\lim_(x\to 5)\frac(-(x+4)(\sqrt(x^2-3x+6)+\sqrt(5x-9))))((x-3) (\sqrt(x+4)+\sqrt(x^2-16))))= \frac(-(5+4)(\sqrt(5^2-3\cdot 5+6)+\sqrt(5) \cdot 5-9)))((5-3)(\sqrt(5+4)+\sqrt(5^2-16)))=-6. $$

Cevap: $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9) ))=-6$.

Bir sonraki (ikinci) kısımda, eşlenik ifadenin önceki problemlerden farklı bir forma sahip olacağı birkaç örneği daha ele alacağız. Unutulmaması gereken en önemli nokta, eşlenik ifade kullanmanın amacının belirsizliğe neden olan mantıksızlıktan kurtulmak olduğudur.

İsteğin üzerine!

5. Eşitsizliği çözün:

6 . Ifadeyi basitleştir:

17. f(x)=6x2 +8x+5, F(-1)=3. F(-2)'yi bulun.

F(-1) = 3 olduğunu bilerek C'yi bulalım.

3 = 2 ∙ (-1) 3 + 4 ∙ (-1) 2 + 5 ∙ (-1) + C;

3 = -2 + 4 – 5 + C;

Böylece ters türev F(x) = 2x 3 + 4x 2 + 5x + 6 olur. F(-2)'yi bulalım.

F(-2) = 2∙(-2) 3 +4∙(-2) 2 +5∙(-2)+6 = -16+16-10+6=-4.

20. Paydadaki mantıksızlıktan kurtulun

Çözüm, bir kesrin pay ve paydasının sıfırdan farklı aynı sayıyla çarpılmasına olanak tanıyan kesirin temel özelliğine dayanmaktadır. Bir kesrin paydasındaki radikal işaretlerden kurtulmak için genellikle kısaltılmış çarpma formülleri kullanılır. Sonuçta, iki radikalin farkı toplamlarıyla çarpılırsa, köklerin karelerinin farkını elde ederiz, yani. radikal işaretler olmayan bir ifade elde edersiniz.

21. Ifadeyi basitleştir:

Bu örneği iki şekilde çözelim. 1) İkinci faktörün radikal ifadesini iki ifadenin toplamının karesi şeklinde hayal edelim, yani. (a + b) 2 formunda. Bu, aritmetik karekökü çıkarmamızı sağlayacaktır.

2) Birinci faktörün karesini alalım ve ikinci faktörün aritmetik karekökünün işaretinin altına koyalım.

Size uygun olana karar verin!

22. (x 1 ∙y 1 +x 2 ∙y 2)'yi bulun; burada (x n; y n) denklem sisteminin çözümleridir:

Aritmetik karekök yalnızca negatif olmayan bir sayıdan alınabileceğinden, o zaman kabul edilebilir değerler değişken en eşitsizliği sağlayan tüm sayılar y≥0. Sistemin ilk denklemindeki ürün eşit olduğundan negatif sayı ise aşağıdaki koşulun yerine getirilmesi gerekir: X<0 . Hadi ifade edelim X birinci denklemden alıp değerini ikinci denklemde yerine koy. Ortaya çıkan denklemi çözelim en ve ardından değerleri bulun X daha önce elde edilen değerlere karşılık gelen en.

23. Eşitsizliği çözün: 7sin 2 x+cos 2 x>5sinx.

Temel trigonometrik özdeşliğe göre: sin 2 x+cos 2 x=1 olduğundan, bu eşitsizliği 6sin 2 x+ sin 2 x +cos 2 x>5sinx şeklinde gösterip, ana denklemi uyguluyoruz. trigonometrik özdeşlik, şunu elde ederiz: 6sin 2 x+ 1>5sinx. Eşitsizliği çözme:

6sin 2 x-5sinx+1 >0. Şimdi yerine şunu koyalım: sinx=y ve ikinci dereceden bir eşitsizlik elde edelim:

6y 2 -5y+1>0. Bu eşitsizliği sol tarafı çarpanlara ayırarak aralık yöntemini kullanarak çözelim. Bunu yapmak için ikinci dereceden denklemin tamamının köklerini buluyoruz:

6y 2 -5y+1=0. Diskriminant D=b 2 -4ac=5 2 -4∙6∙1=25-24=1. Sonra y 1 ve y 2'yi elde ederiz:

24. Sağ prizmanın tabanında alanı 300 cm3 olan normal bir üçgen bulunur. Prizmanın yan yüzeyinin alanını hesaplayın.

Tabanında doğru Δ ABC'nin bulunduğu normal bir üçgen prizma ABCA 1 B 1 C 1 verilsin, alanı bizim tarafımızdan bilinmektedir. Eşkenar üçgenin alan formülünü kullanarak ABC üçgenimizin kenarını buluyoruz. Düz bir prizmanın hacmi V=S ana formülüyle hesaplandığı için. ∙ H ve biz de biliyoruz, o zaman H'yi bulabiliriz - prizmanın yüksekliğini. Prizmanın yan kenarı prizmanın yüksekliğine eşit olacaktır: AA 1 =H. Tabanın yanını ve prizmanın yan kenarının uzunluğunu bilerek, yan yüzeyinin alanını şu formülü kullanarak bulabilirsiniz: S tarafı. =P temel ∙ H.

25. Okul sınavında 20 soru vardı. Her doğru cevap için katılımcıya 12 puan verildi ve her yanlış cevap için 10 puan düşürüldü. Katılımcılardan biri tüm soruları yanıtlayıp 86 puan aldığına göre kaç doğru cevap vermiştir?

Katılımcının x doğru cevap vermesine izin verin. O zaman (20) yanlış cevabı var. Her doğru cevap için kendisine 12 puan verildiğini ve her yanlış cevap için 10 puan düşüldüğünü ve aynı zamanda 86 puan aldığını bilerek denklemi oluşturacağız:

12x-10·(20'ler)=86;

12x-200+10x=86;

22x=286 ⇒ x=286:22 ⇒ x=13. Katılımcı 13 doğru cevap vermiştir.

UNT'deki matematik sınavına 25 doğru cevap vermenizi diliyorum!

24. Düzgün bir dörtgen piramitte yükseklik 3, yan kenar 6'dır. Piramidin çevresini saran kürenin yarıçapını bulun.

Merkezi O 1 noktasında ve yarıçapı MO 1 olan, yüksekliği MO=3 ve yan kenarı MA=6 olan düzgün bir MABCD piramidi etrafında tanımlansın. MO 1 topunun yarıçapını bulmak gerekir. MM1 tarafının topun çapı olduğu ΔMAM 1'i düşünün. O halde ∠MAM 1 =90°. MA kenarı ve bu MO kenarının hipotenüse izdüşümü biliniyorsa, MM 1 hipotenüsünü bulalım. Hatırlamak? Tepe noktasından çizilen yükseklik dik açı hipotenüsün bir ortalaması var oransal değer bacakların hipotenüse izdüşümleri arasındaki ve her bacak, tüm hipotenüs ile bu bacağın hipotenüse izdüşümü arasındaki ortalama orantılı değerdir. Bu görevde kuralın sadece altı çizili kısmı işimize yarayacaktır.

Eşitliği yazıyoruz: MA 2 =MO∙MM 1. Verilerimizi yerine koyarız: 6 2 =3∙MM 1. Dolayısıyla MM 1 =36:3=12. Topun çapını yani MO 1 =6'nın yarıçapını bulduk.

25. Petya, Misha'dan daha yaşlı olan Kolya'dan daha yaşlı, Masha, Kolya'dan daha yaşlı ve Dasha, Petya'dan daha genç ama Masha'dan daha yaşlı. Üçüncü en yaşlı kim?

Diyelim ki: daha yaşlı olmak daha çok şey ifade ediyor. Petya, Misha'dan daha yaşlı olan Kolya'dan daha yaşlıŞöyle yazalım: Petya>Kolya>Misha. Dasha Petya'dan daha genç ama Masha'dan daha yaşlışöyle yazalım: Maşa<Даша<Петя, что будет равнозначно записи: Петя>Dasha>Maşa. Çünkü Masha Kolya'dan daha yaşlı sonra şunu elde ederiz: Petya>Dasha>Masha>Kolya. Ve son olarak: Petya>Dasha>Masha>Kolya>Misha. Böylece üçüncü en eskisi Masha'dır.

UNT'ye başarılı bir hazırlık yapmanızı diliyorum!