Der er flere typer irrationalitet brøker i nævneren. Det er forbundet med tilstedeværelsen i det af en algebraisk rod af en eller forskellige grader. For at slippe af med irrationalitet, er det nødvendigt at udføre visse matematiske operationer afhængigt af situationen.

Instruktioner

1. Inden man slipper af med irrationalitet brøker i nævneren skal du bestemme dens type, og afhængigt af dette fortsætte med løsningen. Faktisk følger enhver irrationalitet af den simple tilstedeværelse af rødder; deres forskellige kombinationer og grader antages af forskellige algoritmer.

2. Kvadratroden af ​​nævneren, udtryk for formen a/?b Indtast en ekstra faktor lig med?b. For at brøken ikke skal ændre sig, er det nødvendigt at gange både tælleren og nævneren: a/?b ? (a ?b)/b. Eksempel 1: 10/?3 ? (10?3)/3.

3. Tilstedeværelse under stregen brøker rod brøkkraft af formen m/n, og n>mDette udtryk ser således ud: a/?(b^m/n).

4. Slip af med lignende irrationalitet også ved at indtaste en multiplikator, denne gang sværere: b^(n-m)/n, dvs. fra eksponenten af ​​selve roden er det nødvendigt at trække graden af ​​udtrykket under dets fortegn. Så vil kun den første potens blive tilbage i nævneren: a/(b^m/n) ? a ?(b^(n-m)/n)/b. Eksempel 2: 5/(4^3/5) ? 5 ?(4^2/5)/4 = 5 ?(16^1/5)/4.

5. Sum kvadratrødder Multiplicer begge komponenter brøker med en lignende forskel. Derefter, fra den irrationelle tilføjelse af rødder, omdannes nævneren til forskellen af ​​udtryk/tal under rodtegnet: a/(?b + ?c) ? a (?b - ?c)/(b - c). Eksempel 3: 9/(?13 + ?23) ? 9 (<13 - <23)/(13 - 23) = 9 (<23 - <13)/10.

6. Sum/forskel af terningrødder Vælg som en ekstra faktor det ufuldstændige kvadrat af forskellen, hvis nævneren indeholder en sum, og følgelig det ufuldstændige kvadrat af summen for forskellen mellem rødderne: a/(?b ± ?c) ? a (ab? c?)/(b ± c). Eksempel 4: 7/(?5 + ?4) ? 7 (?25-?20 +?16)/9.

7. Hvis problemet indeholder både kvadrat- og terningrødder, så opdel løsningen i to trin: udled trinvist fra nævneren Kvadrat rod, og derefter kubik. Dette gøres i henhold til de metoder, du allerede kender: i den første handling skal du vælge multiplikatoren af ​​forskellen/summen af ​​rødderne, i den anden - det ufuldstændige kvadrat af summen/forskellen.

Tip 2: Sådan slipper du af med irrationalitet i nævneren

Korrekt indtastning brøktal indeholder ikke irrationalitet V nævner. En sådan notation er lettere at forstå i udseende, derfor hvornår irrationalitet V nævner Det er smart at slippe af med det. I dette tilfælde kan irrationalitet blive en tæller.

Instruktioner

1. Til at begynde med, lad os se på et primitivt eksempel - 1/sqrt(2). Kvadratroden af ​​2 er et irrationelt tal i nævner.I dette tilfælde skal du gange brøkens tæller og nævner med dens nævner. Dette vil give et rimeligt antal ind nævner. Faktisk, sqrt(2)*sqrt(2) = sqrt(4) = 2. Multiplicering af 2 identiske kvadratrødder med hinanden vil resultere i, hvad der er under alle rødderne: i I dette tilfælde- to. Som et resultat: 1/sqrt(2) = (1*sqrt(2))/(sqrt(2)*sqrt(2)) = sqrt(2)/2. Denne algoritme er også velegnet til brøker, i nævner hvor roden ganges med et rimeligt tal. Tælleren og nævneren skal i dette tilfælde ganges med roden placeret i nævner.Eksempel: 1/(2*sqrt(3)) = (1*sqrt(3))/(2*sqrt(3)*sqrt(3)) = sqrt(3)/(2*3) = sqrt( 3)/6.

2. Selvfølgelig skal noget som dette gøres hvis nævner Det er ikke kvadratroden, der findes, men f.eks. kubikroden eller en hvilken som helst anden grad. Rod ind nævner det er nødvendigt at gange med den samme rod, og tælleren ganges også med den samme rod. Så vil roden gå ind i tælleren.

3. I et vanskeligere tilfælde i nævner der er en sum eller forskel af et irrationelt og et rimeligt tal eller 2 irrationale tal. I tilfælde af summen (forskellen) af 2 kvadratrødder eller en kvadratrod og et rimeligt tal, kan du bruge den berømte formel (x+y) )(x-y) = (x^2)-(y^2). Det vil hjælpe dig af med irrationalitet V nævner. Hvis i nævner forskel, så skal du gange tælleren og nævneren med summen af ​​de samme tal, hvis summen - så med forskellen. Denne multiplicerede sum eller forskel vil blive kaldt konjugeret til udtrykket i nævner.Resultatet af dette skema er tydeligt synligt i eksemplet: 1/(sqrt(2)+1) = (sqrt(2)-1)/(sqrt(2)+1)(sqrt(2)-1) = (sqrt(2)-1)/((sqrt(2)^2)-(1^2)) = (sqrt(2)-1)/(2-1) = sqrt(2)-1.

4. Hvis i nævner der er en sum (forskel), hvori roden er til stede i højere grad, så bliver situationen ikke-triviel og befrielse fra irrationalitet V nævner ikke altid acceptabelt

Tip 3: Sådan frigør du dig selv fra irrationalitet i nævneren af ​​en brøk

En brøk består af en tæller, placeret øverst på linjen, og en nævner, den den deler, placeret nederst. Et irrationelt tal er et tal, der ikke kan repræsenteres i formen brøker med et heltal i tælleren og et naturligt tal i nævner. Sådanne tal er f.eks. kvadratroden af ​​2 eller pi. Traditionelt, når man taler om irrationalitet i nævner, roden er underforstået.

Instruktioner

1. Fjern irrationalitet ved at gange med nævneren. På denne måde vil irrationaliteten blive overført til tælleren. Når tæller og nævner ganges med det samme tal, værdien brøkerændres ikke. Brug denne mulighed, hvis hver nævner er en rod.

2. Gang tælleren og nævneren med nævneren det nødvendige antal gange, afhængigt af roden. Hvis roden er kvadratisk, så én gang.

3. Overvej kvadratrodseksemplet. Tag brøken (56-y)/√(x+2). Den har en tæller (56-y) og en irrationel nævner √(x+2), som er kvadratroden.

4. Gang tæller og nævner brøker til nævneren, det vil sige til √(x+2). Det originale eksempel (56-y)/√(x+2) bliver ((56-y)*√(x+2))/(√(x+2)*√(x+2)). Resultatet bliver ((56-y)*√(x+2))/(x+2). Nu er roden i tælleren og inde nævner der er ingen irrationalitet.

5. Ikke altid nævneren brøker hver enkelt er under roden. Slip af med irrationalitet ved at bruge formlen (x+y)*(x-y)=x²-y².

6. Betragt eksemplet med brøken (56-y)/(√(x+2)-√y). Dens irrationelle nævner indeholder forskellen på 2 kvadratrødder. Udfyld nævneren for at danne (x+y)*(x-y).

7. Gang nævneren med summen af ​​rødderne. Gang tælleren med det samme for at få værdien brøker har ikke ændret sig. Brøken vil have formen ((56-y)*(√(x+2)+√y))/((√(x+2)-√y)*(√(x+2)+√y) ).

8. Udnyt ovenstående egenskab (x+y)*(x-y)=x²-y² og frigør nævneren fra irrationalitet. Resultatet bliver ((56-y)*(√(x+2)+√y))/(x+2-y). Nu er roden i tælleren, og nævneren er sluppet af med irrationaliteten.

9. I svære sager gentag begge disse muligheder, og anvend efter behov. Bemærk, at det ikke altid er muligt at slippe af med irrationalitet i nævner .

En algebraisk brøk er et udtryk for formen A/B, hvor bogstaverne A og B står for enhver numerisk eller bogstavelige udtryk. Ofte har tælleren og nævneren i algebraiske brøker en massiv form, men operationer med sådanne brøker skal udføres efter de samme regler som handlinger med almindelige, hvor tæller og nævner er positive heltal.

Instruktioner

1. Hvis det gives blandet brøker, omregn dem til uregelmæssige brøker (en brøk, hvor tælleren er større end nævneren): gang nævneren med hele delen, og læg tælleren sammen. Så tallet 2 1/3 bliver til 7/3. For at gøre dette skal du gange 3 med 2 og tilføje en.

2. Hvis du skal konvertere en decimal til en uægte brøk, så tænk på det som at dividere et tal uden decimal med én med lige så mange nuller, som der er tal efter decimalkommaet. Lad os forestille os, at tallet 2,5 er 25/10 (hvis du forkorter det, får du 5/2), og tallet 3,61 er 361/100. At arbejde med uægte brøker er ofte nemmere end med blandede brøker eller decimalbrøker.

3. Hvis brøker har identiske nævnere, og du skal tilføje dem, skal du blot tilføje tællere; nævnerne forbliver uændrede.

4. Hvis du skal trække brøker fra med identiske nævnere, skal du trække tælleren for den 2. brøk fra tælleren i den første brøk. Nævnerne ændrer sig heller ikke.

5. Hvis du skal tilføje brøker eller trække en brøk fra en anden, og de har forskellige nævnere, skal du reducere brøkerne til en fællesnævner. For at gøre dette skal du finde et tal, der vil være det mindste universelle multiplum (LCM) af begge nævnere eller flere, hvis brøkerne er større end 2. LCM er et tal, der vil blive opdelt i nævnerne for alle givne brøker. For eksempel, for 2 og 5 er dette tal 10.

6. Efter lighedstegnet skal du tegne en vandret linje og skrive dette tal (NOC) i nævneren. Tilføj yderligere faktorer til hele termen - det tal, som du skal gange både tælleren og nævneren med for at få LCM. Multiplicer tællerne trin for trin med yderligere faktorer, og bevar tegnet for addition eller subtraktion.

7. Beregn totalen, reducer den om nødvendigt, eller vælg hele delen. Skal du for eksempel folde den? Og?. LCM for begge brøker er 12. Så er den ekstra faktor for den første brøk 4, for 2. brøk - 3. I alt: ?+?=(1·4+1·3)/12=7/12.

8. Hvis der gives et eksempel til multiplikation, skal du gange tællerne sammen (dette vil være tælleren for totalen) og nævnerne (dette vil være nævneren af ​​totalen). I dette tilfælde er der ingen grund til at reducere dem til en fællesnævner.

9. For at dividere en brøk med en brøk, skal du vende den anden brøk på hovedet og gange brøkerne. Det vil sige a/b: c/d = a/b · d/c.

10. Faktor tæller og nævner efter behov. Flyt for eksempel universalfaktoren ud af parentesen eller udvid den efter forkortede multiplikationsformler, så du herefter om nødvendigt kan reducere tælleren og nævneren med GCD - den mindste universelle divisor.

Bemærk!
Tilføj tal med tal, bogstaver af samme slags med bogstaver af samme slags. Lad os sige, at det er umuligt at tilføje 3a og 4b, hvilket betyder, at deres sum eller forskel forbliver i tælleren - 3a±4b.

I hverdagen er falske tal mere almindelige: 1, 2, 3, 4 osv. (5 kg kartofler) og brøktal, ikke-heltal (5,4 kg løg). Mange af dem præsenteres i form decimaler. Men repræsentere decimalbrøken i form brøker ret nemt.

Instruktioner

1. Lad os sige, at tallet "0,12" er givet. Hvis du ikke reducerer denne decimalbrøk og præsenterer den som den er, så ser den sådan ud: 12/100 ("tolv hundrededele"). For at slippe af med hundrede i nævneren skal du dividere både tælleren og nævneren med et tal, der deler dem i heltal. Dette tal er 4. Ved at dividere tælleren og nævneren får vi tallet: 3/25.

2. Hvis vi ser mere på hverdagen, kan vi ofte se på prisskiltet på produkter, at dets vægt for eksempel er 0,478 kg eller lignende.. Dette tal er også let at forestille sig i form brøker:478/1000 = 239/500. Denne brøk er ret grim, og hvis der var en sandsynlighed, så ville denne decimalbrøk få lov til at blive reduceret yderligere. Og alt sammen på samme måde: at vælge et tal, der deler både tælleren og nævneren. Dette tal kaldes den største universelle faktor. Faktoren er navngivet "størst", fordi det er meget mere bekvemt umiddelbart at dividere både tælleren og nævneren med 4 (som i det første eksempel) end at dividere det to gange med 2.

Video om emnet

Decimal brøkdel- bred vifte brøker, som har et "rundt" tal i nævneren: 10, 100, 1000 osv., Sig, brøkdel 5/10 har en decimalnotation på 0,5. Med udgangspunkt i denne afhandling, brøkdel kan repræsenteres som en decimal brøker .

Instruktioner

1. Muligt, skal repræsenteres som en decimal brøkdel 18/25 Først skal du sikre dig, at et af de "runde" tal vises i nævneren: 100, 1000 osv. For at gøre dette skal du gange nævneren med 4. Men du skal gange både tælleren og nævneren med 4.

2. Multiplikation af tæller og nævner brøker 18/25 med 4, viser det sig 72/100. Dette er optaget brøkdel i decimalform: 0,72.

Når man dividerer 2 decimalbrøker, når der ikke er nogen lommeregner ved hånden, oplever mange nogle vanskeligheder. Der er virkelig ikke noget svært her. Decimal brøker kaldes sådan, hvis deres nævner har et tal, der er et multiplum af 10. Som sædvanligt skrives sådanne tal på én linje og har et komma, der adskiller brøkdelen fra helheden. Tilsyneladende på grund af tilstedeværelsen af ​​en brøkdel, som også adskiller sig i antallet af cifre efter decimalkommaet, er det ikke klart for mange, hvordan man udfører matematiske operationer med sådanne tal uden en lommeregner.

Du får brug for

• ark papir, blyant

Instruktioner

1. Det viser sig, at for at dividere en decimalbrøk med en anden, skal du se på begge tal og bestemme, hvilken af ​​dem der har flere cifre efter decimalkommaet. Vi ganger begge tal med et tal, der er et multiplum af 10, dvs. 10, 1000 eller 100000, hvor antallet af nuller er lig med mere cifre senere end decimaltegnet for et af vores 2 begyndelsestal. Nu er begge decimaler brøker omdannet til almindelige heltal. Tag et ark papir med en blyant og adskil de to resulterende tal med et "hjørne". Vi får resultatet.

2. Lad os sige, at vi skal dividere tallet 7,456 med 0,43. Det første tal har flere decimaler (3 decimaler), derfor ganger vi begge tal ikke med 1000 og får to primitive heltal: 7456 og 430. Nu dividerer vi 7456 med 430 med et "hjørne", og det får vi, hvis 7,456 divideres ved 0.43 vil den udkomme cirka 17.3.

3. Der er en anden opdelingsmetode. Nedskrivning af decimaler brøker i form af primitive brøker med tæller og nævner, for vores tilfælde er disse 7456/1000 og 43/100. Senere nedskriver vi udtrykket for at dividere 2 primitive brøker: 7456*100/1000*43, derefter reducerer vi tierne, får vi: 7456/10*43 = 7456/430 I det endelige output får vi igen divisionen af 2 primitive tal 7456 og 430, hvilket kan gøres med et “hjørne”.

Video om emnet

Nyttige råd
Måden at dividere decimalbrøker på er således at reducere dem til hele tal med støtte til at gange hver af dem med det samme tal. At udføre operationer med heltal, som sædvanligt, forårsager ingen vanskeligheder for nogen.

Video om emnet

Når man transformerer et brøkalgebraisk udtryk, hvis nævner indeholder et irrationelt udtryk, forsøger man normalt at repræsentere brøken, så dens nævner er rationel. Hvis A,B,C,D,... er nogle algebraiske udtryk, så kan du specificere regler, ved hjælp af hvilke du kan slippe af med radikale tegn i nævneren af ​​udtryk for formen

I alle disse tilfælde opnås befrielse fra irrationalitet ved at gange brøkens tæller og nævner med en faktor valgt, således at dens produkt med nævneren af ​​brøken er rationel.

1) At slippe af med irrationalitet i nævneren af ​​en brøkdel af formen . I ganges tælleren og nævneren med

Eksempel 1. .

2) Ved brøkdele af formen . Gang tælleren og nævneren med en irrationel faktor

henholdsvis til det konjugerede irrationelle udtryk.

Betydningen af ​​den sidste handling er, at i nævneren omdannes produktet af summen og forskellen til en forskel af kvadrater, som allerede vil være et rationelt udtryk.

Eksempel 2. Frigør dig fra irrationalitet i udtrykkets nævner:

Løsning, a) Gang tælleren og nævneren af ​​brøken med udtrykket . Vi får (forudsat at)

3) Ved udtryk som

nævneren behandles som en sum (forskel) og ganges med partialkvadraten af ​​forskellen (sum) for at opnå summen (forskellen) af terninger ((20.11), (20.12)). Tælleren ganges også med den samme faktor.

Eksempel 3. Befri dig selv for irrationalitet i udtryksnævneren:

Løsning, a) Betragt nævneren af ​​denne brøk som summen af ​​tallene og 1, multiplicer tælleren og nævneren med det partielle kvadrat af forskellen mellem disse tal:

eller til sidst:

I nogle tilfælde er det nødvendigt at udføre en transformation af den modsatte karakter: at frigøre brøken fra irrationalitet i tælleren. Det udføres på nøjagtig samme måde.

Eksempel 4. Befri dig selv for irrationalitet i tælleren af ​​en brøk.

Lektion nr. 1 Lektionens emne: "Befrielse fra irrationalitet i nævneren af ​​en brøk"

Mål:

Uddannelsesmæssigt:

Udviklingsmæssigt:

Uddannelsesmæssigt: skabe sammenhæng i dine handlinger.

Lektionstype: lære nye ting

Lektionsstandard:

være i stand til at finde en måde at slippe af med irrationalitet

forstå betydningen af ​​"konjugeret udtryk"

kunne slippe af med irrationalitet i nævneren.

Udstyr: kort til selvstændigt arbejde.

Under timerne

Ved du, hvordan man udvinder rødder? - spørger læreren

Ja sikkert. Du skal trække plantestammen hårdere, og dens rod vil blive fjernet fra jorden.

Nej, jeg mente en anden rod, for eksempel fra ni.

Det vil være "ni", da "th" er et suffiks.

Jeg mener kvadratrod.

Der er ingen kvadratrødder. De er fibrøse og stavformede.

Aritmetisk kvadratrod af ni.

Det ville de sige! Kvadratroden af ​​ni = 3!

Ved du, hvordan man udvinder rødder?

2. "Gentagelse er læringens moder."

(8 min)

2.Tjekker huset/huset№ 168 1)4; 2)10; 3)4;4) 8

3.Varm op. Følg trinene (slide 1). Tjek i en cirkel mod uret.

1. Vælg en ukendt faktor (Slide2)

Inddeling i grupper: efter udvalgte figurer.

Tjek ind parvis af erstatningssammensætning.

De arbejder individuelt og tjekker, vurderer point.

(Bilag 1)

3. "En bog er en bog, men brug din hjerne" (5 minutter)

(Slide 3) To venner løste en ligning
og fik forskellige svar. En af dem valgte x = , gjorde et tjek. Den anden fandt den ukendte faktor ved at dividere produktet med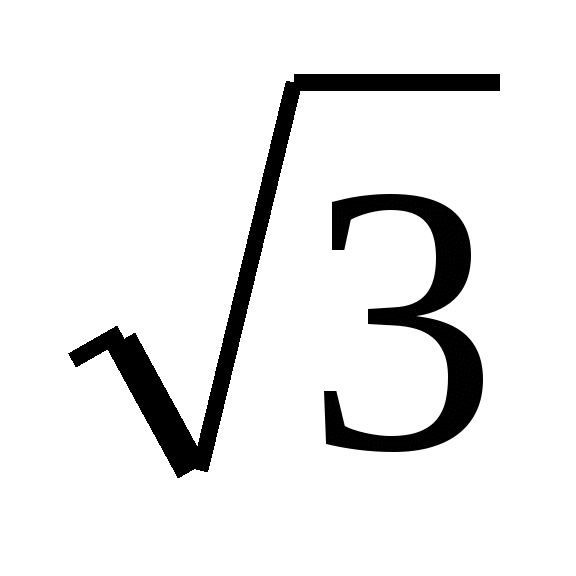
og fik x = 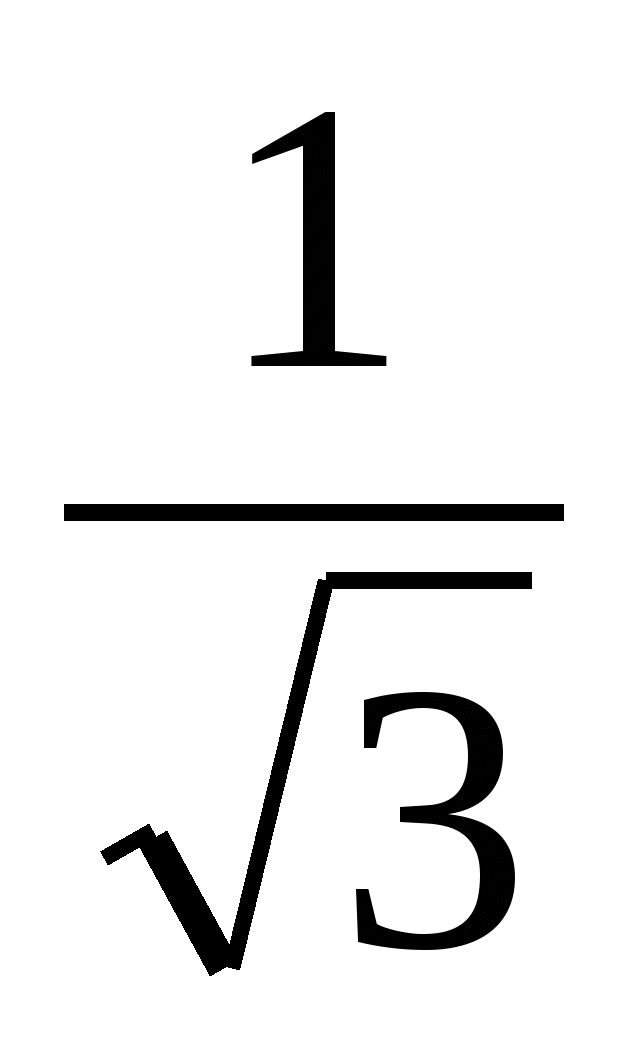. Hvilken er rigtig? Kan lineær ligning har to rødder? Det mest bekvemme udtryk for beregninger er et, der ikke indeholder irrationalitet i nævneren.

Lektionens emne(Dias 4) : Befrielse fra irrationalitet i nævneren af ​​en brøk

Mål(Dias 5) : blive fortrolig med måder at slippe af med irrationalitet i nævnerne af en brøk. Udvikling af evnen til at frigøre nævneren fra irrationalitet;

Løs og check ind parvis af skift.

De diskuterer situationen og kommer til en konklusion.

Skriv emnet ned

Formuler mål: blive fortrolig med måder at slippe af med irrationalitet i nævnerne af en brøk.

at udvikle evnen til at bestemme måden at befri dig selv fra irrationalitet;

4. Arbejde med nyt materiale.

(10 min)

Hvordan slippe af med irrationalitet i nævneren? Vil du gerne vide?

Arbejde i grupper med nyt materiale

Gruppens præstation

Fastgøring (dias 6)

De arbejder med en understøttende oversigt. (Bilag 2)

Løs eksempler.

(Bilag 3)

Udveksle oplysninger.

5. Opladning (3 min)

laver øvelser

6. Selvstændigt arbejde

(10 min)

Med kort på flere niveauer

1-in:

2-in:

3-in:

Udfør individuelt, tjek ved at udveksle notesbøger med en anden gruppe.

Pointene indtastes i gruppens scorekort.

(Bilag 1)

7.Kreativ opgave

(2 minutter)

Abe - orange sælger (dias 7)

Efter at have ankommet til min dacha engang,

Der fandt jeg et problem med de radikale.

Hun begyndte at smide dem over det hele.

Vi beder jer, piger og drenge,

Løs problemet på abens hale.

Tror du, vi er færdige med at studere dette emne? Lad os fortsætte i næste lektion.

De taler om, hvad de vil lære om dette i den næste lektion.

8. Hjemmearbejde: (2 minutter)

S.19 (dias 7)

Niveau 1: Nr. 170 (1-6)

Niveau 2: Nr. 170 (1-6 og 9.12)

Kreativ opgave: Martyshkins opgave.

Skriv ned

9. Lektionsresumé. Afspejling

(3 min)

To stjerner og et ønske på klistermærker er knyttet til det valgte humørikon (Slide 7)

Pointene omregnes til en karakter og et gruppescorekort gives til læreren.

BILAG 1

Gruppescorekort.

0-8 point

Vælg en multiplikator

0-8 point

Arbejde i gruppe med nyt materiale

0-5 point

Mig selv. Job

0-5 point

Lektionsaktivitet

0-5 point

BILAG 2

Understøttende noter

Hvis nævneren algebraisk brøk indeholder et kvadratrodstegn, så siges nævneren at indeholde irrationalitet. At omdanne et udtryk til en sådan form, at der ikke er kvadratrodstegn i brøkens nævner kaldes befrielse fra irrationalitet i nævneren

I dette emne vil vi overveje alle tre grupper af grænser med irrationalitet anført ovenfor. Lad os starte med grænser, der indeholder usikkerhed af formen $\frac(0)(0)$.

Usikkerhedsoplysning $\frac(0)(0)$.

Løsningsdiagram standard eksempler Denne type består normalt af to trin:

• Vi slipper af med den irrationalitet, der forårsagede usikkerhed, ved at gange med det såkaldte "konjugerede" udtryk;
• Indregn om nødvendigt udtrykket i tælleren eller nævneren (eller begge dele);
• Vi reducerer de faktorer, der fører til usikkerhed, og beregner den ønskede værdi af grænsen.

Udtrykket "konjugeret udtryk" anvendt ovenfor vil blive forklaret i detaljer i eksemplerne. For nu er der ingen grund til at dvæle ved det i detaljer. Generelt kan du gå den anden vej uden at bruge det konjugerede udtryk. Nogle gange kan en velvalgt erstatning eliminere irrationalitet. Sådanne eksempler er sjældne i standard tests, derfor vil vi for brugen af ​​erstatning kun overveje ét eksempel nr. 6 (se anden del af dette emne).

Vi skal bruge flere formler, som jeg vil skrive ned nedenfor:

\begin(ligning) a^2-b^2=(a-b)\cdot(a+b) \end(ligning) \begin(ligning) a^3-b^3=(a-b)\cdot(a^2 +ab+b^2) \end(ligning) \begin(ligning) a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end(ligning) \begin (ligning) a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end(ligning)

Derudover antager vi, at læseren kender formlerne til løsning af andengradsligninger. Hvis $x_1$ og $x_2$ er rødder kvadratisk trinomium$ax^2+bx+c$, så kan det faktoriseres ved hjælp af følgende formel:

\begin(ligning) ax^2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end(ligning)

Formlerne (1)-(5) er ganske tilstrækkelige til at løse standardproblemer, som vi nu går videre til.

Eksempel nr. 1

Find $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)$.

Siden $\lim_(x\to 3)(\sqrt(7-x)-2)=\sqrt(7-3)-2=\sqrt(4)-2=0$ og $\lim_(x\ til 3) (x-3)=3-3=0$, så har vi i den givne grænse en usikkerhed på formen $\frac(0)(0)$. Forskellen $\sqrt(7-x)-2$ forhindrer os i at afsløre denne usikkerhed. For at slippe af med sådanne irrationaliteter bruges multiplikation med det såkaldte "konjugerede udtryk". Vi vil nu se på, hvordan en sådan multiplikation fungerer. Multiplicer $\sqrt(7-x)-2$ med $\sqrt(7-x)+2$:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)$$

For at åbne parenteserne skal du anvende , og erstatte $a=\sqrt(7-x)$, $b=2$ i højre side af den nævnte formel:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)=(\sqrt(7-x))^2-2^2=7-x-4=3-x .$$

Som du kan se, hvis du multiplicerer tælleren med $\sqrt(7-x)+2$, så forsvinder roden (dvs. irrationalitet) i tælleren. Dette udtryk $\sqrt(7-x)+2$ vil være konjugat til udtrykket $\sqrt(7-x)-2$. Vi kan dog ikke bare gange tælleren med $\sqrt(7-x)+2$, fordi dette vil ændre brøken $\frac(\sqrt(7-x)-2)(x-3)$, som er under grænsen. Du skal gange både tælleren og nævneren på samme tid:

$$ \lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)= \venstre|\frac(0)(0)\right|=\lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt(7-x)+2)) $$

Husk nu at $(\sqrt(7-x)-2)(\sqrt(7-x)+2)=3-x$ og åbn parenteserne. Og efter at have åbnet parenteserne og en lille transformation $3-x=-(x-3)$ reducerer vi brøken med $x-3$:

$$ \lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt( 7-x)+2))= \lim_(x\til 3)\frac(3-x)((x-3)\cdot(\sqrt(7-x)+2))=\\ =\lim_ (x\to 3)\frac(-(x-3))((x-3)\cdot(\sqrt(7-x)+2))= \lim_(x\to 3)\frac(-1) )(\sqrt(7-x)+2) $$

Usikkerheden $\frac(0)(0)$ er forsvundet. Nu kan du nemt få svaret på dette eksempel:

$$ \lim_(x\to 3)\frac(-1)(\sqrt(7-x)+2)=\frac(-1)(\sqrt(7-3)+2)=-\frac( 1)(\sqrt(4)+2)=-\frac(1)(4).$$

Jeg bemærker, at det konjugerede udtryk kan ændre sin struktur, afhængigt af hvilken slags irrationalitet det skal fjerne. I eksempel nr. 4 og nr. 5 (se anden del af dette emne) vil en anden type konjugatekspression blive brugt.

Svar: $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)=-\frac(1)(4)$.

Eksempel nr. 2

Find $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$.

Siden $\lim_(x\to 2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\sqrt(2^2+5)-\sqrt(7\cdot 2 ^ 2-19)=3-3=0$ og $\lim_(x\to 2)(3x^2-5x-2)=3\cdot2^2-5\cdot 2-2=0$, så vi beskæftiger sig med usikkerhed af formen $\frac(0)(0)$. Lad os slippe af med irrationaliteten i nævneren af ​​denne brøk. For at gøre dette tilføjer vi både tælleren og nævneren af ​​brøken $\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$ til udtryk $\sqrt(x^ 2+5)+\sqrt(7x^2-19)$ konjugerer til nævneren:

$$ \lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\venstre|\frac(0 )(0)\right|= \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))) ((\sqrt(x^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))) $$

Igen, som i eksempel nr. 1, skal du bruge parenteser for at udvide. Ved at erstatte $a=\sqrt(x^2+5)$, $b=\sqrt(7x^2-19)$ i højre side af den nævnte formel, får vi følgende udtryk for nævneren:

$$ \left(\sqrt(x^2+5)-\sqrt(7x^2-19)\right)\left(\sqrt(x^2+5)+\sqrt(7x^2-19)\ højre)=\\ =\venstre(\sqrt(x^2+5)\højre)^2-\venstre(\sqrt(7x^2-19)\right)^2=x^2+5-(7x ^2-19)=-6x^2+24=-6\cdot(x^2-4) $$

Lad os vende tilbage til vores grænse:

$$ \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))((\sqrt(x) ^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19)))= \lim_(x\to 2)\frac( (3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))(-6\cdot(x^2-4))=\\ =-\ frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x^2-4) $$

I eksempel nr. 1, næsten umiddelbart efter multiplikation med konjugatekspressionen, blev fraktionen reduceret. Her, før reduktionen, skal du faktorisere udtrykkene $3x^2-5x-2$ og $x^2-4$, og først derefter gå videre til reduktionen. For at faktorisere udtrykket $3x^2-5x-2$ skal du bruge . Lad os først bestemme andengradsligning$3x^2-5x-2=0$:

$$ 3x^2-5x-2=0\\ \begin(aligned) & D=(-5)^2-4\cdot3\cdot(-2)=25+24=49;\\ & x_1=\ frac(-(-5)-\sqrt(49))(2\cdot3)=\frac(5-7)(6)=-\frac(2)(6)=-\frac(1)(3) ;\\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot3)=\frac(5+7)(6)=\frac(12)(6)=2. \end(justeret) $$

Ved at erstatte $x_1=-\frac(1)(3)$, $x_2=2$ i , vil vi have:

$$ 3x^2-5x-2=3\cdot\venstre(x-\venstre(-\frac(1)(3)\højre)\højre)(x-2)=3\cdot\venstre(x+\ frac(1)(3)\højre)(x-2)=\venstre(3\cdot x+3\cdot\frac(1)(3)\right)(x-2) =(3x+1)( x-2). $$

Nu er det tid til at faktorisere udtrykket $x^2-4$. Lad os bruge , og erstatte $a=x$, $b=2$ i det:

$$ x^2-4=x^2-2^2=(x-2)(x+2) $$

Lad os bruge de opnåede resultater. Siden $x^2-4=(x-2)(x+2)$ og $3x^2-5x-2=(3x+1)(x-2)$, så:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2) -19)))(x^2-4) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x) ^2+5)+\sqrt(7x^2-19)))((x-2)(x+2)) $$

Ved at reducere med parentesen $x-2$ får vi:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x^2+5)+\sqrt(7x^ 2-19)))((x-2)(x+2)) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt( x^2+5)+\sqrt(7x^2-19)))(x+2). $$

Alle! Uvisheden er forsvundet. Et skridt mere og vi kommer til svaret:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x+2)=\\ =-\frac(1)(6)\cdot\frac((3\cdot 2+1)(\sqrt(2^2+5)+\sqrt(7\cdot 2) ^2-19)))(2+2)= -\frac(1)(6)\cdot\frac(7(3+3))(4)=-\frac(7)(4). $$

Svar: $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=-\frac(7)( 4)$.

I det følgende eksempel skal du overveje det tilfælde, hvor irrationaliteter vil være til stede i både tælleren og nævneren af ​​brøken.

Eksempel nr. 3

Find $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9) ))$.

Siden $\lim_(x\to 5)(\sqrt(x+4)-\sqrt(x^2-16))=\sqrt(9)-\sqrt(9)=0$ og $\lim_( x \to 5)(\sqrt(x^2-3x+6)-\sqrt(5x-9))=\sqrt(16)-\sqrt(16)=0$, så har vi en usikkerhed på formen $ \frac (0)(0)$. Da rødderne i dette tilfælde er til stede i både nævneren og tælleren, er du nødt til at gange med to parenteser på én gang for at slippe af med usikkerhed. Først konjugerer udtrykket $\sqrt(x+4)+\sqrt(x^2-16)$ til tælleren. Og for det andet, til udtrykket $\sqrt(x^2-3x+6)-\sqrt(5x-9)$ konjugeret med nævneren.

$$ \lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9) ))=\venstre|\frac(0)(0)\right|=\\ =\lim_(x\til 5)\frac((\sqrt(x+4)-\sqrt(x^2-16) )(\sqrt(x+4)+\sqrt(x^2-16))(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((\sqrt(x^2) -3x+6)-\sqrt(5x-9))(\sqrt(x^2-3x+6)+\sqrt(5x-9))(\sqrt(x+4)+\sqrt(x^2) -16))) $$ $$ -x^2+x+20=0;\\ \begin(aligned) & D=1^2-4\cdot(-1)\cdot 20=81;\\ & x_1=\frac(-1-\sqrt(81))(-2)=\frac(-10)(-2)=5;\\ & x_2=\frac(-1+\sqrt(81))( -2)=\frac(8)(-2)=-4. \end(justeret) \\ -x^2+x+20=-1\cdot(x-5)(x-(-4))=-(x-5)(x+4). $$

For udtrykket $x^2-8x+15$ får vi:

$$ x^2-8x+15=0;\\ \begin(aligned) & D=(-8)^2-4\cdot 1\cdot 15=4;\\ & x_1=\frac(-(- 8)-\sqrt(4))(2)=\frac(6)(2)=3;\\ & x_2=\frac(-(-8)+\sqrt(4))(2)=\frac (10)(2)=5. \end(justed)\\ x^2+8x+15=1\cdot(x-3)(x-5)=(x-3)(x-5). $$

Udskiftning af de resulterende udvidelser $-x^2+x+20=-(x-5)(x+4)$ og $x^2+8x+15=(x-3)(x-5)$ i grænsen under overvejelse, vil have:

$$ \lim_(x\to 5)\frac((-x^2+x+20)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x^2) -8x+15)(\sqrt(x+4)+\sqrt(x^2-16)))= \lim_(x\til 5)\frac(-(x-5)(x+4)(\ sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3)(x-5)(\sqrt(x+4)+\sqrt(x^2-16)) )=\\ =\lim_(x\til 5)\frac(-(x+4)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3) (\sqrt(x+4)+\sqrt(x^2-16)))= \frac(-(5+4)(\sqrt(5^2-3\cdot 5+6)+\sqrt(5) \cdot 5-9)))((5-3)(\sqrt(5+4)+\sqrt(5^2-16)))=-6. $$

Svar: $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9) ))=-6$.

I den næste (anden) del vil vi overveje et par flere eksempler, hvor det konjugerede udtryk vil have en anden form end i de foregående opgaver. Det vigtigste at huske er, at formålet med at bruge et konjugeret udtryk er at slippe af med den irrationalitet, der forårsager usikkerhed.

På din anmodning!

5. Løs uligheden:

6 . Forenkle udtrykket:

17. f(x)=6x2 +8x+5, F(-1)=3. Find F(-2).

Lad os finde C, vel vidende at F(-1) = 3.

3 = 2 ∙ (-1) 3 + 4 ∙ (-1) 2 + 5 ∙ (-1) + C;

3 = -2 + 4 - 5 + C;

Således er antiderivatet F(x) = 2x 3 + 4x 2 + 5x + 6. Lad os finde F(-2).

F(-2) = 2∙(-2) 3 +4∙(-2) 2 +5∙(-2)+6 = -16+16-10+6=-4.

20. Slip af med irrationalitet i nævneren

Løsningen er baseret på den grundlæggende egenskab for en brøk, som gør det muligt at gange tælleren og nævneren af ​​en brøk med det samme tal, der ikke er nul. For at slippe af med radikale tegn i nævneren af ​​en brøk, bruger de normalt forkortede multiplikationsformler. Når alt kommer til alt, hvis forskellen mellem to radikaler ganges med deres sum, så får vi forskellen på kvadraterne af rødderne, dvs. du får et udtryk uden radikale fortegn.

21. Forenkle udtrykket:

Lad os løse dette eksempel på to måder. 1) Lad os forestille os det radikale udtryk for den anden faktor i form af kvadratet af summen af ​​to udtryk, dvs. i formen (a + b) 2 . Dette vil give os mulighed for at udtrække den aritmetiske kvadratrod.

2) Lad os kvadrere den første faktor og sætte den under tegnet af den aritmetiske kvadratrod af den anden faktor.

Beslut dig på en måde, der passer dig!

22. Find (x 1 ∙y 1 +x 2 ∙y 2), hvor (x n; y n) er løsninger til ligningssystemet:

Da den aritmetiske kvadratrod kun kan tages fra et ikke-negativt tal, så acceptable værdier variabel på alle tal, der opfylder uligheden y≥0. Da produktet i systemets første ligning er lig med negativt tal, så skal følgende betingelse være opfyldt: x<0 . Lad os udtrykke x fra den første ligning og erstatte dens værdi med den anden ligning. Lad os løse den resulterende ligning for på, og find derefter værdierne x svarende til de tidligere opnåede værdier på.

23. Løs uligheden: 7sin 2 x+cos 2 x>5sinx.

Da ifølge den trigonometriske hovedidentitet: sin 2 x+cos 2 x=1, så præsentere denne ulighed i formen 6sin 2 x+ sin 2 x +cos 2 x>5sinx og anvende den vigtigste trigonometrisk identitet, får vi: 6sin 2 x+ 1>5sinx. Løsning af uligheden:

6sin 2 x-5sinx+1 >0. Lad os erstatte: sinx=y og få en kvadratisk ulighed:

6y 2 -5y+1>0. Lad os løse denne ulighed ved hjælp af intervalmetoden, idet der tages hensyn til venstre side. For at gøre dette finder vi rødderne til den komplette andengradsligning:

6y 2 -5y+1=0. Diskriminerende D=b 2 -4ac=5 2 -4∙6∙1=25-24=1. Så får vi y 1 og y 2:

24. I bunden af ​​et ret prisme ligger en regulær trekant, hvis areal er Beregn arealet af prismets sideflade, hvis dets volumen er 300 cm 3.

Lad os få et regulært trekantet prisme ABCA 1 B 1 C 1, ved hvis basis ligger den korrekte Δ ABC, dens område er kendt for os. Ved hjælp af formlen for arealet af en ligesidet trekant finder vi siden af ​​vores trekant ABC. Da volumenet af et lige prisme beregnes ved formlen V=S hoved. ∙ H, og det ved vi også, så kan vi finde H - prismets højde. Prismets sidekant vil være lig med prismets højde: AA 1 =H. Ved at kende siden af ​​basen og længden af ​​prismets sidekant, kan du finde arealet af dets laterale overflade ved hjælp af formlen: S-siden. =P grundlæggende ∙ H.

25. Der var 20 spørgsmål på skolequizzen. For hvert rigtigt svar fik deltageren 12 point, og for hvert forkert svar blev der trukket 10 point. Hvor mange rigtige svar gav en af ​​deltagerne, hvis han besvarede alle spørgsmålene og fik 86 point?

Lad deltageren give x rigtige svar. Så har han (20) forkerte svar. Ved at vide, at for hvert rigtigt svar blev han tildelt 12 point, og for hvert forkert svar blev trukket 10 point, og samtidig scorede han 86 point, vil vi lave ligningen:

12x-10·(20'er)=86;

12x-200+10x=86;

22x=286 ⇒ x=286:22 ⇒ x=13. Deltageren gav 13 rigtige svar.

Jeg ønsker, at du giver 25 rigtige svar til matematikprøven på UNT!

24. I en regulær firkantet pyramide er højden 3, sidekanten er 6. Find radius af kuglen, der er afgrænset omkring pyramiden.

Lad en kugle med centrum i punktet O 1 og radius MO 1 beskrives omkring en regulær pyramide MABCD med højde MO=3 og sidekant MA=6. Det er nødvendigt at finde radius af kuglen MO 1. Overvej ΔMAM 1, hvor siden MM 1 er kuglens diameter. Derefter ∠MAM 1 =90°. Lad os finde hypotenusen MM 1, hvis siden MA og projektionen af ​​denne side MO på hypotenusen er kendt. Husk? Højde tegnet fra toppunkt ret vinkel til hypotenusen er der et middel proportional værdi mellem fremspringene af benene på hypotenusen, og hvert ben er den gennemsnitlige proportionale værdi mellem hele hypotenusen og projektionen af ​​dette ben på hypotenusen. I denne opgave vil kun den understregede del af reglen være nyttig for os.

Vi skriver ligheden: MA 2 =MO∙MM 1. Vi erstatter vores data: 6 2 =3∙MM 1. Derfor MM1 =36:3=12. Vi fandt kuglens diameter, derfor er radius af MO 1 =6.

25. Petya er ældre end Kolya, som er ældre end Misha, Masha er ældre end Kolya, og Dasha er yngre end Petya, men ældre end Masha. Hvem er den tredjeældste?

Lad os antage: ældre betyder mere. Petya er ældre end Kolya, som er ældre end Misha Lad os skrive det sådan her: Petya>Kolya>Misha. Dasha er yngre end Petya, men ældre end Masha lad os skrive det sådan her: Masha<Даша<Петя, что будет равнозначно записи: Петя>Dasha>Masha. Fordi Masha er ældre end Kolya, så får vi: Petya>Dasha>Masha>Kolya. Og til sidst: Petya>Dasha>Masha>Kolya>Misha. Således er den tredjeældste Masha.

Jeg ønsker dig succesfuld forberedelse til UNT!