നക്ഷത്ര വാർത്ത
യുക്തിരഹിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നു. ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനും ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ തിരിച്ചറിയുന്നതിനുമുള്ള അൽഗോരിതം
റിപ്പബ്ലിക് ഓഫ് ബെലാറസിന്റെ വിദ്യാഭ്യാസ മന്ത്രാലയം
വിദ്യാഭ്യാസ സ്ഥാപനം
"ഗോമൽ സ്റ്റേറ്റ് യൂണിവേഴ്സിറ്റി
ഫ്രാൻസിസ്ക് സ്കറിനയുടെ പേരിൽ
ഗണിതശാസ്ത്ര ഫാക്കൽറ്റി
ബീജഗണിതവും ജ്യാമിതിയും വകുപ്പ്
പ്രതിരോധത്തിനായി സ്വീകരിച്ചു
തല വകുപ്പ് ഷെമെറ്റ്കോവ് എൽ.എ.
ത്രികോണമിതി സമവാക്യങ്ങൾഅസമത്വങ്ങളും
കോഴ്സ് വർക്ക്
എക്സിക്യൂട്ടർ:
M-51 ഗ്രൂപ്പിലെ വിദ്യാർത്ഥി
സെമി. ഗോർസ്കി
സയന്റിഫിക് സൂപ്പർവൈസർ Ph.D.-M.Sc.,
സീനിയർ ലക്ചറർ
വി.ജി. സഫോനോവ്
ഗോമൽ 2008
ആമുഖം
ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള അടിസ്ഥാന രീതികൾ
ഫാക്‌ടറൈസേഷൻ
ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ഗുണനത്തെ ഒരു തുകയാക്കി മാറ്റിക്കൊണ്ട് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു
ട്രിപ്പിൾ ആർഗ്യുമെന്റ് ഫോർമുലകൾ ഉപയോഗിച്ച് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു
ചില ത്രികോണമിതി ഫംഗ്ഷൻ കൊണ്ട് ഗുണിക്കുക
നിലവാരമില്ലാത്ത ത്രികോണമിതി സമവാക്യങ്ങൾ
ത്രികോണമിതി അസമത്വങ്ങൾ
വേരുകളുടെ തിരഞ്ഞെടുപ്പ്
സ്വതന്ത്ര പരിഹാരത്തിനുള്ള ചുമതലകൾ
ഉപസംഹാരം
ഉപയോഗിച്ച ഉറവിടങ്ങളുടെ പട്ടിക
പുരാതന കാലത്ത്, ജ്യോതിശാസ്ത്രം, ഭൂമി സർവേയിംഗ്, നിർമ്മാണം എന്നിവയുടെ ആവശ്യങ്ങളുമായി ബന്ധപ്പെട്ട് ത്രികോണമിതി ഉടലെടുത്തു, അതായത്, അത് പൂർണ്ണമായും ജ്യാമിതീയ സ്വഭാവമുള്ളതും പ്രധാനമായും പ്രതിനിധീകരിക്കപ്പെട്ടതുമാണ്.<<исчисление хорд>>. കാലക്രമേണ, ചില വിശകലന മുഹൂർത്തങ്ങൾ അതിൽ ഇടകലരാൻ തുടങ്ങി. പതിനെട്ടാം നൂറ്റാണ്ടിന്റെ ആദ്യ പകുതിയിൽ ഒരു മൂർച്ചയുള്ള മാറ്റം സംഭവിച്ചു, അതിനുശേഷം ത്രികോണമിതി ഒരു പുതിയ ദിശയിലേക്ക് നീങ്ങുകയും ഗണിതശാസ്ത്ര വിശകലനത്തിലേക്ക് മാറുകയും ചെയ്തു. ഈ സമയത്താണ് ത്രികോണമിതി ബന്ധങ്ങളെ പ്രവർത്തനങ്ങളായി കണക്കാക്കാൻ തുടങ്ങിയത്.
ഒരു സ്കൂൾ മാത്തമാറ്റിക്സ് കോഴ്സിലെ ഏറ്റവും ബുദ്ധിമുട്ടുള്ള വിഷയങ്ങളിലൊന്നാണ് ത്രികോണമിതി സമവാക്യങ്ങൾ. പ്ലാനിമെട്രി, സ്റ്റീരിയോമെട്രി, ജ്യോതിശാസ്ത്രം, ഭൗതികശാസ്ത്രം, മറ്റ് മേഖലകൾ എന്നിവയിലെ പ്രശ്നങ്ങൾ പരിഹരിക്കുമ്പോൾ ത്രികോണമിതി സമവാക്യങ്ങൾ ഉണ്ടാകുന്നു. ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും കേന്ദ്രീകൃത ടെസ്റ്റിംഗ് ജോലികൾക്കിടയിൽ വർഷം തോറും കാണപ്പെടുന്നു.
ത്രികോണമിതി സമവാക്യങ്ങളും ബീജഗണിത സമവാക്യങ്ങളും തമ്മിലുള്ള ഏറ്റവും പ്രധാനപ്പെട്ട വ്യത്യാസം ബീജഗണിത സമവാക്യങ്ങൾക്ക് പരിമിതമായ എണ്ണം വേരുകളുണ്ട്, അതേസമയം ത്രികോണമിതി സമവാക്യങ്ങൾ --- അനന്തം, ഇത് വേരുകളുടെ തിരഞ്ഞെടുപ്പിനെ വളരെയധികം സങ്കീർണ്ണമാക്കുന്നു. ത്രികോണമിതി സമവാക്യങ്ങളുടെ മറ്റൊരു പ്രത്യേക സവിശേഷത ഉത്തരം എഴുതുന്നതിനുള്ള അദ്വിതീയ രൂപമാണ്.
ഈ തീസിസ് ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുന്നതിനുള്ള രീതികൾക്കായി നീക്കിവച്ചിരിക്കുന്നു.
പ്രബന്ധം 6 വിഭാഗങ്ങൾ ഉൾക്കൊള്ളുന്നു.
ആദ്യ വിഭാഗം അടിസ്ഥാന സൈദ്ധാന്തിക വിവരങ്ങൾ നൽകുന്നു: ത്രികോണമിതി, വിപരീത ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ നിർവചനവും ഗുണങ്ങളും; ചില ആർഗ്യുമെന്റുകൾക്കുള്ള ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ മൂല്യങ്ങളുടെ പട്ടിക; മറ്റ് ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ അടിസ്ഥാനത്തിൽ ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ആവിഷ്‌കാരം, ത്രികോണമിതി പദപ്രയോഗങ്ങളെ രൂപാന്തരപ്പെടുത്തുന്നതിന് ഇത് വളരെ പ്രധാനമാണ്, പ്രത്യേകിച്ച് വിപരീതങ്ങൾ അടങ്ങിയവ ത്രികോണമിതി പ്രവർത്തനങ്ങൾ; സ്കൂൾ കോഴ്‌സിൽ നിന്ന് അറിയപ്പെടുന്ന അടിസ്ഥാന ത്രികോണമിതി സൂത്രവാക്യങ്ങൾക്ക് പുറമേ, വിപരീത ത്രികോണമിതി പ്രവർത്തനങ്ങൾ അടങ്ങിയ പദപ്രയോഗങ്ങൾ ലളിതമാക്കുന്ന സൂത്രവാക്യങ്ങൾ നൽകിയിരിക്കുന്നു.
രണ്ടാമത്തെ വിഭാഗം ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള അടിസ്ഥാന രീതികൾ വിവരിക്കുന്നു. പ്രാഥമിക ത്രികോണമിതി സമവാക്യങ്ങളുടെ പരിഹാരം, ഫാക്‌ടറൈസേഷൻ രീതി, ത്രികോണമിതി സമവാക്യങ്ങളെ ബീജഗണിതത്തിലേക്ക് ചുരുക്കുന്നതിനുള്ള രീതികൾ എന്നിവ പരിഗണിക്കപ്പെടുന്നു. ത്രികോണമിതി സമവാക്യങ്ങൾക്കുള്ള പരിഹാരങ്ങൾ പല തരത്തിൽ എഴുതാം എന്ന വസ്തുത കാരണം, ഈ പരിഹാരങ്ങളുടെ രൂപം ഈ പരിഹാരങ്ങൾ സമാനമാണോ വ്യത്യസ്തമാണോ എന്ന് പെട്ടെന്ന് നിർണ്ണയിക്കാൻ ഒരാളെ അനുവദിക്കുന്നില്ല.<<сбить с толку>> പരിശോധനകൾ പരിഹരിക്കുമ്പോൾ, ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പൊതു സ്കീം പരിഗണിക്കുകയും ത്രികോണമിതി സമവാക്യങ്ങളുടെ പൊതുവായ പരിഹാരങ്ങളുടെ ഗ്രൂപ്പുകളുടെ പരിവർത്തനം വിശദമായി പരിഗണിക്കുകയും ചെയ്യുന്നു.
മൂന്നാമത്തെ വിഭാഗം നിലവാരമില്ലാത്ത ത്രികോണമിതി സമവാക്യങ്ങൾ പരിശോധിക്കുന്നു, അവയുടെ പരിഹാരങ്ങൾ പ്രവർത്തനപരമായ സമീപനത്തെ അടിസ്ഥാനമാക്കിയുള്ളതാണ്.
നാലാമത്തെ ഭാഗം ത്രികോണമിതി അസമത്വങ്ങളെക്കുറിച്ച് ചർച്ച ചെയ്യുന്നു. പ്രാഥമിക പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ വിശദമായി ചർച്ചചെയ്യുന്നു. ത്രികോണമിതി അസമത്വങ്ങൾ, യൂണിറ്റ് സർക്കിളിലും ഗ്രാഫിക്കിലും. പ്രാഥമിക അസമത്വങ്ങളിലൂടെ നോൺ-എലിമെന്ററി ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്ന പ്രക്രിയയും സ്കൂൾ കുട്ടികൾക്ക് ഇതിനകം നന്നായി അറിയാവുന്ന ഇടവേളകളുടെ രീതിയും വിവരിച്ചിരിക്കുന്നു.
അഞ്ചാമത്തെ വിഭാഗം ഏറ്റവും ബുദ്ധിമുട്ടുള്ള ജോലികൾ അവതരിപ്പിക്കുന്നു: ഒരു ത്രികോണമിതി സമവാക്യം പരിഹരിക്കാൻ മാത്രമല്ല, ചില വ്യവസ്ഥകൾ നിറവേറ്റുന്ന കണ്ടെത്തിയ വേരുകളിൽ നിന്ന് വേരുകൾ തിരഞ്ഞെടുക്കാനും അത് ആവശ്യമായി വരുമ്പോൾ. ഈ വിഭാഗം സാധാരണ റൂട്ട് തിരഞ്ഞെടുക്കൽ ജോലികൾക്കുള്ള പരിഹാരങ്ങൾ നൽകുന്നു. വേരുകൾ തിരഞ്ഞെടുക്കുന്നതിന് ആവശ്യമായ സൈദ്ധാന്തിക വിവരങ്ങൾ നൽകിയിരിക്കുന്നു: ഒരു കൂട്ടം പൂർണ്ണസംഖ്യകളെ വിഭജിക്കാത്ത ഉപഗണങ്ങളായി വിഭജിക്കുക, പൂർണ്ണസംഖ്യകളിലെ സമവാക്യങ്ങൾ പരിഹരിക്കുക (ഡയഫാന്റൈൻ).
ആറാമത്തെ വിഭാഗം ടാസ്‌ക്കുകൾ അവതരിപ്പിക്കുന്നു സ്വതന്ത്രമായ തീരുമാനം, ഒരു ടെസ്റ്റ് രൂപത്തിൽ രൂപകൽപ്പന ചെയ്തിരിക്കുന്നത്. 20 ടെസ്റ്റ് ടാസ്‌ക്കുകളിൽ കേന്ദ്രീകൃത പരിശോധനയ്ക്കിടെ നേരിടാൻ കഴിയുന്ന ഏറ്റവും ബുദ്ധിമുട്ടുള്ള ജോലികൾ അടങ്ങിയിരിക്കുന്നു.
പ്രാഥമിക ത്രികോണമിതി സമവാക്യങ്ങൾ
എലിമെന്ററി ത്രികോണമിതി സമവാക്യങ്ങൾ ഫോമിന്റെ സമവാക്യങ്ങളാണ്, ഇവിടെ --- ത്രികോണമിതി പ്രവർത്തനങ്ങളിൽ ഒന്ന്: , , , .
എലിമെന്ററി ത്രികോണമിതി സമവാക്യങ്ങൾക്ക് അനന്തമായ വേരുകളുണ്ട്. ഉദാഹരണത്തിന്, ഇനിപ്പറയുന്ന മൂല്യങ്ങൾ സമവാക്യത്തെ തൃപ്തിപ്പെടുത്തുന്നു: , , മുതലായവ. പൊതു ഫോർമുലസമവാക്യത്തിന്റെ എല്ലാ വേരുകളും കണ്ടെത്തുന്നിടത്ത്, എവിടെയാണ്:
ഇവിടെ ഇതിന് ഏതെങ്കിലും പൂർണ്ണസംഖ്യ മൂല്യങ്ങൾ എടുക്കാം, അവ ഓരോന്നും സമവാക്യത്തിന്റെ ഒരു പ്രത്യേക റൂട്ടിനോട് യോജിക്കുന്നു; ഈ സൂത്രവാക്യത്തിൽ (അതുപോലെ പ്രാഥമിക ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്ന മറ്റ് സൂത്രവാക്യങ്ങളിലും) വിളിക്കുന്നു പരാമീറ്റർ. അവർ സാധാരണയായി എഴുതുന്നു, അതുവഴി പാരാമീറ്ററിന് ഏതെങ്കിലും പൂർണ്ണസംഖ്യ മൂല്യങ്ങൾ സ്വീകരിക്കാൻ കഴിയുമെന്ന് ഊന്നിപ്പറയുന്നു.
സമവാക്യത്തിന്റെ പരിഹാരങ്ങൾ , എവിടെ , ഫോർമുല ഉപയോഗിച്ച് കണ്ടെത്തുന്നു
സമവാക്യം സമവാക്യം ഉപയോഗിച്ച് പരിഹരിക്കുന്നു
ഒപ്പം സമവാക്യം ഫോർമുല പ്രകാരമാണ്
പൊതുവായ സൂത്രവാക്യങ്ങൾ ഉപയോഗിക്കാതെ പരിഹാരം എഴുതാൻ കഴിയുമ്പോൾ പ്രാഥമിക ത്രികോണമിതി സമവാക്യങ്ങളുടെ ചില പ്രത്യേക കേസുകൾ നമുക്ക് പ്രത്യേകം ശ്രദ്ധിക്കാം:
ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ പ്രധാന പങ്ക്ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ കാലഘട്ടം കളിക്കുന്നു. അതിനാൽ, ഞങ്ങൾ രണ്ട് ഉപയോഗപ്രദമായ സിദ്ധാന്തങ്ങൾ അവതരിപ്പിക്കുന്നു:
സിദ്ധാന്തം --- ഫംഗ്ഷന്റെ പ്രധാന കാലയളവ് ആണെങ്കിൽ, സംഖ്യയാണ് ഫംഗ്ഷന്റെ പ്രധാന കാലയളവ്.
ഫംഗ്ഷനുകളുടെ കാലഘട്ടങ്ങളും നിലവിലുണ്ടെങ്കിൽ ആനുപാതികമാണെന്ന് പറയപ്പെടുന്നു പൂർണ്ണസംഖ്യകൾഅതുകൊണ്ട് .
സിദ്ധാന്തം ആനുകാലിക ഫംഗ്‌ഷനുകൾക്കും , ആനുപാതികവും ഒപ്പം ഉണ്ടെങ്കിൽ, അവയ്‌ക്ക് ഒരു പൊതു കാലഘട്ടമുണ്ട്, അത് ഫംഗ്ഷനുകളുടെ കാലഘട്ടമാണ്, , .
ഫംഗ്ഷന്റെ കാലയളവ് , , ആണ്, പ്രധാന കാലയളവ് അത് ആവശ്യമില്ലെന്ന് സിദ്ധാന്തം പറയുന്നു. ഉദാഹരണത്തിന്, ഫംഗ്ഷനുകളുടെ പ്രധാന കാലയളവ് കൂടാതെ --- , അവയുടെ ഉൽപ്പന്നത്തിന്റെ പ്രധാന കാലയളവ് --- .
ഒരു സഹായ വാദം അവതരിപ്പിക്കുന്നു
ഫോമിന്റെ എക്സ്പ്രഷനുകൾ രൂപാന്തരപ്പെടുത്തുന്നതിനുള്ള സ്റ്റാൻഡേർഡ് വഴി 
ഇനിപ്പറയുന്ന സാങ്കേതികതയാണ്: അനുവദിക്കുക --- മൂല, തുല്യതകൾ നൽകിയത് 
, 
. ഏതൊരു കാര്യത്തിനും, അത്തരമൊരു ആംഗിൾ നിലവിലുണ്ട്. അങ്ങനെ . എങ്കിൽ , അല്ലെങ്കിൽ , , മറ്റ് സന്ദർഭങ്ങളിൽ.
ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സ്കീം
ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ ഞങ്ങൾ പിന്തുടരുന്ന അടിസ്ഥാന സ്കീം ഇപ്രകാരമാണ്:
തന്നിരിക്കുന്ന ഒരു സമവാക്യം പരിഹരിക്കുന്നത് പ്രാഥമിക സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിലേക്ക് ചുരുക്കിയിരിക്കുന്നു. പരിഹാരങ്ങൾ --- പരിവർത്തനങ്ങൾ, ഫാക്‌ടറൈസേഷൻ, അജ്ഞാതരെ മാറ്റിസ്ഥാപിക്കൽ. നിങ്ങളുടെ വേരുകൾ നഷ്ടപ്പെടുത്തരുത് എന്നതാണ് മാർഗ്ഗനിർദ്ദേശ തത്വം. ഇതിനർത്ഥം, അടുത്ത സമവാക്യങ്ങളിലേക്ക് (കളിലേക്ക്) നീങ്ങുമ്പോൾ, അധിക (പുറം) വേരുകളുടെ രൂപത്തെ ഞങ്ങൾ ഭയപ്പെടുന്നില്ല, പക്ഷേ ഞങ്ങളുടെ “ചെയിനിന്റെ” തുടർന്നുള്ള ഓരോ സമവാക്യവും (അല്ലെങ്കിൽ ശാഖകളുടെ കാര്യത്തിൽ ഒരു കൂട്ടം സമവാക്യങ്ങൾ) ശ്രദ്ധിക്കുക. ) മുമ്പത്തേതിന്റെ അനന്തരഫലമാണ്. അതിലൊന്ന് സാധ്യമായ രീതികൾറൂട്ട് തിരഞ്ഞെടുക്കൽ ഒരു പരിശോധനയാണ്. ത്രികോണമിതി സമവാക്യങ്ങളുടെ കാര്യത്തിൽ, ബീജഗണിത സമവാക്യങ്ങളുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ, ഒരു ചട്ടം പോലെ, വേരുകൾ തിരഞ്ഞെടുക്കുന്നതിലും പരിശോധിക്കുന്നതിലും ബന്ധപ്പെട്ട ബുദ്ധിമുട്ടുകൾ കുത്തനെ വർദ്ധിക്കുമെന്ന് നമുക്ക് ഉടനടി ശ്രദ്ധിക്കാം. എല്ലാത്തിനുമുപരി, അനന്തമായ പദങ്ങൾ അടങ്ങിയ പരമ്പരകൾ ഞങ്ങൾ പരിശോധിക്കേണ്ടതുണ്ട്.
ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ അജ്ഞാതരെ മാറ്റിസ്ഥാപിക്കുന്നതിനെക്കുറിച്ച് പ്രത്യേകം പരാമർശിക്കേണ്ടതാണ്. മിക്ക കേസുകളിലും, ആവശ്യമായ പകരത്തിനു ശേഷം, ഒരു ബീജഗണിത സമവാക്യം ലഭിക്കും. മാത്രമല്ല, സമവാക്യങ്ങൾ അത്ര അപൂർവമല്ല, അവ ത്രികോണമിതിയിലാണെങ്കിലും രൂപം, അടിസ്ഥാനപരമായി അവർ അല്ല, ആദ്യ ഘട്ടത്തിന് ശേഷം --- പകരക്കാർവേരിയബിളുകൾ --- ബീജഗണിതമായി മാറുന്നു, പ്രാഥമിക ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്ന ഘട്ടത്തിൽ മാത്രമാണ് ത്രികോണമിതിയിലേക്ക് ഒരു തിരിച്ചുവരവ് സംഭവിക്കുന്നത്.
ഞങ്ങൾ നിങ്ങളെ ഒരിക്കൽ കൂടി ഓർമ്മിപ്പിക്കാം: അജ്ഞാതമായവയുടെ മാറ്റിസ്ഥാപിക്കൽ ആദ്യ അവസരത്തിൽ ചെയ്യണം; മാറ്റിസ്ഥാപിച്ചതിന് ശേഷമുള്ള ഫലമായുണ്ടാകുന്ന സമവാക്യം വേരുകൾ തിരഞ്ഞെടുക്കുന്ന ഘട്ടം ഉൾപ്പെടെ അവസാനം വരെ പരിഹരിക്കപ്പെടണം, അതിനുശേഷം മാത്രമേ യഥാർത്ഥ അജ്ഞാതത്തിലേക്ക് മടങ്ങൂ.
ത്രികോണമിതി സമവാക്യങ്ങളുടെ ഒരു സവിശേഷത, പല കേസുകളിലും ഉത്തരം എഴുതാം എന്നതാണ് വ്യത്യസ്ത വഴികൾ. സമവാക്യം പരിഹരിക്കാൻ പോലും 
ഉത്തരം ഇനിപ്പറയുന്ന രീതിയിൽ എഴുതാം:
1) രണ്ട് പരമ്പരകളുടെ രൂപത്തിൽ: 
, , ;
2) സ്റ്റാൻഡേർഡ് രൂപത്തിൽ, മുകളിൽ പറഞ്ഞ ശ്രേണിയുടെ സംയോജനമാണ്: , ;
3) കാരണം 
, അപ്പോൾ ഉത്തരം ഫോമിൽ എഴുതാം 
, (ഇനിപ്പറയുന്നവയിൽ, പ്രതികരണ റെക്കോർഡിലെ , , അല്ലെങ്കിൽ പാരാമീറ്ററിന്റെ സാന്നിധ്യം സ്വയമേവ അർത്ഥമാക്കുന്നത് ഈ പരാമീറ്റർ സാധ്യമായ എല്ലാ പൂർണ്ണസംഖ്യ മൂല്യങ്ങളും സ്വീകരിക്കുന്നു എന്നാണ്. ഒഴിവാക്കലുകൾ വ്യക്തമാക്കും.)
വ്യക്തമായും, ലിസ്റ്റുചെയ്ത മൂന്ന് കേസുകൾ പരിഗണനയിലുള്ള സമവാക്യത്തിന് ഉത്തരം എഴുതാനുള്ള എല്ലാ സാധ്യതകളും തീർന്നില്ല (അവയിൽ അനന്തമായി ധാരാളം ഉണ്ട്).
ഉദാഹരണത്തിന്, സമത്വം സത്യമാകുമ്പോൾ 
. അതിനാൽ, ആദ്യത്തെ രണ്ട് കേസുകളിൽ, എങ്കിൽ, നമുക്ക് മാറ്റിസ്ഥാപിക്കാം .
സാധാരണയായി പോയിന്റ് 2 അടിസ്ഥാനമാക്കിയാണ് ഉത്തരം എഴുതുന്നത്. ഓർക്കുന്നത് നല്ലതാണ് ഇനിപ്പറയുന്ന ശുപാർശ: സമവാക്യം പരിഹരിക്കുന്നതിൽ ജോലി അവസാനിക്കുന്നില്ലെങ്കിൽ, ഗവേഷണം നടത്തുകയും വേരുകൾ തിരഞ്ഞെടുക്കുകയും ചെയ്യേണ്ടത് ഇപ്പോഴും ആവശ്യമാണ്, തുടർന്ന് ഏറ്റവും സൗകര്യപ്രദമായ റെക്കോർഡിംഗ് രൂപം ഖണ്ഡിക 1 ൽ സൂചിപ്പിച്ചിരിക്കുന്നു. (സമവാക്യത്തിന് സമാനമായ ഒരു ശുപാർശ നൽകണം.)
പറഞ്ഞ കാര്യങ്ങൾ വ്യക്തമാക്കുന്ന ഒരു ഉദാഹരണം നോക്കാം.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ഏറ്റവും വ്യക്തമായ മാർഗം ഇനിപ്പറയുന്നതാണ്. ഈ സമവാക്യം രണ്ടായി വിഭജിക്കുന്നു: ഒപ്പം . അവ ഓരോന്നും പരിഹരിച്ച് ലഭിച്ച ഉത്തരങ്ങൾ സംയോജിപ്പിച്ച്, ഞങ്ങൾ കണ്ടെത്തുന്നു .
മറ്റൊരു വഴി.മുതൽ, ഡിഗ്രി കുറയ്ക്കുന്നതിനുള്ള ഫോർമുലകൾ മാറ്റിസ്ഥാപിക്കുകയും ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ചെറിയ പരിവർത്തനങ്ങൾക്ക് ശേഷം നമുക്ക് എവിടെ നിന്ന് ലഭിക്കും 
.
ഒറ്റനോട്ടത്തിൽ, രണ്ടാമത്തെ ഫോർമുലയ്ക്ക് ആദ്യത്തേതിനേക്കാൾ പ്രത്യേക ഗുണങ്ങളൊന്നുമില്ല. എന്നിരുന്നാലും, നമ്മൾ എടുക്കുകയാണെങ്കിൽ, ഉദാഹരണത്തിന്, അത് മാറുന്നു, അതായത്. സമവാക്യത്തിന് ഒരു പരിഹാരമുണ്ട്, ആദ്യ രീതി നമ്മെ ഉത്തരത്തിലേക്ക് നയിക്കുന്നു 
. "കാണുക" സമത്വം തെളിയിക്കുക 
അത്ര എളുപ്പമല്ല.
ഉത്തരം. .
ത്രികോണമിതി സമവാക്യങ്ങളുടെ പൊതുവായ പരിഹാരങ്ങളുടെ ഗ്രൂപ്പുകളെ പരിവർത്തനം ചെയ്യുകയും സംയോജിപ്പിക്കുകയും ചെയ്യുന്നു
ഞങ്ങൾ പരിഗണിക്കും ഗണിത പുരോഗതി, രണ്ട് ദിശകളിലേക്കും അനന്തമായി നീളുന്നു. ഈ പുരോഗതിയിലെ അംഗങ്ങളെ രണ്ട് ഗ്രൂപ്പുകളായി തിരിക്കാം, അവ ഒരു നിശ്ചിത അംഗത്തിന്റെ വലത്തോട്ടും ഇടത്തോട്ടും സ്ഥിതി ചെയ്യുന്നു, ഇത് പുരോഗതിയുടെ സെൻട്രൽ അല്ലെങ്കിൽ സീറോ അംഗം എന്ന് വിളിക്കുന്നു.
അനന്തമായ പുരോഗതിയുടെ നിബന്ധനകളിൽ ഒന്ന് പൂജ്യം സംഖ്യ ഉപയോഗിച്ച് ഉറപ്പിക്കുന്നതിലൂടെ, ശേഷിക്കുന്ന എല്ലാ നിബന്ധനകൾക്കും ഞങ്ങൾ ഇരട്ട നമ്പറിംഗ് നടത്തേണ്ടതുണ്ട്: വലതുവശത്ത് സ്ഥിതിചെയ്യുന്ന പദങ്ങൾക്ക് പോസിറ്റീവ്, പൂജ്യത്തിന്റെ ഇടതുവശത്ത് സ്ഥിതിചെയ്യുന്ന പദങ്ങൾക്ക് നെഗറ്റീവ്.
പൊതുവേ, പുരോഗതിയുടെ വ്യത്യാസം പൂജ്യം പദമാണെങ്കിൽ, അനന്തമായ ഗണിത പുരോഗതിയുടെ ഏതെങ്കിലും (th) പദത്തിന്റെ സൂത്രവാക്യം ഇതാണ്:
അനന്തമായ ഗണിത പുരോഗതിയുടെ ഏത് പദത്തിനും ഫോർമുല പരിവർത്തനങ്ങൾ
1. നിങ്ങൾ പുരോഗതിയുടെ വ്യത്യാസം പൂജ്യം പദത്തിലേക്ക് കൂട്ടിച്ചേർക്കുകയോ കുറയ്ക്കുകയോ ചെയ്താൽ, പുരോഗതി മാറില്ല, പക്ഷേ പൂജ്യം പദത്തിന് മാത്രമേ നീങ്ങൂ, അതായത്. അംഗങ്ങളുടെ എണ്ണത്തിൽ മാറ്റം വരും.
2. ഒരു വേരിയബിൾ മൂല്യത്തിന്റെ ഗുണകം ഗുണിച്ചാൽ, ഇത് അംഗങ്ങളുടെ വലത്, ഇടത് ഗ്രൂപ്പുകളുടെ പുനഃക്രമീകരണത്തിൽ മാത്രമേ കലാശിക്കൂ.
3. അനന്തമായ പുരോഗതിയുടെ തുടർച്ചയായ നിബന്ധനകളാണെങ്കിൽ
ഉദാഹരണത്തിന്, , , ..., , പുരോഗതികളുടെ കേന്ദ്ര നിബന്ധനകൾ തുല്യമായ വ്യത്യാസത്തിൽ ഉണ്ടാക്കുക:
പിന്നീട് ഒരു പുരോഗതിയും പുരോഗതികളുടെ ഒരു പരമ്പരയും ഒരേ സംഖ്യകൾ പ്രകടിപ്പിക്കുന്നു.
ഉദാഹരണം വരിയെ ഇനിപ്പറയുന്ന മൂന്ന് വരികൾ ഉപയോഗിച്ച് മാറ്റിസ്ഥാപിക്കാം: , , .
4. ഒരേ വ്യത്യാസമുള്ള അനന്തമായ പുരോഗതികൾക്ക് വ്യത്യാസമുള്ള ഒരു ഗണിത പുരോഗതി രൂപപ്പെടുത്തുന്ന കേന്ദ്ര പദങ്ങളുടെ സംഖ്യകളുണ്ടെങ്കിൽ, ഈ ശ്രേണികൾക്ക് വ്യത്യാസമുള്ള ഒരു പുരോഗതിയും ഈ പുരോഗതികളുടെ ഏതെങ്കിലും കേന്ദ്ര പദങ്ങൾക്ക് തുല്യമായ ഒരു കേന്ദ്ര പദവും ഉപയോഗിച്ച് മാറ്റിസ്ഥാപിക്കാം. അതായത് എങ്കിൽ
തുടർന്ന് ഈ പുരോഗതികൾ ഒന്നായി സംയോജിപ്പിക്കുന്നു:
ഉദാഹരണം
... രണ്ടും ഒരു ഗ്രൂപ്പായി സംയോജിപ്പിച്ചിരിക്കുന്നു, കാരണം 
.
പൊതുവായ പരിഹാരങ്ങളുള്ള ഗ്രൂപ്പുകളെ പൊതുവായ പരിഹാരങ്ങളില്ലാത്ത ഗ്രൂപ്പുകളായി പരിവർത്തനം ചെയ്യുന്നതിന്, ഈ ഗ്രൂപ്പുകളെ ഒരു പൊതു കാലയളവുള്ള ഗ്രൂപ്പുകളായി വിഘടിപ്പിക്കുന്നു, തുടർന്ന് ആവർത്തിച്ചുള്ളവ ഒഴികെയുള്ള ഗ്രൂപ്പുകളെ ഒന്നിപ്പിക്കാൻ ശ്രമിക്കുക.
ഫാക്‌ടറൈസേഷൻ
ഫാക്‌ടറൈസേഷൻ രീതി ഇപ്രകാരമാണ്: എങ്കിൽ
അപ്പോൾ സമവാക്യത്തിന്റെ ഓരോ പരിഹാരവും
ഒരു കൂട്ടം സമവാക്യങ്ങൾക്കുള്ള പരിഹാരമാണ്
വിപരീത പ്രസ്താവന, പൊതുവേ പറഞ്ഞാൽ, തെറ്റാണ്: ജനസംഖ്യയ്ക്കുള്ള എല്ലാ പരിഹാരങ്ങളും സമവാക്യത്തിനുള്ള പരിഹാരമല്ല. വ്യക്തിഗത സമവാക്യങ്ങൾക്കുള്ള പരിഹാരങ്ങൾ ഫംഗ്ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌നിൽ ഉൾപ്പെടുത്തിയേക്കില്ല എന്ന വസ്തുതയാണ് ഇത് വിശദീകരിക്കുന്നത്.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.അടിസ്ഥാനം ഉപയോഗിക്കുന്നത് ത്രികോണമിതി ഐഡന്റിറ്റി, ഫോമിലെ സമവാക്യത്തെ പ്രതിനിധീകരിക്കാം
ഉത്തരം.
; 
.
ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ ആകെത്തുക ഒരു ഉൽപ്പന്നമാക്കി മാറ്റുന്നു
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.ഫോർമുല പ്രയോഗിക്കുമ്പോൾ, നമുക്ക് തുല്യമായ സമവാക്യം ലഭിക്കും
ഉത്തരം. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം. IN ഈ സാഹചര്യത്തിൽ, ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ആകെത്തുകയ്ക്കുള്ള ഫോർമുലകൾ പ്രയോഗിക്കുന്നതിന് മുമ്പ്, നിങ്ങൾ റിഡക്ഷൻ ഫോർമുല ഉപയോഗിക്കണം 
. തൽഫലമായി, നമുക്ക് തുല്യമായ സമവാക്യം ലഭിക്കും
ഉത്തരം.
, 
.
ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ഗുണനത്തെ ഒരു തുകയാക്കി മാറ്റിക്കൊണ്ട് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു
നിരവധി സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ, സൂത്രവാക്യങ്ങൾ ഉപയോഗിക്കുന്നു.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക
പരിഹാരം.
ഉത്തരം. , .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.സമവാക്യം പ്രയോഗിക്കുമ്പോൾ, നമുക്ക് തുല്യമായ ഒരു സമവാക്യം ലഭിക്കും:
ഉത്തരം. .
റിഡക്ഷൻ ഫോർമുലകൾ ഉപയോഗിച്ച് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു
വിശാലമായ ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ, സൂത്രവാക്യങ്ങൾ ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ഫോർമുല പ്രയോഗിക്കുമ്പോൾ, നമുക്ക് തുല്യമായ ഒരു സമവാക്യം ലഭിക്കും.
ഉത്തരം. ; .
ട്രിപ്പിൾ ആർഗ്യുമെന്റ് ഫോർമുലകൾ ഉപയോഗിച്ച് സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ഫോർമുല പ്രയോഗിക്കുമ്പോൾ, നമുക്ക് സമവാക്യം ലഭിക്കും
ഉത്തരം. ; .
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.നമുക്ക് ലഭിക്കുന്ന ബിരുദം കുറയ്ക്കുന്നതിനുള്ള ഫോർമുലകൾ പ്രയോഗിക്കുന്നു: 
. അപേക്ഷിച്ചാൽ നമുക്ക് ലഭിക്കുന്നത്:
ഉത്തരം. ; .
ഒരേ പേരിലുള്ള ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ തുല്യത
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.
ഉത്തരം. , .
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.നമുക്ക് സമവാക്യം രൂപാന്തരപ്പെടുത്താം.
ഉത്തരം. .
ഉദാഹരണം അത് അറിയുകയും സമവാക്യം തൃപ്തിപ്പെടുത്തുകയും ചെയ്യുന്നു
തുക കണ്ടെത്തുക.
പരിഹാരം.സമവാക്യത്തിൽ നിന്ന് അത് പിന്തുടരുന്നു
ഉത്തരം. .
ഫോമിന്റെ തുകകൾ നമുക്ക് പരിഗണിക്കാം
ഈ തുകകളെ ഗുണിച്ചും ഹരിച്ചും ഒരു ഉൽപ്പന്നമാക്കി മാറ്റാം, അപ്പോൾ നമുക്ക് ലഭിക്കും
ചില ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കാൻ ഈ സാങ്കേതികവിദ്യ ഉപയോഗിക്കാം, പക്ഷേ അതിന്റെ ഫലമായി ബാഹ്യമായ വേരുകൾ പ്രത്യക്ഷപ്പെടാം എന്നത് മനസ്സിൽ പിടിക്കണം. നമുക്ക് ഈ സൂത്രവാക്യങ്ങൾ സംഗ്രഹിക്കാം:
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.യഥാർത്ഥ സമവാക്യത്തിനുള്ള പരിഹാരമാണ് സെറ്റ് എന്ന് കാണാൻ കഴിയും. അതിനാൽ, സമവാക്യത്തിന്റെ ഇടത് വലത് വശങ്ങൾ ഗുണിക്കുന്നത് അധിക വേരുകളുടെ രൂപത്തിലേക്ക് നയിക്കില്ല.
നമുക്ക് ഉണ്ട് 
.
ഉത്തരം. ; .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.സമവാക്യത്തിന്റെ ഇടത് വലത് വശങ്ങൾ ഗുണിച്ച് ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ഉൽപ്പന്നത്തെ ഒരു തുകയാക്കി മാറ്റുന്നതിനുള്ള സൂത്രവാക്യങ്ങൾ പ്രയോഗിക്കാം, നമുക്ക് ലഭിക്കും
ഈ സമവാക്യം രണ്ട് സമവാക്യങ്ങളുടെ സംയോജനത്തിന് തുല്യമാണ്, എവിടെ നിന്ന്, .
സമവാക്യത്തിന്റെ വേരുകൾ സമവാക്യത്തിന്റെ വേരുകളല്ലാത്തതിനാൽ, നമ്മൾ ഒഴിവാക്കണം. ഇതിനർത്ഥം സെറ്റിൽ അത് ഒഴിവാക്കേണ്ടത് ആവശ്യമാണ് എന്നാണ്.
ഉത്തരം.ഒപ്പം , .
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.നമുക്ക് പദപ്രയോഗം രൂപാന്തരപ്പെടുത്താം:
സമവാക്യം ഇങ്ങനെ എഴുതപ്പെടും:
ഉത്തരം. .
ത്രികോണമിതി സമവാക്യങ്ങളെ ബീജഗണിതത്തിലേക്ക് ചുരുക്കുന്നു
ചതുരാകൃതിയിലേക്ക് ചുരുക്കാം
സമവാക്യം രൂപത്തിലാണെങ്കിൽ
പിന്നീട് മാറ്റിസ്ഥാപിക്കുന്നത് അതിനെ സമചതുരത്തിലേക്ക് നയിക്കുന്നു 
() ഒപ്പം.
പദത്തിന് പകരം ഉണ്ടെങ്കിൽ, പിന്നെ ആവശ്യമായ മാറ്റിസ്ഥാപിക്കൽചെയ്യും .
സമവാക്യം
വരെ വരുന്നു ക്വാഡ്രാറ്റിക് സമവാക്യം
എന്ന നിലയിൽ അവതരണം 
. ഏത് സമവാക്യത്തിന്റെ വേരുകളല്ലെന്ന് പരിശോധിക്കുന്നത് എളുപ്പമാണ്, പകരം വയ്ക്കുന്നത് വഴി സമവാക്യം ഒരു ക്വാഡ്രാറ്റിക് ആയി ചുരുക്കുന്നു.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.നമുക്ക് അത് ഇടത് വശത്തേക്ക് നീക്കാം, അത് മാറ്റി പകരം വയ്ക്കാം, കൂടാതെ അതിലൂടെ പ്രകടിപ്പിക്കാം.
ലളിതവൽക്കരണത്തിന് ശേഷം നമുക്ക് ലഭിക്കുന്നത്: . ടേം കൊണ്ട് ടേം ഹരിച്ച് മാറ്റിസ്ഥാപിക്കുക:
ലേക്ക് മടങ്ങുമ്പോൾ, ഞങ്ങൾ കണ്ടെത്തുന്നു 
.
എന്നതുമായി ബന്ധപ്പെട്ട് ഏകതാനമായ സമവാക്യങ്ങൾ,
ഫോമിന്റെ ഒരു സമവാക്യം പരിഗണിക്കുക
എവിടെ,,,...,, --- സാധുവാണ്സംഖ്യകൾ. സമവാക്യത്തിന്റെ ഇടതുവശത്തുള്ള ഓരോ പദത്തിലും, മോണോമിയലുകളുടെ ഡിഗ്രികൾ തുല്യമാണ്, അതായത്, സൈൻ, കോസൈൻ എന്നിവയുടെ ഡിഗ്രികളുടെ ആകെത്തുക തുല്യവും തുല്യവുമാണ്. ഈ സമവാക്യത്തെ വിളിക്കുന്നു ഏകതാനമായആപേക്ഷികവും , കൂടാതെ നമ്പർ വിളിക്കുന്നു ഏകതാനത സൂചകം .
എങ്കിൽ, സമവാക്യം രൂപമെടുക്കുമെന്ന് വ്യക്തമാണ്:
അവയുടെ പരിഹാരങ്ങൾ മൂല്യങ്ങളാണ്, അതായത്, സംഖ്യകൾ, . ബ്രാക്കറ്റിൽ എഴുതിയ രണ്ടാമത്തെ സമവാക്യവും ഏകതാനമാണ്, എന്നാൽ ഡിഗ്രികൾ 1 കുറവാണ്.
എങ്കിൽ, ഈ സംഖ്യകൾ സമവാക്യത്തിന്റെ വേരുകളല്ല.
നമുക്ക് ലഭിക്കുമ്പോൾ: , സമവാക്യത്തിന്റെ ഇടതുവശം (1) മൂല്യം എടുക്കുന്നു.
അതിനാൽ, വേണ്ടി, ഒപ്പം, അതിനാൽ നമുക്ക് സമവാക്യത്തിന്റെ ഇരുവശങ്ങളെയും കൊണ്ട് ഹരിക്കാം. തൽഫലമായി, നമുക്ക് സമവാക്യം ലഭിക്കും:
പകരം വയ്ക്കുന്നതിലൂടെ, ബീജഗണിതത്തിലേക്ക് എളുപ്പത്തിൽ ചുരുക്കാം:
ഹോമോജീനിറ്റി ഇൻഡക്സുള്ള ഏകതാനമായ സമവാക്യങ്ങൾ 1. നമുക്ക് സമവാക്യം ഉള്ളപ്പോൾ .
എങ്കിൽ, ഈ സമവാക്യം സമവാക്യത്തിന് തുല്യമാണ്, എവിടെ നിന്ന്, .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ഈ സമവാക്യം ഒന്നാം ഡിഗ്രിയുടെ ഏകതാനമാണ്. രണ്ട് ഭാഗങ്ങളും ഹരിച്ചാൽ നമുക്ക് ലഭിക്കുന്നു: , , , .
ഉത്തരം. .
ഉദാഹരണം ഫോമിന്റെ ഒരു ഏകീകൃത സമവാക്യം നമുക്ക് ലഭിക്കുമ്പോൾ
പരിഹാരം.
എങ്കിൽ, സമവാക്യത്തിന്റെ രണ്ട് വശങ്ങളും കൊണ്ട് ഹരിച്ചാൽ, നമുക്ക് സമവാക്യം ലഭിക്കും 
, പകരം വയ്ക്കുന്നതിലൂടെ ഇത് എളുപ്പത്തിൽ ചതുരത്തിലേക്ക് ചുരുക്കാം: 
. എങ്കിൽ 
, അപ്പോൾ സമവാക്യത്തിന് യഥാർത്ഥ വേരുകളുണ്ട്, . യഥാർത്ഥ സമവാക്യത്തിന് രണ്ട് ഗ്രൂപ്പുകളുടെ പരിഹാരങ്ങൾ ഉണ്ടായിരിക്കും: , , .
എങ്കിൽ 
, അപ്പോൾ സമവാക്യത്തിന് പരിഹാരങ്ങളില്ല.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ഈ സമവാക്യം രണ്ടാം ഡിഗ്രിയുടെ ഏകതാനമാണ്. സമവാക്യത്തിന്റെ ഇരുവശങ്ങളും വിഭജിക്കുക, നമുക്ക് ലഭിക്കും: . ആകട്ടെ , എങ്കിൽ ,,. ,,; ...
ഉത്തരം.
.
സമവാക്യം രൂപത്തിന്റെ ഒരു സമവാക്യമായി ചുരുക്കിയിരിക്കുന്നു
ഇത് ചെയ്യുന്നതിന്, ഐഡന്റിറ്റി ഉപയോഗിച്ചാൽ മതി 
പ്രത്യേകിച്ചും, നമ്മൾ അതിനെ മാറ്റിസ്ഥാപിച്ചാൽ സമവാക്യം ഏകതാനമായി കുറയുന്നു 
, അപ്പോൾ നമുക്ക് തുല്യമായ ഒരു സമവാക്യം ലഭിക്കും:
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.നമുക്ക് സമവാക്യം ഒരു ഏകീകൃത രൂപത്തിലേക്ക് മാറ്റാം:
സമവാക്യത്തിന്റെ രണ്ട് വശങ്ങളും നമുക്ക് ഹരിക്കാം 
, നമുക്ക് സമവാക്യം ലഭിക്കും:
നമുക്ക് ചതുരാകൃതിയിലുള്ള സമവാക്യത്തിലേക്ക് വരാം: , 
, 
, .
ഉത്തരം.
.
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.സമവാക്യത്തിന്റെ ഇരുവശങ്ങളും ചതുരാകൃതിയിലാക്കാം പോസിറ്റീവ് മൂല്യങ്ങൾ: , ,
അത് ഇരിക്കട്ടെ, അപ്പോൾ നമുക്ക് ലഭിക്കും 
, , .
ഉത്തരം. .
ഐഡന്റിറ്റികൾ ഉപയോഗിച്ച് സമവാക്യങ്ങൾ പരിഹരിച്ചു 
ഇനിപ്പറയുന്ന സൂത്രവാക്യങ്ങൾ അറിയുന്നത് ഉപയോഗപ്രദമാണ്:
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ഉപയോഗിച്ച്, നമുക്ക് ലഭിക്കുന്നു
ഉത്തരം.
ഞങ്ങൾ ഫോർമുലകൾ സ്വയം വാഗ്ദാനം ചെയ്യുന്നില്ല, മറിച്ച് അവ നേടുന്നതിനുള്ള ഒരു രീതിയാണ്:
അതിനാൽ,
അതുപോലെ, .
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.നമുക്ക് പദപ്രയോഗം രൂപാന്തരപ്പെടുത്താം:
സമവാക്യം ഇങ്ങനെ എഴുതപ്പെടും:
സ്വീകരിക്കുന്നതിലൂടെ, നമുക്ക് ലഭിക്കുന്നു. , അതുകൊണ്ട്
ഉത്തരം. .
യൂണിവേഴ്സൽ ട്രൈഗണോമെട്രിക് സബ്സ്റ്റിറ്റ്യൂഷൻ
രൂപത്തിന്റെ ത്രികോണമിതി സമവാക്യം
എവിടെ --- യുക്തിസഹമായസൂത്രവാക്യങ്ങളുടെ സഹായത്തോടെ ഒരു ഫംഗ്ഷൻ - , അതുപോലെ സൂത്രവാക്യങ്ങളുടെ സഹായത്തോടെ - ആയി ചുരുക്കാം യുക്തിസഹമായ സമവാക്യംസാർവത്രിക ത്രികോണമിതി പകരത്തിന്റെ സൂത്രവാക്യങ്ങൾ ഉപയോഗിക്കുന്നതുമായി ബന്ധപ്പെട്ട് സമവാക്യത്തെ ഒരു ബീജഗണിത യുക്തിസഹമായ സമവാക്യത്തിലേക്ക് ചുരുക്കാൻ കഴിയുന്ന വാദങ്ങളുമായി ബന്ധപ്പെട്ട്,
സൂത്രവാക്യങ്ങളുടെ ഉപയോഗം യഥാർത്ഥ സമവാക്യത്തിന്റെ ഒഡിയുടെ സങ്കോചത്തിലേക്ക് നയിച്ചേക്കാം എന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്, കാരണം ഇത് പോയിന്റുകളിൽ നിർവചിച്ചിട്ടില്ല, അതിനാൽ അത്തരം സന്ദർഭങ്ങളിൽ കോണുകൾ യഥാർത്ഥ സമവാക്യത്തിന്റെ വേരുകളാണോ എന്ന് പരിശോധിക്കേണ്ടത് ആവശ്യമാണ്. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.ചുമതലയുടെ വ്യവസ്ഥകൾ അനുസരിച്ച്. സൂത്രവാക്യങ്ങൾ പ്രയോഗിക്കുകയും പകരം വയ്ക്കൽ നടത്തുകയും ചെയ്യുന്നു, നമുക്ക് ലഭിക്കും
എവിടെ നിന്ന് അതിനാൽ.
ഫോമിന്റെ സമവാക്യങ്ങൾ
ഫോമിന്റെ സമവാക്യങ്ങൾ , എവിടെ --- ബഹുപദം, അജ്ഞാതരുടെ പകരക്കാർ ഉപയോഗിച്ച് പരിഹരിക്കുന്നു
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.മാറ്റിസ്ഥാപിക്കുകയും അത് കണക്കിലെടുക്കുകയും ചെയ്യുന്നു, നമുക്ക് ലഭിക്കും
എവിടെ ,. --- പുറത്തുള്ളവൻറൂട്ട്, കാരണം . സമവാക്യത്തിന്റെ വേരുകൾ 
ആകുന്നു .
ഫീച്ചർ പരിമിതികൾ ഉപയോഗിക്കുന്നു
കേന്ദ്രീകൃത പരിശോധനയുടെ പ്രയോഗത്തിൽ, പരിമിതമായ പ്രവർത്തനങ്ങളെ അടിസ്ഥാനമാക്കിയുള്ള സമവാക്യങ്ങൾ നേരിടുന്നത് അത്ര വിരളമല്ല. ഉദാഹരണത്തിന്:
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.മുതൽ , , അപ്പോൾ ഇടത് വശം കവിയരുത്, എങ്കിൽ തുല്യമാണ്
രണ്ട് സമവാക്യങ്ങളും തൃപ്തിപ്പെടുത്തുന്ന മൂല്യങ്ങൾ കണ്ടെത്താൻ, ഞങ്ങൾ ഇനിപ്പറയുന്ന രീതിയിൽ തുടരുന്നു. അവയിലൊന്ന് പരിഹരിക്കാം, തുടർന്ന് കണ്ടെത്തിയ മൂല്യങ്ങളിൽ മറ്റൊന്ന് തൃപ്തിപ്പെടുത്തുന്നവ ഞങ്ങൾ തിരഞ്ഞെടുക്കും.
നമുക്ക് രണ്ടാമത്തേതിൽ നിന്ന് ആരംഭിക്കാം:, . പിന്നെ, 
.
ഇരട്ട സംഖ്യകൾക്ക് മാത്രമേ ഉണ്ടാകൂ എന്ന് വ്യക്തമാണ്.
ഉത്തരം. .
ഇനിപ്പറയുന്ന സമവാക്യം പരിഹരിച്ചുകൊണ്ട് മറ്റൊരു ആശയം സാക്ഷാത്കരിക്കപ്പെടുന്നു:
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.നമുക്ക് സ്വത്ത് ഉപയോഗിക്കാം എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്ഷൻ: , 
.
ഈ അസമത്വങ്ങളെ ടേം അനുസരിച്ച് ചേർക്കുന്നത് നമുക്ക്:
അതിനാൽ, ഈ സമവാക്യത്തിന്റെ ഇടതുവശം തുല്യമാണ്, രണ്ട് തുല്യതകൾ തൃപ്തികരമാണെങ്കിൽ മാത്രം:
അതായത്, അതിന് മൂല്യങ്ങൾ എടുക്കാം, , അല്ലെങ്കിൽ അതിന് മൂല്യങ്ങൾ എടുക്കാം, .
ഉത്തരം. , .
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം., അതിനാൽ, 
.
ഉത്തരം. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക
പരിഹാരം.നമുക്ക് സൂചിപ്പിക്കാം, അപ്പോൾ നമുക്കുള്ള വിപരീത ത്രികോണമിതി പ്രവർത്തനത്തിന്റെ നിർവചനത്തിൽ നിന്ന് 
ഒപ്പം 
.
അതിനാൽ, അസമത്വം സമവാക്യത്തിൽ നിന്ന് പിന്തുടരുന്നു, അതായത്. . പിന്നെ , പിന്നെ . എന്നിരുന്നാലും, അതുകൊണ്ടാണ്.
എങ്കിൽ, പിന്നെ. അത് മുമ്പ് സ്ഥാപിക്കപ്പെട്ടതിനാൽ, പിന്നെ.
ഉത്തരം. , .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക
പരിഹാരം.പ്രദേശം സ്വീകാര്യമായ മൂല്യങ്ങൾആണ് സമവാക്യങ്ങൾ .
ആദ്യം നമ്മൾ ഫംഗ്ഷൻ കാണിക്കുന്നു
ഏതൊരു കാര്യത്തിനും, അത് പോസിറ്റീവ് മൂല്യങ്ങൾ മാത്രമേ എടുക്കൂ.
നമുക്ക് ഫംഗ്ഷൻ ഇനിപ്പറയുന്ന രീതിയിൽ സങ്കൽപ്പിക്കാം:
മുതൽ , പിന്നീട് അത് നടക്കുന്നു, അതായത്. 
.
അതിനാൽ, അസമത്വം തെളിയിക്കാൻ, അത് കാണിക്കേണ്ടത് ആവശ്യമാണ് 
. ഈ ആവശ്യത്തിനായി, നമുക്ക് ഈ അസമത്വത്തിന്റെ ഇരുവശങ്ങളും ക്യൂബ് ചെയ്യാം
ഫലമായുണ്ടാകുന്ന സംഖ്യാ അസമത്വം അത് സൂചിപ്പിക്കുന്നു. നമ്മൾ അത് കൂടി കണക്കിലെടുക്കുകയാണെങ്കിൽ, സമവാക്യത്തിന്റെ ഇടതുവശം നോൺ-നെഗറ്റീവ് ആണ്.
ഇനി സമവാക്യത്തിന്റെ വലതുവശം നോക്കാം.
കാരണം 
, അത്
എന്നിരുന്നാലും, അത് അറിയപ്പെടുന്നു 
. അത് പിന്തുടരുന്നു, അതായത്. സമവാക്യത്തിന്റെ വലതുഭാഗം കവിയരുത്. സമവാക്യത്തിന്റെ ഇടതുവശം നെഗറ്റീവല്ലെന്ന് മുമ്പ് തെളിയിക്കപ്പെട്ടിരുന്നു, അതിനാൽ രണ്ട് വശങ്ങളും തുല്യമാണെങ്കിൽ മാത്രമേ സമത്വം സംഭവിക്കൂ, ഇത് സാധ്യമാണ്.
ഉത്തരം. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക
പരിഹാരം.നമുക്ക് സൂചിപ്പിക്കാം ഒപ്പം 
. Cauchy-Bunyakovsky അസമത്വം പ്രയോഗിച്ച്, നമുക്ക് ലഭിക്കും . അത് പിന്തുടരുന്നു 
. മറുവശത്ത്, ഉണ്ട് 
. അതിനാൽ, സമവാക്യത്തിന് വേരുകളില്ല.
ഉത്തരം. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക:
പരിഹാരം.നമുക്ക് സമവാക്യം ഇങ്ങനെ മാറ്റിയെഴുതാം:
ഉത്തരം. .
ത്രികോണമിതിയും സംയോജിത സമവാക്യങ്ങളും പരിഹരിക്കുന്നതിനുള്ള പ്രവർത്തന രീതികൾ
പരിവർത്തനങ്ങളുടെ ഫലമായി എല്ലാ സമവാക്യങ്ങളും ഒന്നോ അല്ലെങ്കിൽ മറ്റൊന്നിന്റെ സമവാക്യത്തിലേക്ക് ചുരുക്കാൻ കഴിയില്ല സാധാരണ കാഴ്ച, ഇതിനായി ഒരു പ്രത്യേക പരിഹാര രീതി ഉണ്ട്. അത്തരം സന്ദർഭങ്ങളിൽ, ഫംഗ്ഷനുകളുടെ ഗുണവിശേഷതകളും ഏകതാനത, ബൗണ്ടഡ്‌നെസ്, പാരിറ്റി, ആനുകാലികത മുതലായവ ഉപയോഗിക്കുന്നത് ഉപയോഗപ്രദമാകും. അതിനാൽ, ഫംഗ്‌ഷനുകളിലൊന്ന് കുറയുകയും രണ്ടാമത്തേത് ഇടവേളയിൽ വർദ്ധിക്കുകയും ചെയ്യുന്നുവെങ്കിൽ, സമവാക്യത്തിന് ഒരു ഈ ഇടവേളയിൽ റൂട്ട്, ഈ റൂട്ട് അദ്വിതീയമാണ്, തുടർന്ന്, ഉദാഹരണത്തിന്, തിരഞ്ഞെടുക്കുന്നതിലൂടെ ഇത് കണ്ടെത്താനാകും. ഫംഗ്ഷൻ മുകളിൽ പരിമിതപ്പെടുത്തിയിട്ടുണ്ടെങ്കിൽ, ഒപ്പം , ഫംഗ്ഷൻ താഴെയും പരിമിതപ്പെടുത്തിയിരിക്കുന്നു, കൂടാതെ, സമവാക്യം സമവാക്യങ്ങളുടെ സിസ്റ്റത്തിന് തുല്യമാണ്
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക
പരിഹാരം.യഥാർത്ഥ സമവാക്യം രൂപത്തിലേക്ക് മാറ്റാം
യുടെ ഒരു ക്വാഡ്രാറ്റിക് ആയി പരിഹരിക്കുക. അപ്പോൾ നമുക്ക് ലഭിക്കും,
ജനസംഖ്യയുടെ ആദ്യ സമവാക്യം പരിഹരിക്കാം. ഫംഗ്ഷന്റെ പരിമിതമായ സ്വഭാവം കണക്കിലെടുക്കുമ്പോൾ, സമവാക്യത്തിന് സെഗ്മെന്റിൽ മാത്രമേ റൂട്ട് ഉണ്ടാകൂ എന്ന നിഗമനത്തിൽ ഞങ്ങൾ എത്തിച്ചേരുന്നു. ഈ ഇടവേളയിൽ ഫംഗ്ഷൻ വർദ്ധിക്കുന്നു, ഒപ്പം പ്രവർത്തനവും 
കുറയുന്നു. അതിനാൽ, ഈ സമവാക്യത്തിന് ഒരു റൂട്ട് ഉണ്ടെങ്കിൽ, അത് അദ്വിതീയമാണ്. തിരഞ്ഞെടുക്കുന്നതിലൂടെ ഞങ്ങൾ കണ്ടെത്തുന്നു.
ഉത്തരം. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക
പരിഹാരം.അനുവദിക്കുക ഒപ്പം 
, അപ്പോൾ യഥാർത്ഥ സമവാക്യം ഒരു പ്രവർത്തന സമവാക്യമായി എഴുതാം. പ്രവർത്തനം വിചിത്രമായതിനാൽ, പിന്നെ . ഈ സാഹചര്യത്തിൽ, നമുക്ക് സമവാക്യം ലഭിക്കും.
ന് ഏകതാനമായതിനാൽ, സമവാക്യം സമവാക്യത്തിന് തുല്യമാണ്, അതായത്. 
, ഒരൊറ്റ റൂട്ട് ഉള്ളത്.
ഉത്തരം. .
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.ഡെറിവേറ്റീവ് സിദ്ധാന്തത്തെ അടിസ്ഥാനമാക്കി സങ്കീർണ്ണമായ പ്രവർത്തനംപ്രവർത്തനമാണെന്ന് വ്യക്തമാണ് 
കുറയുന്നു (പ്രവർത്തനം കുറയുന്നു, വർദ്ധിക്കുന്നു, കുറയുന്നു). ഇതിൽ നിന്ന് പ്രവർത്തനമാണെന്ന് വ്യക്തമാണ് 
ന് നിർവ്വചിച്ചിരിക്കുന്നു, കുറയുന്നു. അതിനാൽ, ഈ സമവാക്യത്തിന് പരമാവധി ഒരു റൂട്ട് ഉണ്ട്. കാരണം 
, അത്
ഉത്തരം. .
ഉദാഹരണം സമവാക്യം പരിഹരിക്കുക.
പരിഹാരം.നമുക്ക് മൂന്ന് ഇടവേളകളിൽ സമവാക്യം പരിഗണിക്കാം.
a) അനുവദിക്കുക. അപ്പോൾ ഈ ഗണത്തിൽ യഥാർത്ഥ സമവാക്യം സമവാക്യത്തിന് തുല്യമാണ്. ഇടവേളയിൽ ഇതിന് പരിഹാരങ്ങളൊന്നുമില്ല, കാരണം 
, എ. ഇടവേളയിൽ, യഥാർത്ഥ സമവാക്യത്തിനും വേരുകളില്ല, കാരണം 
, എ.
ബി) അനുവദിക്കുക. അപ്പോൾ ഈ ഗണത്തിൽ യഥാർത്ഥ സമവാക്യം സമവാക്യത്തിന് തുല്യമാണ്
ഇടവേളയിൽ ആരുടെ വേരുകൾ അക്കങ്ങളാണ്, ,,,.
സി) അനുവദിക്കുക. അപ്പോൾ ഈ ഗണത്തിൽ യഥാർത്ഥ സമവാക്യം സമവാക്യത്തിന് തുല്യമാണ്
ഇടവേളയിൽ ഇതിന് പരിഹാരങ്ങളൊന്നുമില്ല, കാരണം , കൂടാതെ . ഇടവേളയിൽ, സമവാക്യത്തിനും പരിഹാരങ്ങളില്ല, കാരണം , എ.
ഉത്തരം. , , , .
സമമിതി രീതി
ടാസ്‌ക്കിന്റെ രൂപീകരണത്തിന് ഒരു സമവാക്യം, അസമത്വം, സിസ്റ്റം മുതലായവയുടെ തനതായ പരിഹാരം ആവശ്യമുള്ളപ്പോൾ സമമിതി രീതി ഉപയോഗിക്കാൻ സൗകര്യപ്രദമാണ്. അല്ലെങ്കിൽ പരിഹാരങ്ങളുടെ എണ്ണത്തിന്റെ കൃത്യമായ സൂചന. ഈ സാഹചര്യത്തിൽ, നൽകിയിരിക്കുന്ന പദപ്രയോഗങ്ങളുടെ ഏതെങ്കിലും സമമിതി കണ്ടെത്തണം.
വ്യത്യസ്ത വൈവിധ്യങ്ങൾ കണക്കിലെടുക്കേണ്ടതും ആവശ്യമാണ് സാധ്യമായ തരങ്ങൾസമമിതി.
സമമിതിയോടെയുള്ള ന്യായവാദത്തിൽ യുക്തിസഹമായ ഘട്ടങ്ങൾ കർശനമായി പാലിക്കുക എന്നത് ഒരുപോലെ പ്രധാനമാണ്.
സാധാരണഗതിയിൽ, സമമിതി ഒരാളെ മാത്രം സ്ഥാപിക്കാൻ അനുവദിക്കുന്നു ആവശ്യമായ വ്യവസ്ഥകൾ, തുടർന്ന് അവയുടെ പര്യാപ്തത പരിശോധിക്കേണ്ടത് ആവശ്യമാണ്.
ഉദാഹരണം സമവാക്യത്തിന് അദ്വിതീയ പരിഹാരമുള്ള പാരാമീറ്ററിന്റെ എല്ലാ മൂല്യങ്ങളും കണ്ടെത്തുക.
പരിഹാരം.അത് ശ്രദ്ധിക്കുക ഒപ്പം --- പ്രവർത്തനങ്ങൾ പോലും, അതിനാൽ സമവാക്യത്തിന്റെ ഇടതുവശം ഒരു ഇരട്ട ഫംഗ്‌ഷനാണ്.
അങ്ങനെയാണെങ്കില് --- പരിഹാരംസമവാക്യങ്ങൾ, അതായത്, സമവാക്യത്തിന്റെ പരിഹാരവും. എങ്കിൽ --- ഒരേ ഒരു കാര്യംസമവാക്യത്തിനുള്ള പരിഹാരം, അപ്പോൾ ആവശ്യമായ , .
ഞങ്ങൾ തിരഞ്ഞെടുക്കും സാധ്യമാണ്മൂല്യങ്ങൾ, അത് സമവാക്യത്തിന്റെ റൂട്ട് ആയിരിക്കണമെന്ന് ആവശ്യപ്പെടുന്നു.
മറ്റ് മൂല്യങ്ങൾക്ക് പ്രശ്നത്തിന്റെ വ്യവസ്ഥകൾ തൃപ്തിപ്പെടുത്താൻ കഴിയില്ലെന്ന് നമുക്ക് ഉടനടി ശ്രദ്ധിക്കാം.
എന്നാൽ തിരഞ്ഞെടുത്തവരെല്ലാം യഥാർത്ഥത്തിൽ ചുമതലയുടെ വ്യവസ്ഥകൾ പാലിക്കുന്നുണ്ടോ എന്ന് ഇതുവരെ അറിവായിട്ടില്ല.
പര്യാപ്തത.
1), സമവാക്യം രൂപമെടുക്കും 
.
2), സമവാക്യം ഫോം എടുക്കും:
എല്ലാവർക്കുമായി അത് വ്യക്തമാണ് 
. അതിനാൽ, അവസാന സമവാക്യം സിസ്റ്റത്തിന് തുല്യമാണ്:
അതിനാൽ, സമവാക്യത്തിന് ഒരു അദ്വിതീയ പരിഹാരമുണ്ടെന്ന് ഞങ്ങൾ തെളിയിച്ചു.
ഉത്തരം. .
ഫംഗ്ഷൻ പര്യവേക്ഷണത്തോടുകൂടിയ പരിഹാരം
ഉദാഹരണം സമവാക്യത്തിന്റെ എല്ലാ പരിഹാരങ്ങളും തെളിയിക്കുക
മുഴുവൻ സംഖ്യകൾ.
പരിഹാരം.യഥാർത്ഥ സമവാക്യത്തിന്റെ പ്രധാന കാലഘട്ടം. അതിനാൽ, ഞങ്ങൾ ആദ്യം ഈ സമവാക്യം ഇടവേളയിൽ പരിശോധിക്കുന്നു.
നമുക്ക് സമവാക്യം ഫോമിലേക്ക് മാറ്റാം:
ഒരു മൈക്രോകാൽക്കുലേറ്റർ ഉപയോഗിച്ച് നമുക്ക് ലഭിക്കുന്നത്:
എങ്കിൽ, മുമ്പത്തെ തുല്യതകളിൽ നിന്ന് നമുക്ക് ലഭിക്കുന്നത്:
തത്ഫലമായുണ്ടാകുന്ന സമവാക്യം പരിഹരിച്ച ശേഷം, നമുക്ക് ലഭിക്കുന്നത്: .
നടത്തിയ കണക്കുകൂട്ടലുകൾ, സെഗ്മെന്റിൽ ഉൾപ്പെടുന്ന സമവാക്യത്തിന്റെ വേരുകൾ എന്ന് അനുമാനിക്കാൻ സാധ്യമാക്കുന്നു, കൂടാതെ .
നേരിട്ടുള്ള പരിശോധന ഈ സിദ്ധാന്തത്തെ സ്ഥിരീകരിക്കുന്നു. അങ്ങനെ, സമവാക്യത്തിന്റെ വേരുകൾ പൂർണ്ണസംഖ്യകൾ മാത്രമാണെന്ന് തെളിയിക്കപ്പെട്ടു.
ഉദാഹരണം
സമവാക്യം പരിഹരിക്കുക 
.
പരിഹാരം.സമവാക്യത്തിന്റെ പ്രധാന കാലയളവ് നമുക്ക് കണ്ടെത്താം. പ്രവർത്തനത്തിന് തുല്യമായ ഒരു അടിസ്ഥാന കാലയളവ് ഉണ്ട്. പ്രവർത്തനത്തിന്റെ പ്രധാന കാലഘട്ടം. ന്റെ ഏറ്റവും കുറഞ്ഞ പൊതു ഗുണിതവും തുല്യവുമാണ്. അതിനാൽ, സമവാക്യത്തിന്റെ പ്രധാന കാലഘട്ടം. അനുവദിക്കുക .
വ്യക്തമായും, ഇത് സമവാക്യത്തിനുള്ള ഒരു പരിഹാരമാണ്. ഇടവേളയിൽ. പ്രവർത്തനം നെഗറ്റീവ് ആണ്. അതിനാൽ, സമവാക്യത്തിന്റെ മറ്റ് വേരുകൾ x, എന്നീ ഇടവേളകളിൽ മാത്രമേ അന്വേഷിക്കാവൂ.
ഒരു മൈക്രോകാൽക്കുലേറ്റർ ഉപയോഗിച്ച്, സമവാക്യത്തിന്റെ വേരുകളുടെ ഏകദേശ മൂല്യങ്ങൾ ഞങ്ങൾ ആദ്യം കണ്ടെത്തുന്നു. ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ ഫംഗ്ഷൻ മൂല്യങ്ങളുടെ ഒരു പട്ടിക കംപൈൽ ചെയ്യുന്നു 
ഇടവേളകളിൽ ഒപ്പം; അതായത് ഇടവേളകളിലും.
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
പട്ടികയിൽ നിന്ന് ഇനിപ്പറയുന്ന അനുമാനങ്ങൾ എളുപ്പത്തിൽ തിരിച്ചറിയാൻ കഴിയും: സെഗ്മെന്റിൽ ഉൾപ്പെടുന്ന സമവാക്യത്തിന്റെ വേരുകൾ സംഖ്യകളാണ്: ; ; . നേരിട്ടുള്ള പരിശോധന ഈ സിദ്ധാന്തത്തെ സ്ഥിരീകരിക്കുന്നു.
ഉത്തരം.
; 
; .
യൂണിറ്റ് സർക്കിൾ ഉപയോഗിച്ച് ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നു
ത്രികോണമിതി പ്രവർത്തനങ്ങളിൽ ഒന്നായ ഫോമിന്റെ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ, അസമത്വത്തിനുള്ള പരിഹാരങ്ങൾ ഏറ്റവും വ്യക്തമായി പ്രതിനിധീകരിക്കുന്നതിനും ഉത്തരം എഴുതുന്നതിനും ഒരു ത്രികോണമിതി സർക്കിൾ ഉപയോഗിക്കുന്നത് സൗകര്യപ്രദമാണ്. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പ്രധാന മാർഗ്ഗം അവയെ തരം ലളിതമായ അസമത്വങ്ങളിലേക്ക് കുറയ്ക്കുക എന്നതാണ്. അത്തരം അസമത്വങ്ങൾ എങ്ങനെ പരിഹരിക്കാം എന്നതിന്റെ ഒരു ഉദാഹരണം നോക്കാം.
ഉദാഹരണം അസമത്വം പരിഹരിക്കുക.
പരിഹാരം.നമുക്ക് ഒരു ത്രികോണമിതി വൃത്തം വരച്ച് അതിൽ ഓർഡിനേറ്റ് കവിയുന്ന പോയിന്റുകൾ അടയാളപ്പെടുത്താം.
ഈ അസമത്വത്തിന് പരിഹാരം ആയിരിക്കും. നിശ്ചിത ഇടവേളയിൽ നിന്ന് ഏതെങ്കിലും സംഖ്യയിൽ നിന്ന് ഒരു നിശ്ചിത സംഖ്യ വ്യത്യാസപ്പെട്ടാൽ, അതും അതിൽ കുറവായിരിക്കില്ല എന്നതും വ്യക്തമാണ്. അതിനാൽ, കണ്ടെത്തിയ സൊല്യൂഷൻ സെഗ്മെന്റിന്റെ അറ്റത്ത് നിങ്ങൾ ചേർക്കേണ്ടതുണ്ട്. അവസാനമായി, യഥാർത്ഥ അസമത്വത്തിനുള്ള പരിഹാരങ്ങൾ എല്ലാം ആയിരിക്കുമെന്ന് ഞങ്ങൾ കണ്ടെത്തുന്നു 
.
ഉത്തരം.
.
ടാൻജെന്റ്, കോട്ടാൻജെന്റ് എന്നിവയുമായുള്ള അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിന്, സ്പർശനങ്ങളുടെയും കോട്ടാഞ്ചന്റുകളുടെയും ഒരു വരി എന്ന ആശയം ഉപയോഗപ്രദമാണ്. ഇവയാണ് നേർരേഖകൾ, യഥാക്രമം (ചിത്രം (1), (2) എന്നിവയിൽ), ത്രികോണമിതി വൃത്തത്തിലേക്കുള്ള ടാൻജെന്റ്.
അബ്സിസ്സ അക്ഷത്തിന്റെ പോസിറ്റീവ് ദിശയിൽ ഒരു കോണുണ്ടാക്കി, കോർഡിനേറ്റുകളുടെ ഉത്ഭവത്തിൽ അതിന്റെ ഉത്ഭവം ഉപയോഗിച്ച് ഒരു കിരണത്തെ നിർമ്മിക്കുകയാണെങ്കിൽ, ഈ കിരണത്തിന്റെ പോയിന്റ് മുതൽ വിഭജനം വരെയുള്ള ഭാഗത്തിന്റെ നീളം ഈ രശ്മി അബ്സിസ്സ അച്ചുതണ്ടിൽ ഉണ്ടാക്കുന്ന കോണിന്റെ ടാൻജെന്റിന് തുല്യമാണ് ടാൻജെന്റ് ലൈൻ. സമാനമായ നിരീക്ഷണം cotangent ന് സംഭവിക്കുന്നു.
ഉദാഹരണം അസമത്വം പരിഹരിക്കുക.
പരിഹാരം.നമുക്ക് സൂചിപ്പിക്കാം, അപ്പോൾ അസമത്വം ഏറ്റവും ലളിതമായ രൂപമെടുക്കും: . ടാൻജെന്റിന്റെ ഏറ്റവും ചെറിയ പോസിറ്റീവ് കാലയളവിന് (LPP) തുല്യമായ ദൈർഘ്യത്തിന്റെ ഒരു ഇടവേള നമുക്ക് പരിഗണിക്കാം. ഈ സെഗ്മെന്റിൽ, ടാൻജെന്റുകളുടെ ലൈൻ ഉപയോഗിച്ച്, ഞങ്ങൾ അത് സ്ഥാപിക്കുന്നു. NPP ഫംഗ്‌ഷനുകൾ മുതൽ എന്താണ് ചേർക്കേണ്ടതെന്ന് ഇപ്പോൾ നമുക്ക് ഓർക്കാം. അതിനാൽ, 
. വേരിയബിളിലേക്ക് മടങ്ങുമ്പോൾ, നമുക്ക് അത് ലഭിക്കും.
ഉത്തരം.
.
വിപരീത ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ഗ്രാഫുകൾ ഉപയോഗിച്ച് വിപരീത ത്രികോണമിതി ഫംഗ്ഷനുകളുമായുള്ള അസമത്വങ്ങൾ പരിഹരിക്കുന്നത് സൗകര്യപ്രദമാണ്. ഒരു ഉദാഹരണം ഉപയോഗിച്ച് ഇത് എങ്ങനെ ചെയ്യാമെന്ന് കാണിക്കാം.
ത്രികോണമിതി അസമത്വങ്ങൾ ഗ്രാഫിക്കായി പരിഹരിക്കുന്നു
ഒരു ആനുകാലിക ഫംഗ്ഷൻ ആണെങ്കിൽ, അസമത്വം പരിഹരിക്കുന്നതിന്, ഫംഗ്ഷന്റെ കാലയളവിന് തുല്യമായ ദൈർഘ്യമുള്ള ഒരു സെഗ്മെന്റിൽ അതിന്റെ പരിഹാരം കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. യഥാർത്ഥ അസമത്വത്തിനുള്ള എല്ലാ പരിഹാരങ്ങളും കണ്ടെത്തിയ മൂല്യങ്ങളും അതുപോലെ തന്നെ ഫംഗ്ഷന്റെ ഏതെങ്കിലും പൂർണ്ണസംഖ്യാ സംഖ്യകളാൽ കണ്ടെത്തിയതിൽ നിന്ന് വ്യത്യസ്തമായവയും ഉൾക്കൊള്ളുന്നു.
അസമത്വത്തിനുള്ള പരിഹാരം () നോക്കാം.
അതിനുശേഷം, അസമത്വത്തിന് പരിഹാരങ്ങളൊന്നുമില്ല. എങ്കിൽ, അസമത്വത്തിനുള്ള പരിഹാരങ്ങളുടെ കൂട്ടം --- ഒരു കൂട്ടംഎല്ലാ യഥാർത്ഥ സംഖ്യകളും.
അനുവദിക്കുക. സൈൻ ഫംഗ്‌ഷന് ഏറ്റവും ചെറിയ പോസിറ്റീവ് കാലയളവ് ഉണ്ട്, അതിനാൽ അസമത്വം ആദ്യം ദൈർഘ്യത്തിന്റെ ഒരു വിഭാഗത്തിൽ പരിഹരിക്കാൻ കഴിയും, ഉദാഹരണത്തിന്, സെഗ്മെന്റിൽ. ഞങ്ങൾ ഫംഗ്ഷനുകളുടെയും () ഗ്രാഫുകളും നിർമ്മിക്കുന്നു. ഫോമിലെ അസമത്വങ്ങളാൽ നൽകിയിരിക്കുന്നു: കൂടാതെ, എവിടെ നിന്ന്,
ഈ സൃഷ്ടിയിൽ, ലളിതവും ഒളിമ്പ്യാഡ് തലത്തിലുള്ളതുമായ ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുന്നതിനുള്ള രീതികൾ പരിഗണിക്കപ്പെട്ടു. ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുന്നതിനുള്ള പ്രധാന രീതികൾ പരിഗണിക്കപ്പെട്ടു, കൂടാതെ, പ്രത്യേകമായി --- സ്വഭാവംത്രികോണമിതി സമവാക്യങ്ങൾക്കും അസമത്വങ്ങൾക്കും വേണ്ടി മാത്രം, ത്രികോണമിതി സമവാക്യങ്ങളിൽ പ്രയോഗിക്കുന്നതുപോലെ സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുന്നതിനുള്ള പൊതുവായ പ്രവർത്തന രീതികൾ.
തീസിസ് അടിസ്ഥാന സൈദ്ധാന്തിക വിവരങ്ങൾ നൽകുന്നു: ത്രികോണമിതി, വിപരീത ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ നിർവചനവും ഗുണങ്ങളും; മറ്റ് ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ അടിസ്ഥാനത്തിൽ ത്രികോണമിതി ഫംഗ്‌ഷനുകൾ പ്രകടിപ്പിക്കുന്നു, ഇത് ത്രികോണമിതി പദപ്രയോഗങ്ങളെ രൂപാന്തരപ്പെടുത്തുന്നതിന് വളരെ പ്രധാനമാണ്, പ്രത്യേകിച്ച് വിപരീത ത്രികോണമിതി ഫംഗ്‌ഷനുകൾ അടങ്ങിയിരിക്കുന്നവ; സ്കൂൾ കോഴ്‌സിൽ നിന്ന് അറിയപ്പെടുന്ന അടിസ്ഥാന ത്രികോണമിതി സൂത്രവാക്യങ്ങൾക്ക് പുറമേ, വിപരീത ത്രികോണമിതി പ്രവർത്തനങ്ങൾ അടങ്ങിയ പദപ്രയോഗങ്ങൾ ലളിതമാക്കുന്ന സൂത്രവാക്യങ്ങൾ നൽകിയിരിക്കുന്നു. പ്രാഥമിക ത്രികോണമിതി സമവാക്യങ്ങളുടെ പരിഹാരം, ഫാക്‌ടറൈസേഷൻ രീതി, ത്രികോണമിതി സമവാക്യങ്ങളെ ബീജഗണിതത്തിലേക്ക് ചുരുക്കുന്നതിനുള്ള രീതികൾ എന്നിവ പരിഗണിക്കപ്പെടുന്നു. ത്രികോണമിതി സമവാക്യങ്ങൾക്കുള്ള പരിഹാരങ്ങൾ പല തരത്തിൽ എഴുതാം എന്ന വസ്തുത കാരണം, ഈ പരിഹാരങ്ങളുടെ രൂപം ഈ പരിഹാരങ്ങൾ സമാനമാണോ വ്യത്യസ്തമാണോ എന്ന് പെട്ടെന്ന് നിർണ്ണയിക്കാൻ ഒരാളെ അനുവദിക്കാത്തതിനാൽ, ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു പൊതു സ്കീം പരിഗണിക്കുകയും പരിവർത്തനം ചെയ്യുകയും ചെയ്യുന്നു. ത്രികോണമിതി സമവാക്യങ്ങളുടെ പൊതുവായ പരിഹാരങ്ങളുടെ ഗ്രൂപ്പുകളുടെ ഗ്രൂപ്പുകൾ വിശദമായി പരിഗണിക്കുന്നു. യൂണിറ്റ് സർക്കിളിലും ഗ്രാഫിക്കൽ രീതിയിലും പ്രാഥമിക ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ വിശദമായി ചർച്ചചെയ്യുന്നു. പ്രാഥമിക അസമത്വങ്ങളിലൂടെ നോൺ-എലിമെന്ററി ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്ന പ്രക്രിയയും സ്കൂൾ കുട്ടികൾക്ക് ഇതിനകം നന്നായി അറിയാവുന്ന ഇടവേളകളുടെ രീതിയും വിവരിച്ചിരിക്കുന്നു. വേരുകൾ തിരഞ്ഞെടുക്കുന്നതിനുള്ള സാധാരണ ജോലികൾക്കുള്ള പരിഹാരങ്ങൾ നൽകിയിരിക്കുന്നു. വേരുകൾ തിരഞ്ഞെടുക്കുന്നതിന് ആവശ്യമായ സൈദ്ധാന്തിക വിവരങ്ങൾ നൽകിയിരിക്കുന്നു: ഒരു കൂട്ടം പൂർണ്ണസംഖ്യകളെ വിഭജിക്കാത്ത ഉപഗണങ്ങളായി വിഭജിക്കുക, പൂർണ്ണസംഖ്യകളിലെ സമവാക്യങ്ങൾ പരിഹരിക്കുക (ഡയഫാന്റൈൻ).
ഈ തീസിസിന്റെ ഫലങ്ങൾ കോഴ്സ് വർക്ക് തയ്യാറാക്കുന്നതിലും വിദ്യാഭ്യാസപരമായ മെറ്റീരിയലായി ഉപയോഗിക്കാം പ്രബന്ധങ്ങൾ, സ്കൂൾ കുട്ടികൾക്കായി ഇലക്‌റ്റീവുകൾ കംപൈൽ ചെയ്യുമ്പോൾ, പ്രവേശന പരീക്ഷകൾക്കും കേന്ദ്രീകൃത ടെസ്റ്റിംഗിനും വിദ്യാർത്ഥികളെ തയ്യാറാക്കുന്നതിനും ഈ ജോലി ഉപയോഗിക്കാം.
വൈഗോഡ്സ്കി Ya.Ya., പ്രാഥമിക ഗണിതശാസ്ത്രത്തിന്റെ കൈപ്പുസ്തകം. /വൈഗോഡ്സ്കി യാ.യാ. --- എം.: നൗക, 1970.
ഇഗുഡിസ്മാൻ ഒ., വാക്കാലുള്ള പരീക്ഷയിലെ മാത്തമാറ്റിക്സ് / ഇഗുഡിസ്മാൻ ഒ. --- എം.: ഐറിസ് പ്രസ്സ്, റോൾഫ്, 2001.
അസറോവ് എ.ഐ., സമവാക്യങ്ങൾ/അസറോവ് എ.ഐ., ഗ്ലാഡൻ ഒ.എം., ഫെഡോസെൻകോ വി.എസ്. --- Mn.: ട്രിവിയം, 1994.
ലിറ്റ്‌വിനെങ്കോ വി.എൻ., പ്രാഥമിക ഗണിതത്തെക്കുറിച്ചുള്ള വർക്ക്‌ഷോപ്പ് / ലിറ്റ്‌വിനെങ്കോ വി.എൻ. --- എം.: വിദ്യാഭ്യാസം, 1991.
Sharygin I.F., ഗണിതത്തിലെ ഓപ്ഷണൽ കോഴ്സ്: പ്രശ്നപരിഹാരം / Sharygin I.F., Golubev V.I. --- എം.: വിദ്യാഭ്യാസം, 1991.
ബർദുഷ്കിൻ വി., ത്രികോണമിതി സമവാക്യങ്ങൾ. റൂട്ട് തിരഞ്ഞെടുക്കൽ/ബി. Bardushkin, A. Prokofiev.// മാത്തമാറ്റിക്സ്, നമ്പർ 12, 2005 പേ. 23--27.
Vasilevsky A.B., ഗണിതത്തിൽ പാഠ്യേതര ജോലികൾക്കുള്ള നിയമനങ്ങൾ / Vasilevsky A.B. --- എം.എൻ.: പീപ്പിൾസ് അശ്വേത. 1988. --- 176 പേ.
സപുനോവ് പി.ഐ., ത്രികോണമിതി സമവാക്യങ്ങളുടെ പൊതു പരിഹാരങ്ങളുടെ ഗ്രൂപ്പുകളുടെ രൂപാന്തരവും യൂണിയനും / സപുനോവ് പി.ഐ. // ഗണിതശാസ്ത്ര വിദ്യാഭ്യാസം, ലക്കം 3, 1935.
ബോറോഡിൻ പി., ത്രികോണമിതി. മെറ്റീരിയലുകൾ പ്രവേശന പരീക്ഷകൾമോസ്കോ സ്റ്റേറ്റ് യൂണിവേഴ്സിറ്റിയിൽ [ടെക്സ്റ്റ്]/പി. ബോറോഡിൻ, വി. ഗാൽക്കിൻ, വി. പാൻഫെറോവ്, ഐ. സെർജീവ്, വി. തരാസോവ് // മാത്തമാറ്റിക്സ് നമ്പർ 1, 2005 പേ. 36--48.
സാമുസെൻകോ എ.വി., ഗണിതം: സാധാരണ തെറ്റുകൾഅപേക്ഷകർ: റഫറൻസ് മാനുവൽ/സമുസെൻകോ A.V., Kazachenok V.V. --- Mn.: Higher School, 1991.
Azarov A.I., പരീക്ഷാ പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പ്രവർത്തനപരവും ഗ്രാഫിക്കൽ രീതികളും / Azarov A.I., Barvenov S.A., --- Mn.: Aversev, 2004.
ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനും ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ തിരിച്ചറിയുന്നതിനുമുള്ള ഒരു അൽഗോരിതം.
ഉന്നത വിദ്യാഭ്യാസ അധ്യാപകർ യോഗ്യതാ വിഭാഗം:
ഷിർക്കോ എഫ്.എം. പി. പുരോഗതി, MOBU-സെക്കൻഡറി സ്കൂൾ നമ്പർ 6
സങ്കിന എൽ.എസ്. അർമവീർ, പ്രൈവറ്റ് സെക്കൻഡറി സ്കൂൾ " പുതിയ വഴി»
ശാസ്ത്രവും ഗണിതവും പഠിപ്പിക്കുന്നതിന് സാർവത്രിക രീതികളൊന്നുമില്ല. ഓരോ അധ്യാപകനും തനിക്കു മാത്രം സ്വീകാര്യമായ അധ്യാപന രീതികൾ കണ്ടെത്തുന്നു.
ഞങ്ങളുടെ നിരവധി വർഷത്തെ അധ്യാപന അനുഭവം കാണിക്കുന്നത്, പഠനത്തിന്റെ പ്രാരംഭ ഘട്ടത്തിൽ അവരുടെ പ്രവർത്തനങ്ങളിൽ അൽഗോരിതം ഉപയോഗിക്കാൻ പഠിപ്പിച്ചാൽ, മെമ്മറിയിൽ വലിയ അളവിലുള്ള വിവരങ്ങൾ ഏകാഗ്രതയും നിലനിർത്തലും ആവശ്യമായ മെറ്റീരിയൽ വിദ്യാർത്ഥികൾ കൂടുതൽ എളുപ്പത്തിൽ പഠിക്കുന്നു. സങ്കീർണ്ണമായ വിഷയം. ഞങ്ങളുടെ അഭിപ്രായത്തിൽ, അത്തരമൊരു വിഷയം ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള വിഷയമാണ്.
അതിനാൽ, ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സാങ്കേതികതകളും രീതികളും തിരിച്ചറിയാൻ ഞങ്ങൾ വിദ്യാർത്ഥികളുമായി ആരംഭിക്കുന്നതിന് മുമ്പ്, ഏറ്റവും ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു അൽഗോരിതം ഞങ്ങൾ പരിശീലിക്കുകയും ഏകീകരിക്കുകയും ചെയ്യുന്നു.
ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതം
അനുബന്ധ അക്ഷത്തിൽ പോയിന്റുകൾ അടയാളപ്പെടുത്തുക ( വേണ്ടി പാപം x– OA ആക്സിസ്, വേണ്ടികോസ് x- OX അക്ഷം)
ഞങ്ങൾ അച്ചുതണ്ടിലേക്ക് ലംബമായി പുനഃസ്ഥാപിക്കുന്നു, അത് രണ്ട് പോയിന്റുകളിൽ സർക്കിളിനെ വിഭജിക്കുന്നു.
സർക്കിളിലെ ആദ്യ പോയിന്റ് നിർവചനം അനുസരിച്ച് ആർക്ക് ഫംഗ്ഷൻ ശ്രേണിയുടെ ഇടവേളയിൽ ഉൾപ്പെടുന്ന ഒരു പോയിന്റാണ്.
ലേബൽ ചെയ്ത പോയിന്റിൽ നിന്ന് ആരംഭിച്ച്, അച്ചുതണ്ടിന്റെ ഷേഡുള്ള ഭാഗത്തിന് അനുയോജ്യമായ വൃത്തത്തിന്റെ ആർക്ക് ഷേഡ് ചെയ്യുക.
ദയവായി ശ്രദ്ധിക്കുക പ്രത്യേക ശ്രദ്ധവഴിമാറിയ ദിശയിലേക്ക്. ട്രാവെർസൽ ഘടികാരദിശയിലാണെങ്കിൽ (അതായത് 0 വഴി ഒരു പരിവർത്തനം ഉണ്ട്), അപ്പോൾ വൃത്തത്തിലെ രണ്ടാമത്തെ പോയിന്റ് നെഗറ്റീവ് ആയിരിക്കും, എതിർ ഘടികാരദിശയിലാണെങ്കിൽ അത് പോസിറ്റീവ് ആയിരിക്കും.
ഫംഗ്ഷന്റെ ആനുകാലികത കണക്കിലെടുത്ത് ഞങ്ങൾ ഒരു ഇടവേളയുടെ രൂപത്തിൽ ഉത്തരം എഴുതുന്നു.
ഉദാഹരണങ്ങൾ ഉപയോഗിച്ച് അൽഗോരിതത്തിന്റെ പ്രവർത്തനം നോക്കാം.
1) പാപം ≥ 1/2;
പരിഹാരം:
ഞങ്ങൾ ഒരു യൂണിറ്റ് സർക്കിൾ ചിത്രീകരിക്കുന്നു.;
OU അക്ഷത്തിൽ ഞങ്ങൾ പോയിന്റ് ½ അടയാളപ്പെടുത്തുന്നു.
ഞങ്ങൾ അക്ഷത്തിന് ലംബമായി പുനഃസ്ഥാപിക്കുന്നു,
ഇത് വൃത്തത്തെ രണ്ട് പോയിന്റുകളിൽ വിഭജിക്കുന്നു.
ആർക്സൈനിന്റെ നിർവചനം അനുസരിച്ച്, ഞങ്ങൾ ആദ്യം ശ്രദ്ധിക്കുന്നു
പോയിന്റ് π/6.
അച്ചുതണ്ടിനോട് യോജിക്കുന്ന ഭാഗം ഷേഡ് ചെയ്യുക
നൽകിയ അസമത്വം, പോയിന്റ് ½ ന് മുകളിൽ.
അച്ചുതണ്ടിന്റെ ഷേഡുള്ള ഭാഗത്തിന് അനുയോജ്യമായ വൃത്തത്തിന്റെ ആർക്ക് ഷേഡ് ചെയ്യുക.
ട്രാവർസൽ എതിർ ഘടികാരദിശയിലാണ് ചെയ്യുന്നത്, നമുക്ക് പോയിന്റ് 5π/6 ലഭിക്കും.
ഫംഗ്ഷന്റെ ആനുകാലികത കണക്കിലെടുത്ത് ഞങ്ങൾ ഒരു ഇടവേളയുടെ രൂപത്തിൽ ഉത്തരം എഴുതുന്നു;
ഉത്തരം:x;[π/6 + 2π എൻ, 5π/6 + 2π എൻ], എൻ Z.
ഉത്തര രേഖയിൽ ഒരു പട്ടിക മൂല്യം ഇല്ലെങ്കിൽ, അതേ അൽഗോരിതം ഉപയോഗിച്ച് ഏറ്റവും ലളിതമായ അസമത്വം പരിഹരിക്കപ്പെടും.
വിദ്യാർത്ഥികൾ, അവരുടെ ആദ്യ പാഠങ്ങളിൽ ബോർഡിലെ അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ, അൽഗോരിതത്തിന്റെ ഓരോ ഘട്ടവും ഉറക്കെ ചൊല്ലുക.
2) 5 കോസ് x – 1 ≥ 0;
ആർ 
പരിഹാരം:ചെയ്തത്
5 കോസ് x – 1 ≥ 0;
കോസ് x ≥ 1/5;
ഒരു യൂണിറ്റ് സർക്കിൾ വരയ്ക്കുക.
OX അക്ഷത്തിൽ 1/5 കോർഡിനേറ്റ് ഉപയോഗിച്ച് ഞങ്ങൾ ഒരു പോയിന്റ് അടയാളപ്പെടുത്തുന്നു.
ഞങ്ങൾ അച്ചുതണ്ടിലേക്ക് ലംബമായി പുനഃസ്ഥാപിക്കുന്നു, ഏത്
രണ്ട് പോയിന്റുകളിൽ വൃത്തത്തെ വിഭജിക്കുന്നു.
വൃത്തത്തിലെ ആദ്യ പോയിന്റ് നിർവചനം അനുസരിച്ച് ആർക്ക് കോസൈൻ ശ്രേണിയുടെ ഇടവേളയിൽ ഉൾപ്പെടുന്ന ഒരു പോയിന്റാണ് (0; π).
ഈ അസമത്വവുമായി പൊരുത്തപ്പെടുന്ന അച്ചുതണ്ടിന്റെ ഭാഗം ഞങ്ങൾ നിഴൽ ചെയ്യുന്നു.
ഒപ്പിട്ട പോയിന്റിൽ നിന്ന് ആരംഭിക്കുന്നു ആർക്കോസ് 1/5, അച്ചുതണ്ടിന്റെ ഷേഡുള്ള ഭാഗത്തിന് അനുയോജ്യമായ വൃത്തത്തിന്റെ ആർക്ക് ഷേഡ് ചെയ്യുക.
ട്രാവെർസൽ ഘടികാരദിശയിലാണ് ചെയ്യുന്നത് (അതായത് 0 വഴി ഒരു പരിവർത്തനം ഉണ്ട്), അതായത് സർക്കിളിലെ രണ്ടാമത്തെ പോയിന്റ് നെഗറ്റീവ് ആയിരിക്കും - ആർക്കോസ് 1/5.
ചെറിയ മൂല്യം മുതൽ വലുത് വരെയുള്ള ഫംഗ്ഷന്റെ ആനുകാലികത കണക്കിലെടുത്ത് ഞങ്ങൾ ഒരു ഇടവേളയുടെ രൂപത്തിൽ ഉത്തരം എഴുതുന്നു.
ഉത്തരം: x [-ആർക്കോസ് 1/5 + 2π എൻ, ആർക്കോസ് 1/5 + 2π എൻ], എൻ Z.
ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കാനുള്ള കഴിവ് മെച്ചപ്പെടുത്തുന്നത് ഇനിപ്പറയുന്ന ചോദ്യങ്ങളാൽ സുഗമമാക്കുന്നു: "ഒരു കൂട്ടം അസമത്വങ്ങൾ ഞങ്ങൾ എങ്ങനെ പരിഹരിക്കും?"; "ഒരു അസമത്വം മറ്റൊന്നിൽ നിന്ന് എങ്ങനെ വ്യത്യാസപ്പെട്ടിരിക്കുന്നു?"; "ഒരു അസമത്വം മറ്റൊന്നുമായി എങ്ങനെ സാമ്യമുള്ളതാണ്?"; കർശനമായ അസമത്വം നൽകിയാൽ ഉത്തരം എങ്ങനെ മാറും?"; "" എന്ന ചിഹ്നത്തിന് പകരം ഒരു അടയാളം ഉണ്ടെങ്കിൽ ഉത്തരം എങ്ങനെ മാറും
അവ പരിഹരിക്കുന്നതിനുള്ള രീതികളുടെ കാഴ്ചപ്പാടിൽ നിന്ന് അസമത്വങ്ങളുടെ ഒരു ലിസ്റ്റ് വിശകലനം ചെയ്യുന്നതിനുള്ള ചുമതല അവരുടെ തിരിച്ചറിയൽ പരിശീലിക്കാൻ നിങ്ങളെ അനുവദിക്കുന്നു.
ക്ലാസിൽ പരിഹരിക്കേണ്ട അസമത്വങ്ങൾ വിദ്യാർത്ഥികൾക്ക് നൽകുന്നു.
ചോദ്യം:ഒരു ത്രികോണമിതി അസമത്വം അതിന്റെ ഏറ്റവും ലളിതമായ രൂപത്തിലേക്ക് കുറയ്ക്കുമ്പോൾ തുല്യമായ പരിവർത്തനങ്ങൾ ആവശ്യമായ അസമത്വങ്ങൾ ഹൈലൈറ്റ് ചെയ്യണോ?
ഉത്തരം 1, 3, 5.
ചോദ്യം:സങ്കീർണ്ണമായ ഒരു വാദത്തെ ലളിതമായ ഒന്നായി നിങ്ങൾ പരിഗണിക്കേണ്ട അസമത്വങ്ങൾ എന്തൊക്കെയാണ്?
ഉത്തരം: 1, 2, 3, 5, 6.
ചോദ്യം:അവ പ്രയോഗിക്കാൻ കഴിയുന്ന അസമത്വങ്ങൾക്ക് പേര് നൽകുക ത്രികോണമിതി സൂത്രവാക്യങ്ങൾ?
ഉത്തരം: 2, 3, 6.
ചോദ്യം:ഒരു പുതിയ വേരിയബിൾ അവതരിപ്പിക്കുന്ന രീതി പ്രയോഗിക്കാൻ കഴിയുന്ന അസമത്വങ്ങൾക്ക് പേര് നൽകുക?
ഉത്തരം: 6.
അവ പരിഹരിക്കുന്നതിനുള്ള രീതികളുടെ കാഴ്ചപ്പാടിൽ നിന്ന് അസമത്വങ്ങളുടെ ഒരു ലിസ്റ്റ് വിശകലനം ചെയ്യുന്നതിനുള്ള ചുമതല അവരുടെ തിരിച്ചറിയൽ പരിശീലിക്കാൻ നിങ്ങളെ അനുവദിക്കുന്നു. കഴിവുകൾ വികസിപ്പിക്കുമ്പോൾ, അത് നടപ്പിലാക്കുന്നതിന്റെ ഘട്ടങ്ങൾ തിരിച്ചറിയുകയും അവ രൂപപ്പെടുത്തുകയും ചെയ്യേണ്ടത് പ്രധാനമാണ് പൊതുവായ കാഴ്ച, ഏറ്റവും ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതത്തിൽ അവതരിപ്പിച്ചിരിക്കുന്നു.
ആൾജിബ്ര പ്രോജക്റ്റ് "ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നു" പത്താം ക്ലാസ് വിദ്യാർത്ഥി "ബി" കസാച്ച്കോവ യൂലിയ സൂപ്പർവൈസർ പൂർത്തിയാക്കി: ഗണിതശാസ്ത്ര അദ്ധ്യാപകൻ കൊചകോവ എൻ.എൻ.
ലക്ഷ്യം "ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നു" എന്ന വിഷയത്തെക്കുറിച്ചുള്ള മെറ്റീരിയൽ ഏകീകരിക്കുകയും വരാനിരിക്കുന്ന പരീക്ഷയ്ക്ക് തയ്യാറെടുക്കാൻ വിദ്യാർത്ഥികൾക്ക് ഒരു ഓർമ്മപ്പെടുത്തൽ സൃഷ്ടിക്കുകയും ചെയ്യുക.
ലക്ഷ്യങ്ങൾ: ഈ വിഷയത്തെക്കുറിച്ചുള്ള മെറ്റീരിയൽ സംഗ്രഹിക്കുക. ലഭിച്ച വിവരങ്ങൾ വ്യവസ്ഥാപിതമാക്കുക. ഏകീകൃത സംസ്ഥാന പരീക്ഷയിൽ ഈ വിഷയം പരിഗണിക്കുക.
"ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുക" എന്ന വിഷയത്തിലെ ചുമതലകൾ ഏകീകൃത സംസ്ഥാന പരീക്ഷയുടെ ചുമതലകളിൽ ഉൾപ്പെടുത്തിയിട്ടുണ്ട് എന്ന വസ്തുതയിലാണ് ഞാൻ തിരഞ്ഞെടുത്ത വിഷയത്തിന്റെ പ്രസക്തി.
ത്രികോണമിതി അസമത്വങ്ങൾ രണ്ട് സംഖ്യകളെയോ പദപ്രയോഗങ്ങളെയോ ഒരു ചിഹ്നത്തിലൂടെ ബന്ധിപ്പിക്കുന്ന ഒരു ബന്ധമാണ് അസമത്വം: (അതിനേക്കാൾ വലുത്); ≥ (അതിനേക്കാൾ വലുതോ തുല്യമോ). ഒരു ത്രികോണമിതി അസമത്വം ത്രികോണമിതി പ്രവർത്തനങ്ങൾ ഉൾപ്പെടുന്ന ഒരു അസമത്വമാണ്.
ത്രികോണമിതി അസമത്വങ്ങൾ ത്രികോണമിതി ഫംഗ്‌ഷനുകൾ അടങ്ങിയ അസമത്വങ്ങളുടെ പരിഹാരം, ചട്ടം പോലെ, രൂപത്തിന്റെ ഏറ്റവും ലളിതമായ അസമത്വങ്ങളുടെ പരിഹാരമായി ചുരുക്കിയിരിക്കുന്നു: sin x>a, sin x a, cos x a, tg x a,ctg x
ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതം നൽകിയിരിക്കുന്ന ത്രികോണമിതി ഫംഗ്ഷനുമായി ബന്ധപ്പെട്ട അക്ഷത്തിൽ, ഇത് അടയാളപ്പെടുത്തുക സംഖ്യാ മൂല്യംഈ പ്രവർത്തനം. യൂണിറ്റ് സർക്കിളിനെ വിഭജിക്കുന്ന അടയാളപ്പെടുത്തിയ പോയിന്റിലൂടെ ഒരു രേഖ വരയ്ക്കുക. കർശനമായതോ അല്ലാത്തതോ ആയ അസമത്വ ചിഹ്നം കണക്കിലെടുത്ത് ഒരു വരിയുടെയും ഒരു വൃത്തത്തിന്റെയും കവല പോയിന്റുകൾ തിരഞ്ഞെടുക്കുക. അസമത്വത്തിനുള്ള പരിഹാരങ്ങൾ സ്ഥിതിചെയ്യുന്ന സർക്കിളിന്റെ ആർക്ക് തിരഞ്ഞെടുക്കുക. വൃത്താകൃതിയിലുള്ള ആർക്കിന്റെ ആരംഭ, അവസാന പോയിന്റുകളിൽ ആംഗിൾ മൂല്യങ്ങൾ നിർണ്ണയിക്കുക. നൽകിയിരിക്കുന്ന ത്രികോണമിതി പ്രവർത്തനത്തിന്റെ ആനുകാലികത കണക്കിലെടുത്ത് അസമത്വത്തിനുള്ള പരിഹാരം എഴുതുക.
ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സൂത്രവാക്യങ്ങൾ sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx എ; x (- arccos a + 2πn; arccos a + 2πn). cosxഎ; x (arctg a + πn ; + πn). tgx എ; x (πn ; arctan + πn). ctgx
ഗ്രാഫിക് പരിഹാരംഅടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങൾ sinx >a
അടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങളുടെ ഗ്രാഫിക്കൽ പരിഹാരം sinx അടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങളുടെ ഗ്രാഫിക്കൽ പരിഹാരം cosx >a അടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങളുടെ ഗ്രാഫിക്കൽ പരിഹാരം cosx അടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങളുടെ ഗ്രാഫിക്കൽ പരിഹാരം tgx >a അടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങളുടെ ഗ്രാഫിക്കൽ പരിഹാരം tgx അടിസ്ഥാന ത്രികോണമിതി അസമത്വങ്ങളുടെ ഗ്രാഫിക് പരിഹാരം ctgx >a
ത്രികോണമിതി ഫംഗ്‌ഷനുകൾ അടങ്ങിയ അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ, അവ cos(t)>a, sint(t)=a എന്നീ രൂപങ്ങളുടെ ഏറ്റവും ലളിതമായ അസമത്വങ്ങളിലേക്കും സമാനമായവയിലേക്കും ചുരുങ്ങുന്നു. ഇതിനകം തന്നെ ഏറ്റവും ലളിതമായ അസമത്വങ്ങൾ പരിഹരിച്ചു. നമുക്ക് നോക്കാം വിവിധ ഉദാഹരണങ്ങൾലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കാനുള്ള വഴികൾ.
ഉദാഹരണം 1. അസമത്വം പരിഹരിക്കുക sin(t) > = -1/2.
ഒരു യൂണിറ്റ് സർക്കിൾ വരയ്ക്കുക. നിർവചനം അനുസരിച്ച് sin(t) y കോർഡിനേറ്റ് ആയതിനാൽ, Oy അക്ഷത്തിൽ y = -1/2 എന്ന പോയിന്റ് ഞങ്ങൾ അടയാളപ്പെടുത്തുന്നു. ഓക്സ് അക്ഷത്തിന് സമാന്തരമായി ഞങ്ങൾ അതിലൂടെ ഒരു നേർരേഖ വരയ്ക്കുന്നു. യൂണിറ്റ് സർക്കിളിന്റെ ഗ്രാഫ് ഉപയോഗിച്ച് നേർരേഖയുടെ കവലയിൽ, പോയിന്റുകൾ Pt1, Pt2 എന്നിവ അടയാളപ്പെടുത്തുക. Pt1, Pt2 എന്നീ പോയിന്റുകളുമായി ഞങ്ങൾ കോർഡിനേറ്റുകളുടെ ഉത്ഭവത്തെ രണ്ട് സെഗ്മെന്റുകളായി ബന്ധിപ്പിക്കുന്നു.
ഈ അസമത്വത്തിനുള്ള പരിഹാരം ഈ പോയിന്റുകൾക്ക് മുകളിൽ സ്ഥിതി ചെയ്യുന്ന യൂണിറ്റ് സർക്കിളിന്റെ എല്ലാ പോയിന്റുകളും ആയിരിക്കും. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, പരിഹാരം ആർക്ക് എൽ ആയിരിക്കും. ഇപ്പോൾ ആർക്ക് എൽ-ന് അനിയന്ത്രിതമായ പോയിന്റ് ഉൾപ്പെടുന്ന വ്യവസ്ഥകൾ സൂചിപ്പിക്കേണ്ടത് ആവശ്യമാണ്.
Pt1 വലത് അർദ്ധവൃത്തത്തിലാണ്, അതിന്റെ ഓർഡിനേറ്റ് -1/2 ആണ്, തുടർന്ന് t1=arcsin(-1/2) = - pi/6. പോയിന്റ് Pt1 വിവരിക്കാൻ, നിങ്ങൾക്ക് ഇനിപ്പറയുന്ന ഫോർമുല എഴുതാം:
t2 = pi - arcsin(-1/2) = 7*pi/6. തൽഫലമായി, t-യ്‌ക്ക് ഇനിപ്പറയുന്ന അസമത്വം ഞങ്ങൾ നേടുന്നു:
ഞങ്ങൾ അസമത്വങ്ങൾ സംരക്ഷിക്കുന്നു. സൈൻ ഫംഗ്ഷൻ ആനുകാലികമായതിനാൽ, ഓരോ 2*പൈയിലും പരിഹാരങ്ങൾ ആവർത്തിക്കും എന്നാണ് ഇതിനർത്ഥം. t യുടെ ഫലമായുണ്ടാകുന്ന അസമത്വത്തിലേക്ക് ഞങ്ങൾ ഈ അവസ്ഥ ചേർക്കുകയും ഉത്തരം എഴുതുകയും ചെയ്യുന്നു.
ഉത്തരം: -pi/6+2*pi*n< = t < = 7*pi/6 + 2*pi*n, при любом целом n.
ഉദാഹരണം 2.കോസ്(ടി) അസമത്വം പരിഹരിക്കുക<1/2.
നമുക്ക് ഒരു യൂണിറ്റ് സർക്കിൾ വരയ്ക്കാം. നിർവചനം അനുസരിച്ച്, cos(t) എന്നത് x കോർഡിനേറ്റ് ആയതിനാൽ, Ox അക്ഷത്തിലെ ഗ്രാഫിൽ നമ്മൾ പോയിന്റ് x = 1/2 അടയാളപ്പെടുത്തുന്നു.
Oy അക്ഷത്തിന് സമാന്തരമായി ഈ പോയിന്റിലൂടെ ഞങ്ങൾ ഒരു നേർരേഖ വരയ്ക്കുന്നു. യൂണിറ്റ് സർക്കിളിന്റെ ഗ്രാഫ് ഉപയോഗിച്ച് നേർരേഖയുടെ കവലയിൽ, പോയിന്റുകൾ Pt1, Pt2 എന്നിവ അടയാളപ്പെടുത്തുക. Pt1, Pt2 എന്നീ പോയിന്റുകളുമായി ഞങ്ങൾ കോർഡിനേറ്റുകളുടെ ഉത്ഭവത്തെ രണ്ട് സെഗ്മെന്റുകളായി ബന്ധിപ്പിക്കുന്നു.
ആർക്ക് l യുടെ യൂണിറ്റ് സർക്കിളിന്റെ എല്ലാ പോയിന്റുകളും ആയിരിക്കും പരിഹാരങ്ങൾ. നമുക്ക് t1, t2 എന്നീ പോയിന്റുകൾ കണ്ടെത്താം.
t1 = ആർക്കോസ്(1/2) = പൈ/3.
t2 = 2*pi - arccos(1/2) = 2*pi-pi/3 = 5*pi/6.
t: pi/3 എന്നതിനായുള്ള അസമത്വം ഞങ്ങൾക്ക് ലഭിച്ചു കോസൈൻ ഒരു ആനുകാലിക പ്രവർത്തനമായതിനാൽ, ഓരോ 2*പൈയിലും പരിഹാരങ്ങൾ ആവർത്തിക്കും. t യുടെ ഫലമായുണ്ടാകുന്ന അസമത്വത്തിലേക്ക് ഞങ്ങൾ ഈ അവസ്ഥ ചേർക്കുകയും ഉത്തരം എഴുതുകയും ചെയ്യുന്നു. ഉത്തരം: pi/3+2*pi*n ഉദാഹരണം 3.അസമത്വം പരിഹരിക്കുക tg(t)< = 1. ടാൻജെന്റ് പിരീഡ് പൈയ്ക്ക് തുല്യമാണ്. വലത് അർദ്ധവൃത്തത്തിന്റെ ഇടവേളയിൽ (-pi/2;pi/2) ഉൾപ്പെടുന്ന പരിഹാരങ്ങൾ നമുക്ക് കണ്ടെത്താം. അടുത്തതായി, സ്പർശനത്തിന്റെ ആനുകാലികത ഉപയോഗിച്ച്, ഈ അസമത്വത്തിനുള്ള എല്ലാ പരിഹാരങ്ങളും ഞങ്ങൾ എഴുതുന്നു. നമുക്ക് ഒരു യൂണിറ്റ് സർക്കിൾ വരച്ച് അതിൽ സ്പർശനങ്ങളുടെ ഒരു രേഖ അടയാളപ്പെടുത്താം. t അസമത്വത്തിന് ഒരു പരിഹാരമാണെങ്കിൽ, T = tg(t) എന്ന ബിന്ദുവിന്റെ ഓർഡിനേറ്റ് 1-നേക്കാൾ കുറവോ തുല്യമോ ആയിരിക്കണം. ഈ കിരണത്തിന്റെ പോയിന്റുകളുമായി പൊരുത്തപ്പെടുന്ന Pt പോയിന്റുകളുടെ കൂട്ടം ആർക്ക് l ആണ്. മാത്രമല്ല, പോയിന്റ് P(-pi/2) ഈ ആർക്കിൽ ഉൾപ്പെടുന്നില്ല. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ
പ്രസക്തി.
ചരിത്രപരമായി, ത്രികോണമിതി സമവാക്യങ്ങൾക്കും അസമത്വങ്ങൾക്കും സ്കൂൾ പാഠ്യപദ്ധതിയിൽ പ്രത്യേക സ്ഥാനം നൽകിയിട്ടുണ്ട്. സ്കൂൾ കോഴ്സിലെ ഏറ്റവും പ്രധാനപ്പെട്ട വിഭാഗങ്ങളിലൊന്നാണ് ത്രികോണമിതി എന്നും പൊതുവെ മുഴുവൻ ഗണിത ശാസ്ത്രവും ആണെന്ന് നമുക്ക് പറയാം. ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും സെക്കൻഡറി സ്കൂൾ മാത്തമാറ്റിക്സ് കോഴ്സിലെ കേന്ദ്ര സ്ഥാനങ്ങളിലൊന്നാണ്, വിദ്യാഭ്യാസ സാമഗ്രികളുടെ ഉള്ളടക്കം, വിദ്യാഭ്യാസ, വൈജ്ഞാനിക പ്രവർത്തന രീതികൾ എന്നിവ അവരുടെ പഠനസമയത്ത് രൂപപ്പെടുത്തുകയും അവ പരിഹരിക്കാൻ പ്രയോഗിക്കുകയും വേണം. സൈദ്ധാന്തികവും പ്രായോഗികവുമായ സ്വഭാവമുള്ള പ്രശ്നങ്ങൾ. ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുന്നത് ത്രികോണമിതിയിലെ എല്ലാ വിദ്യാഭ്യാസ സാമഗ്രികളുമായും ബന്ധപ്പെട്ട വിദ്യാർത്ഥികളുടെ അറിവ് ചിട്ടപ്പെടുത്തുന്നതിനുള്ള മുൻവ്യവസ്ഥകൾ സൃഷ്ടിക്കുന്നു (ഉദാഹരണത്തിന്, ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ ഗുണവിശേഷതകൾ, ത്രികോണമിതി പദപ്രയോഗങ്ങൾ രൂപാന്തരപ്പെടുത്തുന്ന രീതികൾ മുതലായവ) കൂടാതെ പഠിച്ച മെറ്റീരിയലുമായി ഫലപ്രദമായ ബന്ധം സ്ഥാപിക്കുന്നത് സാധ്യമാക്കുന്നു. ബീജഗണിതത്തിൽ (സമവാക്യങ്ങൾ, സമവാക്യങ്ങളുടെ തുല്യത, അസമത്വങ്ങൾ, ബീജഗണിത പദപ്രയോഗങ്ങളുടെ സമാന രൂപാന്തരങ്ങൾ മുതലായവ). മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ത്രികോണമിതി സമവാക്യങ്ങളും അസമത്വങ്ങളും പരിഹരിക്കുന്നതിനുള്ള സാങ്കേതിക വിദ്യകൾ പരിഗണിക്കുന്നത് ഈ കഴിവുകളെ പുതിയ ഉള്ളടക്കത്തിലേക്ക് മാറ്റുന്നത് ഉൾപ്പെടുന്നു. സിദ്ധാന്തത്തിന്റെ പ്രാധാന്യവും അതിന്റെ നിരവധി പ്രയോഗങ്ങളും തിരഞ്ഞെടുത്ത വിഷയത്തിന്റെ പ്രസക്തിയുടെ തെളിവാണ്. കോഴ്സ് ജോലിയുടെ ലക്ഷ്യങ്ങളും ലക്ഷ്യങ്ങളും ഗവേഷണ വിഷയവും നിർണ്ണയിക്കാൻ ഇത് നിങ്ങളെ അനുവദിക്കുന്നു. പഠനത്തിന്റെ ഉദ്ദേശം:
ലഭ്യമായ തരത്തിലുള്ള ത്രികോണമിതി അസമത്വങ്ങൾ, അവ പരിഹരിക്കുന്നതിനുള്ള അടിസ്ഥാനവും പ്രത്യേകവുമായ രീതികൾ സാമാന്യവൽക്കരിക്കുക, സ്കൂൾ കുട്ടികൾ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു കൂട്ടം പ്രശ്നങ്ങൾ തിരഞ്ഞെടുക്കുക. ഗവേഷണ ലക്ഷ്യങ്ങൾ:
1. ഗവേഷണ വിഷയത്തിൽ ലഭ്യമായ സാഹിത്യത്തിന്റെ വിശകലനത്തെ അടിസ്ഥാനമാക്കി, മെറ്റീരിയൽ ചിട്ടപ്പെടുത്തുക. 2. "ത്രികോണമിതി അസമത്വങ്ങൾ" എന്ന വിഷയം ഏകീകരിക്കുന്നതിന് ആവശ്യമായ ഒരു കൂട്ടം ജോലികൾ നൽകുക. പഠന വിഷയം
സ്കൂൾ മാത്തമാറ്റിക്സ് കോഴ്സിലെ ത്രികോണമിതി അസമത്വങ്ങളാണ്. പഠന വിഷയം:
ത്രികോണമിതി അസമത്വങ്ങളുടെ തരങ്ങളും അവ പരിഹരിക്കുന്നതിനുള്ള രീതികളും. സൈദ്ധാന്തിക പ്രാധാന്യം
മെറ്റീരിയൽ വ്യവസ്ഥാപിതമാക്കുക എന്നതാണ്. പ്രായോഗിക പ്രാധാന്യം:
പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിൽ സൈദ്ധാന്തിക അറിവിന്റെ പ്രയോഗം; ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പ്രധാന പൊതു രീതികളുടെ വിശകലനം. ഗവേഷണ രീതികൾ
: ശാസ്ത്രീയ സാഹിത്യത്തിന്റെ വിശകലനം, നേടിയ അറിവിന്റെ സമന്വയവും പൊതുവൽക്കരണവും, പ്രശ്നപരിഹാരത്തിന്റെ വിശകലനം, അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒപ്റ്റിമൽ രീതികൾക്കായി തിരയുക. §1.
ത്രികോണമിതി അസമത്വങ്ങളുടെ തരങ്ങളും അവ പരിഹരിക്കുന്നതിനുള്ള അടിസ്ഥാന രീതികളും
1.1 ഏറ്റവും ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ
ചിഹ്നം അല്ലെങ്കിൽ > ഉപയോഗിച്ച് ബന്ധിപ്പിച്ചിരിക്കുന്ന രണ്ട് ത്രികോണമിതി പദപ്രയോഗങ്ങളെ ത്രികോണമിതി അസമത്വങ്ങൾ എന്ന് വിളിക്കുന്നു. ഒരു ത്രികോണമിതി അസമത്വം പരിഹരിക്കുക എന്നതിനർത്ഥം അസമത്വം തൃപ്തിപ്പെടുത്തുന്ന അസമത്വത്തിൽ ഉൾപ്പെട്ടിരിക്കുന്ന അജ്ഞാതരുടെ മൂല്യങ്ങളുടെ കൂട്ടം കണ്ടെത്തുക എന്നാണ്. ത്രികോണമിതി അസമത്വങ്ങളുടെ പ്രധാന ഭാഗം അവയെ ലളിതമായ പരിഹാരത്തിലേക്ക് ചുരുക്കിക്കൊണ്ട് പരിഹരിക്കുന്നു: ഇത് ഫാക്‌ടറൈസേഷന്റെ ഒരു രീതിയായിരിക്കാം, വേരിയബിളിന്റെ മാറ്റം ( ഏറ്റവും ലളിതമായ അസമത്വങ്ങൾ രണ്ട് തരത്തിൽ പരിഹരിക്കാൻ കഴിയും: യൂണിറ്റ് സർക്കിൾ അല്ലെങ്കിൽ ഗ്രാഫിക്കായി. അനുവദിക്കുകf(x
- അടിസ്ഥാന ത്രികോണമിതി പ്രവർത്തനങ്ങളിൽ ഒന്ന്. അസമത്വം പരിഹരിക്കാൻ അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു അൽഗോരിതത്തിന്റെ ഒരു ഉദാഹരണം നമുക്ക് നൽകാം അസമത്വം പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതം 1. ഒരു സംഖ്യയുടെ സൈനിന്റെ നിർവചനം രൂപപ്പെടുത്തുകx
യൂണിറ്റ് സർക്കിളിൽ. 3. ഓർഡിനേറ്റ് അക്ഷത്തിൽ, കോർഡിനേറ്റ് ഉപയോഗിച്ച് പോയിന്റ് അടയാളപ്പെടുത്തുകഎ
.
4. ഈ ബിന്ദുവിലൂടെ OX അച്ചുതണ്ടിന് സമാന്തരമായി ഒരു രേഖ വരച്ച് അതിന്റെ കവല പോയിന്റുകൾ സർക്കിളിൽ അടയാളപ്പെടുത്തുക. 5. ഒരു സർക്കിളിന്റെ ഒരു ആർക്ക് തിരഞ്ഞെടുക്കുക, അതിൽ എല്ലാ പോയിന്റുകൾക്കും ഓർഡിനേറ്റ് കുറവാണ്എ
.
6. റൗണ്ടിന്റെ ദിശ സൂചിപ്പിക്കുക (എതിർ ഘടികാരദിശയിൽ) കൂടാതെ ഫംഗ്ഷന്റെ കാലയളവ് ഇടവേളയുടെ അറ്റത്ത് ചേർത്ത് ഉത്തരം എഴുതുക2πn
,
അസമത്വം പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതം 1. ഒരു സംഖ്യയുടെ സ്പർശനത്തിന്റെ നിർവചനം രൂപപ്പെടുത്തുകx
യൂണിറ്റ് സർക്കിളിൽ. 2. ഒരു യൂണിറ്റ് സർക്കിൾ വരയ്ക്കുക. 3. ടാൻജെന്റുകളുടെ ഒരു രേഖ വരച്ച് അതിൽ ഒരു ഓർഡിനേറ്റ് ഉപയോഗിച്ച് ഒരു പോയിന്റ് അടയാളപ്പെടുത്തുകഎ
.
4. ഈ പോയിന്റ് ഉത്ഭവവുമായി ബന്ധിപ്പിച്ച് യൂണിറ്റ് സർക്കിളുമായി തത്ഫലമായുണ്ടാകുന്ന സെഗ്മെന്റിന്റെ വിഭജന പോയിന്റ് അടയാളപ്പെടുത്തുക. 5. ഒരു സർക്കിളിന്റെ ഒരു ആർക്ക് തിരഞ്ഞെടുക്കുക, അതിന്റെ എല്ലാ ബിന്ദുക്കൾക്കും ടാൻജെന്റ് ലൈനിൽ ഓർഡിനേറ്റ് കുറവാണ്എ
.
6. ട്രാവേഴ്സലിന്റെ ദിശ സൂചിപ്പിക്കുകയും ഫംഗ്ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്ൻ കണക്കിലെടുത്ത് ഉത്തരം എഴുതുകയും ചെയ്യുക, ഒരു കാലയളവ് ചേർക്കുകπn
,
ഏറ്റവും ലളിതമായ സമവാക്യങ്ങളിലേക്കുള്ള പരിഹാരങ്ങളുടെ ഗ്രാഫിക് വ്യാഖ്യാനവും പൊതു രൂപത്തിൽ അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സൂത്രവാക്യങ്ങളും അനുബന്ധത്തിൽ സൂചിപ്പിച്ചിരിക്കുന്നു (അനുബന്ധങ്ങൾ 1 ഉം 2 ഉം). ഉദാഹരണം 1.
അസമത്വം പരിഹരിക്കുക യൂണിറ്റ് സർക്കിളിൽ ഒരു നേർരേഖ വരയ്ക്കുക എല്ലാ അർത്ഥങ്ങളുംവൈ
ഇടവേളയിൽ NM കൂടുതലാണ്
, AMB ആർക്കിന്റെ എല്ലാ പോയിന്റുകളും ഈ അസമത്വത്തെ തൃപ്തിപ്പെടുത്തുന്നു. എല്ലാ ഭ്രമണ കോണുകളിലും, വലുത് ചിത്രം.1 അങ്ങനെ, അസമത്വത്തിനുള്ള പരിഹാരം ഇടവേളയിലെ എല്ലാ മൂല്യങ്ങളും ആയിരിക്കും ആ. ഉത്തരം: 1.2 ഗ്രാഫിക്കൽ രീതി
പ്രായോഗികമായി, ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഗ്രാഫിക്കൽ രീതി പലപ്പോഴും ഉപയോഗപ്രദമാകും. അസമത്വത്തിന്റെ ഉദാഹരണം ഉപയോഗിച്ച് രീതിയുടെ സാരാംശം നമുക്ക് പരിഗണിക്കാം 1. വാദം സങ്കീർണ്ണമാണെങ്കിൽ (വ്യത്യസ്‌തമാണ്എക്സ്
), എന്നിട്ട് അത് മാറ്റിസ്ഥാപിക്കുകടി
.
2. ഞങ്ങൾ ഒരു കോർഡിനേറ്റ് തലത്തിൽ നിർമ്മിക്കുന്നുടോയ്
ഫംഗ്ഷൻ ഗ്രാഫുകൾ 3. ഞങ്ങൾ അങ്ങനെ കണ്ടെത്തുന്നുഗ്രാഫുകളുടെ വിഭജനത്തിന്റെ രണ്ട് അടുത്തുള്ള പോയിന്റുകൾ, അതിനിടയിൽസൈൻ തരംഗംസ്ഥിതി ചെയ്യുന്നത്ഉയർന്നത്
ഋജുവായത് 4. വാദത്തിന് ഇരട്ട അസമത്വം എഴുതുകടി
, കോസൈൻ കാലയളവ് കണക്കിലെടുത്ത് (ടി
കണ്ടെത്തിയ അബ്സിസ്സകൾക്കിടയിലായിരിക്കും). 5. ഒരു റിവേഴ്സ് സബ്സ്റ്റിറ്റ്യൂഷൻ ഉണ്ടാക്കുക (യഥാർത്ഥ ആർഗ്യുമെന്റിലേക്ക് മടങ്ങുക) മൂല്യം പ്രകടിപ്പിക്കുകഎക്സ്
ഇരട്ട അസമത്വത്തിൽ നിന്ന്, ഞങ്ങൾ ഉത്തരം ഒരു സംഖ്യാ ഇടവേളയുടെ രൂപത്തിൽ എഴുതുന്നു. ഉദാഹരണം 2.
അസമത്വം പരിഹരിക്കുക: . ഗ്രാഫിക്കൽ രീതി ഉപയോഗിച്ച് അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ, ഫംഗ്ഷനുകളുടെ ഗ്രാഫുകൾ കഴിയുന്നത്ര കൃത്യമായി നിർമ്മിക്കേണ്ടത് ആവശ്യമാണ്. നമുക്ക് അസമത്വത്തെ രൂപത്തിലേക്ക് പരിവർത്തനം ചെയ്യാം: ഒരു കോർഡിനേറ്റ് സിസ്റ്റത്തിൽ ഫംഗ്ഷനുകളുടെ ഗ്രാഫുകൾ നിർമ്മിക്കാം ചിത്രം.2 പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകൾ പോയിന്റിൽ വിഭജിക്കുന്നുഎ
കോർഡിനേറ്റുകൾക്കൊപ്പം ഉത്തരം: 1.3 ബീജഗണിത രീതി
മിക്കപ്പോഴും, യഥാർത്ഥ ത്രികോണമിതി അസമത്വത്തെ നന്നായി തിരഞ്ഞെടുത്ത ഒരു പകരക്കാരനായി ബീജഗണിത (യുക്തിപരമോ യുക്തിരഹിതമോ) അസമത്വത്തിലേക്ക് ചുരുക്കാൻ കഴിയും. ഈ രീതി ഒരു അസമത്വത്തെ പരിവർത്തനം ചെയ്യുക, ഒരു പകരക്കാരനെ അവതരിപ്പിക്കുക അല്ലെങ്കിൽ ഒരു വേരിയബിൾ മാറ്റിസ്ഥാപിക്കുക എന്നിവ ഉൾപ്പെടുന്നു. ഈ രീതിയുടെ പ്രയോഗത്തിന്റെ പ്രത്യേക ഉദാഹരണങ്ങൾ നോക്കാം. ഉദാഹരണം 3.
ഏറ്റവും ലളിതമായ രൂപത്തിലേക്ക് കുറയ്ക്കൽ ചിത്രം.3 ഉത്തരം: ഉദാഹരണം 4.
അസമത്വം പരിഹരിക്കുക: ODZ: സൂത്രവാക്യങ്ങൾ ഉപയോഗിക്കുന്നു: അസമത്വം ഫോമിൽ എഴുതാം: അല്ലെങ്കിൽ, വിശ്വസിക്കുന്നു ഇടവേള രീതി ഉപയോഗിച്ച് അവസാന അസമത്വം പരിഹരിക്കുന്നതിലൂടെ, ഞങ്ങൾക്ക് ലഭിക്കുന്നത്: ചിത്രം.4 ചിത്രം.5 ഉത്തരം: 1.4 ഇടവേള രീതി
ഇടവേള രീതി ഉപയോഗിച്ച് ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പൊതു സ്കീം: ത്രികോണമിതി സൂത്രവാക്യങ്ങൾ ഉപയോഗിക്കുന്ന ഘടകം. ഫംഗ്ഷന്റെ വിച്ഛേദിക്കുന്ന പോയിന്റുകളും പൂജ്യങ്ങളും കണ്ടെത്തി അവയെ സർക്കിളിൽ സ്ഥാപിക്കുക. ഏതെങ്കിലും പോയിന്റ് എടുക്കുകTO
(എന്നാൽ നേരത്തെ കണ്ടെത്തിയില്ല) കൂടാതെ ഉൽപ്പന്നത്തിന്റെ അടയാളം കണ്ടെത്തുക. ഉൽപ്പന്നം പോസിറ്റീവ് ആണെങ്കിൽ, യൂണിറ്റ് സർക്കിളിന് പുറത്ത് കോണുമായി ബന്ധപ്പെട്ട കിരണത്തിൽ ഒരു പോയിന്റ് സ്ഥാപിക്കുക. അല്ലെങ്കിൽ, പോയിന്റ് സർക്കിളിനുള്ളിൽ വയ്ക്കുക. ഒരു ബിന്ദു ഇരട്ട സംഖ്യയിൽ സംഭവിക്കുകയാണെങ്കിൽ, അതിനെ ഇരട്ട ഗുണനത്തിന്റെ ഒരു ബിന്ദു എന്നും ഒറ്റ സംഖ്യയാണെങ്കിൽ അതിനെ ഒറ്റ ഗുണനത്തിന്റെ ഒരു ബിന്ദു എന്നും വിളിക്കുന്നു. ഇനിപ്പറയുന്ന രീതിയിൽ ആർക്കുകൾ വരയ്ക്കുക: ഒരു പോയിന്റിൽ നിന്ന് ആരംഭിക്കുകTO
, അടുത്ത പോയിന്റ് വിചിത്ര ഗുണിതമാണെങ്കിൽ, ഈ ഘട്ടത്തിൽ ആർക്ക് വൃത്തത്തെ വിഭജിക്കുന്നു, എന്നാൽ പോയിന്റ് ഇരട്ട ഗുണിതമാണെങ്കിൽ, അത് വിഭജിക്കില്ല. വൃത്തത്തിന് പിന്നിലെ കമാനങ്ങൾ പോസിറ്റീവ് ഇടവേളകളാണ്; സർക്കിളിനുള്ളിൽ നെഗറ്റീവ് സ്പേസുകളുണ്ട്. ഉദാഹരണം 5.
അസമത്വം പരിഹരിക്കുക ആദ്യ പരമ്പരയിലെ പോയിന്റുകൾ: രണ്ടാമത്തെ പരമ്പരയിലെ പോയിന്റുകൾ: ഓരോ പോയിന്റും ഒറ്റസംഖ്യയുടെ തവണ സംഭവിക്കുന്നു, അതായത്, എല്ലാ പോയിന്റുകളും ഒറ്റ ഗുണിതമാണ്. ഉൽപ്പന്നത്തിന്റെ അടയാളം നമുക്ക് കണ്ടെത്താം അരി. 6 ഉത്തരം: ഉദാഹരണം 6
. അസമത്വം പരിഹരിക്കുക.
പരിഹാരം:
പദപ്രയോഗത്തിന്റെ പൂജ്യങ്ങൾ കണ്ടെത്താം .
സ്വീകരിക്കുകaeഎം :
യൂണിറ്റ് സർക്കിൾ ശ്രേണി മൂല്യങ്ങളിൽഎക്സ്
1
ഡോട്ടുകളാൽ പ്രതിനിധീകരിക്കുന്നു ഇനി നമ്പർ പറയാം അതിനാൽ, പൂർണ്ണവിരാമംഎ
ആംഗിൾ രൂപപ്പെടുന്ന കിരണത്തിൽ തിരഞ്ഞെടുക്കണം ഇപ്പോൾ പോയിന്റിൽ നിന്ന്എ
അടയാളപ്പെടുത്തിയ എല്ലാ പോയിന്റുകളിലേക്കും തുടർച്ചയായി ഒരു തരംഗമായ തുടർച്ചയായ വര വരയ്ക്കുക. ഒപ്പം പോയിന്റുകളിലും ചിത്രം.7 അന്തിമ ഉത്തരം: കുറിപ്പ്.
യൂണിറ്റ് സർക്കിളിൽ അടയാളപ്പെടുത്തിയിരിക്കുന്ന എല്ലാ ബിന്ദുക്കൾക്കും ചുറ്റും ഒരു തരംഗ രേഖ പോയാൽ, പോയിന്റിലേക്ക് മടങ്ങാൻ കഴിയില്ലഎ
,
"നിയമവിരുദ്ധമായ" സ്ഥലത്ത് സർക്കിൾ കടക്കാതെ, ഇതിനർത്ഥം പരിഹാരത്തിൽ ഒരു പിശക് സംഭവിച്ചു എന്നാണ്, അതായത്, ഒറ്റസംഖ്യയുടെ വേരുകൾ നഷ്‌ടപ്പെട്ടു. ഉത്തരം:
.
§2. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു കൂട്ടം പ്രശ്നങ്ങൾ
ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കാനുള്ള സ്കൂൾ കുട്ടികളുടെ കഴിവ് വികസിപ്പിക്കുന്ന പ്രക്രിയയിൽ, 3 ഘട്ടങ്ങളും വേർതിരിച്ചറിയാൻ കഴിയും. 1. തയ്യാറെടുപ്പ്, 2. ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കാനുള്ള കഴിവ് വികസിപ്പിക്കൽ; 3. മറ്റ് തരത്തിലുള്ള ത്രികോണമിതി അസമത്വങ്ങളുടെ ആമുഖം. അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിന് ഒരു ത്രികോണമിതി സർക്കിൾ അല്ലെങ്കിൽ ഗ്രാഫ് ഉപയോഗിക്കാനുള്ള കഴിവ് സ്കൂൾ കുട്ടികളിൽ വികസിപ്പിക്കേണ്ടത് ആവശ്യമാണ് എന്നതാണ് തയ്യാറെടുപ്പ് ഘട്ടത്തിന്റെ ലക്ഷ്യം, അതായത്: ഫോമിന്റെ ലളിതമായ അസമത്വങ്ങൾ പരിഹരിക്കാനുള്ള കഴിവ് നമ്പർ സർക്കിളിന്റെ ആർക്കുകൾക്കോ ഫംഗ്ഷനുകളുടെ ഗ്രാഫുകളുടെ ആർക്കുകൾക്കോ വേണ്ടി ഇരട്ട അസമത്വങ്ങൾ നിർമ്മിക്കാനുള്ള കഴിവ്; ത്രികോണമിതി പദപ്രയോഗങ്ങളുടെ വിവിധ പരിവർത്തനങ്ങൾ നടത്താനുള്ള കഴിവ്. ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ സവിശേഷതകളെക്കുറിച്ചുള്ള സ്കൂൾ കുട്ടികളുടെ അറിവ് ചിട്ടപ്പെടുത്തുന്ന പ്രക്രിയയിൽ ഈ ഘട്ടം നടപ്പിലാക്കാൻ ശുപാർശ ചെയ്യുന്നു. പ്രധാന മാർഗ്ഗങ്ങൾ വിദ്യാർത്ഥികൾക്ക് വാഗ്ദാനം ചെയ്യുന്നതും ഒരു അധ്യാപകന്റെ മാർഗ്ഗനിർദ്ദേശത്തിലോ സ്വതന്ത്രമായോ നിർവ്വഹിക്കുന്ന ജോലികളും ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിൽ വികസിപ്പിച്ച കഴിവുകളും ആകാം. അത്തരം ജോലികളുടെ ഉദാഹരണങ്ങൾ ഇതാ: 1
. യൂണിറ്റ് സർക്കിളിൽ ഒരു പോയിന്റ് അടയാളപ്പെടുത്തുക .
2.
കോർഡിനേറ്റ് തലത്തിന്റെ ഏത് പാദത്തിലാണ് പോയിന്റ് സ്ഥിതിചെയ്യുന്നത്? 3.
ത്രികോണമിതി സർക്കിളിൽ പോയിന്റുകൾ അടയാളപ്പെടുത്തുക 4.
എക്സ്പ്രഷൻ ത്രികോണമിതി ഫംഗ്ഷനുകളിലേക്ക് പരിവർത്തനം ചെയ്യുകഐക്വാർട്ടേഴ്സ്. എ) 5.
ആർക്ക് എംആർ നൽകിയിരിക്കുന്നു.എം
- മധ്യഐ-ആം പാദം,ആർ
- മധ്യIIപാദം. ഒരു വേരിയബിളിന്റെ മൂല്യം പരിമിതപ്പെടുത്തുകടി
ഇതിനായി: (ഇരട്ട അസമത്വം ഉണ്ടാക്കുക) a) ആർക്ക് MR; ബി) ആർഎം ആർക്കുകൾ. 6.
ഗ്രാഫിന്റെ തിരഞ്ഞെടുത്ത വിഭാഗങ്ങൾക്കുള്ള ഇരട്ട അസമത്വം എഴുതുക: അരി. 1 7.
അസമത്വങ്ങൾ പരിഹരിക്കുക 8.
എക്സ്പ്രഷൻ പരിവർത്തനം ചെയ്യുക
.
ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പഠനത്തിന്റെ രണ്ടാം ഘട്ടത്തിൽ, വിദ്യാർത്ഥി പ്രവർത്തനങ്ങൾ സംഘടിപ്പിക്കുന്നതിനുള്ള രീതിശാസ്ത്രവുമായി ബന്ധപ്പെട്ട ഇനിപ്പറയുന്ന ശുപാർശകൾ ഞങ്ങൾക്ക് വാഗ്ദാനം ചെയ്യാൻ കഴിയും. ഈ സാഹചര്യത്തിൽ, ലളിതമായ ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ രൂപീകരിച്ച ഒരു ത്രികോണമിതി സർക്കിൾ അല്ലെങ്കിൽ ഗ്രാഫ് ഉപയോഗിച്ച് പ്രവർത്തിക്കുന്നതിൽ വിദ്യാർത്ഥികളുടെ നിലവിലുള്ള കഴിവുകളിൽ ശ്രദ്ധ കേന്ദ്രീകരിക്കേണ്ടത് ആവശ്യമാണ്. ഒന്നാമതായി, ഫോമിന്റെ അസമത്വത്തിലേക്ക് തിരിഞ്ഞ് ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു പൊതു രീതി നേടുന്നതിന് ഒരാൾക്ക് പ്രചോദിപ്പിക്കാൻ കഴിയും. രണ്ടാമതായി, ചുമതല പൂർത്തിയാക്കുന്നതിനുള്ള വ്യത്യസ്ത വഴികളിലേക്ക് അധ്യാപകൻ വിദ്യാർത്ഥികളുടെ ശ്രദ്ധ ആകർഷിക്കണം, അസമത്വം ഗ്രാഫിക്കലായും ഒരു ത്രികോണമിതി സർക്കിൾ ഉപയോഗിച്ചും പരിഹരിക്കുന്നതിനുള്ള ഉചിതമായ ഉദാഹരണം നൽകുക. അസമത്വത്തിനുള്ള ഇനിപ്പറയുന്ന പരിഹാരങ്ങൾ നമുക്ക് പരിഗണിക്കാം 1. യൂണിറ്റ് സർക്കിൾ ഉപയോഗിച്ച് അസമത്വം പരിഹരിക്കുന്നു. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ആദ്യ പാഠത്തിൽ, ഞങ്ങൾ വിദ്യാർത്ഥികൾക്ക് വിശദമായ പരിഹാര അൽഗോരിതം വാഗ്ദാനം ചെയ്യും, അത് ഘട്ടം ഘട്ടമായുള്ള അവതരണത്തിൽ അസമത്വം പരിഹരിക്കുന്നതിന് ആവശ്യമായ എല്ലാ അടിസ്ഥാന കഴിവുകളും പ്രതിഫലിപ്പിക്കുന്നു. ഘട്ടം 1.നമുക്ക് ഒരു യൂണിറ്റ് സർക്കിൾ വരച്ച് ഓർഡിനേറ്റ് അക്ഷത്തിൽ ഒരു പോയിന്റ് അടയാളപ്പെടുത്താം ഘട്ടം 2.ഈ നേർരേഖ വൃത്തത്തെ രണ്ട് കമാനങ്ങളായി വിഭജിച്ചു. കൂടുതൽ സൈനുള്ള സംഖ്യകളെ ചിത്രീകരിക്കുന്ന ഒന്ന് നമുക്ക് തിരഞ്ഞെടുക്കാം അരി. 2 ഘട്ടം 3.അടയാളപ്പെടുത്തിയ ആർക്കിന്റെ അറ്റങ്ങളിൽ ഒന്ന് തിരഞ്ഞെടുക്കുക. യൂണിറ്റ് സർക്കിളിന്റെ ഈ പോയിന്റ് പ്രതിനിധീകരിക്കുന്ന സംഖ്യകളിൽ ഒന്ന് എഴുതാം ഘട്ടം 4.തിരഞ്ഞെടുത്ത ആർക്കിന്റെ രണ്ടാമത്തെ അറ്റവുമായി ബന്ധപ്പെട്ട നമ്പർ തിരഞ്ഞെടുക്കുന്നതിന്, നാമകരണം ചെയ്ത അറ്റത്ത് നിന്ന് മറ്റൊന്നിലേക്ക് ഞങ്ങൾ ഈ ആർക്കിലൂടെ "നടക്കുന്നു". അതേ സമയം, എതിർ ഘടികാരദിശയിൽ നീങ്ങുമ്പോൾ, നമ്മൾ കടന്നുപോകുന്ന സംഖ്യകൾ വർദ്ധിക്കും (എതിർ ദിശയിൽ നീങ്ങുമ്പോൾ, അക്കങ്ങൾ കുറയും). അടയാളപ്പെടുത്തിയ ആർക്കിന്റെ രണ്ടാം അറ്റത്ത് യൂണിറ്റ് സർക്കിളിൽ ചിത്രീകരിച്ചിരിക്കുന്ന നമ്പർ നമുക്ക് എഴുതാം അങ്ങനെ ആ അസമത്വം നാം കാണുന്നു ഡ്രോയിംഗ് ശ്രദ്ധാപൂർവ്വം പരിശോധിക്കാനും അസമത്വത്തിനുള്ള എല്ലാ പരിഹാരങ്ങളും എന്തുകൊണ്ടാണെന്ന് കണ്ടെത്താനും വിദ്യാർത്ഥികളോട് ആവശ്യപ്പെടണം അരി. 3 കോസൈൻ പ്രവർത്തനത്തിനുള്ള അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ, ഓർഡിനേറ്റ് അക്ഷത്തിന് സമാന്തരമായി ഞങ്ങൾ ഒരു നേർരേഖ വരയ്ക്കുന്നു എന്ന വസ്തുതയിലേക്ക് വിദ്യാർത്ഥികളുടെ ശ്രദ്ധ ആകർഷിക്കേണ്ടത് ആവശ്യമാണ്. അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഗ്രാഫിക്കൽ രീതി. ഞങ്ങൾ ഗ്രാഫുകൾ നിർമ്മിക്കുന്നു അരി. 4 അപ്പോൾ നമ്മൾ സമവാക്യം എഴുതുന്നു (നൽകുന്നഎൻ
0, 1, 2 മൂല്യങ്ങൾ, സമാഹരിച്ച സമവാക്യത്തിന്റെ മൂന്ന് വേരുകൾ ഞങ്ങൾ കണ്ടെത്തുന്നു). മൂല്യങ്ങൾ അരി. 5 സംഗഹിക്കുക. അസമത്വം പരിഹരിക്കാൻ മൂന്നാമതായി, ഗ്രാഫിക്കായി പരിഹരിക്കുമ്പോൾ, അനുബന്ധ ത്രികോണമിതി അസമത്വത്തിന്റെ വേരുകളുടെ ഗണത്തെക്കുറിച്ചുള്ള വസ്തുത വളരെ വ്യക്തമായി സ്ഥിരീകരിക്കുന്നു. അരി. 6 അസമത്വത്തിനുള്ള പരിഹാരമായ ടേൺ, ത്രികോണമിതി പ്രവർത്തനത്തിന്റെ കാലഘട്ടത്തിന് തുല്യമായ അതേ ഇടവേളയിലൂടെ ആവർത്തിക്കുന്നുവെന്ന് വിദ്യാർത്ഥികളോട് പ്രകടിപ്പിക്കേണ്ടത് ആവശ്യമാണ്. സൈൻ ഫംഗ്ഷന്റെ ഗ്രാഫിന് സമാനമായ ഒരു ചിത്രീകരണം നിങ്ങൾക്ക് പരിഗണിക്കാം. നാലാമതായി, ത്രികോണമിതി പ്രവർത്തനങ്ങളുടെ ആകെത്തുക (വ്യത്യാസം) ഒരു ഉൽപ്പന്നമാക്കി മാറ്റുന്നതിനുള്ള വിദ്യാർത്ഥികളുടെ സാങ്കേതികതകൾ അപ്‌ഡേറ്റ് ചെയ്യുന്നതും ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിൽ ഈ സാങ്കേതിക വിദ്യകളുടെ പങ്കിലേക്ക് വിദ്യാർത്ഥികളുടെ ശ്രദ്ധ ആകർഷിക്കുന്നതും ഉചിതമാണ്. അധ്യാപകൻ നിർദ്ദേശിച്ച ജോലികൾ വിദ്യാർത്ഥികളുടെ സ്വതന്ത്രമായി പൂർത്തിയാക്കുന്നതിലൂടെ അത്തരം ജോലികൾ സംഘടിപ്പിക്കാൻ കഴിയും, അവയിൽ ഇനിപ്പറയുന്നവ ഞങ്ങൾ ഹൈലൈറ്റ് ചെയ്യുന്നു: അഞ്ചാമതായി, ഓരോ ലളിതമായ ത്രികോണമിതി അസമത്വത്തിനും ഒരു ഗ്രാഫ് അല്ലെങ്കിൽ ഒരു ത്രികോണമിതി വൃത്തം ഉപയോഗിച്ച് പരിഹാരം ചിത്രീകരിക്കാൻ വിദ്യാർത്ഥികൾ ആവശ്യപ്പെടണം. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുമ്പോൾ, തന്നിരിക്കുന്ന അസമത്വത്തിനുള്ള പരിഹാരങ്ങളുടെ ഒരു കൂട്ടം രേഖപ്പെടുത്തുന്നതിനുള്ള വളരെ സൗകര്യപ്രദമായ മാർഗ്ഗമായി അനുബന്ധ ചിത്രീകരണം വർത്തിക്കുന്നതിനാൽ, അതിന്റെ പ്രയോജനം, പ്രത്യേകിച്ച് സർക്കിളിന്റെ ഉപയോഗത്തിൽ നിങ്ങൾ തീർച്ചയായും ശ്രദ്ധിക്കണം. ഇനിപ്പറയുന്ന സ്കീം അനുസരിച്ച് ഏറ്റവും ലളിതമല്ലാത്ത ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികളിലേക്ക് വിദ്യാർത്ഥികളെ പരിചയപ്പെടുത്തുന്നത് ഉചിതമാണ്: ഒരു നിർദ്ദിഷ്ട ത്രികോണമിതി അസമത്വത്തിലേക്ക് തിരിയുന്നു, അനുബന്ധ ത്രികോണമിതി സമവാക്യം സംയുക്ത തിരയലിലേക്ക് (അധ്യാപകൻ - വിദ്യാർത്ഥികൾ) തിരിയുന്നു. സമാന തരത്തിലുള്ള മറ്റ് അസമത്വങ്ങൾക്കുള്ള രീതി കണ്ടെത്തി. ത്രികോണമിതിയെക്കുറിച്ചുള്ള വിദ്യാർത്ഥികളുടെ അറിവ് ചിട്ടപ്പെടുത്തുന്നതിന്, അത്തരം അസമത്വങ്ങൾ പ്രത്യേകം തിരഞ്ഞെടുക്കാൻ ഞങ്ങൾ ശുപാർശ ചെയ്യുന്നു, അതിന്റെ പരിഹാരത്തിന് അത് പരിഹരിക്കുന്ന പ്രക്രിയയിൽ നടപ്പിലാക്കാൻ കഴിയുന്ന വിവിധ പരിവർത്തനങ്ങൾ ആവശ്യമാണ്, കൂടാതെ അവരുടെ സവിശേഷതകളിൽ വിദ്യാർത്ഥികളുടെ ശ്രദ്ധ കേന്ദ്രീകരിക്കുകയും ചെയ്യുന്നു. ഉൽപ്പാദനപരമായ അസമത്വങ്ങൾ എന്ന നിലയിൽ നമുക്ക് നിർദ്ദേശിക്കാം, ഉദാഹരണത്തിന്, ഇനിപ്പറയുന്നവ: ഉപസംഹാരമായി, ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു കൂട്ടം പ്രശ്നങ്ങളുടെ ഒരു ഉദാഹരണം ഞങ്ങൾ നൽകുന്നു. 1. അസമത്വങ്ങൾ പരിഹരിക്കുക: എ) b) 5. അസമത്വങ്ങൾക്കുള്ള എല്ലാ പരിഹാരങ്ങളും കണ്ടെത്തുക: എ) ;
b) ;
വി) ജി) d) 6. അസമത്വങ്ങൾ പരിഹരിക്കുക: എ) ;
b) ;
വി) ; ജി) d) ; ഇ) ; ഒപ്പം) 7. അസമത്വങ്ങൾ പരിഹരിക്കുക: എ) b) ;
വി) ; ജി) . 8. അസമത്വങ്ങൾ പരിഹരിക്കുക: എ) ;
b) ;
വി) ; ജി) d) ഇ) ; ഒപ്പം) h) . വിപുലമായ തലത്തിൽ ഗണിതശാസ്ത്രം പഠിക്കുന്ന വിദ്യാർത്ഥികൾക്ക് ടാസ്‌ക്കുകൾ 6 ഉം 7 ഉം, ഗണിതത്തെക്കുറിച്ചുള്ള വിപുലമായ പഠനമുള്ള ക്ലാസുകളിലെ വിദ്യാർത്ഥികൾക്ക് ടാസ്‌ക് 8 ഉം നൽകുന്നത് ഉചിതമാണ്. §3. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പ്രത്യേക രീതികൾ
ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള പ്രത്യേക രീതികൾ - അതായത്, ത്രികോണമിതി സമവാക്യങ്ങൾ പരിഹരിക്കാൻ മാത്രം ഉപയോഗിക്കാവുന്ന രീതികൾ. ഈ രീതികൾ ത്രികോണമിതി ഫംഗ്ഷനുകളുടെ ഗുണവിശേഷതകളുടെ ഉപയോഗത്തെയും വിവിധ ത്രികോണമിതി സൂത്രവാക്യങ്ങളുടെയും ഐഡന്റിറ്റികളുടെയും ഉപയോഗത്തെ അടിസ്ഥാനമാക്കിയുള്ളതാണ്. 3.1 സെക്ടർ രീതി
ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സെക്ടർ രീതി നമുക്ക് പരിഗണിക്കാം. ഫോമിലെ അസമത്വങ്ങൾ പരിഹരിക്കുന്നു ഇടവേള രീതിയിൽ, ഫോമിന്റെ ന്യൂമറേറ്ററിന്റെയും ഡിനോമിനേറ്ററിന്റെയും ഓരോ രേഖീയ ഘടകവും ഇനിപ്പറയുന്നവ ഓർമ്മിക്കേണ്ടതാണ്: a) രൂപത്തിന്റെ ഘടകങ്ങൾ ബി) ഫോമിന്റെ ഘടകങ്ങൾ ഉദാഹരണം 1.
അസമത്വങ്ങൾ പരിഹരിക്കുക: a) 3.2 കേന്ദ്രീകൃത സർക്കിൾ രീതി
ഈ രീതി യുക്തിസഹമായ അസമത്വങ്ങളുടെ സിസ്റ്റങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സമാന്തര സംഖ്യ അച്ചുതണ്ട് രീതിയുടെ ഒരു അനലോഗ് ആണ്. അസമത്വ വ്യവസ്ഥയുടെ ഒരു ഉദാഹരണം നോക്കാം. ഉദാഹരണം 5.
ലളിതമായ ത്രികോണമിതി അസമത്വങ്ങളുടെ ഒരു സിസ്റ്റം പരിഹരിക്കുക ആദ്യം, ഞങ്ങൾ ഓരോ അസമത്വവും പ്രത്യേകം പരിഹരിക്കുന്നു (ചിത്രം 5). ചിത്രത്തിന്റെ മുകളിൽ വലത് കോണിൽ ഏത് ആർഗ്യുമെന്റിനാണ് ത്രികോണമിതി സർക്കിൾ പരിഗണിക്കുന്നതെന്ന് ഞങ്ങൾ സൂചിപ്പിക്കും. ചിത്രം.5 അടുത്തതായി, വാദത്തിനായി ഞങ്ങൾ കേന്ദ്രീകൃത സർക്കിളുകളുടെ ഒരു സംവിധാനം നിർമ്മിക്കുന്നുഎക്സ്
. ആദ്യത്തെ അസമത്വത്തിന്റെ പരിഹാരമനുസരിച്ച് ഞങ്ങൾ ഒരു വൃത്തം വരച്ച് ഷേഡ് ചെയ്യുന്നു, തുടർന്ന് ഞങ്ങൾ ഒരു വലിയ ആരത്തിന്റെ ഒരു വൃത്തം വരച്ച് രണ്ടാമത്തേതിന്റെ പരിഹാരത്തിന് അനുസരിച്ച് ഷേഡ് ചെയ്യുന്നു, തുടർന്ന് മൂന്നാമത്തെ അസമത്വത്തിനും അടിസ്ഥാന വൃത്തത്തിനും ഞങ്ങൾ ഒരു വൃത്തം നിർമ്മിക്കുന്നു. സിസ്റ്റത്തിന്റെ മധ്യഭാഗത്ത് നിന്ന് ആർക്കുകളുടെ അറ്റങ്ങളിലൂടെ ഞങ്ങൾ കിരണങ്ങൾ വരയ്ക്കുന്നു, അങ്ങനെ അവ എല്ലാ സർക്കിളുകളും വിഭജിക്കുന്നു. അടിസ്ഥാന സർക്കിളിൽ ഞങ്ങൾ ഒരു പരിഹാരം ഉണ്ടാക്കുന്നു (ചിത്രം 6). ചിത്രം.6 ഉത്തരം:
ഉപസംഹാരം
കോഴ്സ് ഗവേഷണത്തിന്റെ എല്ലാ ലക്ഷ്യങ്ങളും പൂർത്തിയായി. സൈദ്ധാന്തിക മെറ്റീരിയൽ ചിട്ടപ്പെടുത്തിയിരിക്കുന്നു: ത്രികോണമിതി അസമത്വങ്ങളുടെ പ്രധാന തരങ്ങളും അവ പരിഹരിക്കുന്നതിനുള്ള പ്രധാന രീതികളും നൽകിയിരിക്കുന്നു (ഗ്രാഫിക്കൽ, ബീജഗണിതം, ഇടവേളകളുടെ രീതി, സെക്ടറുകൾ, കേന്ദ്രീകൃത സർക്കിളുകളുടെ രീതി). ഓരോ രീതിക്കും അസമത്വം പരിഹരിക്കുന്നതിനുള്ള ഒരു ഉദാഹരണം നൽകി. സൈദ്ധാന്തിക ഭാഗത്തിന് ശേഷം പ്രായോഗിക ഭാഗം. ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഒരു കൂട്ടം ജോലികൾ ഇതിൽ അടങ്ങിയിരിക്കുന്നു. ഈ കോഴ്സ് വർക്ക് വിദ്യാർത്ഥികൾക്ക് സ്വതന്ത്ര ജോലിക്കായി ഉപയോഗിക്കാം. സ്കൂൾ കുട്ടികൾക്ക് ഈ വിഷയത്തിന്റെ വൈദഗ്ധ്യത്തിന്റെ നിലവാരം പരിശോധിക്കാനും വ്യത്യസ്ത സങ്കീർണ്ണതയുടെ ജോലികൾ പൂർത്തിയാക്കാനും കഴിയും. ഈ വിഷയത്തിൽ പ്രസക്തമായ സാഹിത്യം പഠിച്ച ശേഷം, ബീജഗണിതത്തിന്റെയും പ്രാഥമിക വിശകലനത്തിന്റെയും സ്കൂൾ കോഴ്സിലെ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കാനുള്ള കഴിവും നൈപുണ്യവും വളരെ പ്രധാനമാണെന്ന് നമുക്ക് വ്യക്തമായും നിഗമനം ചെയ്യാം, ഇതിന്റെ വികസനത്തിന് ഗണിതശാസ്ത്ര അധ്യാപകന്റെ ഭാഗത്തുനിന്ന് കാര്യമായ പരിശ്രമം ആവശ്യമാണ്. അതിനാൽ, ഈ കൃതി ഗണിതശാസ്ത്ര അധ്യാപകർക്ക് ഉപയോഗപ്രദമാകും, കാരണം "ത്രികോണമിതി അസമത്വങ്ങൾ" എന്ന വിഷയത്തിൽ വിദ്യാർത്ഥികളുടെ പരിശീലനം ഫലപ്രദമായി സംഘടിപ്പിക്കുന്നത് സാധ്യമാക്കുന്നു. അന്തിമ യോഗ്യതാ ജോലിയിലേക്ക് വിപുലീകരിച്ചുകൊണ്ട് ഗവേഷണം തുടരാം.
ഉപയോഗിച്ച സാഹിത്യങ്ങളുടെ പട്ടിക
ബോഗോമോലോവ്, എൻ.വി. ഗണിതശാസ്ത്രത്തിലെ പ്രശ്നങ്ങളുടെ ശേഖരണം [ടെക്സ്റ്റ്] / എൻ.വി. ബോഗോമോലോവ്. - എം.: ബസ്റ്റാർഡ്, 2009. - 206 പേ. വൈഗോഡ്സ്കി, എം.യാ. പ്രാഥമിക ഗണിതത്തിന്റെ കൈപ്പുസ്തകം [ടെക്സ്റ്റ്] / M.Ya. വൈഗോഡ്സ്കി. - എം.: ബസ്റ്റാർഡ്, 2006. - 509 പേ. Zhurbenko, L.N. ഉദാഹരണങ്ങളിലും പ്രശ്നങ്ങളിലുമുള്ള ഗണിതം [ടെക്സ്റ്റ്] / L.N. സുർബെങ്കോ. – എം.: ഇൻഫ്രാ-എം, 2009. – 373 പേ. ഇവാനോവ്, ഒ.എ. സ്കൂൾ കുട്ടികൾക്കും വിദ്യാർത്ഥികൾക്കും അധ്യാപകർക്കും പ്രാഥമിക ഗണിതശാസ്ത്രം [ടെക്സ്റ്റ്] / ഒ.എ. ഇവാനോവ്. – എം.: MTsNMO, 2009. – 384 പേ. കാർപ്പ്, എ.പി. ആൾജിബ്രയെക്കുറിച്ചുള്ള അസൈൻമെന്റുകളും ഗ്രേഡ് 11 ൽ അന്തിമ ആവർത്തനവും സർട്ടിഫിക്കേഷനും സംഘടിപ്പിക്കുന്നതിനുള്ള വിശകലനത്തിന്റെ തുടക്കവും [ടെക്സ്റ്റ്] / എ.പി. കരിമീൻ. - എം.: വിദ്യാഭ്യാസം, 2005. - 79 പേ. കുലാനിൻ, ഇ.ഡി. ഗണിതത്തിലെ 3000 മത്സര പ്രശ്നങ്ങൾ [ടെക്സ്റ്റ്] / ഇ.ഡി. കുലാനിൻ. - എം.: ഐറിസ്-പ്രസ്സ്, 2007. - 624 പേ. ലീബ്സൺ, കെ.എൽ. ഗണിതത്തിലെ പ്രായോഗിക ജോലികളുടെ ശേഖരണം [ടെക്സ്റ്റ്] / കെ.എൽ. ലെയ്ബ്സൺ. - എം.: ബസ്റ്റാർഡ്, 2010. - 182 പേ. എൽബോ, വി.വി. പാരാമീറ്ററുകളുമായുള്ള പ്രശ്നങ്ങളും അവയുടെ പരിഹാരവും. ത്രികോണമിതി: സമവാക്യങ്ങൾ, അസമത്വങ്ങൾ, സിസ്റ്റങ്ങൾ. പത്താം ക്ലാസ് [ടെക്സ്റ്റ്] / വി.വി. കൈമുട്ട്. - എം.: ARKTI, 2008. - 64 പേ. മനോവ, എ.എൻ. ഗണിതം. ഏകീകൃത സംസ്ഥാന പരീക്ഷയ്ക്ക് തയ്യാറെടുക്കുന്നതിനുള്ള എക്സ്പ്രസ് ട്യൂട്ടർ: വിദ്യാർത്ഥി. മാനുവൽ [ടെക്സ്റ്റ്] / എ.എൻ. മനോവ. - റോസ്തോവ്-ഓൺ-ഡോൺ: ഫീനിക്സ്, 2012. - 541 പേ. മൊർഡ്കോവിച്ച്, എ.ജി. ബീജഗണിതവും ഗണിതശാസ്ത്ര വിശകലനത്തിന്റെ തുടക്കവും. 10-11 ഗ്രേഡുകൾ. പൊതു വിദ്യാഭ്യാസ സ്ഥാപനങ്ങളുടെ വിദ്യാർത്ഥികൾക്കുള്ള പാഠപുസ്തകം [ടെക്സ്റ്റ്] / എ.ജി. മൊർഡ്കോവിച്ച്. - എം.: ഐറിസ്-പ്രസ്സ്, 2009. - 201 പേ. നോവിക്കോവ്, എ.ഐ. ത്രികോണമിതി പ്രവർത്തനങ്ങൾ, സമവാക്യങ്ങൾ, അസമത്വങ്ങൾ [ടെക്സ്റ്റ്] / എ.ഐ. നോവിക്കോവ്. - എം.: FIZMATLIT, 2010. - 260 പേ. ഒഗനേഷ്യൻ, വി.എ. സെക്കൻഡറി സ്കൂളിൽ ഗണിതശാസ്ത്രം പഠിപ്പിക്കുന്നതിനുള്ള രീതികൾ: പൊതു രീതിശാസ്ത്രം. പാഠപുസ്തകം ഭൗതികശാസ്ത്ര വിദ്യാർത്ഥികൾക്കുള്ള മാനുവൽ - പായ. വ്യാജം. ped. Inst. [ടെക്സ്റ്റ്] / വി.എ. ഒഗനേഷ്യൻ. - എം.: വിദ്യാഭ്യാസം, 2006. - 368 പേ. ഒലെഹ്നിക്, എസ്.എൻ. സമവാക്യങ്ങളും അസമത്വങ്ങളും. നിലവാരമില്ലാത്ത പരിഹാര രീതികൾ [ടെക്സ്റ്റ്] / എസ്.എൻ. ഒലെഹ്നിക്. - എം.: ഫാക്‌ടോറിയൽ പബ്ലിഷിംഗ് ഹൗസ്, 1997. - 219 പേ. സെവ്ര്യൂക്കോവ്, പി.എഫ്. ത്രികോണമിതി, എക്‌സ്‌പോണൻഷ്യൽ, ലോഗരിഥമിക് സമവാക്യങ്ങളും അസമത്വങ്ങളും [ടെക്സ്റ്റ്] / പി.എഫ്. സെവ്ര്യൂക്കോവ്. - എം.: പൊതു വിദ്യാഭ്യാസം, 2008. - 352 പേ. സെർജീവ്, ഐ.എൻ. ഏകീകൃത സംസ്ഥാന പരീക്ഷ: ഗണിതശാസ്ത്രത്തിലെ ഉത്തരങ്ങളും പരിഹാരങ്ങളുമായി 1000 പ്രശ്നങ്ങൾ. ഗ്രൂപ്പ് സി [ടെക്സ്റ്റ്] / I.N യുടെ എല്ലാ ജോലികളും. സെർജീവ്. - എം.: പരീക്ഷ, 2012. - 301 പേ. സോബോലെവ്, എ.ബി. എലിമെന്ററി മാത്തമാറ്റിക്സ് [ടെക്സ്റ്റ്] / എ.ബി. സോബോലെവ്. - എകറ്റെറിൻബർഗ്: സ്റ്റേറ്റ് എജ്യുക്കേഷണൽ ഇൻസ്റ്റിറ്റ്യൂഷൻ ഓഫ് ഹയർ പ്രൊഫഷണൽ എഡ്യൂക്കേഷൻ USTU-UPI, 2005. - 81 പേ. ഫെങ്കോ, എൽ.എം. അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനും പ്രവർത്തനങ്ങൾ പഠിക്കുന്നതിനുമുള്ള ഇടവേളകളുടെ രീതി [ടെക്സ്റ്റ്] / എൽ.എം. ഫെങ്കോ. - എം.: ബസ്റ്റാർഡ്, 2005. - 124 പേ. ഫ്രീഡ്മാൻ, എൽ.എം. ഗണിതശാസ്ത്രം പഠിപ്പിക്കുന്നതിനുള്ള രീതികളുടെ സൈദ്ധാന്തിക അടിത്തറകൾ [ടെക്സ്റ്റ്] / എൽ.എം. ഫ്രീഡ്മാൻ. - എം.: ബുക്ക് ഹൗസ് "ലിബ്രോക്കോം", 2009. - 248 പേ. അനെക്സ് 1 ലളിതമായ അസമത്വങ്ങൾക്കുള്ള പരിഹാരങ്ങളുടെ ഗ്രാഫിക് വ്യാഖ്യാനം അരി. 1 അരി. 2 ചിത്രം.3 ചിത്രം.4 ചിത്രം.5 ചിത്രം.6 ചിത്രം.7 ചിത്രം.8 അനുബന്ധം 2 ലളിതമായ അസമത്വങ്ങൾക്കുള്ള പരിഹാരങ്ങൾ
, 
മുതലായവ), അവിടെ സാധാരണ അസമത്വം ആദ്യം പരിഹരിക്കപ്പെടുന്നു, തുടർന്ന് രൂപത്തിന്റെ അസമത്വം 
മുതലായവ, അല്ലെങ്കിൽ മറ്റ് രീതികൾ.
ഒരു കാലയളവിൽ അതിന്റെ പരിഹാരം കണ്ടെത്താൻ ഇത് മതിയാകും, അതായത്. ഫംഗ്ഷന്റെ കാലയളവിന് തുല്യമായ ദൈർഘ്യമുള്ള ഏത് സെഗ്‌മെന്റിലുംഎഫ്
x
. അപ്പോൾ യഥാർത്ഥ അസമത്വത്തിനുള്ള പരിഹാരം എല്ലാം കണ്ടെത്തുംx
, അതുപോലെ ഫംഗ്ഷന്റെ കാലയളവുകളുടെ ഏതെങ്കിലും പൂർണ്ണസംഖ്യയാൽ കണ്ടെത്തിയതിൽ നിന്ന് വ്യത്യസ്തമായ മൂല്യങ്ങൾ. ഈ സാഹചര്യത്തിൽ, ഗ്രാഫിക്കൽ രീതി ഉപയോഗിക്കുന്നത് സൗകര്യപ്രദമാണ്.
(
) ഒപ്പം 
.
(
).
.
.
(എൻട്രിയുടെ ഇടതുവശത്തുള്ള സംഖ്യ എല്ലായ്പ്പോഴും വലതുവശത്തുള്ള സംഖ്യയേക്കാൾ കുറവാണ്).
.
, ഇത് എ, ബി പോയിന്റുകളിൽ വൃത്തത്തെ വിഭജിക്കുന്നു.
, എന്നാൽ ചെറുത് 
,
കൂടുതൽ മൂല്യങ്ങൾ ഏറ്റെടുക്കും
(പക്ഷേ ഒന്നിൽ കൂടുതൽ അല്ല).
, അതായത്. 
. ഈ അസമത്വത്തിന് എല്ലാ പരിഹാരങ്ങളും ലഭിക്കുന്നതിന്, ഈ ഇടവേളയുടെ അറ്റത്ത് ചേർത്താൽ മതി 
, എവിടെ 
, അതായത്. 
,
.
മൂല്യങ്ങൾ എന്നത് ശ്രദ്ധിക്കുക 
ഒപ്പം 
സമവാക്യത്തിന്റെ വേരുകളാണ് 
,
;
.
, .
:
ഒപ്പം 
.
. ഈ പോയിന്റുകളുടെ അബ്സിസ്സകൾ ഞങ്ങൾ കണ്ടെത്തുന്നു.
ഒപ്പം 
(ചിത്രം 2).
; 
. ഇടയില് 
ഗ്രാഫ് പോയിന്റുകൾ 
ഗ്രാഫ് പോയിന്റുകൾക്ക് താഴെ 
. പിന്നെ എപ്പോൾ പ്രവർത്തന മൂല്യങ്ങൾ ഒന്നുതന്നെയാണ്. അതുകൊണ്ടാണ് ചെയ്തത് 
.
.
.
(ചിത്രം 3)
, 
.
, 
, 
.
, 
.
ലളിതമായ പരിവർത്തനങ്ങൾക്ക് ശേഷം നമുക്ക് ലഭിക്കും
,
,
.
, യഥാക്രമം 
. തുടർന്ന് ചിത്രത്തിൽ നിന്ന്. 4 പിന്തുടരുന്നു 
, എവിടെ 
.
, 
.
, 
.
.
.
: . യൂണിറ്റ് സർക്കിളിലെ എല്ലാ പോയിന്റുകളും അടയാളപ്പെടുത്താം (ചിത്രം 6):
, 
; 
, 
; 
, 
.
,
;
, 
;
, 
;
, 
;
. പരമ്പരഎക്സ്
2
പോയിന്റുകൾ നൽകുന്നു 
. ഒരു പരമ്പരഎക്സ്
3
ഞങ്ങൾക്ക് രണ്ട് പോയിന്റുകൾ ലഭിക്കും 
. ഒടുവിൽ, പരമ്പരഎക്സ്
4
പോയിന്റുകളെ പ്രതിനിധീകരിക്കും 
. ഈ പോയിന്റുകളെല്ലാം യൂണിറ്റ് സർക്കിളിൽ പ്ലോട്ട് ചെയ്യാം, അവ ഓരോന്നിനും അടുത്തുള്ള പരാൻതീസിസിൽ അതിന്റെ ഗുണിതം സൂചിപ്പിക്കുന്നു.
തുല്യമായിരിക്കും. ചിഹ്നത്തെ അടിസ്ഥാനമാക്കി നമുക്ക് ഒരു എസ്റ്റിമേറ്റ് ഉണ്ടാക്കാം:
ബീം ഉപയോഗിച്ച്ഓ,
യൂണിറ്റ് സർക്കിളിന് പുറത്ത്. (ഓക്സിലറി ബീം എന്നത് ശ്രദ്ധിക്കുകകുറിച്ച്
എ
അത് ഒരു ചിത്രത്തിൽ ചിത്രീകരിക്കേണ്ട ആവശ്യമില്ല. ഡോട്ട്എ
ഏകദേശം തിരഞ്ഞെടുത്തിരിക്കുന്നു.)ഞങ്ങളുടെ ലൈൻ ഒരു ഏരിയയിൽ നിന്ന് മറ്റൊന്നിലേക്ക് പോകുന്നു: അത് യൂണിറ്റ് സർക്കിളിന് പുറത്താണെങ്കിൽ, അത് അതിനുള്ളിലേക്ക് പോകുന്നു. പോയിന്റിനെ സമീപിക്കുന്നു 
, ഈ പോയിന്റിന്റെ ഗുണിതം തുല്യമായതിനാൽ, ലൈൻ ആന്തരിക മേഖലയിലേക്ക് മടങ്ങുന്നു. അതുപോലെ പോയിന്റിൽ 
(ഗുണനിലവാരത്തോടെ) ലൈൻ പുറം മേഖലയിലേക്ക് തിരിയേണ്ടതുണ്ട്. അതിനാൽ, ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്ന ഒരു പ്രത്യേക ചിത്രം ഞങ്ങൾ വരച്ചു. 7. യൂണിറ്റ് സർക്കിളിൽ ആവശ്യമുള്ള പ്രദേശങ്ങൾ ഹൈലൈറ്റ് ചെയ്യാൻ ഇത് സഹായിക്കുന്നു. അവ "+" അടയാളം കൊണ്ട് അടയാളപ്പെടുത്തിയിരിക്കുന്നു.
,
, ,
,
സൈൻ, കോസൈൻ ഫംഗ്ഷനുകളുടെ ഗുണവിശേഷതകൾ ഉപയോഗിച്ച്;
, എങ്കിൽ, എങ്കിൽ 
തുല്യം: 
, എങ്കിൽ:
,
b) 
,
വി) 
, 
, 
, 
.
.
പ്രിപ്പറേറ്ററി ഘട്ടത്തിൽ നേടിയ അറിവും നൈപുണ്യവും ഉപയോഗിച്ച്, വിദ്യാർത്ഥികൾ നിർദ്ദിഷ്ട അസമത്വം ഫോമിലേക്ക് കൊണ്ടുവരും. 
, എന്നാൽ ഫലമായുണ്ടാകുന്ന അസമത്വത്തിന് ഒരു കൂട്ടം പരിഹാരങ്ങൾ കണ്ടെത്തുന്നത് ബുദ്ധിമുട്ടാണ്, കാരണം സൈൻ ഫംഗ്ഷന്റെ ഗുണവിശേഷതകൾ ഉപയോഗിച്ച് മാത്രം ഇത് പരിഹരിക്കുക അസാധ്യമാണ്. ഉചിതമായ ചിത്രീകരണത്തിലേക്ക് തിരിയുന്നതിലൂടെ ഈ ബുദ്ധിമുട്ട് ഒഴിവാക്കാം (സമവാക്യം ഗ്രാഫിക്കായി പരിഹരിക്കുക അല്ലെങ്കിൽ ഒരു യൂണിറ്റ് സർക്കിൾ ഉപയോഗിക്കുക)..
x-അക്ഷത്തിന് സമാന്തരമായി അതിലൂടെ ഒരു നേർരേഖ വരയ്ക്കുക. ഈ രേഖ യൂണിറ്റ് സർക്കിളിനെ രണ്ട് പോയിന്റുകളിൽ വിഭജിക്കും. ഈ പോയിന്റുകൾ ഓരോന്നും സൈൻ തുല്യമായ സംഖ്യകളെ പ്രതിനിധീകരിക്കുന്നു .
. സ്വാഭാവികമായും, വരച്ച നേർരേഖയ്ക്ക് മുകളിലാണ് ഈ ആർക്ക് സ്ഥിതി ചെയ്യുന്നത്.
.
.
അസമത്വം സത്യമായ സംഖ്യകളെ തൃപ്തിപ്പെടുത്തുക 
. സൈൻ ഫംഗ്ഷന്റെ അതേ കാലയളവിൽ സ്ഥിതി ചെയ്യുന്ന സംഖ്യകളുടെ അസമത്വം ഞങ്ങൾ പരിഹരിച്ചു. അതിനാൽ, അസമത്വത്തിനുള്ള എല്ലാ പരിഹാരങ്ങളും ഫോമിൽ എഴുതാം 
രൂപത്തിൽ എഴുതാം 
, 
.
ഒപ്പം 
, അത് നൽകി 
.
അവന്റെ തീരുമാനവും 
, 
, 
, ഫോർമുലകൾ ഉപയോഗിച്ച് കണ്ടെത്തി 
, 
, 
.
ഗ്രാഫുകളുടെ ഇന്റർസെക്ഷൻ പോയിന്റുകളുടെ തുടർച്ചയായ മൂന്ന് അബ്സിസ്സസുകളാണ് ഒപ്പം . വ്യക്തമായും, എല്ലായ്പ്പോഴും ഇടവേളയിൽ 
അസമത്വം നിലനിർത്തുന്നു 
, ഒപ്പം ഇടവേളയിലും 
- അസമത്വം 
. ആദ്യ കേസിൽ ഞങ്ങൾക്ക് താൽപ്പര്യമുണ്ട്, തുടർന്ന് ഈ ഇടവേളയുടെ അറ്റത്ത് സൈനിന്റെ കാലഘട്ടത്തിന്റെ ഗുണിതമായ ഒരു സംഖ്യ ചേർത്താൽ, അസമത്വത്തിന് ഒരു പരിഹാരം നമുക്ക് ലഭിക്കും. ഇങ്ങനെ: 
, .
, നിങ്ങൾ അനുബന്ധ സമവാക്യം സൃഷ്ടിച്ച് അത് പരിഹരിക്കേണ്ടതുണ്ട്. തത്ഫലമായുണ്ടാകുന്ന ഫോർമുലയിൽ നിന്ന് വേരുകൾ കണ്ടെത്തുക 
ഒപ്പം 
, കൂടാതെ അസമത്വത്തിനുള്ള ഉത്തരം ഫോമിൽ എഴുതുക: , .
, അവസ്ഥ തൃപ്തിപ്പെടുത്തുന്നു 
;
, അവസ്ഥ തൃപ്തിപ്പെടുത്തുന്നു 
.
;
;
.
;
.
;
;
;
;
, എവിടെപി
(
x
)
ഒപ്പംക്യു
(
x
)
- യുക്തിസഹമായ അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിന് സമാനമായ യുക്തിസഹമായ ത്രികോണമിതി പ്രവർത്തനങ്ങൾ (സൈനുകൾ, കോസൈനുകൾ, ടാൻജന്റുകൾ, കോട്ടാൻജെന്റുകൾ എന്നിവ യുക്തിസഹമായി അവയിൽ ഉൾപ്പെടുത്തിയിട്ടുണ്ട്). നമ്പർ ലൈനിലെ ഇടവേളകളുടെ രീതി ഉപയോഗിച്ച് യുക്തിസഹമായ അസമത്വങ്ങൾ പരിഹരിക്കുന്നത് സൗകര്യപ്രദമാണ്. യുക്തിസഹമായ ത്രികോണമിതി അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള അതിന്റെ അനലോഗ് ത്രികോണമിതി സർക്കിളിലെ സെക്ടറുകളുടെ രീതിയാണ്.sinx
ഒപ്പംcosx
(
) അല്ലെങ്കിൽ ത്രികോണമിതി അർദ്ധവൃത്തംtgx
ഒപ്പംctgx
(
).
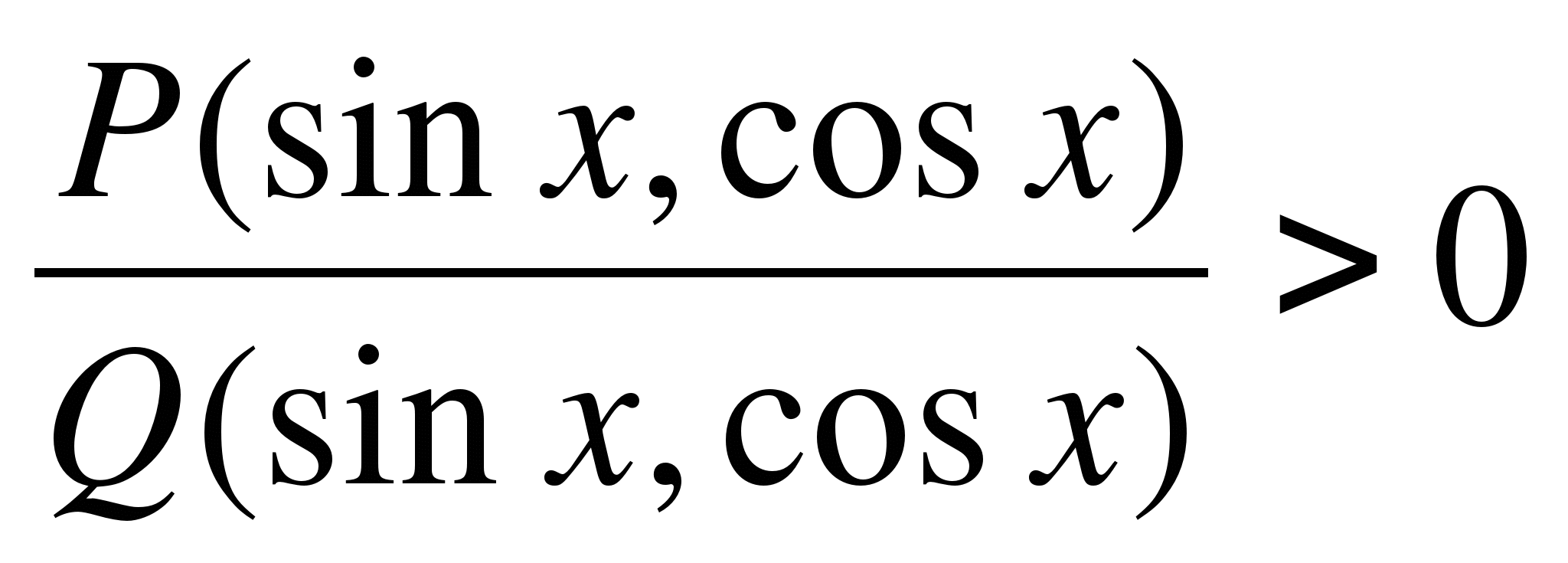
സംഖ്യാ അക്ഷത്തിൽ ഒരു ബിന്ദുവിനോട് യോജിക്കുന്നു 
, ഈ പോയിന്റിലൂടെ കടന്നുപോകുമ്പോൾ മാറ്റങ്ങളുടെ അടയാളം. സെക്ടർ രീതിയിൽ, ഫോമിന്റെ ഓരോ ഘടകങ്ങളും 
, എവിടെ 
- പ്രവർത്തനങ്ങളിൽ ഒന്ന്sinx
അഥവാcosx
ഒപ്പം 
, ഒരു ത്രികോണമിതി വൃത്തത്തിൽ രണ്ട് കോണുകൾ ഉണ്ട് 
ഒപ്പം 
, ഇത് സർക്കിളിനെ രണ്ട് സെക്ടറുകളായി വിഭജിക്കുന്നു. കടന്നുപോകുമ്പോൾ ഒപ്പം പ്രവർത്തനം മാറ്റങ്ങളുടെ അടയാളം.
ഒപ്പം 
, എവിടെ 
, എല്ലാ മൂല്യങ്ങൾക്കും അടയാളം നിലനിർത്തുക 
. ന്യൂമറേറ്ററിന്റെയും ഡിനോമിനേറ്ററിന്റെയും അത്തരം ഘടകങ്ങൾ മാറ്റുന്നതിലൂടെ ഉപേക്ഷിക്കപ്പെടുന്നു (എങ്കിൽ 
) അത്തരം ഓരോ നിരസിക്കലിലും, അസമത്വ ചിഹ്നം വിപരീതമാണ്.
ഒപ്പം 
ഉപേക്ഷിക്കപ്പെടുകയും ചെയ്യുന്നു. മാത്രമല്ല, ഇവ ഡിനോമിനേറ്ററിന്റെ ഘടകങ്ങളാണെങ്കിൽ, രൂപത്തിന്റെ അസമത്വങ്ങൾ അസമത്വങ്ങളുടെ തുല്യമായ സിസ്റ്റത്തിലേക്ക് ചേർക്കുന്നു. 
ഒപ്പം 
. ഇവ ന്യൂമറേറ്ററിന്റെ ഘടകങ്ങളാണെങ്കിൽ, തുല്യമായ നിയന്ത്രണ സംവിധാനത്തിൽ അവ അസമത്വങ്ങളുമായി പൊരുത്തപ്പെടുന്നു. ഒപ്പം കർശനമായ പ്രാരംഭ അസമത്വത്തിന്റെയും സമത്വത്തിന്റെയും കാര്യത്തിൽ 
ഒപ്പം 
കർശനമല്ലാത്ത പ്രാരംഭ അസമത്വത്തിന്റെ കാര്യത്തിൽ. ഗുണിതം നിരസിക്കുമ്പോൾ 
അഥവാ 
അസമത്വ ചിഹ്നം വിപരീതമാണ്.
, b) 
.
ഞങ്ങൾക്ക് ഫംഗ്ഷൻ ഉണ്ട് b) . നമുക്കുള്ള അസമത്വം പരിഹരിക്കുക,
, 
.
